基于信噪比与综合赋权的涤纶低弹丝工艺优化模型

邵景峰，李 宁, 蔡再生

(1.西安工程大学 管理学院，陕西 西安 710048；2.东华大学 化学化工与生物工程学院，上海 201620)

我国是纺织大国，在众多纺织产品中，涤纶低弹丝(draw texturing yarn, DTY)因具有断裂强度和弹性模量高以及耐热耐光等优良特性成为针织、机织加工的理想原料。然而，由于涤纶低弹丝组成成分复杂，加工过程中工艺参数难以获取，多项工艺参数(如加工速度、热箱温度等)之间存在耦合制约关系，并且生产过程能耗高，因此难以合理建模和优化涤纶低弹丝生产过程中的能耗、工艺参数以及质量指标之间的相关关系。如何构建涤纶低弹丝生产过程的关键工艺参数优化模型，在提高纤维质量的基础上降低生产过程能耗的问题亟待解决。

国外学者通过借助生命周期评价(life cycle assessment, LCA)和能耗测量技术对差别化纤维优化进行了研究。例如：Muthu等[1]通过建立碳足迹模型，验证纺织材料的循环利用是减少纺织过程链中碳足迹的有效途径之一；van der Velden等[2]对棉、涤纶等纤维织物构建了详细的LCA基准，分析得出了环境负荷与生产过程之间的关系；Khayyam等[3]提出一种基于混合整数线性规划方法的随机优化模型，实现了给定范围内碳纤维生产质量的预测；Raileanu等[4]提出一种基于Agent的车间制造过程资源能耗实时测量的控制框架，通过作业调度来优化整个车间制造过程中的能耗；Karthik等[5]针对牛仔布生产工艺流程，应用LCA对整个工艺流程进行了碳足迹核算与分析。同时，国外学者们还将研究聚焦于智能优化理论与方法的应用方面。例如：Fallahpour等[6]提出一种新的多指标决策技术优化转杯纺并条机参数，并采用模糊多属性决策方法对优化参数进行了评价；Deilamani等[7]借助响应面法优化涤纶主要加捻变形参数，提升涤纶微丝拉伸性能，提高结晶度；Song等[8]提出一种基于自校正比例积分导数的温度控制方法，有效提高了DTY热箱温度的控制精度；Stojanovic等[9]从结晶度、取向度和卷曲性能等方面对变形纱进行研究，分析假捻变形参数对涤纶纱线结构和卷曲性能的影响。

我国学者将研究点集中于差别化纤维的具体生产实践，探讨工艺的最优参数。例如：赵年花等[10]根据PAS 2050规范，应用LCA软件对涤纶长丝织物从原油开采到完成印染加工的整个过程进行碳足迹核算，得出蒸汽和电力是低碳控制的两个关键生产要素；王来力等[11]在构建纺织服装行业能源消费碳排放因素分解模型的基础上，对影响因素进行了实证分析；刘笑莹等[12]通过设备改造和试验获得优化工艺方案，降低棉/大麻混纺工艺过程中的大麻损耗，为提高纱线品质提供了新思路。随着智能化生产的不断完善，基于数据驱动的工艺参数优化研究逐渐展开。例如：徐楠等[13]提出一种改进第二代非支配排序遗传算法，对涤纶长丝熔体输送过程进行了工艺参数优化；刘琼等[14]提出一种产品制造过程碳足迹计算方法，构建多目标优化调度模型，并设计第二代非支配解遗传算法对调度模型进行求解，减少了产品制造过程中的碳足迹；顾敏明等[15]构建一种涤纶织物热定型过程参数优化方法，运用粒子群算法对温度参数进行寻优，降低了生产过程能耗。

综上可知，国内外学者对于差别化纤维碳足迹的研究大都停留在核算过程上，很少给出降低碳排放的具体方法，针对涤纶生产实践的研究主要通过优化建模以实现对工艺参数的寻优，但缺乏对降低能耗的相关考虑。因此，在考虑绿色低碳生产的基础上，本文基于数据驱动与碳足迹理论，构建一种涤纶低弹丝生产关键工艺参数优化模型，以实现降低生产能耗的同时提高纤维质量的目标。

1 构建能耗分析模型

学者们将碳足迹作为量化产品生命周期中能耗分析的理论依据。Chen等[16]提出一种多约束计算模型，进一步提高碳排放评价的准确性，为服装柔性制造的碳工艺评价提供新思路；俞璐等[17]对服装生产线进行分析，分阶段建立碳排放计算模型，为量化研究提供计算参考。基于此，本文围绕涤纶低弹丝生产工艺流程，应用碳足迹理论分析涤纶低弹丝生产过程中的投入与产出，构建涤纶低弹丝生产过程的能耗分析模型，如图1所示。

由图1可知，针对每个涤纶低弹丝生产工艺流程,可建立涤纶低弹丝生产过程的碳排放指示量Cx，如式(1)所示。

(1)

式中：Wij为DTY生产过程中的第i类能源转化的第j个碳消耗量，kg(以1 kgCO2的碳含量为标准计量单位)；fi为第i类能源消耗对应的碳排放系数。

2 能耗分析与碳足迹核算

由图1可知，DTY的加弹生产工艺流程具体表现：POY(pre-oriented yarn)原丝在第一热箱进行变形拉伸处理，在导入假捻器之前，需将温度较高的丝条先行冷却，冷却后的丝条进入第二热箱进行加热定型，并通过上油处理以提高纤维的抗静电性，最后，经过卷绕、检测等工序生产出合格DTY。因此，对DTY加弹工艺流程进行分解，分别核算碳排放。

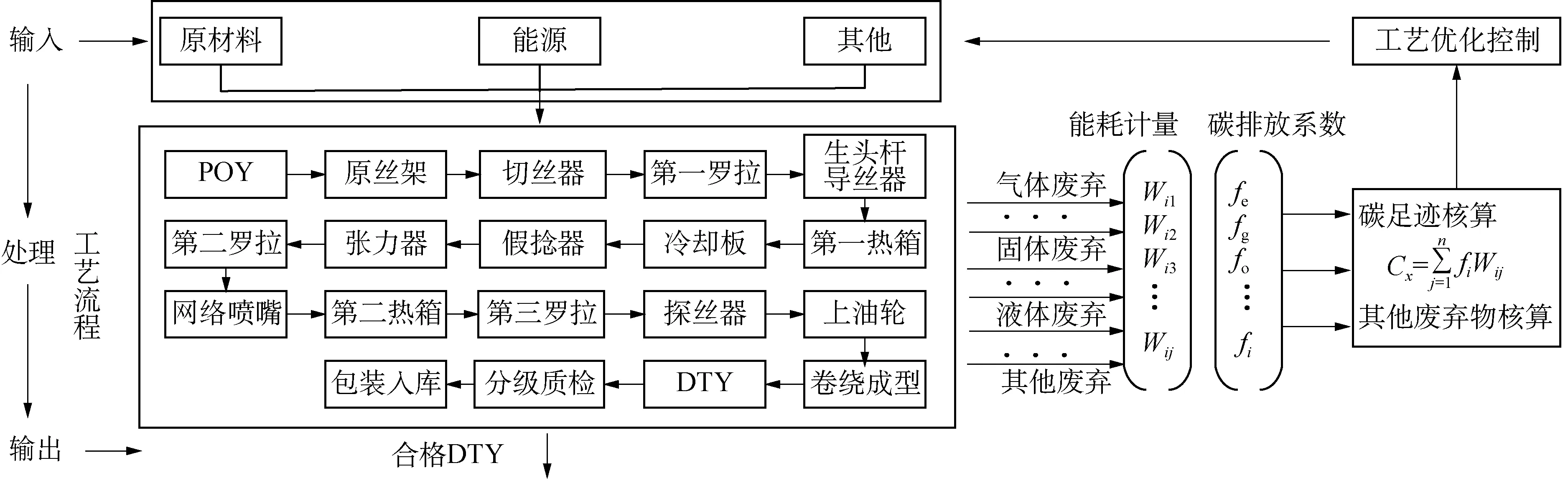
图1 涤纶低弹丝生产过程的能耗分析模型Fig.1 Energy consumption analysis model of draw texturing yarn process

通过真空联苯蒸汽加热以及电加热复合的方式，在第一热箱中对丝条进行变形拉伸操作，其中，第一罗拉(l1)传动的电能消耗Wl1、排烟系统(m2)的电能消耗Wm2、电加热丝(h1)的电能消耗Wh1、电动机(m1)的电能消耗Wm1是主要的能源碳排放，油剂废气排放量Wn1(以非甲烷总烃计量)是丝条在加热过程中主要的工艺碳排放。基于此，此阶段碳足迹核算如式(2)所示。

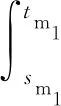
(2)

式中：fe为电能对应的碳排放系数；积分下限s和上限t分别代表设备开启和停转的时间，h；P为各设备部件运转时的实际功率，kW；rh1为电加热丝的条数；Th1为电加热丝的加热时长，h；fg为油剂废气对应的碳排放系数；λ为以油剂废气排放占比；k为油剂含量，以每吨POY丝的体积为单位，m3/t；Gpoy为POY丝的单位消耗量，t。

丝条经过变形拉伸后还处于温度较高的状态，为使它的变形固定下来后具有足够的刚性，需将丝条通过金属板空气冷却至低于80 ℃，并改善通风条件，调节室内温度，控制丝条假捻温度和假捻张力，保证丝条变形的均匀性及在假捻过程中的捻度传递。此阶段碳排放主要为能源碳排放，包括空气压缩机(m3)的电能消耗Wm3、引风机(m4)的电能消耗Wm4以及龙带传动的假捻系统(m5)的电能消耗Wm5。基于此，此阶段碳足迹核算如式(3)所示。

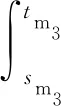
(3)

在此基础上，利用第二热箱对丝条进行补充热定型，以提高丝条卷曲稳定性并消除丝条纤维结构中的内应力。非接触式联苯蒸汽加热为此过程中的主要加热方式，其中，电加热丝(h2)与第二罗拉(l2)传动两部分的电能消耗Wh2、Wl2为能源碳排放的主要指标，油剂废气排放量Wn2是丝条在加热过程中主要的工艺碳排放。基于此，此阶段碳足迹核算如式(4)所示。

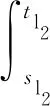
(4)

静电效应及僵死现象通常产生在卷绕、落丝过程中，因此在卷绕和落丝操作前需对丝条进行上油处理，从而改善纤维的抗静电性和降低断头率，以适应后道工序的要求。因此碳排放具体表现为第三罗拉(l3)传动的电能消耗Wl3与DTY油剂(o)的消耗量Wo。基于此，此阶段碳足迹核算如式(5)所示。

(5)

式中：fo为DTY油剂对应的碳排放系数；no为上油轮转速，r/min；co为单位轮转的油剂消耗量，L；to为上油时长，h。

上油处理后DTY丝的抱合力和强度都得到了提高，压在摩擦辊上的丝层随摩擦辊转动而卷绕在丝筒上，从而完成卷绕和落丝操作。因此碳排放具体表现为电动机(m6)卷绕时的电能消耗Wm6、摩擦辊(m7)传动的电能消耗Wm7以及丝条落丝电动机(m8)的电能消耗Wm8。基于此，此阶段碳足迹核算如式(6)所示。

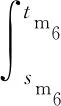
(6)

综上，将Cx(x=1,2,3,4,5)代入式(1)整理，可得整个过程的碳排放量Ce，如式(7)所示。

(7)

式中：Whi为第i个设备电加热丝的电能消耗，kW·h；Wmi为第i个设备器件的电能消耗，kW·h；Wli为第i罗拉转动的电能消耗，kW·h；Wni为第i个油剂废气排放量，m3。

3 构建关键工艺参数优化模型

3.1 拟合涤纶低弹丝生产碳排放核算函数

涤纶低弹丝生产过程中能耗占比最大的是电能消耗，具体包括加弹机的变形拉伸、罗拉传动、排烟及卷绕成型装置的动力消耗，还有电辅热系统的电能消耗等[18]。在加弹工艺流程中，丝条在变形热箱内加热时间的长短，取决于加工速度的快慢，并且牵伸比的设定要保证DTY拥有良好的力学性能。同时，在DTY的上油工艺流程中，影响DTY油剂消耗的工艺参数主要有油轮转速、油尺高度、油针孔径等。在整个生产过程中也会产生相应的固态、液态、气态废弃物，如废丝、废水、废油以及废气等。

基于此可知，在DTY加弹工艺参数中，加工速度(vl2)、牵伸比(b)、第一热箱温度(th1)、第二热箱温度(th2)、油轮转速(no)和油尺高度(ho)均是与碳排放相关及影响DTY质量指标的关键工艺参数，因此，可构建碳排放指标与各关键工艺参数之间的函数关系。借助MATLAB R2018b分析软件，对涤纶低弹丝加弹过程中碳排放量与关键工艺参数的关系进行分析与优化，得到碳排放量Ce与油轮转速x1、加工速度x2、牵伸比x3、油尺高度x4、第一热箱温度x5、第二热箱温度x6之间的二次回归方程如式(8)所示。

C(x)=5.640 4x2-0.775 7x4+56.500 0x5-

0.316 6x2x3-0.062 3x1x4+0.000 5x2x4+

0.003 6x2x5-3.082 5x3x5-0.012 9x4x5-

1.539 5x3x6+0.006 9x4x6+0.461 1x5x6-

(8)

3.2 正交试验因子确定

在3.1节的基础上，选取关键工艺参数作为正交试验因子，其他参数设定为标准值，选取碳排放量(Ce)、断裂强度(Z1)、断裂伸长率(Z2)、卷曲收缩率(Z3)、沸水收缩率(Z4)、卷曲稳定度(Z5)以及含油率(Z6)作为综合优化指标，设计6因素5水平的正交试验L25(56)，如表1所示。

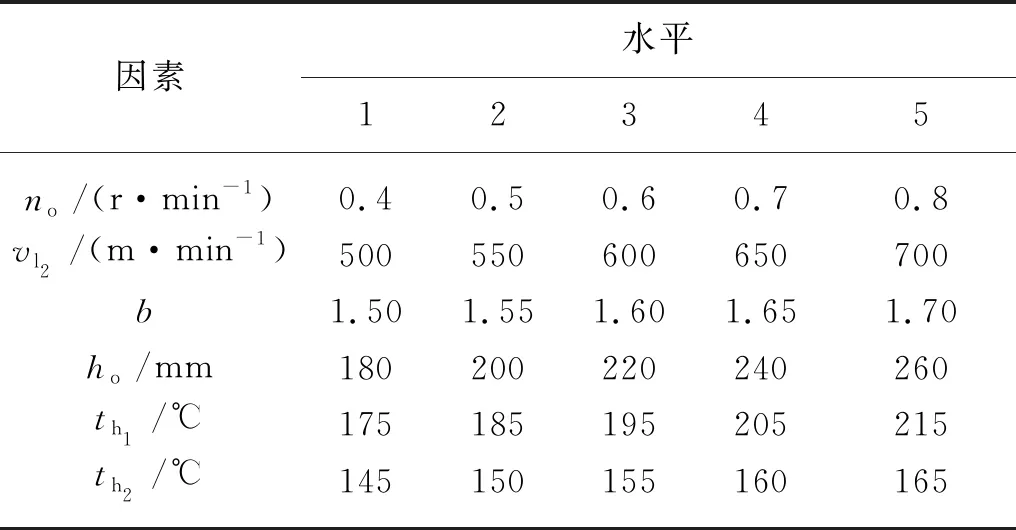
表1 正交试验设计方案

3.3 基于信噪比的正交试验

为评估产品质量指标的稳健性，通常用信噪比(signal-to-noise ratio, S/N)作为衡量产品质量特征值波动的指标[19]。因此，采用信噪比结合正交试验设计的方法，进一步评估DTY成品质量指标。对于不同要求的特征值，信噪比具有望大特征或望小特征。考虑到所选质量指标在一定范围内越大，DTY质量越好，因此，选择信噪比的望大特征如式(9)所示。

(9)

由于碳排放量越小越好，所以选择信噪比的望小特征如式(10)所示。

(10)

式中：aS/N为DTY指标的信噪比值；n为每组试验的重复次数；yi为第i次试验的DTY指标值。

根据表1中的试验因素及水平，通过正交表设计25组试验，得到每组试验对应的DTY断裂强度、断裂伸长率、卷曲收缩率、沸水收缩率、卷曲稳定度和含油率，并将试验结果代入式(9)中，将碳排放量代入式(10)中，分别得到相应的信噪比值。

3.4 基于VIKOR法的工艺参数优化

VIKOR法(vlsekriterijumska optimizacija i kompromisno resenje)是在TOPSIS法(technique for order preference by similarity to an ideal solution)基础上发展而来的一种最佳妥协解的多属性决策方法[20-23]，应用VIKOR法的决策思想，不但可以得到各关键工艺参数对综合优化指标的影响层次，而且可获取最终评价结果的优劣[20-23]。将信噪比引入正交试验设计，并结合综合赋权VIKOR法，实现DTY指标由复杂到单一的转化，其中，将每组试验视为一种决策方案，通过比较不同水平下每组试验距离最优理想解的程度，优选最佳决策方案。

3.4.1 数据预处理

由于碳排放量与质量指标之间量纲不同，在预处理阶段首先要对原始数据矩阵进行规范化处理，如式(11)和(12)所示。

(11)

(12)

式中：Xij为原始数据矩阵第i行第j列的数据；Yij为Xij经过规范化处理后的结果。

所选取的DTY质量指标(Z1,Z2,Z3,Z4,Z5,Z6)在一定范围内均为望大型指标，数据按照式(11)进行预处理，碳排放量(Ce)为望小型指标，数据按照式(12)进行预处理。试验数据规范化处理结果如表2所示。

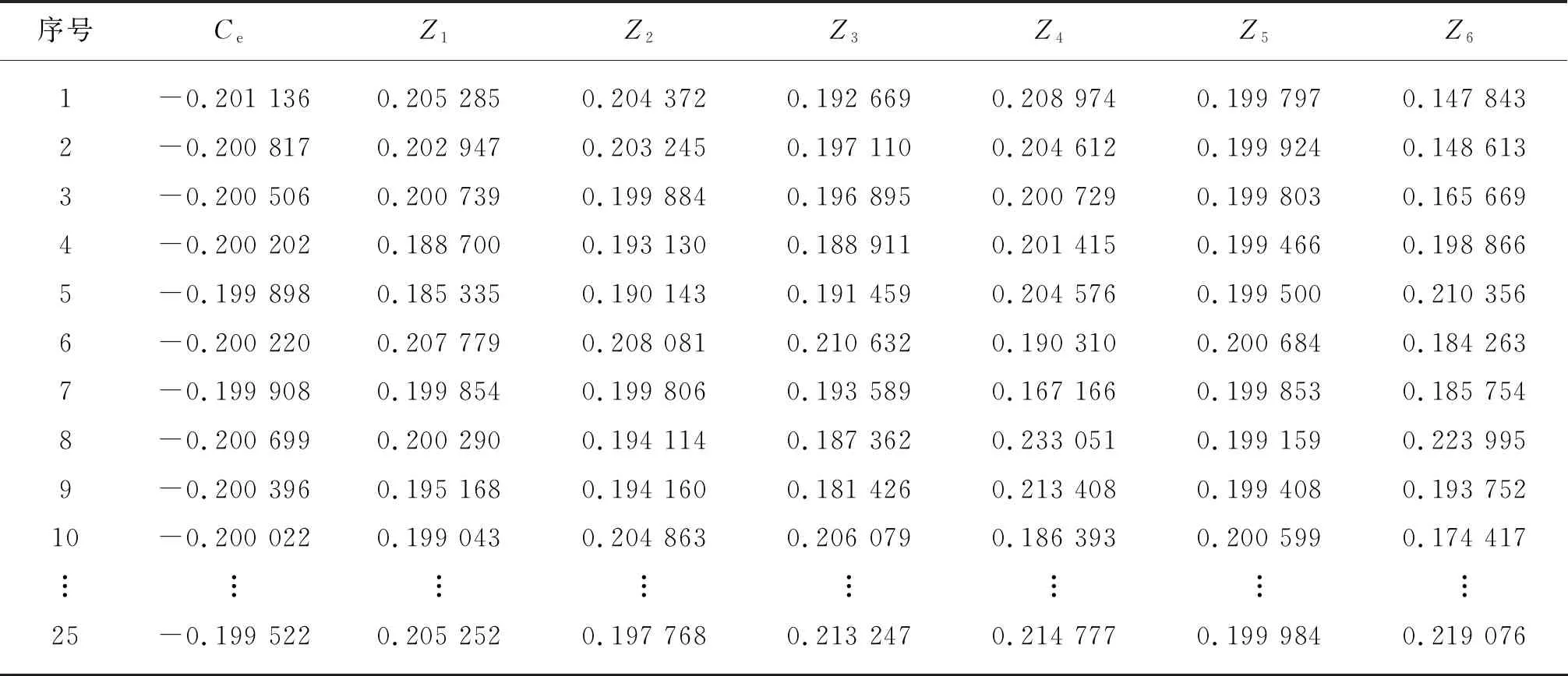
表2 试验数据规范化处理结果

3.4.2 DTY指标综合权重确定

(1) 熵值赋权法。熵的概念在模糊集相关领域被引入后，熵值赋权法被广泛应用于指标数据属性权重的确定[20]。第j个指标的熵值ej如式(13)所示。

(13)

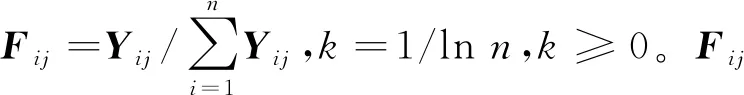
(2) CRITIC赋权法。CRITIC(criteria importance through intercrieria correlation)赋权法作为一种客观赋权法，以对比强度和指标间冲突性作为权重基础，其中，对比强度用标准差来表示，指标间冲突性用相关系数来体现，通过对原始数据进行充分的信息挖掘，进而对综合指标进行科学评判[22]。第j个信息值Cj如式(14)所示。

Cj=σjDj

(14)

(15)

式中：σj为第j个标准差；Rij为第i个与第j个指标之间的相关系数矩阵。

(3) 综合权重的确定。虽然CRITIC赋权法在客观赋权法中较为完善，但其在考虑数据间的离散性上存在不足，而熵值赋权法则可以对此进行弥补。因此，本文将熵值赋权法与CRITIC赋权法相结合进行综合赋权，从而充分挖掘数据间的关联。在综合权重的确定上，运用乘除法进行计算，第j个综合权重Kj如式(16)所示。

(16)

基于此，DTY指标的权参数及权重结果如表3所示。

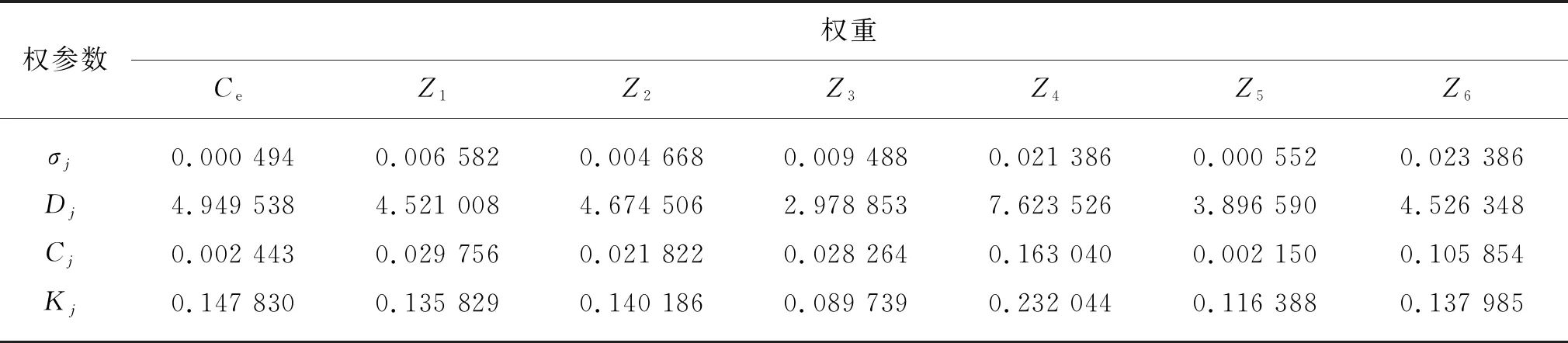
表3 DTY指标的权参数及权重

3.4.3 正、负理想解的确定

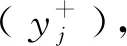
(17)

(18)

3.4.4 群体效益值确定

群体效益值的确定如式(19)所示。

(19)

式中：Bi为试验方案中第i个群体效益值，其值大小与群体效应相反；yij为规范化矩阵中第i行第j列的数据。

各试验方案的群体效益值如表4所示。

3.4.5 个体遗憾值确定

个体遗憾值的确定如式(20)所示。

(20)

式中：Pi为试验方案中第i个个体遗憾值，其值大小与个体遗憾值成正向关系。

各试验方案的个体遗憾值如表4所示。

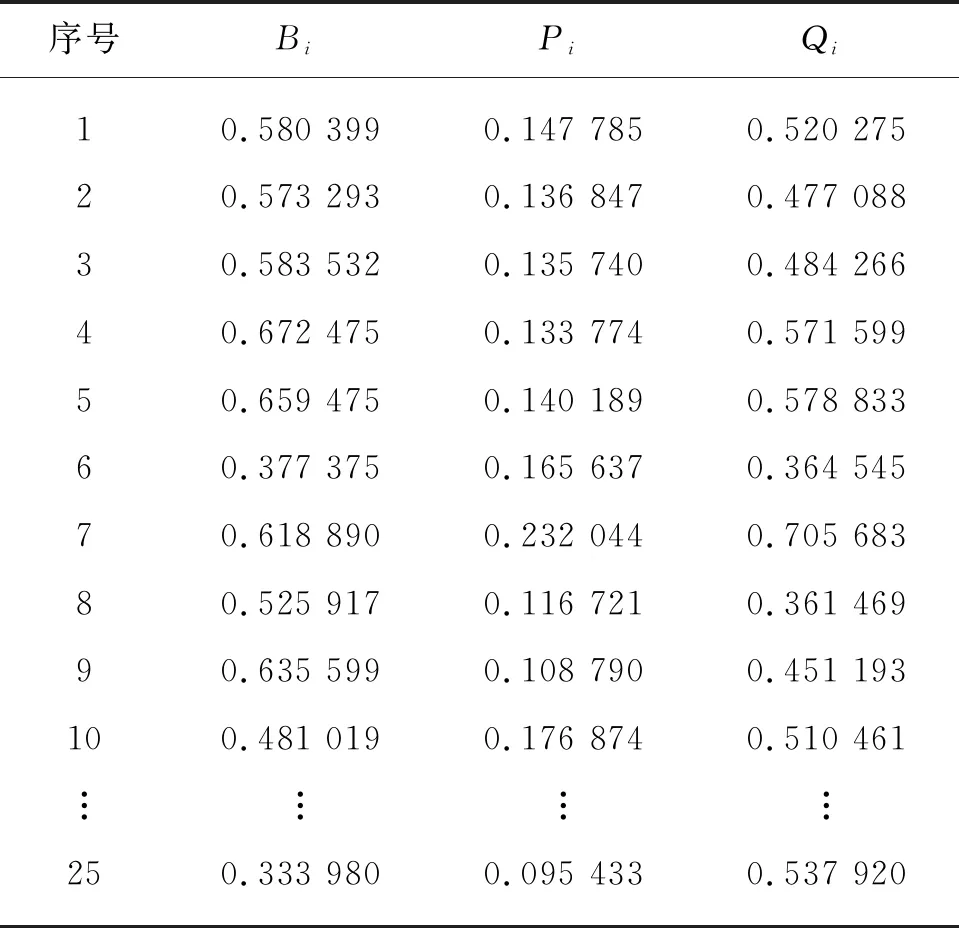
表4 各试验方案的Bi、Pi、Qi值

3.4.6 试验方案的利益比率确定

试验方案的利益比率确定如式(21)所示。

(21)

式中：Qi为试验方案中第i个利益比率；B+、B-分别为试验方案的最大、最小群体效益值；P+、P-分别为试验方案的最大、最小个体遗憾值；v为决策机制系数，其值大小代表决策者对Bi、Pi的偏好程度，因此为缩小Bi和Pi的影响程度，v取值0.5。

各试验方案的Qi值如表4所示。

应用综合赋权的VIKOR法优化DTY生产关键工艺参数，依据各工艺参数水平对应的平均Qi值的大小对试验方案进行评价，平均Qi值越小则越逼近正理想解，代表的工艺水平越优。基于此，5种工艺水平下DTY生产关键工艺参数的平均Qi值如表5所示。

表5 DTY生产关键工艺参数平均Qi值

由表5可知：对于油轮转速，Q3最小，因此水平3为最优工艺水平；对于加工速度，Q1最小，因此水平1为最优工艺水平；对于牵伸比，Q4最小，因此水平4为最优工艺水平；对于油尺高度，Q3最小，因此水平3为最优工艺水平；对于第一热箱温度，Q1最小，因此水平1为最优工艺水平；对于第二热箱温度，Q3最小，因此水平3为最优工艺水平。

综上可知，优化后的DTY生产关键工艺参数：油轮转速为0.6 r/min，加工速度为500 m/min，牵伸比为1.65，油尺高度为220 mm，第一热箱温度为175 ℃，第二热箱温度为155 ℃。

4 优化模型验证分析

在3.1节的基础上，借助MATLAB R2018b分析软件，实现碳排放量与关键工艺参数之间的二次回归方程拟合，拟合残差分布如图2所示。从图2可以看出，残差值正态分布概率逼近直线两侧，说明此二次回归方程具有良好的拟合性能。

图2 碳排放量与关键工艺参数拟合残差分布Fig.2 Residual distribution of carbon emission and key process parameters

现有初始工艺条件下的DTY生产关键工艺参数：油轮转速为0.4 r/min，加工速度为700 m/min，牵伸比为1.70，油尺高度为220 mm，第一热箱温度为205 ℃，第二热箱温度为160 ℃。将初始工艺条件下的DTY生产关键工艺参数代入式(8)中，得到涤纶低弹丝加弹生产过程中的初始碳排放量为200.73 kg，同时将优化后的DTY生产关键工艺参数代入式(8)中，得到优化后的碳排放量为182.53 kg， 与初始碳排放量相比，下降了9.06%。通过试验平台检验，在优化后的工艺条件下，所生产出的DTY平均断裂强度、断裂伸长率以及卷缩性等质量指标均有所提高，纤维不易产生断头与毛丝，具有更加良好的蓬松性。但其平均沸水收缩率有所下降，可能因为加工速度的降低，导致丝条在第二热箱中的热定型时间缩短，纤维内应力松弛程度增大，丝条在沸水中的应力松弛减小，因此沸水收缩率减小。DTY指标在关键工艺参数优化前后对比值如表6所示。

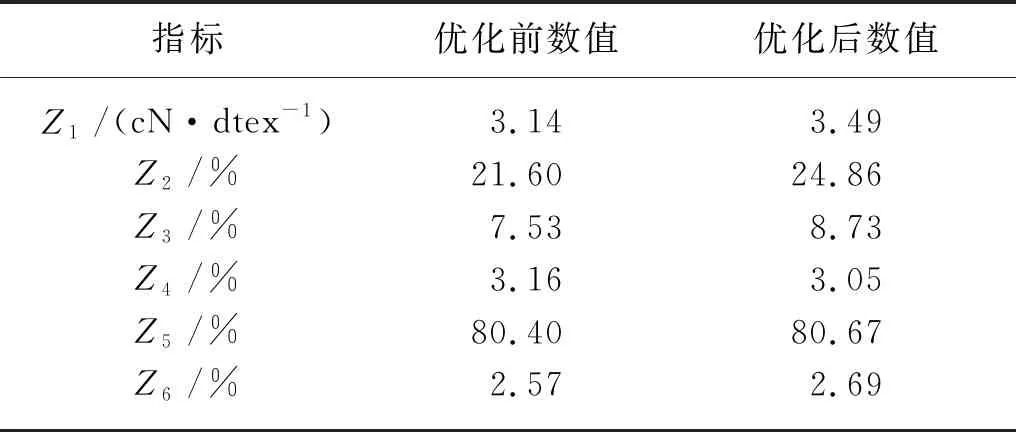
表6 DTY指标在关键工艺参数优化前后对比值

5 结 语

本文应用碳足迹理论对涤纶低弹丝生产各阶段进行了碳足迹核算，并构建碳排放量与关键工艺参数之间的核算函数，借助MATLAB R2018b分析软件，基于核算函数构建信噪比正交试验与综合赋权VIKOR法相结合的关键工艺参数优化模型，并进行模型求解。由分析与验证结果可知，所构建的优化模型可以实现对关键工艺参数的优化，当关键工艺参数组合为油轮转速0.6 r/min、加工速度500 m/min、 牵伸比1.65、油尺高220 mm、第一热箱温度175 ℃、第二热箱温度155 ℃时，可降低DTY加弹生产过程中的碳排放量，同时提高DTY成品质量指标，生产出具有良好品质的涤纶低弹丝。