有轨电车路基板-疏桩基础长期沉降现场实测与数值分析
徐正良,刘 磊,王浩然,俞 剑,黄茂松
(1.上海市城市建设设计研究总院(集团)有限公司,上海200125;2.同济大学地下建筑与工程系,上海200092;3.同济大学岩土及地下工程教育部重点实验室,上海200092)
现代有轨电车采用新型车辆,拥有更高路权和良好景观效果,在补充城市轨道交通布局、提升地面公共交通品质方面起了积极作用。作为“绿色”交通工具,现代有轨电车以其安全、节能、环保、建设周期短、投资相对节省的优势,在我国得到了广泛应用,有着广阔的发展空间和前景[1]。截止2018年底,有近30条线路开通运营,20多个省份的超过90座城市规划了有轨电车,规划线路超过10 000 km。有轨电车迎来发展机遇的同时也对轨下基础(包括路基工程)提出了更高的技术要求。
有轨电车正线一般采用无砟道床结构,对工后沉降要求严格,上海市《有轨电车工程设计规范》什(DG/TJ08-2213—2016)[2]规定有轨电车无砟轨道路基工后沉降不应超过50 mm,工后不均匀沉降量不应超过扣件允许可调量。因此在软土地基上修建有轨电车时应进行充分研究,采取合理措施以防止过大沉降。结合有轨电车工程特点,软土地区控制路基沉降技术主要有:换填法、复合地基法、桩筏结构法、真空预压[3]、真空预压联合搅拌桩[4]等。尽管这些基础形式应用较广,但工后长期沉降控制仍无法满足有轨电车运营要求。
于是,路基板-疏桩方案应运而生,这种新型路基是在轨道路基分离式桩板结构的基础上优化而成。可用于路桥过渡段对差异沉降要求严格或深厚软土沉降不宜控制的路段。轨道采用短轨枕,埋入路基板中,一次浇筑完成,可减少混凝土和钢筋用量。一体化轨下基础在路基板结构钢筋外侧单设排流网,耐久性好,减少杂散电流对周边管线影响。基础结构可采用预制桩或灌注桩,以调平工后沉降为主,并辅以板底地基土支承作用。
对于交通荷载下的路基长期沉降问题,目前主要集中在无砟道床结构,如叶斌等[5]利用有限元动态分析方法研究了粉土路基在交通循环荷载作用下的动态响应,吕玺琳等[6]探究了软土路基在循环交通荷载下的长期沉降理论解,Chai等[7]提出了一种低路堤软土地基上交通荷载引起的道路沉降预测方法,崔新壮等[8]通过对现场土进行交通荷载模拟试验,提出一种基于原位测试技术得到土体累积变形公式进而计算路基长期沉降的方法。而减沉疏桩基础主要应用于建筑地基,其沉降的计算方法大多依据规范方法,计算出承台下地基土分担荷载产生的沉降和桩受荷后引起的桩间土的变形,结合沉降计算经验系数获得最终沉降。徐奋强等[9]提出了软土地基符合疏桩基础沉降计算的改进联合法;孙晓东[10]将减沉复合疏桩基础应用在非软土地区;方成等[11]利用两个实际工程案例对规范提出的减沉疏桩沉降计算方法的可靠度加以验证。显然,现有研究主要基于减沉疏桩基础在静力荷载作用下的沉降分析,尚无针对路基板-疏桩基础在有轨电车长期循环荷载作用下沉降累积的研究。
对于路基板-疏桩此类复杂基础形式通常较难形成有效的简化分析方法,弹塑性有限元分析方法对此具有独特的优势,但依托复杂的弹塑性循环本构开展数十万次的长期循环计算,时间成本是难以接受的。为避免复杂的循环本构模型计算,同时尽可能反映循环荷载的影响,可考虑将土体经验模型应用到数值计算中,这类方法主要包括有等效刚度法(如Achmus等[12]、张勋[13]、朱治齐[14])和等效有限元方法(如Wichtmann[15]、Pasten等[16])。等效刚度法是基于土体刚度随荷载循环次数增加而逐渐变化的思路,通过改变土体模量以模拟循环荷载作用下土体累积变形特性。等效有限元方法在计算过程中借鉴了初应变方法的概念,在计算中改变应变而非模量。魏星等[17]及马霄等[18]借鉴了初应变法的理念,采用等效有限元方法分析了交通荷载作用下软土地基的长期沉降,在有轨电车软土路基分析中的应用尚处于空白。上述学者研究发现,当循环次数较小时,两种方法计算结果较为接近,而当循环次数较大时,等效有限元的计算结果更加接近实际值。
综上所述,本文研究对象“路基板-疏桩”结构在长期循环荷载下的沉降分析需考虑土体、路基板、基桩三者的位移协调,相较于一般桩筏基础静力沉降问题更加复杂,而目前简化理论方法仅能处理这类基础的静力承载特性问题,而传统弹塑性有限元也无法胜任超大循环数目下的道基沉降分析。等效有限元方法可以克服传统有限元本构复杂、计算效率低等缺点,能够有效解决基础结构复杂并在长期循环荷载作用下的沉降问题。本文依托南方某有轨电车项目,首先对路基板-疏桩基础开展了为期长达两年的沉降监测以了解减沉效果并掌握其沉降特性,并实现了长期交通荷载作用下路基板-疏桩基础一体化沉降等效有限元分析方法,与现场长期监测结果对比,验证了该方法的合理性。并基于该项目进一步对比了路基板-疏桩基础和无砟道床结构的减沉效果,同时也探讨了疏桩长度对沉降控制的影响,为后续深厚软土层有轨电车路基设计计算提供参考。
1 有轨电车路基长期沉降监测
南方某轨道交通延伸线工程,西起二号地块,串联二号地块、三号地块、四号地块(线路见图1a),起点里程(二号地块)XDK0+055.000,终点里程XDK1+737.084(三、四号地块),全长1 682.084 m。线路最高设计时速70 km·h-1。土层分布自上而下依次为①素填土、③1粉质黏土、③2淤泥质土、④2砂质粘性土以及⑤2全风化花岗岩,因地表软土层比较深厚,故全线采用路基板-疏桩方案(图1b)。预应力混凝土管桩,桩径0.5 m,桩纵向间距3.8 m,横向间距2.0 m;路基单行线宽4.0 m,桥梁及特殊路段为钢筋混凝土现浇U型槽,普通路段为0.3 m的支承层(C25素混凝土)和0.4 m的基床表层(水稳碎石),如图2所示。
沉降监测点在路基沿线等间隔布置,一般路基段每100 m布设1个观测断面,沉降点位于路基中部位置,路基填筑前,于路基基底地面埋设沉降板进行监测,每个监测断面设置1个沉降板。依据沉降观测点的埋设要求或图纸设计的沉降观测点布点图,确定沉降观测点的位置。在控制点与沉降观测点之间建立固定的观测路线,并在架设仪器站点与转点处作好标记桩,保证各次观测均沿统一路线。为保证沉降观测的可靠性,保证基准点稳定可靠,每3个月对基准网进行定期复测。测点大样与现场测点图见图2。监测历时约两年时间,自2017年8月到2019年5月底。

图1 项目路线与路基板-疏桩基础Fig.1 Project route and track bed with sparse pile foundation

图2沉降观测点大样图和沉降测点实图(单位:mm)Fig.2 Map of large sample view of settlement observation point and settlement measurement point(unit:mm)
图3显示了D089和D206两测点(测点位置见图1)的沉降规律,在运行初期,土体沉降发展迅速,地表位移明显增加,约一年后沉降速率放缓,并于两年左右趋于稳定。2019年5月底最后一次监测数据显示,D206为全线最大累积沉降点,约16 mm,满足规范中绝对沉降不大于50 mm的控制要求。此外,该项目要求一般路段不均匀沉降变形允许值每20 m为20 mm。鉴于最大沉降点D206的绝对沉降小于20 mm,且已基本趋于稳定,故可推断一般路段的差异沉降值满足要求。说明路基板-疏桩基础可有效将有轨电车荷载传递至深层地基中共同分担荷载,减少浅层软土承受的附加应力。
图4显示了测点D089和D206的土层分布,值得注意的是相较测点D089,测点D206的⑤2全风化花岗岩层埋深更浅,但其沉降却比D089大约80%,这可能是由于测点D206所在处有厚达9 m的高压缩性淤泥质土层(③2)所导致,而测点D089处淤泥质土层厚度仅有2 m。两测点间的沉降差异将在后文有限元分析中进一步展开讨论。

图3 D089和D206监测点实际沉降值Fig.3 Monitored settlements at D089 and D206

图4 D089和D206测点土层分布图Fig.4 Distribution map of soil layer of D089 and D206
2 等效有限元方法
2.1 等效有限元方法的建立
传统弹塑性有限元在模拟土体循环累积变形特性时要采用复杂的土体循环本构模型,计算效率较低,且收敛性差,在模拟超大数目循环荷载时,需耗费极大的时间与计算成本。本文借鉴初应变方法的思路(图5)以解决上述问题,初应变法先是根据施加于土体上的真实应力σtrue和弹性参数(弹性模量E)计算得到试算应变εtrial,再将εtrial与真实应变εtrue之间的差值作为初应变εinitial,通过迭代等方法获取该初应变后即可获得εtrue。本文将基于显式模型[19]得到的土体累积应变视作初应变,从而建立可模拟长期循环累积变形的等效有限元计算方法。显式模型与一般的本构模型都是描述材料在外力作用下的变形特性,不同的是显式模型中出于简化计算的需要没有直接建立应力-应变关系,而是建立加载次数与应变的关系,故不能直接用于有限元计算。

图5 初始应变方法示意图Fig.5 Schematic diagram of initial strain method
本文通过等效有限元法建立了在显式模型的基础上获得考虑边界影响和单元应变协调的三维有限元分析方法。基于ABAQUS有限元软件,进行二次开发,实现了自单元应变得到节点位移的有限元计算过程。将由经验模型得到的单元应变作为初应变分析,此时应力应变关系可表示为

式中:σ为应力张量;De为假设的弹性刚度系数张量;ε为应变张量;εa为初应变张量。由式(1)可通过最小位能原理得到对应的有限元方程:

式中:K为总刚度矩阵;u为节点位移向量;F为节点荷载向量;FT、Ff和Fε0分别为体积荷载项、表面荷载项和初应变引起的荷载向量。初应变εa会在单元应力引起对应的应力σ0,在有限元方程中反映为虚拟节点荷载Fε0。此时计算得到的应变和位移满足边界条件和变形协调条件的影响。但计算得到的应力是虚拟的,并非实际的应力状态。
通过假设弹性矩阵De,可得到初应变εa对应的初应力σ0与初应变引起的等效节点荷载向量Fε0:

其中,B为由单元节点位移计算应变的矩阵,由形函数决定。需要指出的是,初应力σ0与等效节点荷载向量Fε0均是为了得到初应变εα计算过程中的产物,实际路基荷载引起应变的同时不会产生这样的应力场。
由有限元基本原理可知,总刚度矩阵K:
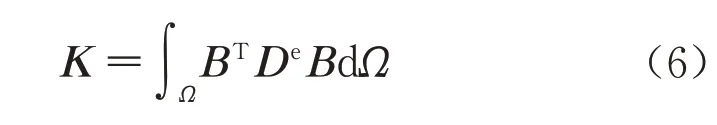
对比式(5)与式(6)可知刚度矩阵De的选取对总刚度矩阵K与等效节点荷载向量Fε0的影响完全同步,故只要在数值收敛的范围内,可以选取任意弹性矩阵De而不会影响节点位移向量。
以上过程相当于用初应变εa和弹性矩阵De算出一个等效节点荷载向量Fε0,让等效节点荷载在有限元模型中不断作用,以模拟循环荷载引起的变形,通过最小位能原理保证了这种变形是受力平衡且几何连续的,从而实现了以显式模型为本构模型的等效有限元计算。
基于黄茂松等[19-20]提出的可考虑土体初始平均围压、偏应力及动偏应力等影响的软黏土轴向累积应变公式,本文软黏土在循环荷载作用下轴向累积应变εc1计算公式为:

其中,D*d为修正相对动偏应力水平,描述第一次轴向循环累积应变,即:

式(7)—(8)中:pa为标准大气压;ps为围压;q*j为试样固结以后在不排水条件下施加的静偏应力。a、n值反映了修正动偏应力水平对第一次循环轴向循环累积应变与围压归一化值的影响,由第一次循环加载轴向循环累积应变与围压归一化值和修正动偏应力水平拟合得到;c反映了围压对第一次循环加载轴向循环累积应变的影响,由等向、偏压固结不同围压相同动应力比循环加载第一次轴向循环累积应变与围压通过指数拟合值取平均得到;b反映了循环次数对轴向循环累积应变的影响。
2.2 轴向累积应变模型的三维化
等效有限元方法的计算过程中需要计算6个应力分量方向上的累积应变,而经验公式通常不能给出各个方向的累积应变。理论上,三轴试验可以给出体应变增量和剪应变增量的表达式,但实际试验过程中,由于试验条件的限制,通常只给出轴向累积应变与循环次数等因素的关系,如式(9)所示。

式中:εc1为三轴试验轴向累积应变;A为与应力状态等因素相关的常数;而f(N)为与循环次数相关的函数,一般为对数或指数函数。
对于不排水黏土的循环三轴试验,循环过程中土体累积体应变为0,泊松比近似为0.5,因此轴向累积应变Δ及侧向累积应变Δ之间满足如下关系:

累积剪应变增量Δεcq:

一种实现轴向累积应变三维化的方式由Pasten等[14]提出,这种方法表达式如式(12)所示:

式中:1=[111000]T;σ为应力列向量(拉为正);p为平均应力;q为偏应力。根据式(11)和(12)可实现应变三维化。
2.3 等效有限元方法计算流程
桩土系统建模完成后,利用ABAQUS软件子程序UMAT可实现在不同分析步进行不同变量的计算。分析步的实现具体步骤为:①计算初始静应力场的分布,并根据初始应力场确定围压、静偏应力和静强度,即ps、q*j及qult;②将交通荷载简化,根据简化后的荷载计算地基中的附加动应力场,即qd=|qmax-qs|;③根据静动应力场及静强度的大小,由累积变形的经验公式计算一定循环次数下土单元的累积应变ε1acc;④将得到的累积应变作为初应变,计算出地基的沉降分布。
3 ABAQUS建模分析
如图6所示,模型长30 m、宽15 m、深40 m,约束除顶面以外各面的法向位移,采用实体单元,本构模型采用弹性模型;在桩土顶面有0.3 m的支承层(素混凝土)和0.4 m的基床表层,模型桩长20 m(此处参照设计要求,桩底位于⑤2层土),桩径0.5 m,桩纵向间距3.8 m,横向间距2.0 m。支承层采用C30混凝土现浇,图6a中高显部分为桩,其余为分层的土体,图6b中显示了支承层,图6c反映了荷载布置情况,结构部分模型参数见表1。因有限元模型中的桩、板和轨道三者始终保持位移协调状态,所以有利于减沉疏桩-路基板一体化沉降设计分析。
现代有轨电车设计轴重及时速均低于高铁、铁路、地铁等轨道交通形式,最高运行时速(70 km·h-1)运行时,单个轮轨动荷载最大值为151.25 kN,动荷载在路基面上均匀分布,大小为28.4 kPa,分布范围2.6×4.1 m。根据轨道的路基结构设计,本次计算范围为4.0 m×30.0 m(长边为沿轨道方向),在此计算区域内按绝大部分时间内有4个轮轴位于其上,因此路基面动荷载为

图6 模型三维示意图Fig.6 Finite element model

表1 结构参数取值Tab.1 Values of structural parameters

3.1 D089测点计算结果
各土层基本属性由工程勘探获得,土层剖面见图4,具体深度值见表2。利用GDS(公司名)系统对各软土层土样开展静力与循环三轴试验,原状土取自南方某轨道交通项目各层土,浅层易取土样采用PVC管保持竖直插入已找平的土层,在边上开挖将筒取出;深层土样采用钻杆取土,使用铁皮或取土器将取出的土封装并运至养护室养护。试样直径为39.1 mm,高为80 mm,分别进行σ'3c=100、150、200 kPa等向固结动应力比为0.1、0.2及偏压固结动应力比为0.06、0.1、0.2的循环加载试验,动应力比ηd定义为ηd=qdσ'3c,qd为动应力峰值。加载波形选用半正弦波形,加载次数均为6 000次,加载频率为1 Hz。试验过程土样处理如图7所示。对试验结果进行整理,并对各层软土的模量和累积变形公式所需参数加以标定,各软土层模型参数标定见表3。对于⑤2全风化花岗岩层,地勘报告显示其弹性模量为80 MPa、粘聚力c为30 kPa、内摩擦角φ为28°,这与庞小潮[21]对该地区全风化花岗岩的变形和强度指标研究结果基本一致。此外,庞小潮[21]还进一步开发了针对该地区全风化花岗岩弹塑性边界面本构模型,根据其标定的模型参数可知本工程埋深最浅的全风化花岗岩的边界面初始屈服应力165kPa,而经过试算发现有轨电车引发桩底土层的最大附加应力不足初始屈服应力的20%,因此本文近似采用弹性本构模拟全风化花岗岩的力学行为。

表2 D089和D206测点土层分布Tab.2 Distribution of soil layer for D089 and D206

图7 动三轴试验流程Fig.7 Process of dynamic triaxial test
如式(7)所示,显式模型公式的计算需要设定循环次数。有轨电车发车间隔5min·班-1,每运行一次,地基土受载循环3次,电车每天平均运营时间14 h。由此可计算有轨电车运营下,地基土应力循环次数约为18万次·年-1。按照此循环次数规律,确定每隔一个监测时间节点时的路基循环次数,即2017/07/29~2017/12/15对应60 000次,2017/7/29~2018/06/03对应150 000次,2017/07/29~2018/11/30对应240 000次,以及2017/07/29~2019/02/28对应340 000次,分别用有限元计算对应循环次数下的路基沉降值,图8显示了34万次循环后的竖向位移云图,图9对比了6万、15万与34万次的沉降剖面,随着循环次数增加路基板-疏桩基础引起沉降范围逐步扩大,使更深土体共同分担有轨电车引起的附加荷载。
将与监测时间节点所对应的循环次数下计算结果与实测值进行对比,如图10所示,等效有限元结果在6万次循环(工后5个月)沉降开展迅速,一年后沉降速率渐缓,对比显示等效有限元方法可合理反映路基的长期沉降规律。

图8 34万次循环竖直方向位移Fig.8 Vertical displacement of 340 000 cycles

图9 各个循环次数下竖直位移结果对比Fig.9 Comparison of vertical displacement results of each cycle

表3 土体模型参数Tab.3 Parameters of soil model
3.2 D206测点计算结果
D206测点建模与D089类似,不同的是此处桩长为18 m,各土层剖面见图4,该点的各土层参数如表3所示。同样分别用有限元计算对应循环次数下的路基沉降值,图11显示了34万次循环后的竖向位移云图,图12对比了6万、15万与34万次的沉降剖面,从自身沉降发展来看,D206测点与D089测点类似,随着循环次数的增加,沉降逐步向深层土体发展。但本测点淤泥质土层厚度到了D089测点处的4.5倍,导致需要更长时间才能使沉降趋于稳定,对比图9和图12发现本测点淤泥土层压缩量达到了D089测点淤泥层压缩量的3倍,这也导致本测点的绝对沉降比D089测点大80%。

图10 D089监测点计算结果与实测结果对比图Fig.10 Comparison of monitored and calculated results at D089

图11 34万次循环竖直方向位移(单位:m)Fig.11 Vertical displacement of 340 000 cycles(unit:m)
图13显示了计算与实测的沉降规律,对比可知,在较小的循环次数下(小于15万次),土体沉降发展迅速,地表位移响应明显增加,而随着循环次数的增加(大于24万次),土体沉降增长的速率变缓,此时可认为土体在地表结构和列车等荷载作用下逐渐达到稳定状态,此后的沉降增长将逐渐稳定。总体来讲,本等效有限元方法能较好地预测路基板-疏桩的长期沉降规律,并能够反映地基土不同所导致的沉降规律的差异性。
3.3 路基板-疏桩结构承载机理分析
本工程案例恰有较好的持力层,而对于我国东南沿海城市通常覆盖有深厚的软土层,为进一步探讨路基板-疏桩基础在无良好持力层情况下的承载特性,本文进一步以D089测点为例,采用相同土体参数与荷载工况条件,假定有轨电车在桩底仅进入④2砂质粘性土层2倍桩径,并分析其沉降规律;另外也对无砟道床基础(不考虑疏桩)进行分析对比。

图12 各个循环次数下竖直位移结果对比Fig.12 Comparison of results of vertical displacement of each cycle
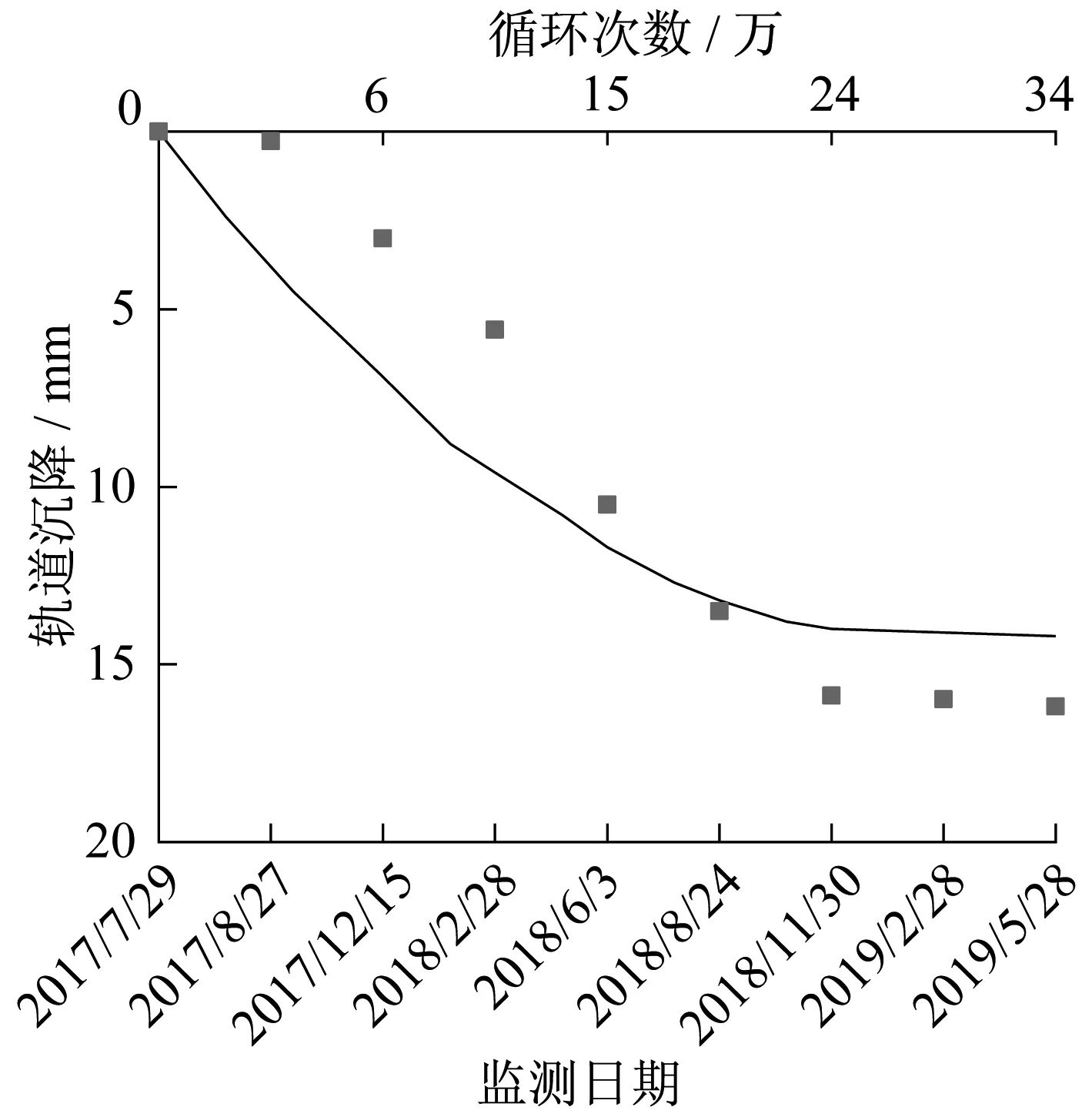
图13 D206监测点计算结果与实测结果对比图Fig.13 Comparison of monitored and calculated results at D206
沉降曲线如图14所示,在相同的运行时间里,无砟道床路基结构的沉降最大,运行4年左右,沉降已经超过规范限值;本工程案例得益于路基板-疏桩基础形式和较好的持力层,地表沉降仅为无砟道床结构的1/5左右;对于假设桩端进入④2砂质粘性土层2倍桩径的情况,从地表沉降来看,该算例的地表沉降小于无砟道床路基(无桩),且长期沉降符合规范要求,事实上,此算例的桩长仅为实际案例桩长的一半(11.5 m),且桩端以下仍存在较厚的软土层,这说明对于我国东南沿海覆盖有深厚软土层且没有良好的持力层的情况下,路基板-疏桩基础也可实现对有轨电车路基减沉的目标。

图14“路基板-疏桩”与“无砟道床”沉降对比Fig.14 Comparison of settlement of“track bed with sparse pile”and“ballastless track bed”
将三种基础形式下均循环70万次的位移云图进行对比,如图15a~图15c所示。在本文实际工程案例情况中,地表土体仅承担少量路基板荷载,合理发挥表层土体的承载作用,大部分列车荷载借由桩基传递到深层土体;反观“无砟道床”基础,列车荷载全部由表层土体承担,地表处过大的附加荷载使得路基沉降量达到了实际工程案例中的5倍,且沉降集中于浅层,较少向深层发展(见图15d);相较于前两种情况,桩底位于④2层时,桩顶路基荷载向深部土体的传递深度介于上述二者之间,地表沉降也介于二者之间,从沉降分布云图和中心剖面沉降图可以看到,桩基础可以将有轨电车荷载传递到更深层土体,使桩底土和路基板下浅层土共同分担荷载,保证各层土体均处于低应力水平,可以有效降低总沉降。上述算例说明,在软土地区,若“无砟道床”基础无法满足有轨电车路基沉降要求,可考虑采用路基板-疏桩基础进行减沉控制;若软土层深厚且无良好持力层情况下,可采用等效有限元预测路基板-疏桩基础长期沉降,并根据沉降要求对桩长进行优化设计,在实现减沉控制目标的同时保证经济性。

图15 70万次循环荷载下路基沉降位移云图对比Fig.15 Comparisons of settlement contours at 700 000 cycles
4 结论
本文从南方某实际有轨电车项目出发,对“路基板-疏桩”这种新型有轨电车路基的长期沉降加以监测。减沉疏桩的设置虽无法完全消除工后总沉降,但可有效控制路基沉降,使工后沉降更快趋于稳定。对于不均匀沉降,减沉疏桩一方面可以改善整体地基土性的差异,通过控制绝对沉降以实现间接控制不均匀沉降;另一方面在深厚软土地层中通过桩基传力机制,使有轨电车荷载传递至深层土体,使软土层整体处于低附加应力状态,降低产生差异沉降的可能性更低。
又以此项目的路基形式为依托,开展对“路基板-疏桩”路基长期沉降等效有限元方法的研究,利用ABAQUS的自定义材料子程序UMAT开发了基于等效有限元理论的分析平台,选取此项目中两个较为典型的测点进行沉降模拟分析。从两个测点的有限元计算结果来看,本文采取的等效有限元方法可有效模拟“路基板-疏桩”这种路基形式的沉降发展规律,计算结果与实测值的误差在工程可接受范围内。本文所采用的方法所需土体参数较易获得,等效有限元方法能够简化较大的循环次数带来的计算时间问题,能够有效解决此类长期沉降计算问题。
基于实际工程案例,进一步探讨了减少桩长对有轨电车路基长期沉降的影响,结果表明:随着桩长的减少沉降显著增加,其中无砟道床路基的长期沉降将超过规范容许值,因而对于软土地区的适用性较差;路基板-疏桩基础在无良好持力层的情况下也可达到减沉的目的,且可通过等效有限元的对其长期沉降进行预测分析,从而实现对疏桩基础的优化设计。
作者贡献申明:
徐正良:课题来源、监测数据、分析方法概念;
刘磊:分析方法实现;
王浩然:监测数据处理;
俞剑:分析方法指导、文章编辑;
黄茂松:分析方法概念。

