异步化高压发电机失磁故障分析
石建飞, 戈宝军, 吕艳玲
(1.哈尔滨理工大学 电气与电子工程学院,哈尔滨 150080;2.黑龙江八一农垦大学 电气与信息学院,黑龙江 大庆 163319)
0 引 言
失磁故障属于大容量发电机组常见的故障类型之一,因发电机组励磁系统复杂并有较多的环节组成,导致失磁故障明显增多。由于失磁故障可导致发电机局部发热、励磁系统过电流等现象,最终引发电网崩溃,给大型发电机组稳定可靠运行带来影响。发电机失磁后通常将工作在异步状态下,由于转子转差的出现,转子将出现过热的现象;定子电流大小也因失磁故障而增加,导致定子铁心过热;发电机由于失磁故障会向电网吸取大量无功功率,同时有功功率输出将明显减少,从而使系统中部分设备,例如发电机、变压器或线路等元件,可能发生过载,引起相应元件的后备保护误动作,使故障范围进一步扩大,对整个系统稳定运行带来威胁。
在同步发电机失磁故障的研究中,国外学者多以路为基础来建立模型进行仿真分析。Raju D Rana等以路为基础建立电机模型,针对机组并网工作时发生失磁故障进行仿真研究。Les M Hajagos等采用动态仿真的方法对发电机组失磁后的稳定性进行研究,证明了该方法的有效性。Rodriguez O等研究发现,当机组失磁故障发生后,尽管进入到稳态异步运行状态,仍可通过励磁系统的调节,恢复发电机运行于同步状态[1-4]。文献[5]中,东方电机公司的研究表明,当机组因短路故障失磁时,机组对电网输出的功率,同时包括电机转差的变化以及定子电压和电流的波动均大于开路失磁,考虑到电网容量范围,虽然电机在失磁状态下,也将向系统发出有功功率。文献[6]中,姚晴林从滑差影响因素的研究出发,通过实时在线监测滑差变化情况,来判定机组失磁后的工作状态,当滑差超过允许的最大值时,应发送切除发电机指令,将机组断开起到保护的作用,从而避免事故扩大。文献[7]中,马波涛等利用MATLAB建立失磁故障仿真模型,通过仿真分析发现,针对不同故障条件,转子在失磁后,将在低转差工况运行,随后再返回到以前转差所对应的稳定异步运行,并呈现周期性,同时发现当发电机具有灭磁电阻时,电机对系统影响将小于无灭磁电阻的情况[5-7]。
国内诸多学者都利用场的方法(有限元分析法)对失磁过程进行深入研究。文献[8]中,刘立军通过对不同的失磁情况下电机的参数、气隙磁密等变化规律的分析,开路失磁进入稳态异步运行比短路失磁更容易,如果故障前机组承载较大负荷,就较难使机组快速恢复到之前的稳态异步运行。文献[9]中,梁艳萍教授建立汽轮发电机数学模型和转子端部三维涡流磁场模型,以有限元分析方法准确得出转子端部漏磁参数及涡流损耗的变化受不同转差率工况下的影响,改进了以修正系数来克服端部影响而产生的不足[8-9]。
目前,学者对于超高压发电机发生失磁故障的研究不多,文献[10]通过建立失磁后超高压发电机的变参数模型、二维物理模型和三维温度场模型,利用失磁动态仿真和二维场路耦合计算,分析了失磁故障时,机组的气隙磁密、磁场分布、温度场分布等的变化情况,在建模过程中,由于励磁绕组与直轴阻尼绕组存在互感漏抗,因此在分析时将此漏抗的影响加以考虑,这样对发电机在不同运行工况下的分析就更加准确[10]。
异步化超高压同步发电机是将异步化同步发电机与超高压同步发电机的特点有效结合,其定子绕组由交联聚乙烯电缆,可以输出较高电压,转子通过变流器连接电网具有较好的调节特性。目前,国内对于异步化超高压同步发电机在发生失磁故障的研究还处于空白,因此本文对异步化超高压发电机失磁故障的研究与分析,为高压发电机的继电保护提供基础数据。
1 问题假设
为了简化问题分析,突出所研究重点,提高建立数值计算模型适用性,达到实用的目的,本文对超高压发电机提出以下假设:1)电机与无穷大容量系统直连时,定子端电压将保持不变;2)如图1所示,将电机结构分割成直线部分与端部,直线部分以时步有限元法对二维电磁场进行分析,端部则以解析计算法将其参数计入支路内进行分析;3)各变量的参考正方向与“路”的方法研究过程中保持一致;4)由于定、转子材料具有非线性特性,为了研究简化,可在分析过程中忽略磁滞损耗、涡流损耗以及轴对称性的畸变误差带来的影响;5)电机材料的电导率假定为常量。
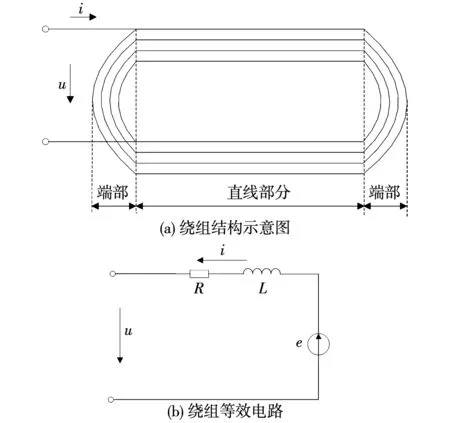
图1 异步化高压同步发电机绕组模型Fig.1 Wingding model of asynchronous high synchronous generator
2 模型的建立
异步化高压同步发电机的系统接线图如图2所示,异步化高压同步发电机三相定子绕组与电网直接连接,转子侧绕组则通过变流装置进行交流励磁,实现两条通路完成能量传递。图2中发电机通过变桨距控制方式,且异步化高压同步发电机转子通过变流器与电网进行能量双馈完成转子的交流励磁,其特点是通过对转子电流的控制来调节电机输出功率,使发电机运行在最大功率附近。

图2 异步化高压同步发电机系统接线图Fig.2 Asynchronous high synchronous generator system connection diagram
其定子绕组为Y型接线,电路中所示的电压与电流的参考方向如图3所示。
根据图3可建立定子回路方程为:
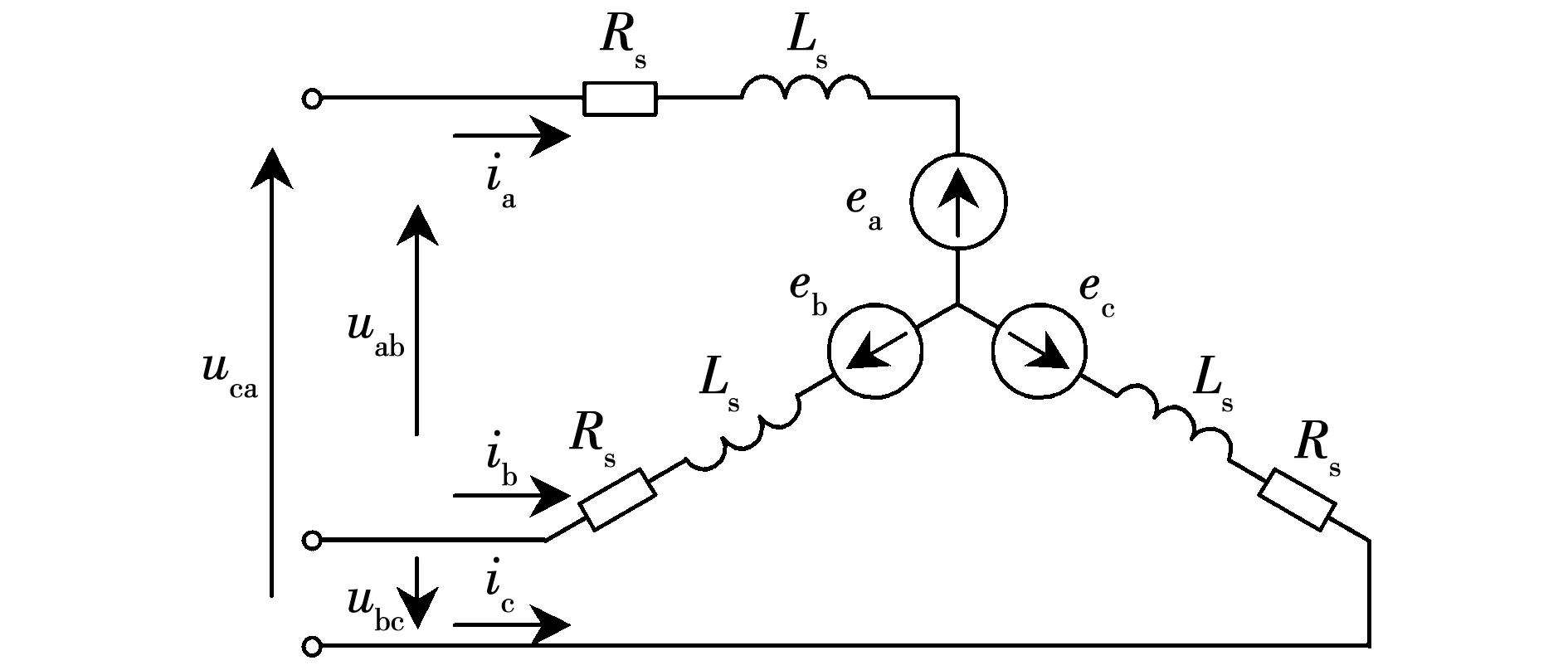
图3 定子回路及参考方向Fig.3 Stator circuit and reference direction
(1)
式中相绕组感应电动势可用向量磁位表示为
(2)
式中:NS为每槽绕组匝数(或励磁绕组的匝数);S为某相电流(或励磁电流)流出或流入端(如A或X等)导电区域的总面积;N为某相绕组流入、流出导电区域的单元总和;Leff为电机的轴向有效长度;当单元位于绕组电流流入端如A、B、C导电区域时,p=1,否则p-1。
将式(1)和式(2)中变量I、∂A/∂t、dI/dt改写成向量矩阵方程为
(3)
其中:Us、Is分别为定子三相电压和电流的列向量;M、Rs、L各变量的系数数矩阵。
异步化超高压同步发电机转子绕组回路的等效电路如图4所示,正常运行和失磁故障可通过k1~k7这些开关组合来等效。
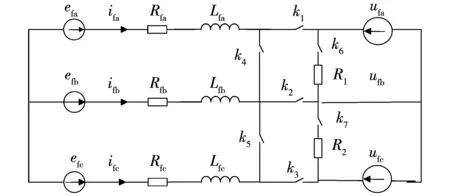
图4 转子绕组回路等效电路图Fig.4 Equivalent circuit diagram of rotor winding loop
图4中,正常运行时,可以通过将k1、k2、k3闭合,同时k4、k5、k6、k7打开来等效;当励磁绕组三相出现短路故障而失磁时,可将k1、k2、k3打开,同时k4、k5、k6、k7闭合来等效;A、B两相短路失磁时,可将k1、k2、k5、k7打开,同时k3、k4、k6闭合来等效,根据图4得到转子绕组电路方程为:
(4)
根据等值电路列出回路矩阵方程为
(5)
其中:N、Rr、Lf为变量If、A/t、dIf/dt在转子回路中对应的系数矩阵。式(5)参数k表示失磁的程度,k通过开关进行模拟,闭合时k1,模拟短路失磁,断开时k=∞,模拟开路失磁,k为其他值可模拟部分失磁。
将式(3)和式(5)联立可得到异步化高压发电机场路耦合方程组为
(6)
3 仿真结果与分析
仿真系统中电机定子三相绕组采用Y接方式,其主要参数如表1所示。
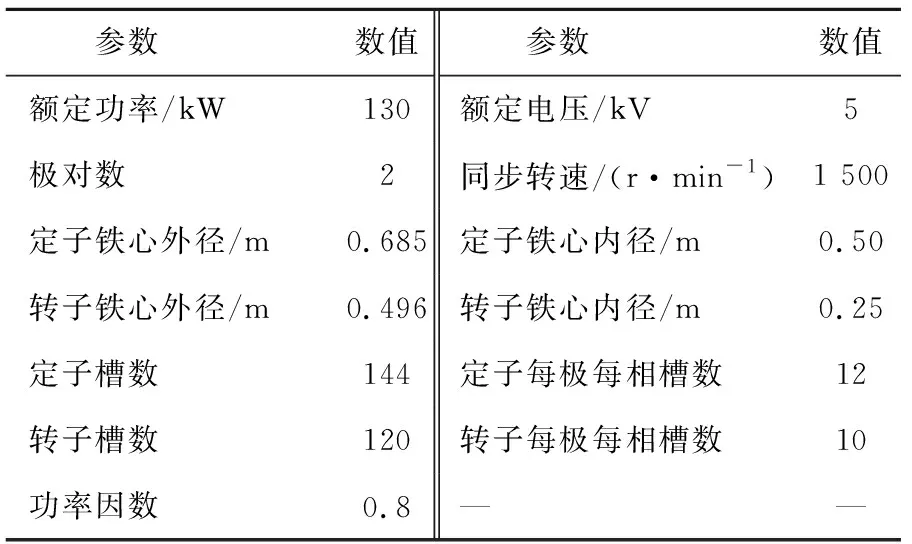
表1 电机参数Table 1 Electric machine parameter
3.1 异步化高压发电机对称失磁故障分析
利用上述已经建立的仿真系统分析异步化高压发电机对称失磁故障。图5为s=0和图6为s=-0.2两种情况下,异步化高压发电机额定稳态运行及失磁运行时一个磁极下的气隙磁密云图。

图5 s=0失磁前后磁力线分布和磁通密度云图Fig.5 Magnetic field line distribution and magnetic flux density before and after loss of excitation when s=0
从图5可知:异步化高压发电机在正常工况下的磁密与磁力线分布,在突然发生对称故障时,失磁后电磁场分布保持均匀。尽管定、转子铁心的磁通密度都改变,但是在其对应的气隙处最为明显。齿部磁密、轭部局部磁密和气隙磁密均变大。
由图6可知:s=-0.2时,发电机发生故障失磁后导致电机的齿部、轭部局部、气隙三处磁密都变大。对比图5和图6可知,s为-0.2时的磁密略大于s为0时的磁密。主要是由于在分析前假设电网电压为常量,因此电机的端电压应与系统电压保持一致。因电机失磁导致磁场减弱,为了维持机端电压为常量,异步化高压发电机需要电网来提供无功电流用于补偿减弱的磁场,使气隙中的合成磁场维持恒定。
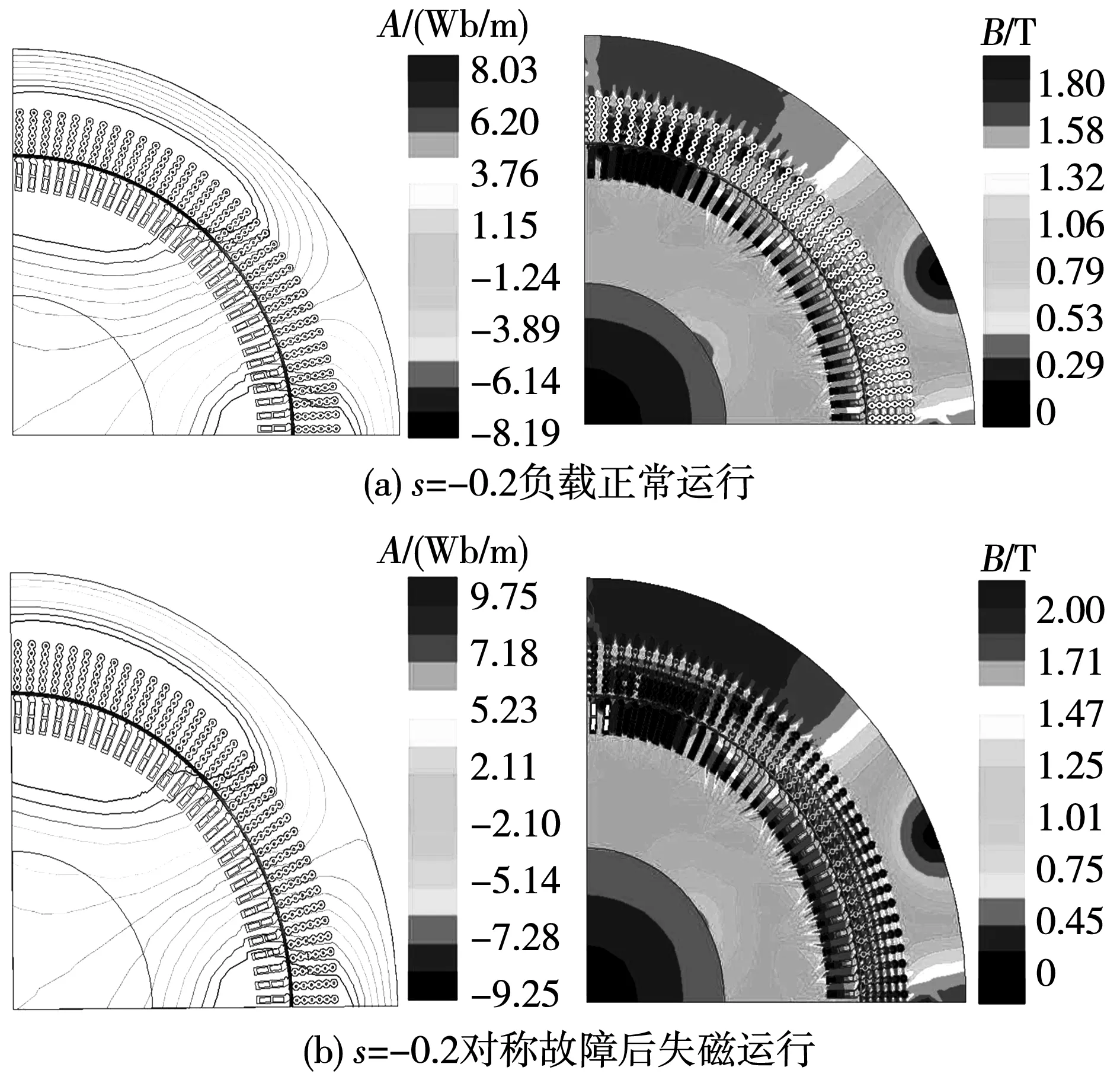
图6 s=-0.2失磁前后磁力线分布和磁通密度云图Fig.6 Magnetic field line distribution and magnetic flux density before and after loss of excitation when s=-0.2
通过在不同转差率下对气隙磁密进行谐波分析。当s=0和s=-0.2时,异步化高压发电机失磁前后的气隙径向磁密及谐波分析分别如图7~图8所示。
在图7(a)中,异步化高压发电机正常运行时,气隙磁密波形具有较好的对称性,呈正弦分布,高次谐波磁场幅值较小。图7(b)与(a)相比发现,气隙磁密的波形发生明显变化,最大绝对值有明显增加。其中,气隙磁场基波幅值增加较小,因为电机的定子绕组与系统直连,故电机端口电压与系统电压一致。因电机失磁导致磁场减弱,同样为了维持机端电压为常量,异步化高压发电机需要电网来提供无功电流用于补偿减弱的磁场,使气隙中的合成磁场维持恒定,电机端口电压也将保持不变。同时,5次和7次谐波幅值也略有增加。
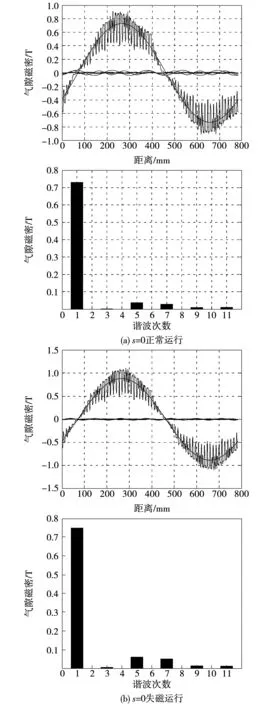
图7 s=0失磁前后气隙径向磁密波形及谐波分布Fig.7 Air gap flux density and harmonic distribution before and after loss of excitation when s=0
从图8可知:额定工况下,当s为0时,气隙磁密的谐波分布中高次谐波幅值均有增加。s=-0.2运行情况下,3、5、7次谐波幅值比s=0时的幅值明显增加。
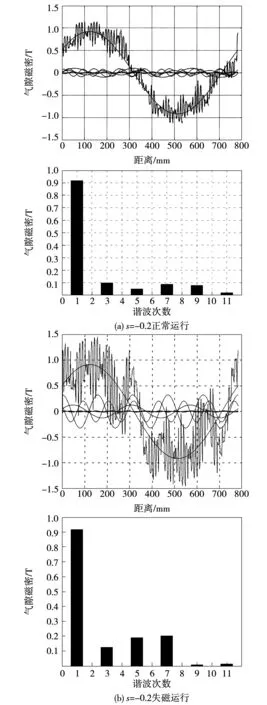
图8 s=-0.2失磁前后气隙径向磁密波形及谐波分布Fig.8 Air gap flux density and harmonic distribution before and after loss of excitation when s=-0.2
异步化高压发电机定子绕组会因短路故障的发生使感应电流变大,这会导致电机绝缘被破坏,使绕组本身也产生一定的损坏,因此通过分析异步化高压发电机转子在失磁前后主要电气量变化特点,在工程上具有重要意义。在s=-0.2和s=0工况下,对称故障在失磁前后定子A相电流曲线及谐波分析如图9和图10所示。
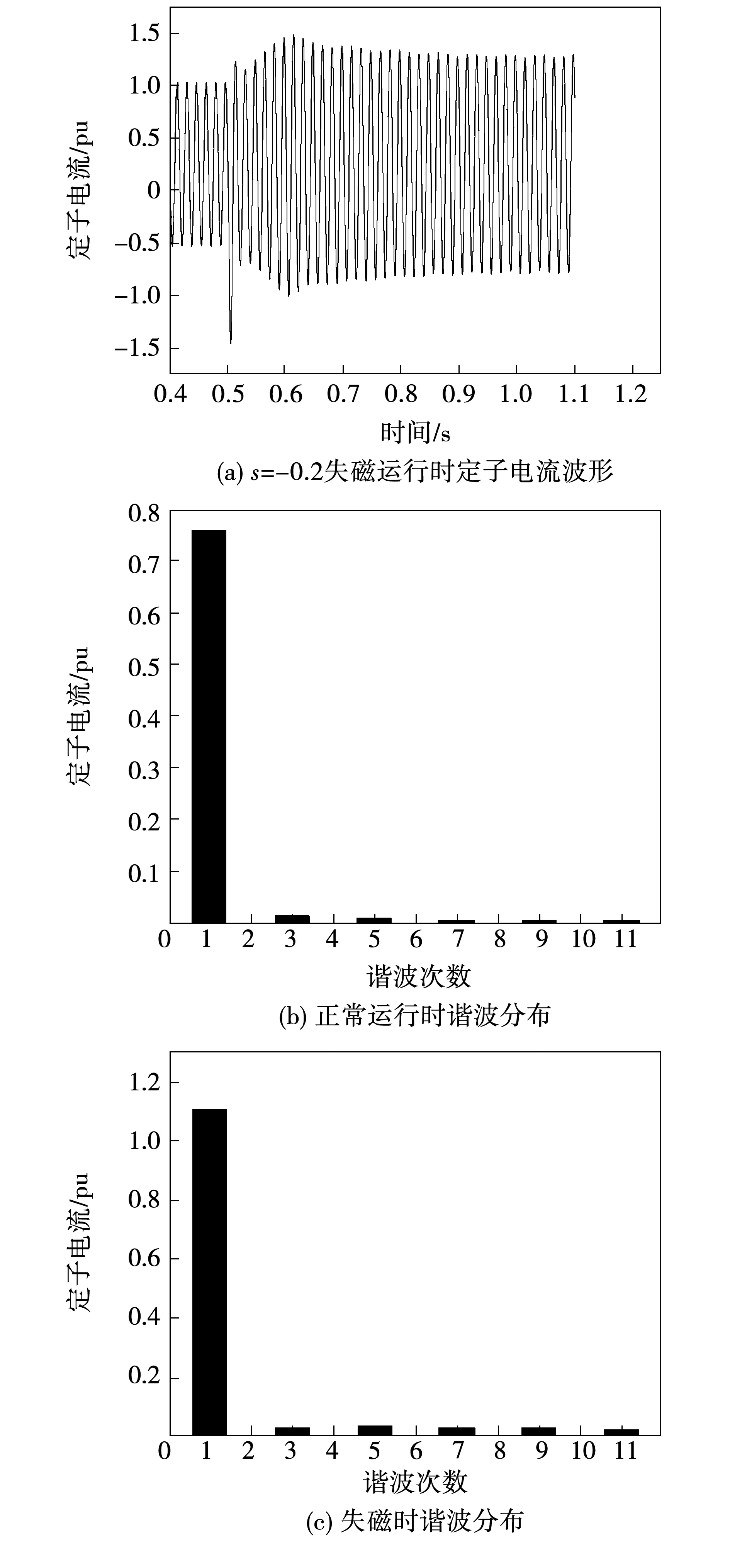
图9 s=-0.2失磁前后定子A相电流波形及谐波分布Fig.9 Current wave and harmonic distribution of stator of A phase before and after loss of excitation when s=-0.2

图10 s=0失磁前后定子A相电流波形及谐波分布Fig.10 Current wave and harmonic distribution of stator of A phase before and after loss of excitation when s=0
由图9可知:在电机额定工况下其定子电流波形以基波为主,含有较少的谐波成分;当0.5 s时,转子三相绕组出现对称短路故障后,导致定子电流突然增加到额定电流的1.5倍。当发电机出现对称短路时,变流装置因无法为转子励磁,故在故障初期仅转子剩磁起作用,经0.2 s后,发电机达到相当于异步电动机稳态运行的新状态,发电机通过定子从系统吸收无功功率来建立磁场。在发生对称短路故障后,定子电流感应出大量谐波,且各次谐波幅值均有明显增加。
从图10可知:当失磁产生后,定子电流幅值在不断增加并产生振荡。电流波形中包含大量谐波成分,且基波成分增加明显。转子失磁故障对并网运行的异步化高压发电机存在相当严重的危害。定子绕组在发生故障时,会出现较大的感应电流,可能在短时间内对绝缘和绕组线圈均有损坏。由于定子电流增大也会使后备保护动作,使故障波及范围变大,导致严重后果。
3.2 异步化高压发电机不对称失磁故障分析
条件假设:系统中异步化高压发电机失磁可带额定负载进入稳定运行状态,电机并网运行过程中,端口电压保持恒定。当s=0和s=-0.2时,异步化高压发电机分别在额定负载和转子两相短路失磁两种工况下,单极磁力线和气隙磁密分布云图如图11和图12所示。
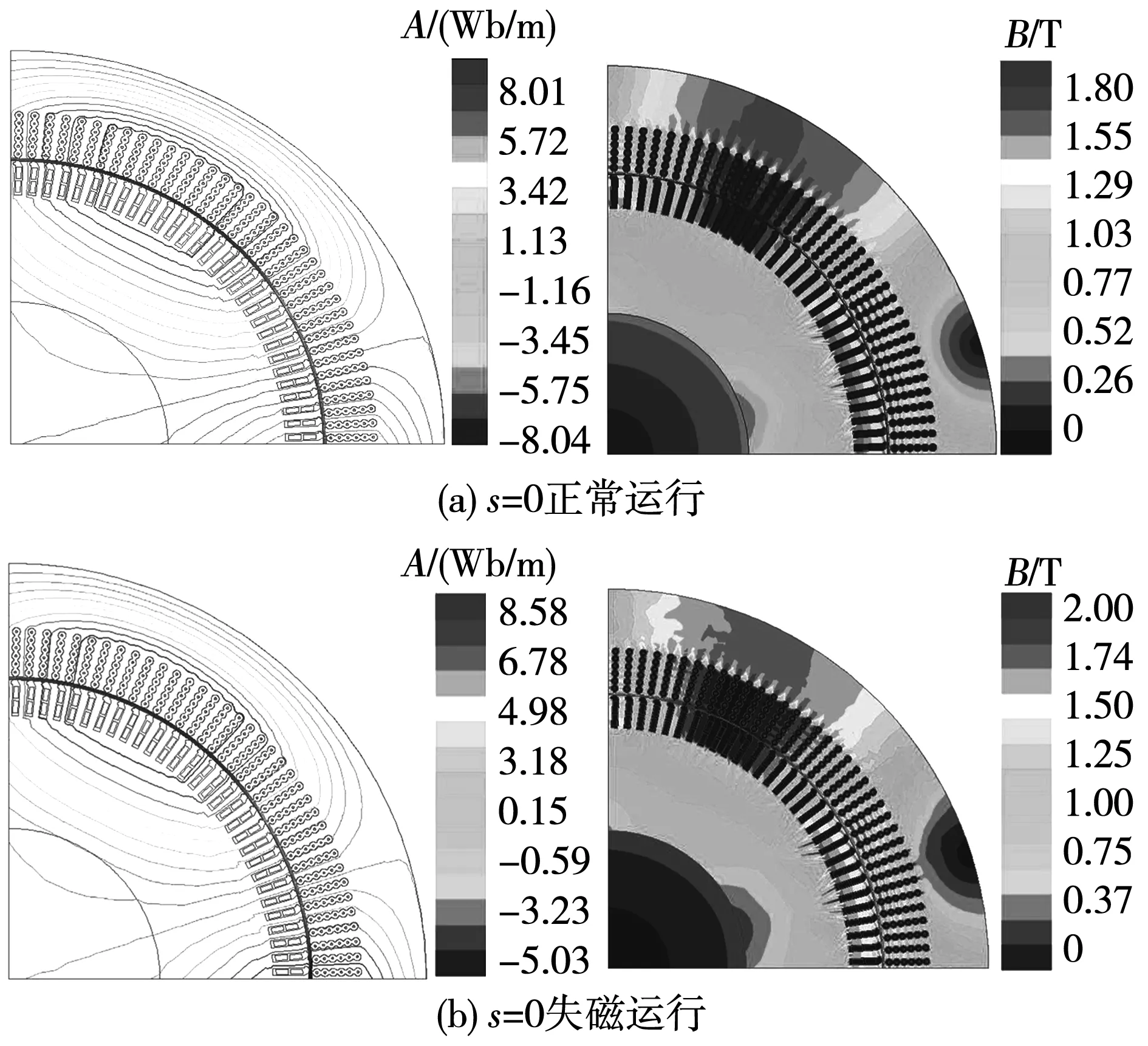
图11 磁力线和气隙磁密云图Fig.11 Magnetic field line and magnetic flux density

图12 磁力线和气隙磁密云图Fig.12 Magnetic field line and magnetic flux density
当转子绕组发生转子两相短路时,定、转子铁心的磁通密度都发生变化,其气隙处变化最为明显。由图11(a)、图11(b)、图12(a)和图12(b)可以看出,不同转差工况运行下,磁力线分布规律改变,同时磁密增大的位置也受到影响,且s=-0.2时的磁密大于s=0。齿部磁密、轭部局部磁密和气隙磁密均变大。在s=0时,异步化高压发电机发生转子两相短路故障时,与额定稳态时相比,其磁通密度最大值增大,且最大磁密相差0.2 T,齿部铁心出现过饱和。
从图13和图14可知:由于转差率的不同,并网运行后,异步化高压发电机在s<0时运行,失磁故障前后的气隙径向磁密和谐波分布如图13~图14所示。
从图13(a)和图13(b)对比可知:当异步化高压发电机发生两相短路故障后,由于转子电流的变化导致转子磁场也随之发生变化,从而合成气隙磁场发生畸变,主要表现在失磁后基波、3次、5次谐波幅值增加,且3次和5次谐波增加程度大于基波,7、9、11次谐波幅值相反而减小,可见,异步化高压发电机在同步运行下,气隙磁场中高次谐波变化受两相短路影响较大。
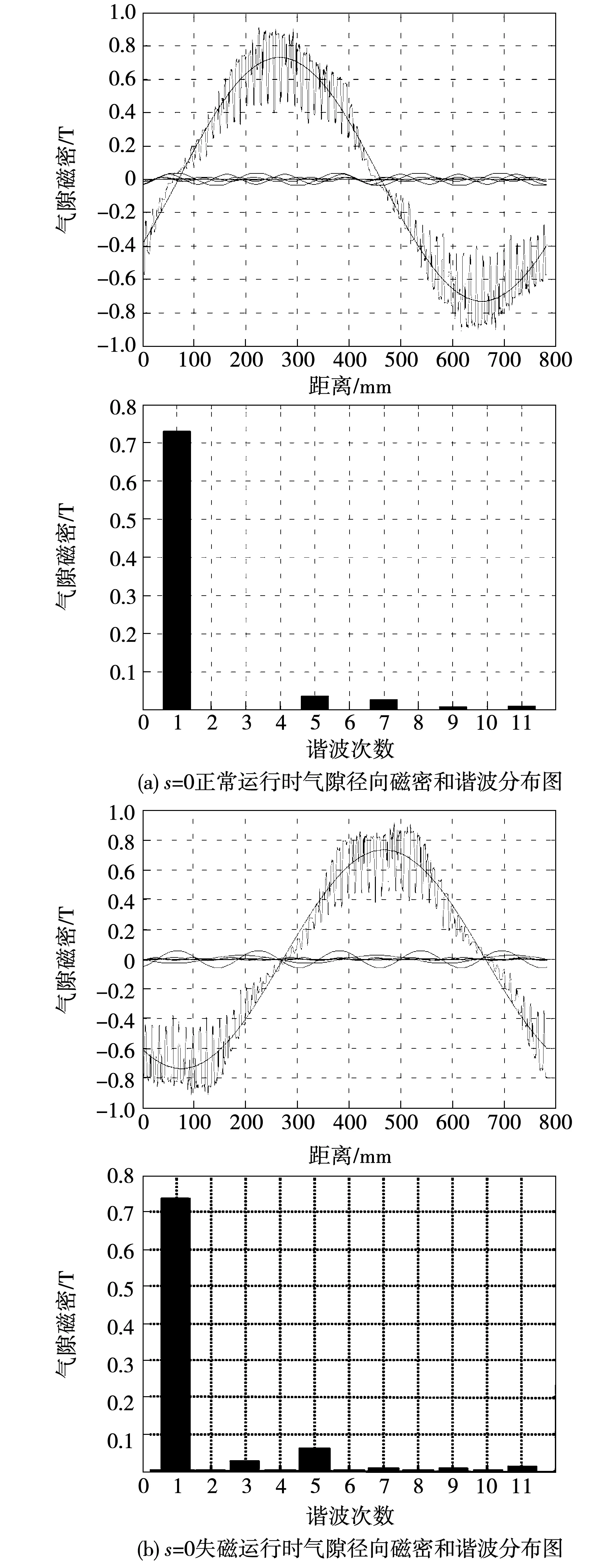
图13 s=0失磁前后气隙径向磁密和谐波分布Fig.13 Air gap flux density and its harmonic distribution before and after loss of excitation when s=0
从图14(a)和图14(b)对比可知:异步化高压发电机在s<0时运行,励磁绕组两相短路故障后因转子电流发生变化,并在定、转子磁场共同作用后,合成的气隙磁密在幅值上略有减小。其中,只有5次谐波略有增加,而其他高次谐波与正常运行时相比均有减小。可见,异步化高压发电机在此工况下,两相短路对气隙基波和高次谐波还是有明显影响。

图14 s=-0.2失磁前后气隙径向磁密和谐波分布Fig.14 Air gap flux density and its harmonic distribution before and after loss of excitation when s=-0.2
s=-0.2时,异步化高压发电机转子发生两相短路故障时,失磁前后其定子单相电流波形以及正常运行和故障运行时谐波曲线分别如图15(a)、(b)和(c)所示。
从图15(b)可知:异步化高压发电机在正常运行工况下,定子电流中除了基波分量外,谐波分量很小。通过仿真设定在t=0.5 s时电机转子发生两相短路故障情况下对定子电流进行分析,由图15(a)和图15(c)可知,定子单相电流增加到正常运行时的4.2倍。由于转子发生两相短路削弱发电机励磁作用,仅由转子的非故障相承担励磁,因此电机的短路电流呈衰减趋势,并在0.8 s后进入新的稳态,其稳态值约故障前3倍,且故障后电流基波分量增加而谐波分量不大。
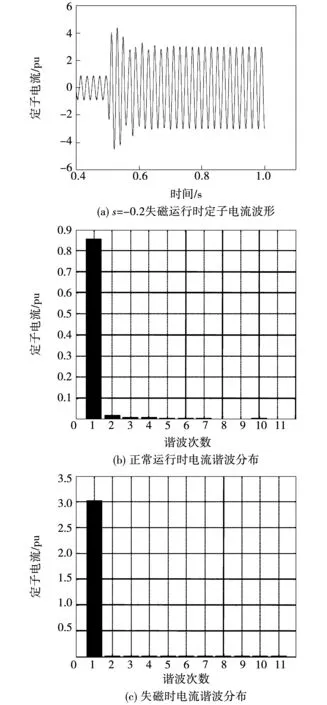
图15 s=-0.2失磁前后定子A相电流波形和谐波分布Fig.15 Current wave and harmonic distribution of stator current of single phase before and after loss of excitation when s=-0.2
当s=0时,电机转子两相短路故障失磁前后定子单相电流波形以及正常运行和故障运行时谐波分布情况分别如图16(a)、(b)和(c)所示。从图16(a)可知:异步化高压发电机两相失磁后定子单相电流出现不断增大并伴随振荡现象,运行至2.5 s后进入新的稳态。与转子对称故障失磁相比,定子电流中所含谐波有增长趋势,进入稳定状态的时间明显增长,因此可根据电机故障后稳定所需的时间作为检测异步化高压发电机发生不同类型故障的参考标准,提高故障类型判定的准确性。

图16 s=0失磁前后定子A相电流波形和谐波分布Fig.16 Current wave and harmonic distribution of stator current of single phase before and after loss of excitation when s=0
4 结 论
本文建立了异步化高压发电机的场模型及失磁系统的场路耦合模型,利用该模型对转子绕组对称与非对称失磁故障进行了分析,得出了异步化高压发电机转子在发生对称短路与非对称短路故障失磁前后,其产生的气隙磁场和定子感应电流的变化规律。在短路故障时,转子绕组产生气隙磁密的波形变化明显,谐波含量随转差率的增大而增多。
当转子绕组发生短路失磁时,由于异步化高压发电机的定子绕组与电网直接连接,其端电压不发生变化,发电机一定要从系统吸收无功电流来补偿因故障而减弱的磁场。
当转子绕组因两相不对称短路故障而失磁时,都会引起定、转子铁心的磁通密度改变,且磁密增加位置也会因转差不同而不同,当s=-0.2时,磁密幅值比同步运行状态下略大,定子电流幅值约为额定工况下的3倍,其谐波含量明显增加,研究内容可以为异步化高压发电机故障检测提供数据支持。

