基于坝壳湿化过程数值模拟的心墙坝初蓄水力劈裂机理研究

邓 刚，陈 辉，张茵琪，张延亿，张幸幸，侯伟亚

（中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038）

1 研究背景

土质心墙土石坝简称心墙坝，是水利水电工程常用坝型，世界已建最高土石坝（塔吉克斯坦Nurek坝，高300 m）和中国已建最高土石坝（糯扎渡，坝高261.5 m）均为心墙坝，我国在建的两河口、双江口及规划设计中的RM等300 m级特高坝也均为心墙坝。历史上心墙坝曾发生多次疑似水力劈裂的突然渗漏甚至溃决事故，而研究中一直未能再现非预设缺陷情况下水力劈裂所需应力条件，心墙坝水力劈裂机理是亟待解决的安全问题之一。

本文从历史上疑似发生水力劈裂的心墙坝案例共性出发，分析了水力劈裂发生需要的必要条件，从理论上探讨了蓄水过程中心墙、坝壳的变形增量来源及其与坝壳湿化变形瞬时发生或持续发生间的关系，提出水力劈裂可能与坝壳湿化变形时间过程存在密切联系。探讨了粗粒料湿化变形与时间存在联系的原因，结合既有试验、根据经验建议了湿化变形时间发展过程模型即湿化后长期变形模型，并对假想模型坝开展了数值模拟，再现了初蓄过程中水力劈裂破坏所需应力条件。针对可能与水力劈裂发生存在联系的各因素，提出了相应建议。

历史上的疑似水力劈裂案例包括世界上唯一的高心墙坝溃决案例即美国Teton坝［1-3］和临近溃决、紧急降低水位后得以残存的美国Fontenelle坝［4-5］，以及多个在一过性突然渗漏后未溃决的案例［6-7］，如英国 Balderhead［8］、挪威 Viddalsvatn［9］和 Hyttejuvet［10］、美国 Yard's creek［6］和新西兰 Matahiña［11］等，2000年后我国建成的毛尔盖心墙坝也曾发生了类似的一过性突然渗漏。

考虑到心墙采用的黏土、砾石土与坝壳采用的堆石、砂砾石等粗粒土间的力学特性差异，过去研究中曾较多将水力劈裂原因简单归咎于该差异可能导致的拱效应和心墙竖向应力减小，并进一步认为“竖向应力小于库水压力”并引发心墙内部水平裂缝和水力劈裂。从概念上看，水力劈裂本质是张拉破坏，土体外部水压力高于土体总小主应力（及与抗拉强度之和）时，水力劈裂将在小主应力正交面上发生，这在采油、劈裂灌浆等实践中早已验证［12］。因此，心墙坝是否发生水力劈裂，既取决于小主应力数值（小主应力为负，即拉应力），又取决于小主应力方向（小主应力正交面需穿透心墙）。

心墙中竖向应力的正交面正好对应穿越心墙的水平裂缝，同时，心墙中实测竖向应力一般也确实明显小于上覆土重，因此，早期水力劈裂研究中，内部裂缝被狭义为横断面上的水平裂缝，竖向应力替代了小主应力，被用于水力劈裂判别。实际上，心墙“竖向应力小于库水压力”这一条件，不仅从没有在实际中测得过；在不考虑心墙施工导致的既有缺陷、裂缝及由此引起的尖端应力集中和高压水楔劈致裂情况下［13-15］，也未能在数值模拟、物理模拟中再现过。由于竖向应力往往接近大主应力、远大于小主应力，因此，以竖向应力小于水压力作为水力劈裂判据在工程中无疑是过于宽松且不合理的。而单纯从该条件出发，可能导出坝壳压实偏于有害的结论，以减小拱效应为目的而放松坝壳压实密度和模量要求，反而易导致后期变形过大（如蓄水过程中变形大幅突增）等问题［16］。

心墙中的小主应力多沿河流方向，因此，即使小主应力为负，看起来也不可能具备水力劈裂所需应力方向条件。

为了更好追溯历史上各疑似水力劈裂案例的原因，邓刚等［16-17］分析了各相关工程在体型结构、渗漏现象、应力变形等方面的特征。这些工程既包含了直心墙坝，又包括斜心墙坝，即使是直心墙，体型也有较大差异，可见，直心墙中可能的较强拱效应与破坏现象没有明显关联。同时，这些工程的监测资料也并无心墙竖向应力小于库水压力的情况。

值得注意的是，各工程渗漏量突增均发生在首次蓄水、水位快速上升过程中，且破坏位置都发生在岸坡中上部、存在坡面外凸转折等特殊地形的断面，而并非拱效应突出、变形大、水头高的河床附近典型大断面。同时，Hyttejuvet和毛尔盖等工程都存在坝顶沉降随水位快速上升而突增的现象，首次蓄水期间的坝顶沉降增量分别超过0.8 m［18］和0.6 m。

从案例分析上看，有理由猜测，坝壳压实度低、蓄水变形增量大（包含湿化变形等后期变形），在与岸坡存在外凸转折，水位快速上升等条件组合情况下较易出现水力劈裂破坏。其中，坝壳较大湿化变形及其过程、岸坡条件等尚未得到充分考虑，可能是过去的分析中难以计算得到水力劈裂所需应力条件的原因。

2 初蓄水力劈裂破坏与湿化变形时间发展过程关系的理论分析

2.1 湿化变形瞬时发生不能引发水力劈裂所需应力条件 随着蓄水过程中水库水位快速上升，水位以下的坝壳浸水并发生湿化变形。水位变动区的坝壳孔隙水压力提高后，有效围压降低［19］、发生卸荷回弹，同时剪应力水平提升、发生剪切变形并抵消部分卸荷回弹变形。水位以下的心墙中，库水渗入，孔隙水压力变化（视施工时产生的超静孔隙水压力及其消散情况）而卸荷回弹或受荷压缩。由于库水入渗心墙速度相对较慢，且入渗后水头从上游侧至下游侧逐步衰减，孔隙水压力变化量在心墙内不均匀分布，因此，心墙因库水入渗而导致的变形增量量级相对较小，在时间上也相对滞后于坝壳。

对于水位变动区之外的坝壳，在水位变化过程中，高程低于水位变动区的部分也因有效围压持续降低而略有回弹。高于水位变动区的坝壳则应力不发生变化，仅因为其下部坝壳的变形而同步发生抬升或沉降等变形。同时，由于回弹模量远高于加载模量，一般认为跟随水位变动区卸荷回弹变形发生的抬升变形量级较小。

如果认为坝壳湿化变形也随浸水过程即时完成，则坝壳各位置的湿化变形总瞬间发生在该位置是水位变动区时（即库水刚超过该位置所在高程时），且随着水位上升不再变化。因此，库水位上升增量仅导致当前库水位附近水位变动区内的坝壳湿化沉陷和卸荷回弹变形，由于湿化变形全部发生，该部分变形增量以沉降为主；库水位以下非当前水位变动区处，坝壳不再发生湿化变形而发生卸荷回弹（上抬）。无论坝壳湿化变形大小，水位变动区附近的心墙因与坝壳相互作用而主要发生局部压缩，但不会在特定位置特别是岸坡中上部断面因张控而出现应力局部减小至小主应力小于库水压力的情况，如图1所示。

图1 坝壳湿化变形瞬时发生时库水位快速上升导致的横断面上坝壳和心墙变形增量分布

2.2 湿化变形延时发生可能引发水力劈裂所需应力条件 如果湿化变形在浸水后延时发生，并持续一定时间，则当前库水位以下各深度处坝壳湿化变形持续增大，且随着水位上升仍继续变化。

对于一定的库水位增量，水位变动区内的坝壳变形增量与考虑湿化瞬时发生类似，存在卸荷回弹变形、剪切变形与浸水湿化变形的叠加，但一定时间增量内的湿化变形增量较小，因此，水位变动区的坝壳变形主要体现为回弹变形；而水位变动区以下的坝壳变形增量则与前述假定坝壳湿化变形瞬时完成的情况不同，持续存在湿化沉降变形增量。由此，考虑湿化变形持续时间后，库水位提高时，坝壳下部下沉而上部抬升，心墙则因与坝壳的相互作用而在中上部位置出现集中拉伸，如图2所示。

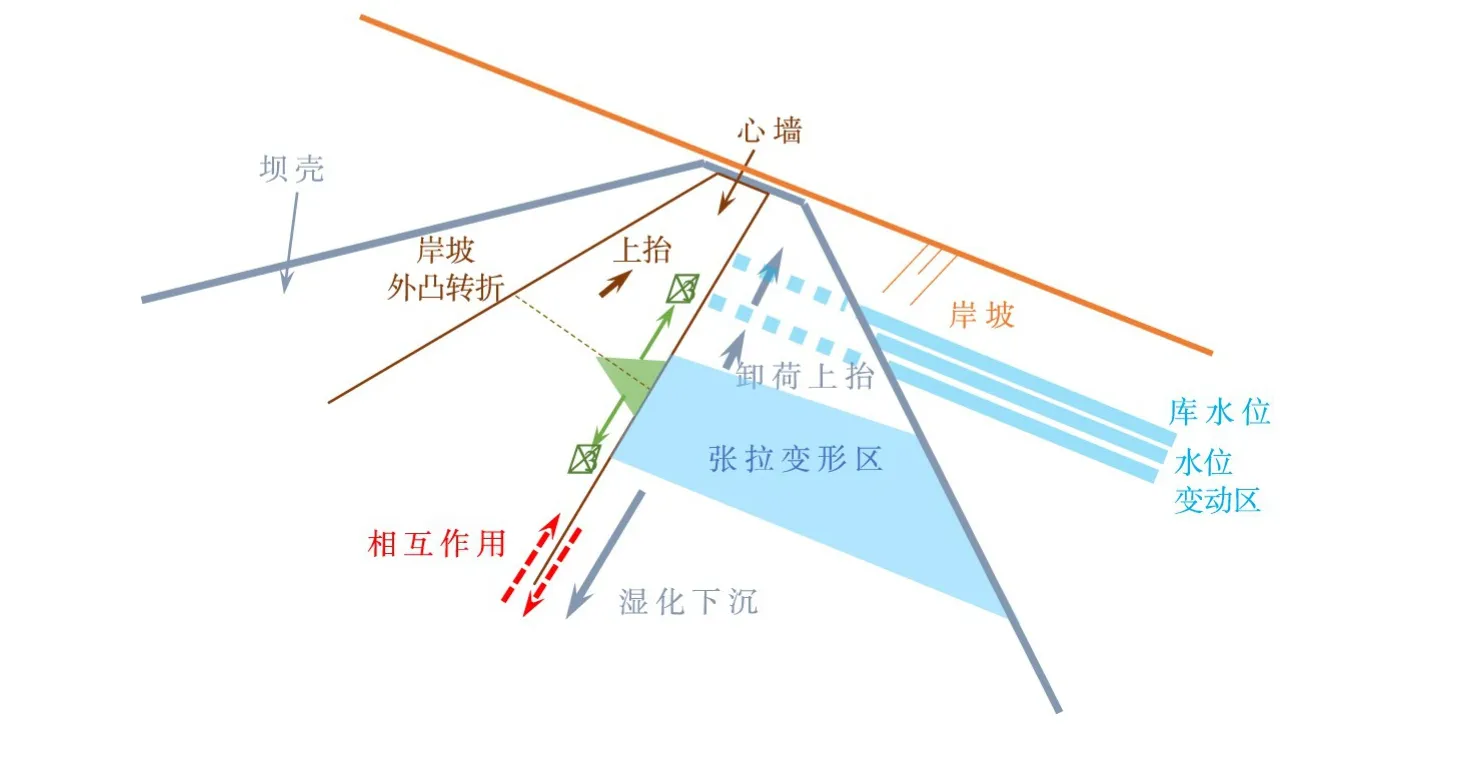
图2 坝壳湿化变形延时发生时库水位快速上升导致平行岸坡方向坝壳和心墙变形增量分布

如果岸坡的外凸转折位置靠近上述心墙集中拉伸带时，岸坡的约束作用可能放大下部沉降、上部抬升引起的心墙拉伸，导致心墙大、小主应力减小，小主应力小于孔隙水压力或库水压力。同样由于岸坡的约束作用，岸坡外凸转折位置的纵断面内应力可能转化为小主应力，其正交面穿过心墙，可以发生水力劈裂。可见，如果坝壳湿化变形延时发生、持续一定时间，则坝壳不同位置的浸水湿化变形、卸荷回弹变形分布，将使坝壳和心墙变形在空间和时序上出现不协调，心墙纵断面内特定方向应力成为小主应力并降低至小于库水压力，最终可能导致应力正交方向上出现水力劈裂［17］。

案例分析和理论分析说明，岸坡附近是较可能具备水力劈裂应力条件的位置。当考虑湿化变形时间发展时，心墙和坝壳的后期变形量值、发展速度及其空间分布的差异，与岸坡约束作用叠加，会大幅加剧坝壳与心墙在顺岸坡方向上的相互作用，导致顺岸坡方向变形不协调。岸坡存在外凸转折等特殊地形、水库快速蓄水可能加大变形不协调程度，引起心墙顺岸坡向局部拉伸、裂缝，并出现水力劈裂破坏。上述分析可能是心墙在初蓄过程中发生水力劈裂的机理。

较大的坝壳湿化变形及其随时间发展过程未在分析中得到充分考虑，可能是过去的分析中难以再现水力劈裂所需应力条件的主要原因。

3 初蓄水力劈裂破坏与湿化变形时间发展过程等关系的数值模拟

3.1 湿化变形时间发展过程的模拟 由于坝壳堆石料、砂砾石等粗粒土颗粒结构致密，即使试验室中采用的小粒径堆石料，吸水过程（即相对湿度或饱和度、总吸力、含水率等的变化）仍需相当时间［20］，如考虑浸水过程缩尺效应［21］，现场大粒径坝壳粗粒土的浸水变形持续时间可能更长。Oldecop和Alonso［22-23］考查了相对湿度变化时的堆石料变形发展规律，随总吸力减小、相对湿度增大，湿化变形逐步积累。也就是说，湿化变形存在随吸水过程发展的累积过程。

除粗粒土颗粒吸水过程所需时间外，相对湿度升高后保持不变的情况下湿化变形仍会持续。近期开展的侧限湿化试验［24-26］，证实了这种湿化变形时间发展过程的存在，张延亿等采用双曲线模拟这种时间发展过程；丁艳辉等进一步将湿化后变形划分为湿化瞬时变形和湿态流变变形，用流变表达这种湿化变形时间过程。

如果将湿化作用看做一种广义荷载［25］，湿化时间过程确与流变时间过程存在相似性。目前尚未见三轴湿化变形时间过程的报道，为验证分析湿化变形时间发展过程与水力劈裂现象之间的联系，根据既有三维湿化模型和流变模型的特点，本文建议了一种融合流变计算方法和湿化计算方法的湿化变形时间发展过程分析模型。上述模型构建方法已有学者开展过实践，在其开展的面板堆石坝湿化变形［27］分析中，引入了沈珠江流变模型中的指数函数［28］。

考虑对数曲线没有最终量的概念，且对数模型较易处理时间单位协调、解决室内试验变形量级与现场变形量级的差异等问题，同时与较多大坝实测沉降规律（后期变形随时间对数线性发展）接近，本文用作者提出的对数流变模型中类似函数［29-30］描述湿化变形发展过程（湿化变形随时间对数线性发展的规律也与既有湿化试验获得的变形发展过程较接近，如图3所示）。相应的湿化体应变εv-wetting和湿化剪应变γwetting随时间发展过程分别通过以下公式进行计算：

图3 试验湿化变形发展过程与对数模型的对比（试验数据引用自丁艳辉等［24］）

式中tw、tw0分别为浸水后时间和瞬时浸水变形参考时间，分析中采用相同时间单位即可，对时间单位的采用没有强制要求。对于土石坝计算，可按天（d）计，一般tw0可取0.1倍单位时间如0.1d。单位时间1 d时的湿化体应变εv-wetting和湿化剪应变γwetting，即分别等于浸水单位时间时体积湿化变形εvw10和浸水单位时间时剪切湿化变形γw10Cck（剪切湿化变形增加了系数Cck以提高模型灵活性和适用性）。对于湿化变形试验数据整理，时间单位可采用分（min）等。

假定全部湿化变形的应变主轴与应力主轴重合（暂不考虑湿化变形是否存在不重合性［25］），根据Prandtl-Reuss流动法则，将湿化变形分配至各应变分量：

式中：{εwetting}为湿化应变矢量；{I}为单位矢量；{s}为偏应力矢量。

模型中的浸水当天湿化变形量（体积湿化变形εvw10和剪切湿化变形γw10）采用李国英等的改进Cw-Dw湿化模型［31］计算，以考虑围压σ3、剪应力水平Sl等的影响，即

式中：Cw、Dw分别为体积应变湿化参数和偏应变湿化参数；nw为参数；Pa为1个标准大气压力，取100 kPa，用以调整公式量纲。模型假定湿化体积应变仅与围压有关、和剪应力水平无关，浸水湿化剪切应变仅与剪切应力水平相关、与围压无关。

3.2 考虑湿化变形时间发展时的水力劈裂破坏现象模拟 根据实际工程进行简化后建立的假想模型坝几何模型、有限元模型分别如图4和图5所示。模型坝高83.5 m，坝顶宽10 m，坝体上游侧坡比为 1∶2.0～1∶2.25，下游侧坡比1∶2.0。坝体分区主要包括心墙、坝壳堆石（及上游围堰）、上下游反滤等。心墙顶宽4 m，大坝靠近右侧坝头的88 m范围心墙上下游坡比为1∶0.4，该范围左侧30 m外区域的心墙坡比为1∶0.3，之间为过渡带。心墙两侧均设两层反滤，其中上游两层反滤宽度均为2 m，下游两层反滤分别宽2 m和3 m。

图4 计算几何模型

图5 计算有限元模型（右岸侧局部）

计算模型坝的填筑、蓄水过程以及各高程处蓄水速度如图6所示。假定的计算分析模型中心墙坡比（特别是右岸侧心墙坡比）相对较缓、宽度较大，坝壳堆石对心墙的拱效应较弱，能够更好与其他因素的作用进行区分。

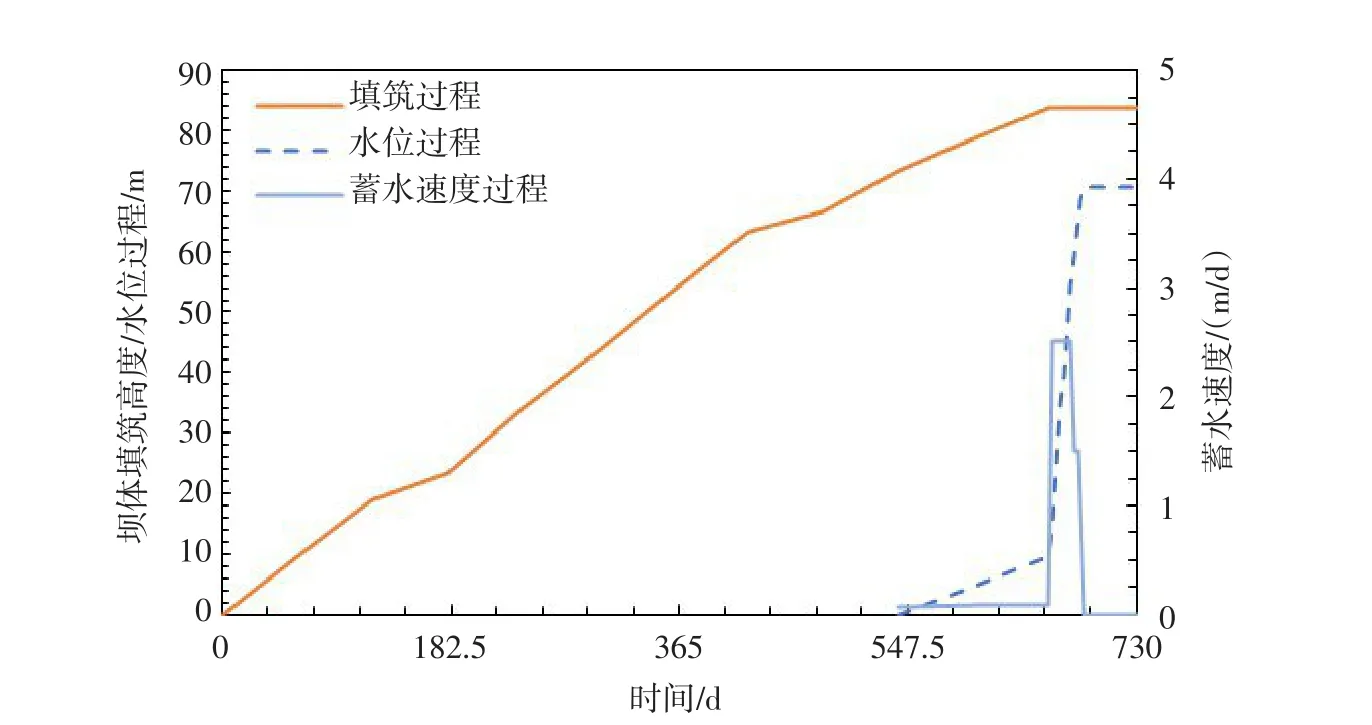
图6 计算模型坝填筑和蓄水过程

计算采用基于Biot固结理论的有效应力法进行，各筑坝材料瞬时应力变形采用邓肯EB模型，参数如表1。心墙渗透系数取7×10-6cm/s。

表1 各筑坝材料邓肯EB模型参数

坝壳湿化变形及其时间过程按3.1节所述模型进行计算，由于目前缺乏考虑粗粒料湿化变形时间过程的大型三轴试验成果，同时，即使室内大型三轴成果，也因尺寸效应等缘故，在湿化变形量值、时间发展速度等方面仍与现场存在较大差异，本分析中，仅为验证分析湿化变形时间发展过程与水力劈裂现象之间的联系，根据湿化和流变计算分析的经验，将参数Cw、Dw和nw确定为0.15、0.08和0.62。

从开始蓄水至水库满蓄（库水位距坝顶12.9 m）期间的坝体表面沉降增量（m）和顺河向水平位移增量（m）分布如图7所示。在水库蓄水过程中存在较大湿化变形时，坝壳出现整体下沉，增量最大值出现在坝体表面中上部；同时，上游坝面顶部附近有朝向上游侧的较大水平位移。

图7 蓄水过程中坝体表面位移增量分布（单位：m）

坝壳深部湿化变形的发展初期存在湿化变形增量高峰，而由于快速蓄水，库水位附近的浅层坝壳随有效围压减小而出现回弹变形，由于坝壳深部沉降增量和浅部向上变形的叠加，心墙因坝壳拖曳而在上部受到张拉，有效应力减小，这种有效应力减小现象存在基岩约束的岸坡侧更为明显，心墙上部部分位置有效小主应力出现负值，典型纵断面靠近右岸侧局部的有效小主应力分布如图8所示。由于岸坡凸变点的存在，凸变点处应力相对略高，但变坡点上、下侧近岸坡区域中心墙有效小主应力均为负值。

图8 典型纵断面上的有效小主应力分布（单位：MPa）

对于河谷中央大断面中的心墙或远离岸坡区域的心墙，大主应力一般沿竖向方向，中主应力多为纵断面中水平方向，小主应力则一般顺上下游方向。但是，由于岸坡约束的作用，心墙主应力方向多有一定旋转，在（平直）岸坡表面处，大主应力多顺岸坡方向，而其正交方向为中主应力或小主应力。当存在如本案例类似上缓下陡的岸坡凸变时，在凸变点以下、深度较大的位置，在高应力、大变形的作用与岸坡约束的联合作用下，心墙大主应力方向总体平行于岸坡，但方向明显缓于深部岸坡，似在深部岸坡平行方向上附加了部分上部缓岸坡的影响。但是，随着深度减小，靠近右岸岸坡部分的心墙有效大主应力方向并未朝向上部岸坡方向旋转，反而逐步沿逆时针方向旋转，并在跨过变坡点附近时有一定旋转角度突增，并在变坡点以上位置与岸坡保持较大夹角。心墙主应力迹线分布、有效大主应力方向与水平方向夹角分布分别如图9（a）和图9（b）所示。变坡点的存在，似乎导致心墙近岸坡侧变坡点上下区域出现了一定的“隔离”现象，因此，变坡点两侧特别是变坡点以下、靠近变坡点的区域出现了有效小主应力数值小于零的集中区域，这些区域内有效小主应力正交面的方向可以穿过心墙，出现了可以导致水力劈裂的应力条件。

图9 典型纵断面上的有效主应力迹线和有效大主应力方向与水平方向夹角分布

如将右岸突变基岩清除，岸坡基岩面按照一定坡度“一坡到底”，纵断面上的有效小主应力较存在突变情况下提高，不再存在负有效小主应力区域。

由此可见，当蓄水导致的湿化变形较大且随时间逐步增加时，叠加岸坡凸变等情况，可能使心墙因变形不协调而出现水力劈裂所需应力条件。

与“拉平”岸坡后水力劈裂应力条件消失的情况类似的是，保持其他因素不变，大幅提高蓄水速度或大幅减小蓄水速度，或不再考虑湿化变形时间发展（湿化变形浸水瞬时发生）、大幅加快湿化变形过程等，即使具有凸变岸坡的心墙，水力劈裂所需正交面贯穿心墙的负值有效小主应力条件仍难以再现。说明水力劈裂所需应力条件的产生，与不同位置处坝体变形增速存在密切的关系，仅有较为特定的湿化变形速度、蓄水速度等的组合才能导致水力劈裂。

4 结论与建议

本文采用数值模拟的方法，研究了坝壳湿化过程土质心墙坝初蓄水力劈裂问题，得到以下结论：坝壳被库水浸没后延时持续发展的湿化变形，与坝壳流变等后期变形叠加，导致库水位以下深部坝壳持续较大沉降变形增量；而库水位以下浅部水位变动范围内的坝壳因有效应力降低而出现向上变形增量。因坝壳深、浅部变形增量空间分布差异，心墙与坝壳变形不协调在不同部位出现差异，心墙在拖曳作用下出现中上部位置的顺岸坡方向拉伸。岸坡存在凸变等特殊地形、水库快速蓄水等可能加大变形不协调程度，引起心墙顺岸坡向局部拉伸、裂缝，出现纵断面内拉应力，其正交方向穿越心墙，从而产生水力劈裂破坏所需应力条件。

为了避免心墙水力劈裂的发生，提出如下几点建议：

（1）坝壳浸水湿化变形是深部坝壳变形增量主要成分之一，是顺岸坡方向后期变形不协调的主要来源之一。减小湿化变形等坝体后期变形可有效避免水力劈裂，应保证压实密度［32］，严格坝壳变形控制，以减小蓄水后湿化变形等后期变形。

（2）复杂岸坡条件如岸坡基岩凸变可能加剧其上下部分的心墙变形差异，宜将岸坡基岩面开挖为平直面或凹面，并在心墙与岸坡刚性接触面间布置柔性较高、变形适应性好的接触黏土区，尽量减小岸坡对心墙变形的约束。

（3）坝壳湿化变形存在一定的时间发展过程，湿化初期存在一定的变形增量发展高峰期，蓄水过快可能导致库水位以下水位变动区的上抬变形与深部较高速度的湿化变形增量叠加，导致心墙快速拉伸。在水库较低高程布置泄水构筑物，创造条件控制蓄水速度，或通过预测分析，选择与湿化速度耦合作用区间较为远离的水位变动速度（工程中一般难以提高水位上升速度，但存在降低水位上升速度的可能性），可防止快速蓄水过程中水位变动区上抬变形扩大顺岸坡方向变形不协调。