泥沙颗粒床面暴露度的理论分析及应用

张 磊，韩其为

（中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室， 北京 100048）

1 研究背景

泥沙颗粒在床面上的位置是影响泥沙运动的重要因素之一，在理论上如何给出合理的数学描述是学者们一直关注的核心问题。早在1950年Einstein在研究非均匀沙推移质输沙率时已引入表征隐蔽度的参数—隐蔽系数［1］，事实上已经反映了泥沙颗粒在床面上的位置对非均匀沙推移质运动的影响。后续随着研究的深入开展，韩其为等［2］提出了暴露度Δ的概念，其含义为从起动颗粒最低位置至与下游颗粒接触点之间的高差。暴露度与隐蔽度相比，虽然表示的含义相似，但暴露度更关注的是床面颗粒位置对泥沙起动及输移的影响。基于韩其为提出的暴露度概念，后续学者进一步分析了暴露度的分布形式，并将其引入到泥沙起动的分析中。近年来，杨文俊等［3-5］将泥沙颗粒从二维圆饼扩展到三维球体，提出了三维泥沙颗粒相对隐蔽度的概念和理论表达式；李林林等［6-7］分析了三维球体暴露度的分布规律；陈家萱等［8］和白玉川等［9］则是将垂向暴露度扩展到纵向暴露度，分析了双向暴露度对泥沙起动的影响。

此外，学者们聚焦于暴露度对非均匀沙起动流速的影响上［10-17］，其中，Egiazaroff［13］、秦荣昱和王崇浩［14］、陈媛儿和谢鉴衡［15］等学者通过床面不同粒径受水流的作用点高低不一致来反映流速的大小，同时采用隐蔽系数进行修正，但该种方法多数需要通过实验资料反算各种修正系数，带有一定的经验性；王涛等［16］、聂锐华等［17］通过引入等效粒径的概念对非均匀沙的起动进行了简化，其物理概念较明确，但其理论性有待商榷；冷魁和王明甫［18］以及孙志林和祝永康［19］等学者强调了不同粒径暴露度差别对泥沙起动的影响，建立了不同暴露度与起动流速的对应关系。总体来看，近年来对暴露度的研究取得了一定的进展，但在理论上的严谨性和系统性有待提高。另外，目前研究焦点只集中在床面泥沙起动上，对于暴露度对滚动、跳跃甚至推移质输沙率的影响涉及较少，需要对此开展系统研究。

本研究针对非均匀沙，提出了一个新的暴露度表达式，建立了暴露度与泥沙粒径的函数关系。在此基础上，分析了暴露度对非均匀沙滚动、跳跃运动参数以及推移质输沙率的影响。通过大量的实测资料对比分析，充分验证了公式的合理性，对暴露度对泥沙运动的影响机理形成了系统和深刻的认识。本文研究成果也是泥沙运动随机统计理论［20］的重要组成部分。

2 暴露度的理论表达式

韩其为和何明民在1965年于四川五通桥茫溪河野外水槽试验［21］中提出了暴露度的概念，但在应用中，相对暴露度Δ′更为方便，其定义为暴露度与床面泥沙粒径的比值，即

对于均匀沙，床面位置Δ′的分布在初步近似下可取为均匀分布，即其分布函数为［1］

式中：Δ′m为Δ′的最小值，对于均匀颗粒，其下三个颗粒紧密排列时Δ′m=0.134。对于非均匀沙，其分布情况较为复杂，近似地将其分为粗中细沙三个不同区间，分别给出了暴露度的表达式，即点分布和均匀分布［2］。

通过上述简单的公式形式建立起了非均匀沙暴露度与粒径之间的函数关系。但由于目前没有暴露度的直接观测数据，后续将通过推移质运动参数以及推移质输沙率等应用间接证明公式的合理性。

3 泥沙颗粒运动参数的计算

泥沙颗粒的运动具有随机性，它受水流底速Vb、床面位置Δ′以及粒径D等因素的影响。因此，在计算滚动与跳跃运动参数的期望值时，需要对上述参数进行积分，对于床面位置的影响，依据式（3）开展计算。

3.1 滚动运动参数 颗粒在床面的滚动是异常复杂的，为了能够探索其运动机理，需要将滚动过程进行简化，滚动形式简化为半接触滚动，即滚动速度较高，前半部与床面接触，后半部则颗粒可以脱离床面运动，竖向位移较小，可忽略。针对均衡滚动（即起点速度与落地终点速度相等），通过力学分析和求解，得到滚动颗粒运动速度的理论表达式为

图1 滚动运动时间与平均运动速度随Vb/ω0的变化

3.2 跃移运动参数 颗粒跃移运动可分为三个阶段，即颗粒由零上升至一个粒径D的高度、颗粒由一个粒径高度位置上升至最大高度和颗粒由最大高度下降至床面。在均衡跃移条件下，即颗粒跳跃的落地速度u3.x.3、u3.y.3与颗粒因碰撞而起跃前在床面的速度相等，这样可以推导出颗粒与床面碰撞后跃移的初始速度为

式中：u3.x为纵向速度；t3为跃移时间；u3.y.D为颗粒运动到一个粒径高的垂向速度；V1为由静起跳的临界速度。将颗粒容重γs、水流容重γ以及上述常数代入，并在给定的Δ′、条件下，即可进行迭代计算。为了与胡春宏等［22］的实测资料进行对比，分别计算了颗粒容重为1.043和2.65两种情况下的跃移距离和跃移高度，对比结果如图2和图3所示。其中底部作用流速Vf的计算表达式为：

图2 平均跳跃距离试验与理论的对比

图3 平均跳跃高度试验与理论的对比

3.3 推移质输沙率 围绕交换强度这一核心概念，严格推导了床面颗粒静止、滚动、跳跃、悬浮之间的转移强度，构建了转移概率矩阵，针对弱平衡和强平衡条件，可以得到不同的推移质输沙率公式。为了简化计算，主要对强平衡条件下的泥沙交换进行了计算。所谓强平衡，即由状态i转至状态j的强度（颗数）恰等于由该状态转来的强度（颗数），因此，根据床沙转为滚动的颗数与由滚动转为床沙的颗数相等，可以得到滚动输沙率的大小，即

式中：m0表示单颗泥沙的重量；P1.l为床面泥沙静止概率；Dl为非均匀沙时的分组粒径； μ2.l为颗粒滚动单步距离的倒数；t2.0.l为滚动时间，根据3.1节中的公式予以确定；ε0.l、ε1.l、ε2.0.l、ε4.l和βl为基本概率，分别表示不止动概率、起动概率、起跳概率、悬浮概率和起悬概率。类似地，针对跃移运动，根据床沙转为跃移的颗数与由跃移转为床沙的颗数相等，可以求得跃移输沙率：

式中：μ3.l为颗粒跃移单步距离x～3的倒数；t3.0.l为起跳时间，根据3.2节中的公式予以确定。式（15）和式（16）相加即为推移质输沙率，即

其中床面泥沙暴露度的影响包涵在公式中各个参数的确定过程中。为了验证公式的正确性，收集了大量的均匀沙和非均匀沙水槽试验数据，其中均匀沙的计算结果利用新厂站和襄阳站的实测资料进行了对比分析，如图4所示。从图中可以看出，两个测站的实测值均匀分布在理论曲线两侧，二者符合的较好，平均相对误差为-59.95%，对于推移质输沙率计算来说，该计算精度是可以接受的。

图4 新厂站和襄阳站推移质输沙率资料与理论结果的对比

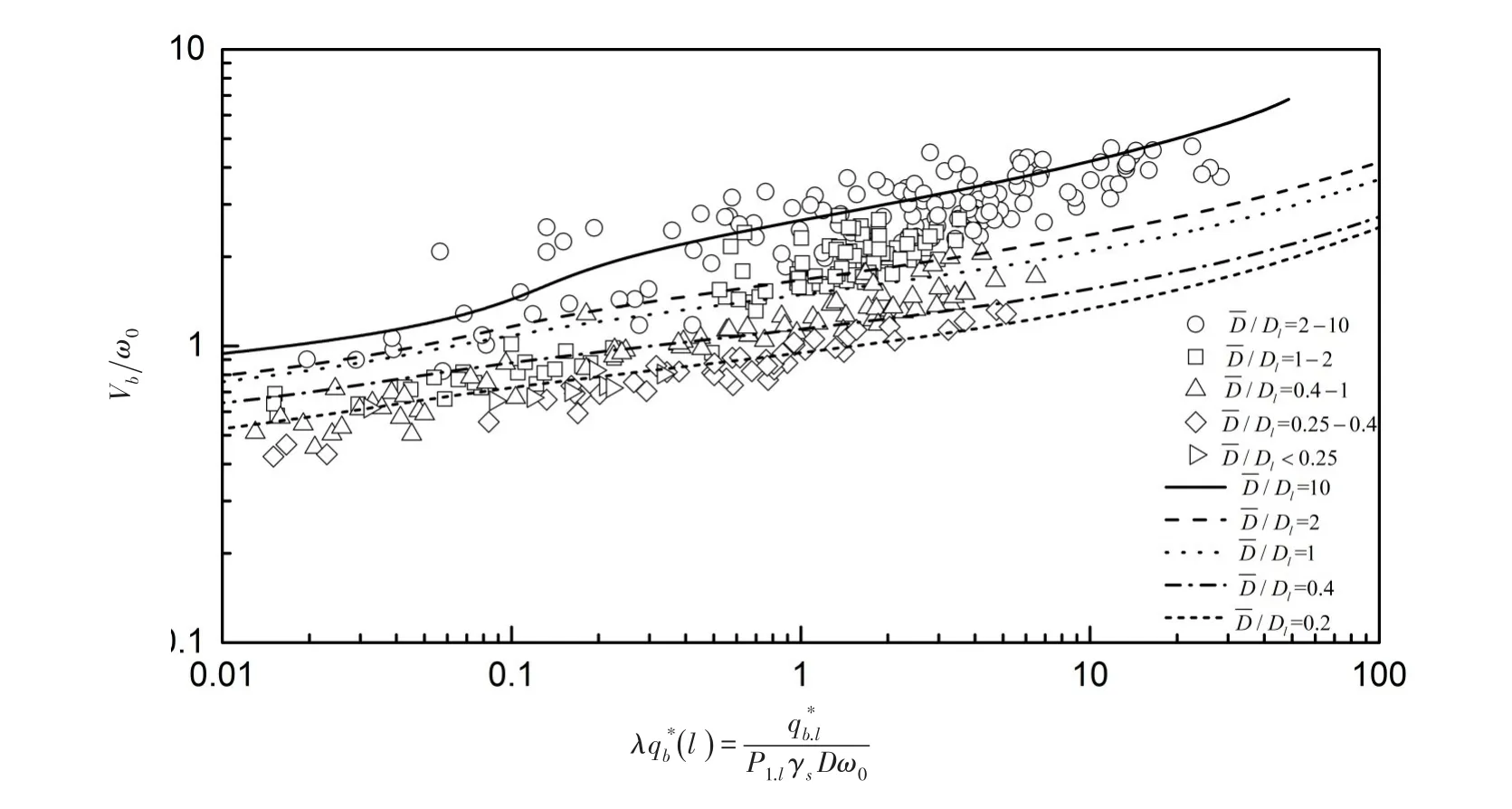
图5 Samaga实验资料与理论值的对比汇总结果

在分组输沙率验证的基础上，进一步计算了非均匀沙总输沙率的大小。无量纲化的总输沙率表达式为

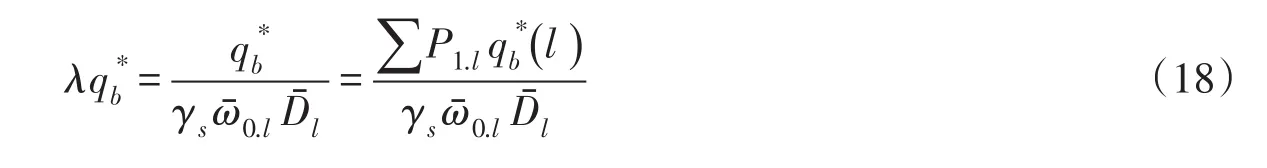
图6 Samaga不同中值粒径条件下非均匀沙总输沙率实测资料与理论值的对比

4 结论

床面泥沙暴露度是影响泥沙运动和输移的重要因素之一，本文围绕暴露度这一核心概念开展了系统的研究，得到结论如下：

（1）在已有成果的基础上，提出了一个新的非均匀沙床面暴露度计算公式，针对粗中细沙，分别建立了暴露度与泥沙粒径之间的函数关系，公式形式较为简单，便于在计算中应用。

（2）在公式提出的基础上，计算了单颗粒运动包括滚动和跃移运动参数的变化规律。结果表明，考虑了相对暴露度影响的滚动时间随着水流流速的增大，呈现先减小后略微增大的变化趋势；而平均滚动速度则是先增加后减小。针对跃移运动，利用跃移高度和跃移距离的实测数据对计算值进行了验证，二者基本符合良好。

（3）推导了滚动输沙率和跃移输沙率公式，进而得到了推移质输沙率公式。利用新厂站和襄阳站的实测资料，对均匀沙公式进行了验证，计算的平均相对误差为-59.95%，误差在可接受范围内；利用Samaga非均匀沙的实测资料，对非均匀沙分组输沙率和总输沙率均进行了验证，结果表明，分组输沙率计算值与实测值相吻合，总输沙率的计算值比实测值略微偏小，平均相对误差为-78.85%，这在推移质输沙率计算中也是可以接受的。