一种基于改进的LMS算法光纤信道自适应均衡器的研究*

王敬辉 孙守梅

1.天津现代职业技术学院智能工程学院 天津 300350；2.天津职业技术师范大学电子工程学院 天津 300222

引言

色散导致光纤中的光信号在传输过程中产生失真，并且这种失真会随着传输距离的增加越来越严重。其中多模色散、波导色散、材料色散和偏振模色散（PMD）是引起失真的主要原因。对数字光纤系统而言，色散造成光脉冲展宽导致前后脉冲相互重叠，引起数字信号的码间干扰（ISI），造成误码率增大。随着光纤通信系统传输速率的不断提高，色散成为制约高速光纤通信系统发展的主要因素。因此，对高速率、长距离的光纤通信系统必须考虑色散补偿问题，以消除ISI。

1 单模光纤信道的仿真模型

在理想信道中，发送滤波器和接收滤波器联合设计成在所需求的采样瞬时具有零ISI。即：

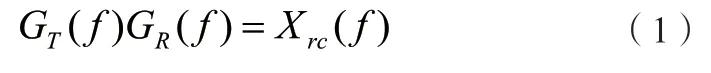
其中GT(f)为发送滤波器的频率响应，GR(f)为接收滤波器的频率响应，并且GR(f)为GT(f)的匹配滤波器，是升余弦频率响应特性，那么在采样时刻，ISI是零。然而，由于噪声和色散对实际的光纤信道产生影响，它并不是理想的。

即信道产生了失真，其中G(f)F为实际光纤信道传输函数。为了消除光纤色散引起的码间干扰，我们在接收端加一个自适应均衡器GE(f)，并且使：

系统仿真模型如图1所示，待发送数据经发送滤波器后进入光纤信道，再经采样后进入自适应均衡器，均衡器输出信号进入判决器，判决后输出，期望信号d(n)和均衡器输出信号) 进行比较，得到误差信号，以LMS自适应算法为准则调整均衡器抽头系数，实现自适应的均衡[1]。

图1 基于判决反馈结构的仿真框图

2 判决反馈均衡器和LMS算法

LMS算法一般采用递推的梯度（最陡下降）方法，用任意选择的可调节滤波器系数作为开始，然后将每一新的输入样本输入到这个自适应FIR滤波器，计算相应的输出，形成误差信号e(n)=d(n)-y(n)，并按方程

更新滤波器的系数，这里Δ 称作步长参数，x(n-k) 是输入信号在时间n上位于滤波器第k个抽头上的样本；而e(n)·x(n-k)是对第k个滤波器系数的一个梯度负值的近似估计，这就是为自适应的调节滤波器系数而使平方误差e2(n)之和ε达到最小的LMS递推算法。步长参数Δ 控制了达到最优解的算法收敛速率。传统LMS算法基于固定步长，大的Δ 步长值会导致大的步长调节，从而加速收敛；而小的Δ 步长值会产生较慢的收敛，然而，如果Δ 值取得太大，算法会变的不稳定。为了保证稳定性，Δ 必须选在下面的范围内

式中，N是自适应FIR滤波器的长度，Px是输入信号的功率。

本文提出了一种基于二分法的可变步长算法，使得步长随着迭代次数改变而改变。一开始步长较大，每次迭代步长变为原来的二分之一。这样既保证了收敛速度，又保证了收敛的稳定性和均衡效果最佳，使得Δ 同时满足公式（6）。

3 仿真结果

信道中加入指定信噪比的零均值高斯白噪声。图2（a）、（b）图是基于二分法的可变步长的LMS算法均衡前后的眼图，可以看出该算法也能有效的消除了码间干扰（ISI）。

图2 基于固定步长LMS和可变步长LMS算法的光纤信道均衡

其中（a）、（b）图是固定步长LMS和基于二分法可变步长的LMS算法的误差曲线。从两张图对比可以看出基于二分法可变步长的LMS算法有更快的收敛速度和更好的性能。固定步长LMS算法大概需要200多次迭代，而基于二分法可变补偿的LMS算法只需要大概50次迭代左右。

4 结束语

算法简单，易于实现是LMS算法的优点，缺点是收敛速度较慢，本文基于二分法可变步长LMS算法的提出有效解决了这个问题。使其更适用于对速度有更高要求的高速光纤信道均衡。