函数与导数的应用
一、单项选择题
1.(2020·成都为明学校高二月考)某产品的销售收入y1(万元)关于产量x(千台)的函数为y1=生产成本y2(万元)关于产量x(千台)的函数为(x>0),为使利润最大,应生产产品( )
A.9千台 B.8千台
C.7千台 D.6千台
2.(2020·安徽高三月考)从一张圆形铁板上剪下一个扇形,将其制成一个无底圆锥容器,当容器体积最大时,该扇形的圆心角是( )
3.(2020·辽宁高三月考)《蒙娜丽莎》是意大利文艺复兴时期画家达·芬奇创作的油画,现收藏于法国卢浮宫博物馆.该油画规格为,纵77cm,横53cm,油画挂在墙壁上的最低点处B离地面237cm(如图所示).有一
身高为175cm 的游客从正面观赏它(该游客头顶T到眼睛C的距离为15cm),设该游客离墙的距离为xcm,视角为θ.为使观赏视角θ最大,x应为( )

(第3题)
4.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图1所示).假定在水流量稳定的情况下,筒车上的每一个盛水筒都做逆时针匀速圆周运动,筒车转哗的中心O到水面的距离h为1.5m,筒车的半径r为2.5m,筒车每秒转动rad.如图2所示,盛水桶M在P0处距水面的距离为3m,则2s后盛水桶M到水面的距离近似为( )

(第4题)
A.3.2m B.3.4m
C.3.6m D.3.8m
二、多项选择题
5.(改编自2020·北京)为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改.设企业的污水排放量W与时间t的关系为W=f(t),用的大小评价在[a,b] 这段时间内企业污水治理能力的强弱.已知整改期内,甲、乙两企业的污水排放量与时间的关系如图所示.下列四个结论中正确的有( )
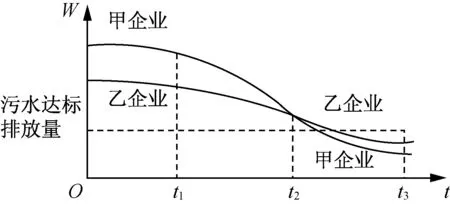
(第5题)
A.在[t1,t2)这段时间内,甲企业的污水治理能力比乙企业强
B.在t2时刻,甲、乙两企业的污水治理能力相同
C.在t3时刻,甲、乙两企业的污水排放量都已达标
D.甲企业在[0,t1),[t1,t2),[t2,t3]这三段时间中,在[0,t]
1 的污水治理能力最强
6.(2020·开原二中高三)国家统计局公布的全国夏粮生产数据显示,2020年国夏粮总产量达14281万吨,创历史新高.粮食储藏工作关系着军需民食,也关系着国家安全和社会稳定.某粮食加工企业设计了一种容积为63000π立方米的粮食储藏容器,已知该容器分上、下两部分,上部分是底面半径和高都为r(r≥10)米的圆锥,下部分是底面半径为r米、高为h米的圆柱,如图所示.经测算,圆锥的侧面每平方米的建造费用为元,圆柱的侧面、底面每平方米的建造费用为a元,设每个容器的制造总费用为y元,则下面说法正确的是( )
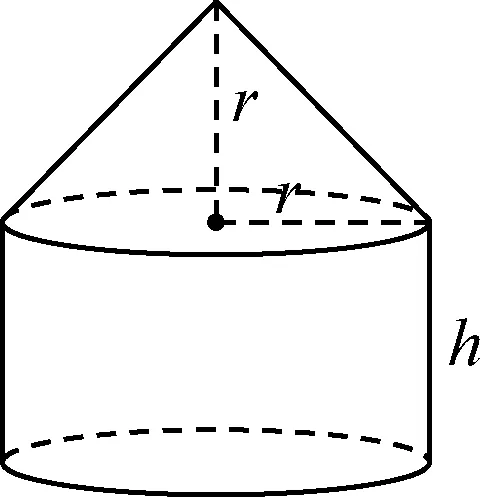
(第6题)
A.10≤r<40
B.h的最大值为
C.当r=21时,y=7029aπ
D.当r=30时,y有最小值,最小值为6300aπ
三、填空题
7.(2020·西南大学附中高三月考)为了研究口服某流感药物后人体血液中药物浓度随时间的变化规律,西南大学附属中学高三数学兴趣小组以本班同学为实验对象(被试).通过记录口服该流感药物x(h)时被试血液中药物浓度y(mg/mL)的方式获取试验数据.经多次实验发现,被试服用药物后,血液中药物浓度与时间成正比升高,当x=1h时药物浓度达到最高10mg/ml,此后,被试血液中药物浓度以每小时25%的比例下降.根据以上信息,从被试服用药物开始,其血液中药物浓度y(mg/ml)与时间x(h)之间的函数关系式为________.
四、解答题
8.(2020·上海交大附中高二期末)《九章算术》是古代中国乃至东方的第一部自成体系的数学专著,书本记载了一种名为“当甍”(音同“除萌”)的五面体(如图1).其中四边形ABCD为矩形,EF∥AB,△EAD和△FBC是三角形,“当甍”字面意思为茅草屋顶.图2是一栋农村别墅,为全新的混凝土结构.它由上部屋顶和下部主体两部分组成.如图3,屋顶五面体为“当甍”,其中前后两坡屋面ABEF和CDEF是全等的等腰梯形,左、右两坡屋面EAD和FBC是全等的三角形,点F在平面ABCD和BC上射影分别为H,M,已知HM=5米,BC=10米,梯形ABEF的面积是△FBC面积的2.2倍.设∠FMH=

(第10题)
(1)求屋顶面积S关于θ的函数关系式;
(2)已知上部屋顶造价由屋顶面积确定,造价为600元/平方米,下部主体造价由高度确定,造价为9600元/米.现欲造一栋上、下总高度为6米的别墅,试问:当θ为何值时,总造价最低?


