通信受限下基于终端滑模和指对数滑模方法的编队航天器姿态协同控制
易航 陈雪芹 刘明
0 引言
星间数据传输时,不可避免地存在通信时延[1].一般来说,星间数据传输时延[2-4]主要包括:1)排队延时:即待发送信息进入排队队列,到此信息开始发送所花费的时间;2)发送延时:从开始发送信息的第一个字节直至信息的最后一个字节所需的时间;3)传输延时:信息从发送设备传输到接收设备所花费的时间.以目前的技术手段,在进行星间通信的过程中是无法避免通信延迟问题的.如不考虑星间通信时延的影响,所设计的姿态协同控制律可能无法获得理想的控制性能,甚至会出现使姿态控制系统失稳[5]的情况.另一方面,在考虑通信时延的情形下,如采用基于事件触发的通信机制进行姿态协同控制器的设计,由于事件触发通信机制本身就会造成信息传输延迟,如再与上述的通信时延叠加到一起,无疑增加了控制器的设计负担和保守性,很难取得理想的控制性能[6-8].
除了事件触发通信机制以外,信号量化是另一种能够有效降低星间通信字节的手段[9].从自动控制理论角度来说,通信时延属于时间域上的信息滞后,而信号量化属于状态空间意义上的信息截取,如果一个控制系统同时存在通信时延和信号量化,其对应的信号误差,是可以通过合理设计控制器进行有效补偿的[10-13].基于这一原因,本文将针对编队航天器星间通信中的数据传输时延问题,采用信号量化的通信策略,研究对应的姿态协同控制器设计问题.
首先,在不考虑通信时延情形下,提出信号量化的星间数据传输策略,并基于终端滑模面技术设计一种姿态协同控制器以实现航天器编队姿态的渐近稳定;其次,在星间通信同时存在通信延迟和信号量化的条件下,提出指对数滑模面设计方法,构造了一种能保证编队航天器在有限时间内达到期望姿态的协同控制策略;最后,以包含4个刚体航天器的航天器编队为例,通过数值仿真验证了所提出的2种控制器方法的有效性.
1 问题描述
1.1 系统编队航天器姿态动力学、运动学方程
考虑包含n个刚体航天器的编队,第i个航天器(i=1,…,n)的动力学方程和基于修正的罗德里格参数(Modified Rodrigues Parameter,MRP)的运动学方程具有如下形式:
(1)
(2)

在上面的运动学方程中,注意到
因此F(σei)是一个满秩矩阵,其逆阵为
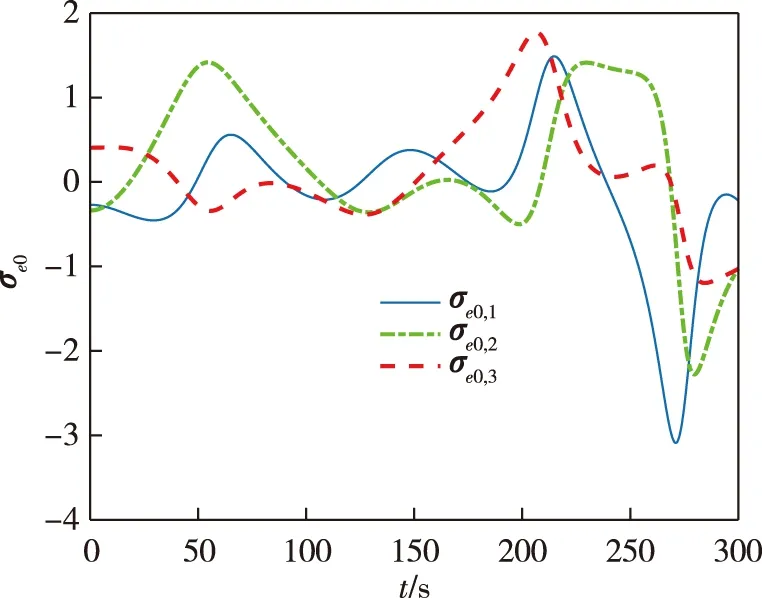
对于修正的罗德里格参数σei,其表达式如下:
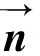
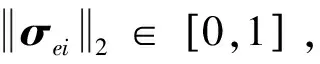
为了方便后续的分析和设计,对干扰力矩di做出如下合理假设:
假设2作用在编队航天器上的干扰力矩di(t)(i=1,2,…,n)满足如下范数有界条件:
其中dM>0是已知常数.
1.2 对数量化器
如前所述,航天器编队系统在进行姿态协同控制时,编队中各航天器间会发送、接收状态信息.为了减少通信压力、节约带宽,有时需要对状态信息进行量化处理,本节采用对数量化策略对星间通信数据进行信号量化.
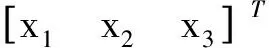
(3)
其中参数xj=ρ1-jx0(j=1,2,…),x0>0是事先给定的量化器初始值,0<ρ<1表示对数量化器密度,δ=(1-ρ)/(1+ρ).ρ和δ刻画了量化器的量化稠密程度:ρ越小,δ越大,量化密度越大,量化越稀疏;ρ越大,δ越小,量化密度越小,量化越密集.图1是一个对数量化器的例子,其中δ=1/3,ρ=0.5,x0=0.001.从图1中可以看出ρ决定了量化区间大小,因此可以根据实际情况调节ρ和δ的数值以得到理想的对数量化器.

图1 量化函数Fig.1 Quantization function
引理1给定一个向量x∈R3,若采用对数量化器(3)对x进行量化,定义量化误差dq(x)=Q(x)-x,则dq(x)满足如下的约束:
证明由对数量化器(3)的性质可知,当xi≤x0/(1+δ)时,Q(x)=0,因此,根据矩阵1-范数的定义可以推出
|dq(x)|=|Q(x)-x|=|x|≤
(4)
成立.而当xi>x0/(1+δ)时,则有
成立.注意到式(4)中的xj就是xi的量化值Q(xi),因此对应的量化误差dq(x)满足:
另一方面,由δ∈(0,1)的性质可知其满足δ/(1+δ)<δ/(1-δ),因此,当xi>x0/(1+δ)时量化误差dq(x)的范数满足:
综合xi>x0/(1+δ)和xi≤x0/(1+δ)两种情况考虑,对任意的向量x∈R3,其量化误差dq(x)一定满足如下约束:
2 通信时延和信号量化情形下航天器编队协同控制器设计
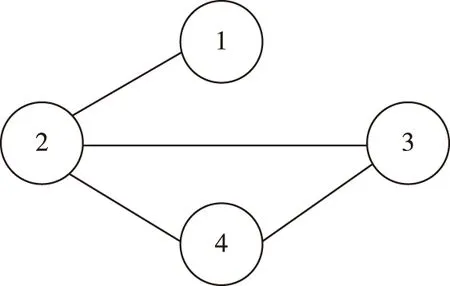
本节将针对存在通信时延和信号量化情形,设计姿态协同控制器使航天器编队完成给定的姿态跟踪任务.在编队飞行过程中,为实现姿态协同目标,第i个成员航天器需要第j个成员航天器的姿态信息(σej和ωej).因此,为方便下面分析,把和第i颗成员航天器有信息通信的所有其他成员航天器定义为一个集合Ni.
假设3定义第i个航天器和第j个航天器间的通信延时Tij>0是固定的常数,并且满足Tij=Tji.在进行本节的航天器编队姿态协同控制器分析和设计工作之前,需要给出下面两个关于系统有限时间收敛的引理.
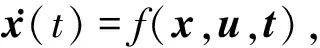
其中,a>0,b>0,λ∈(0,1)为已知常数,则该非线性系统是有限时间稳定的,且收敛时间Treach满足:
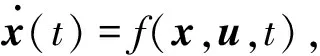
其中,b>0,λ∈(0,1)为已知常数,则存在一个集合U0⊂Rn,使对任意的初始条件V(x0)∈U0⊂Rn,都能保证该非线性系统是有限时间稳定的,且收敛时间满足:
2.1 终端滑模姿态协同控制器设计
本小节首先考虑理想的星间通信情形,即编队航天器的星间通信不存在时延,采用信号量化通信策略进行航天器编队姿态协同控制器的分析和设计,以期在实现编队航天器姿态协同任务的同时,节省编队航天器之间的通信字节和带宽.
首先,针对编队航天器姿态控制系统(1)—(2)定义如下所示的终端滑模面:
(5)
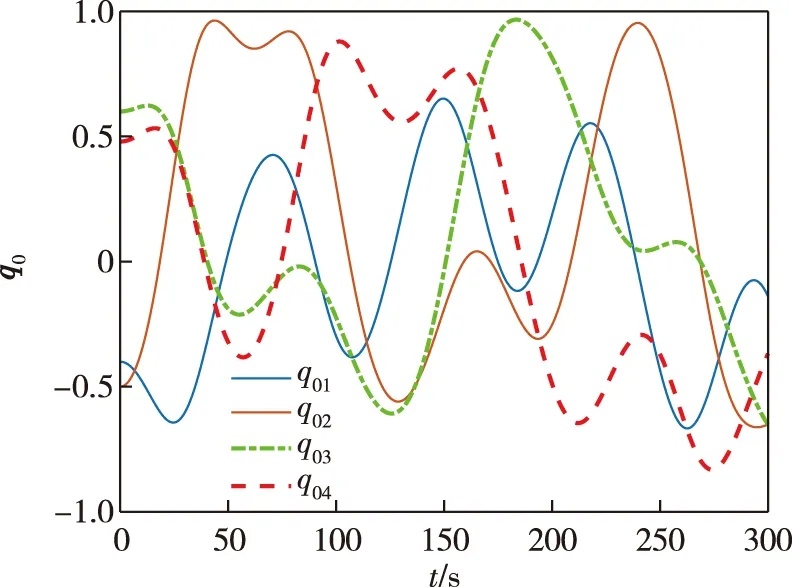
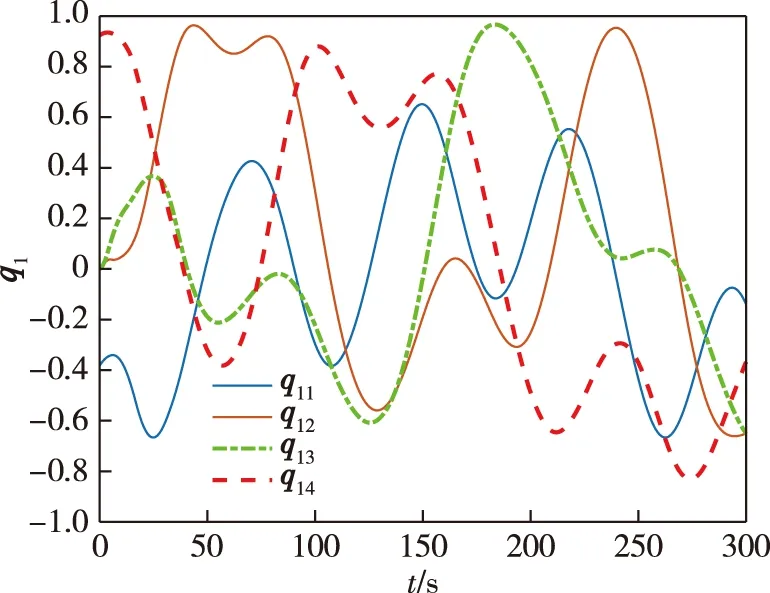
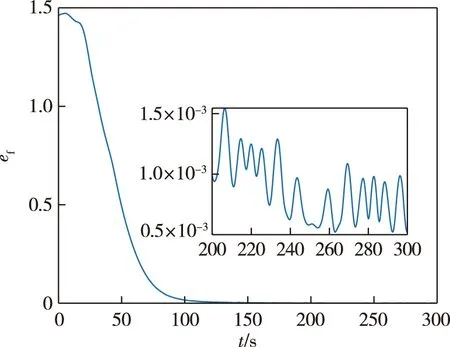
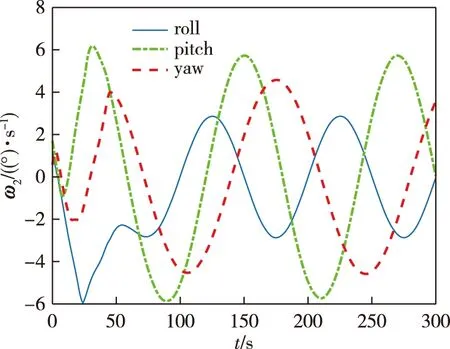
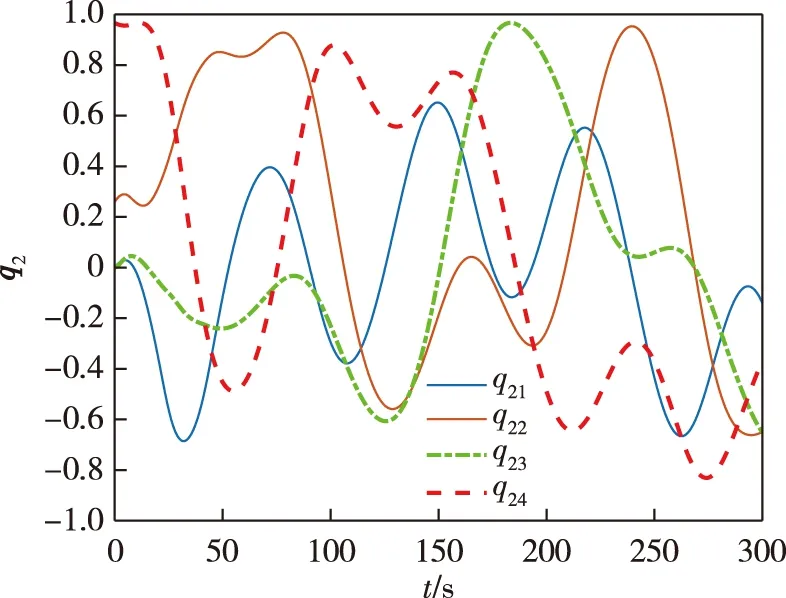
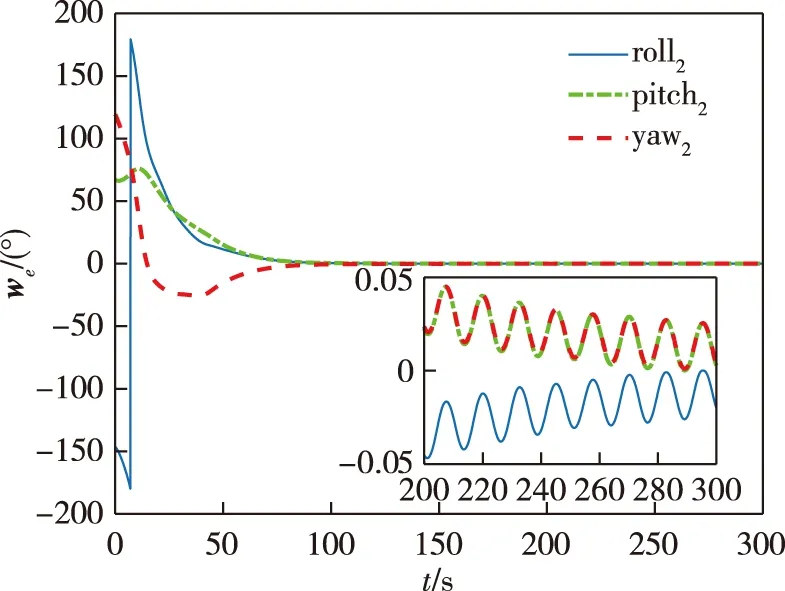
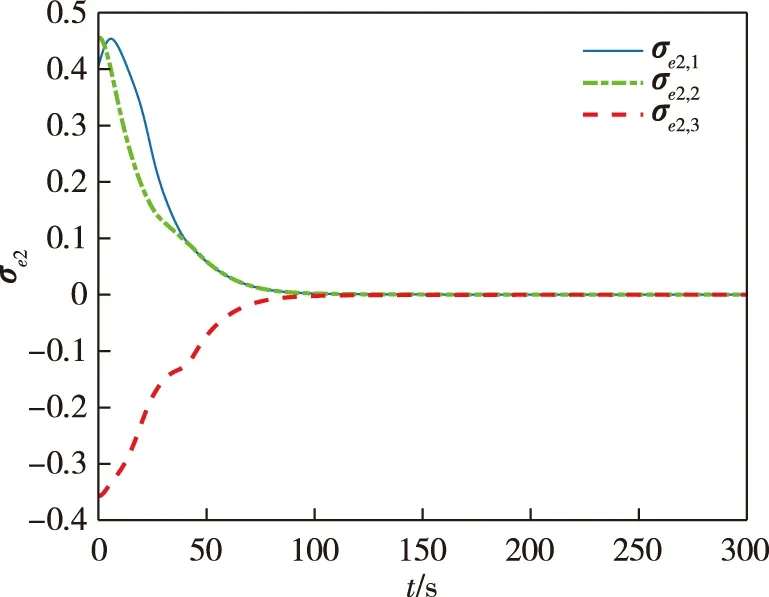
其中c>0,1 当编队航天器姿态控制系统(1)—(2)的状态轨线到达滑模面si=0上后,由滑模面函数(5)可以推出 (6) 引理4当编队航天器姿态控制系统(1)—(2)的状态轨线到达滑模面si(t)=0之后,其姿态参数σei(t)和ωei(t) 将在有限时间内收敛到原点,并且收敛时间t1满足: 证明对编队航天器姿态控制系统(1)—(2) 定义如下的Lypaunov函数: 对W(t)求导,并将(6)代入可得: (7) 由于参数d满足1 (8) 将(8)代入(7)可以推出: 可改写为 另一方面,当σei=0时,姿态运动学方程(1) 退化为 说明航天器角速度矢量ωei也将在有限时间内收敛到平衡点. 引理4说明当编队航天器姿态控制系统(1)—(2) 的状态轨线到达滑模面si(t)=0后,σei和ωei将在有限时间内收敛到原点.下面来分析滑模面si(t)=0的能达性.注意滑模函数si(t)时间导数为 (9) 另一方面,由编队航天器姿态动力学系统(2)可以推出: 将上式代入(9)得到: (10) 定理1考虑编队航天器姿态控制系统(1)—(2),并将其中各成员航天器的控制力矩设计为如下形式: (11) 其中滑模控制器增益设计为 则在控制律(11)作用下,编队航天器姿态控制系统(1)—(2) 的状态轨线将在有限时间内达到滑模面si(t)=0. 证明对编队航天器姿态控制系统(1)—(2)定义如下Lypaunov函数: 将姿态协同控制律(11)代入滑模面方程(10)可得: (12) (13) 将不等式(13)代入Lypaunov函数V(t)的导数(12)可得: (14) 考虑不等式(14)的最后一行,第一项满足如下性质: (15) 同时,第二项满足 (16) 其中 将式(15) 、(16)代入不等式(14)得到 并进一步改写为如下形式: (17) 考虑不等式(17),并基于引理2可推断出编队航天器姿态控制系统(1)—(2)的状态轨线将在有限时间内达到滑模面si(t)=0上. 上一小节针对理想的星间通信情形,采用信号量化通信策略进行了航天器编队姿态协同控制器的分析和设计.本小节将考虑航天器编队中星间信息传输的通信延迟现象.基于信号量化传输策略并采用指对数型滑模面理论设计对应的姿态协同控制器,以保证编队航天器能够完成姿态协同任务. 首先,定义如下形式的指对数滑模面函数: si2(t)=ωei(t)+F-1(σei)[αA(σei)+βB(σei)], (18) 其中参数矩阵A(σei)和B(σei)具有如下形式: α>0,β>0是待设计常数,q>0,p>0要求选取为奇数并且满足q 考虑指对数滑模面方程(18),当si2(t)=0时该方程退化为 (19) 针对系统(19),给出如下引理. 引理5当编队航天器姿态控制系统(1)—(2)的状态轨线到达si2(t)=0之后,姿态参数σei和ωei将在有限时间内收敛到平衡点,并且收敛时间满足: 证明对编队航天器姿态控制系统(1)—(2)构造如下Lypaunov函数: 对其求导得: 当编队航天器姿态控制系统(1)—(2) 的状态轨线到达si2(t)=0之后,显然满足方程(19).将其代入上式得到: ln(2-e-|σei1|)sign(σei,j)- 因此推出 当σei(t)=0之后,根据方程(19) 可知角速度误差满足: ωei=-F-1(σei)[α·0+β·0]=0, 这意味着在t2时刻ωei也收敛到了平衡点.证毕. 下面再来分析滑模面si2(t)=0的能达性.考虑指对数滑模面函数(18),可推导出其导数方程为 (20) (21) 将编队航天器的姿态动力学方程(2)代入(20)可以推出: (22) 下面给出关于保证指对数滑模面函数(18) 能达性的定理. 定理2考虑指对数滑模面方程(20),将编队航天器姿态控制系统中各成员航天器的控制力矩设计为如下形式: (23) 证明对编队航天器姿态控制系统(1)—(2) 定义如下的Lypaunov函数: (24) 则对其求导得到 (25) 在式(25)中,注意到如下性质成立: 2si2,2sj2,2(t-Tij)+2si2,3sj2,3(t-Tij)= 因此(25)可以放大为 (26) 又因为如下性质成立: 因此可以进一步推出: (27) 基于滑模面方程(22),并将控制律(23)代入式(27)得到: (28) 显然,指对数滑模面si2(t)=0是渐近能达的,即编队航天器姿态控制系统(1)—(2)的状态轨线将渐近收敛到滑模面si2(t)=0上. 本节将给出数值仿真算例,验证所提出的两种编队航天器姿态协同控制器设计方法的有效性.假设整个航天器编队包含4个成员航天器和1个虚拟的领航航天器,并且领航航天器的姿态参数按如下公式计算: 其中各个参数的初始值设置为 通过单位四元数和修正罗德里格参数之间的转换公式可以进一步求出领航航天器姿态的修正罗德里格参数表示: 图2—4 分别给出了领航航天器的姿态角速度、姿态四元数及对应修正罗德里格参数随时间的变化曲线. 图2 领航航天器的角速度变化曲线Fig.2 Trajectory of w(t) for leader spacecraft 图3 领航航天器的姿态角q(t)变化曲线Fig.3 Trajectory of q(t) for leader spacecraft 图4 领航航天器的修正罗德里格斯参数信息Fig.4 Trajectory of MRP for leader spacecraft 4个成员航天器的转动惯量矩阵设置为如下形式: 4个成员航天器的初始姿态角速度设置为 作用在各成员航天器上的干扰力矩为 各成员航天器的初始姿态四元数为 此外,各成员航天器间通信情况如图5所示. 图5 成员航天器间的通信拓扑Fig.5 Communication topology of member spacecrafts 为了合理地描述编队协同控制器的性能,针对编队航天器定义如下的状态保持度函数es(t)及编队保持度函数ef(t): 此外,考虑1号成员航天器,其参数变化曲线如图8—13所示.可以看出,1号成员航天器的姿态误差在300 s内快速收敛,同时超调较小,控制力矩曲线变化平滑,符合工程中的实际要求.另外,虽然1号成员航天器的角速度误差没有实现渐近稳定,但其精度也在合理范围内. 图9 成员航天器1的姿态角q(t)变化曲线Fig.9 Trajectory of q(t) for member spacecraft 1 图10 成员航天器1的修正罗德里格斯参数信息Fig.10 Trajectory of MRP for member spacecraft 1 图11 成员航天器1的控制器输入扭矩信息Fig.11 Trajectory of controller torque for member spacecraft 1 图12 成员航天器1的角速度误差变化曲线Fig.12 Trajectory of we(t) for member spacecraft 1 图13 成员航天器1的姿态误差变化曲线Fig.13 Trajectory of σe(t) for member spacecraft 1 本节通过仿真验证2.2节提出的控制器的控制性能.相关仿真参数选取如下:仿真时间设置为300 s,采样时间间隔为0.1 s,通信时延为0.1 s;量化器(3)的参数设置为x0=0.000 1,ρ=0.5,δ=1/3;姿态协同控制器(23)的相关参数设置为α=0.015,β=0.03,p=5,q=3,kp=2.5 .仿真结果如图14—21 所示.其中航天器编队的状态保持度es(t)变化曲线和编队保持度ef(t)变化曲线分别如图14和图15所示.可以看出,在控制器(23)的作用下,编队航天器的状态保持度和编队保持度是渐近稳定的. 此外,2号成员航天器的参数变化曲线如图16—21 所示.可以看出,2号航天器的姿态误差也具有快速收敛、超调较小、控制力矩曲线变化平滑以及易于实现等优点,但是和上一小节的仿真结果相比,本小节中2号航天器的姿态误差的收敛速度稍微慢一些.这个现象和两种控制器(控制器(11)和控制器(23))中滑模面函数的结构不同有关. 图14 航天器编队的状态保持度变化曲线(控制器2)Fig.14 Trajectory of es(t) for spacecraft formation under controller 2 图15 航天器编队的编队保持度变化曲线(控制器2)Fig.15 The trajectory of ef(t) for spacecraft formation under controller 2 图16 成员航天器2的角速度变化曲线Fig.16 Trajectory of w(t) for member spacecraft 2 图17 成员航天器2的姿态角q(t)变化曲线Fig.17 Trajectory of q(t) for member spacecraft 2 图18 成员航天器2的修正罗德里格斯参数信息Fig.18 Trajectory of MRP for member spacecraft 2 图19 成员航天器2的控制器输入扭矩信息Fig.19 Trajectory of u(t) for member spacecraft 2 图20 成员航天器2的角速度误差变化曲线Fig.20 Trajectory of we(t) for member spacecraft 2 图21 成员航天器2的姿态误差变化曲线Fig.21 Trajectory of σe(t) for member spacecraft 2 本文研究了存在通信时延情形下基于信号量化策略的编队航天器协同控制问题,分别采用终端滑模面、指对数滑模面设计了编队航天器姿态协同控制器,保证编队航天器能够在有限时间内达到期望的姿态协同.未来工作将关注于挠性航天器编队以及有向通信拓扑情形下的编队航天器姿态协同控制问题.
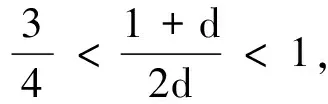
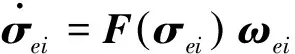
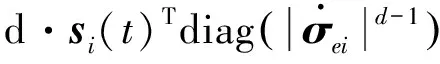
2.2 基于指对数滑模面的姿态控制策略
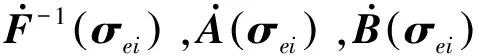
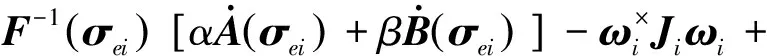
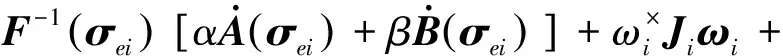

3 仿真算例

3.1 存在信号量化时的控制器设计
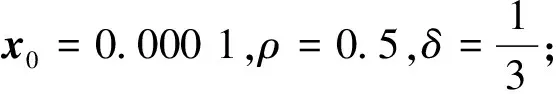
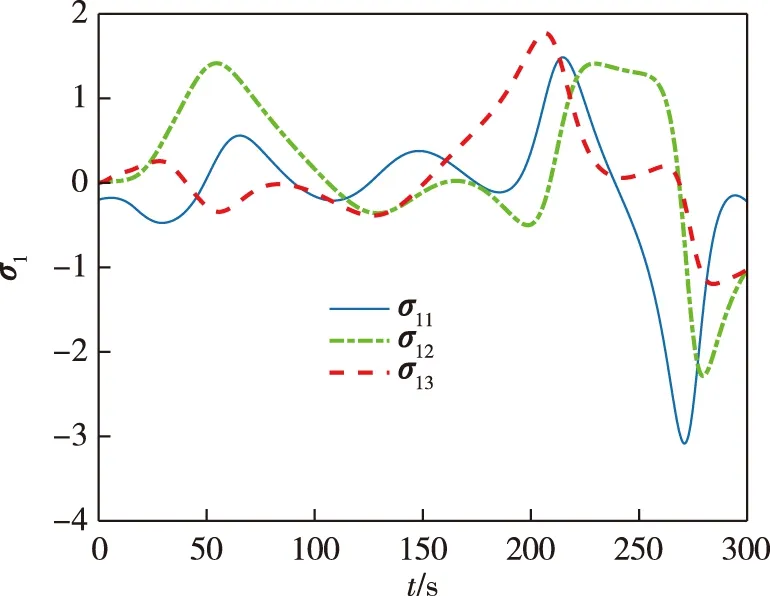
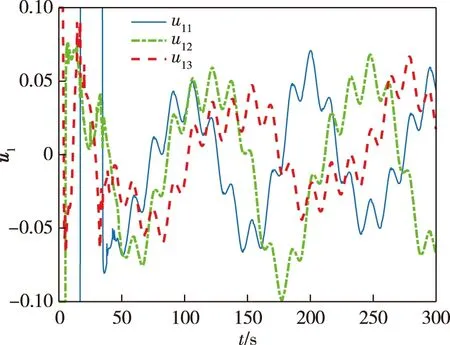


3.2 存在通信时延和信号量化时的控制器设计



4 结论

