智能船舶自动舵系统自适应模糊输出反馈控制
朱丽燕 李铁山,2
0 引言
自动舵是智能船舶最重要的操控系统之一,在船舶的航行安全、能源成本和船员的劳动强度等方面起着重要的作用.智能船舶运动具有大时滞、大惯性、强非线性等特点,同时由于航行条件变化和环境干扰等问题使得船舶运动模型具有严重的不确定性.因此,自动舵算法设计,即智能船舶航向控制,成为船舶控制领域中的难点和热点问题[1-2]. 近年来,智能船舶航向控制研究取得了丰富的成果[3-5]. 现有大多数研究基于状态反馈方法,即控制设计所需的系统状态信息全部已知.船舶航行中,载况、航速和外扰等变化不仅会带来模型不确定性问题,同时还给传感器量测造成困难,再加上传感器本身存在测量噪声,将带来某些状态信息不可测问题,如自动舵系统仅能测量航向角信息,而很难得到回转角速度信息,这时应引入状态观测器来获得控制器设计时所需要的回转角速度信息[6].此外,智能船舶的自动舵系统存在输入饱和现象,而且饱和非线性问题在控制器设计时是不可避免的,主要表现为舵角受限,这就意味着控制器设计时需要补偿输入饱和带来的信号不匹配问题.为减少频繁的无效操舵导致舵机过度磨损和能量耗费,应引入辅助系统解决舵角受限问题[7].
智能船舶在特殊海域航行时,航向追踪任务对追踪精度具有一定要求,需要达到指定性能.建立误差转换系统,可以对系统输出航向与参考信号的追踪误差进行一定的约束变换,从而提高智能船舶的控制精度,因此,自动舵系统的控制器设计还应考虑系统的指定性能问题.文献[8]解决了具有指定性能的水面舰艇跟踪控制问题;文献[9]基于误差变换函数,将水面舰艇的约束跟踪控制转化为无约束系统的镇定问题,但跟踪时间过长,并缺乏对船舶航向实际性能需求的考虑.
本文研究了智能船舶自动舵系统控制问题,利用航向跟踪误差设计误差转换系统,并定义辅助系统对受限舵角进行补偿.利用模糊逻辑系统对未知函数进行逼近,设计状态观测器,从而得到未知回转角速度的估计信号.采用动态面技术,得到虚拟控制函数的一阶滤波器,将转换误差、辅助系统、状态观测器应用于控制器设计,不仅能够实现航向追踪任务,同时解决了实际工程中舵角幅值限制问题,提高控制精度.
1 问题描述
1.1 数学模型
考虑船舶稳态回转非线性特性,本文采用如下船舶航向非线性系统数学模型[10]:
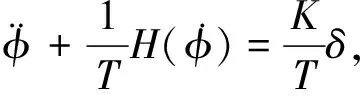
(1)

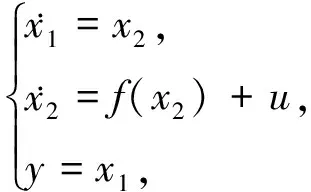
(2)

1.2 饱和模型
为使系统的控制性和稳定性能够得以保证,在控制器设计中考虑舵角输入饱和限制(一般幅值是35°),式(2)可以被改写为
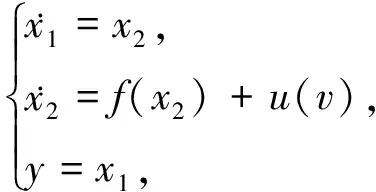
(3)
其中,v是待设计控制信号,u(v)是受饱和约束的执行器输入信号,u(v)可被描述为

(4)
其中,uM是舵角的最大幅值,系统的饱和特性可被光滑函数逼近为

(5)
sat(v(t))可被表述为

(6)
其中,ρ(v)=sat(v)-h(v)是一个有界的函数,其有界性可被表述为
|ρ(v)|=|sat(v)-h(v)|≤uM(1-tanh(1))=S1.
(7)
当|v|在0与uM之间变化时,ρ(v)的值由0增加到S1,当|v|超出变化区间,ρ(v)由S1减少到0.
1.3 指定性能
智能船舶自动舵实现航向追踪控制,要求船舶保持给定航向航行,当船舶在特殊海域航行时,对航向追踪性能及追踪精度有一定的要求.从自动舵设计角度来说,对于给定的参考信号,所设计的控制器可以使智能船舶的航向角的追踪误差达到指定的性能.本文将指定性能[11-12]描述为如下不等式:
-ωminμ(t)
(8)
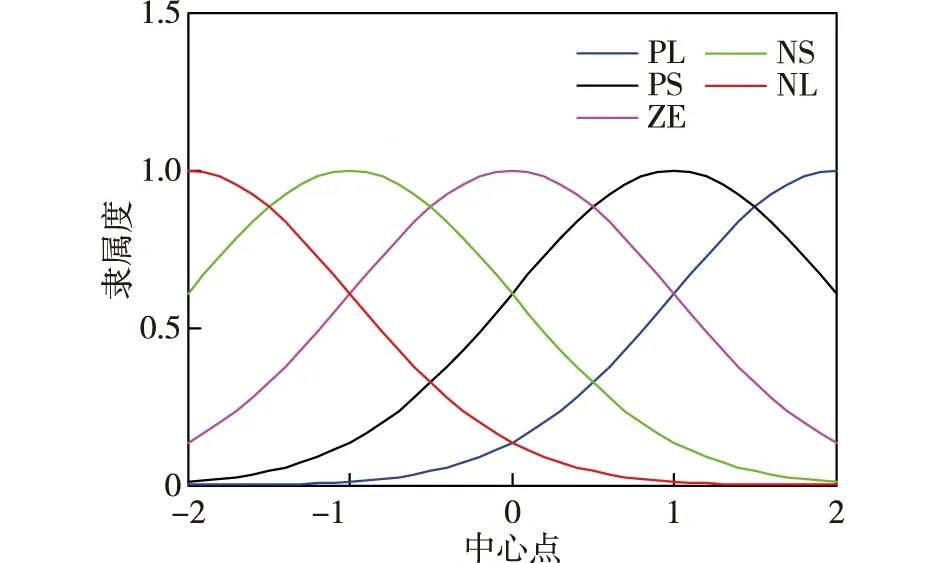
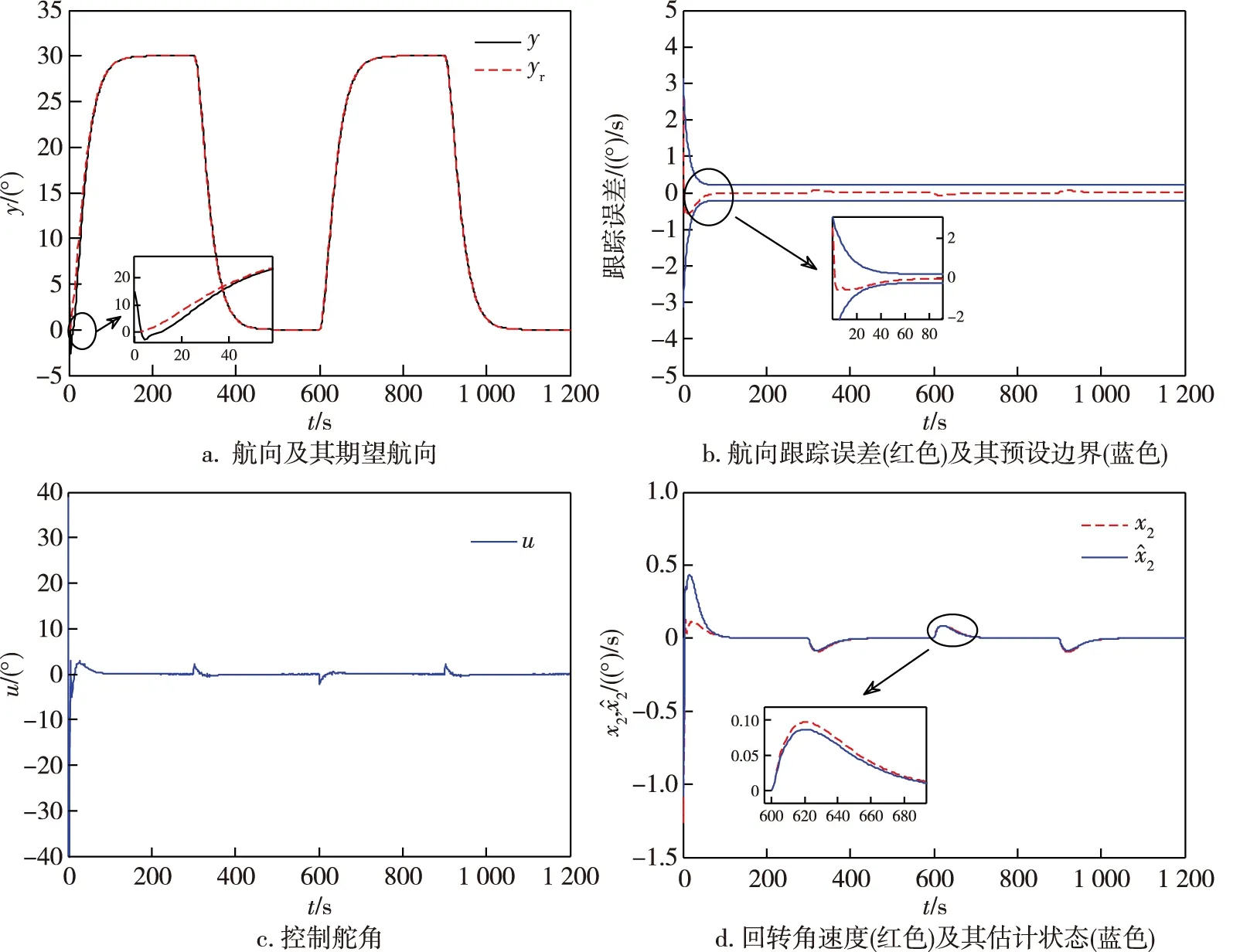
其中,μ(t)=(μ0-μ∞)e-at+μ∞,ωmin,ωmax,a和μ∞是设计参数,μ0=μ(0),选择μ0使μ0>μ∞,不等式-ωminμ(0) 引理1[13]f(x)是定义在闭集Ω内的连续函数,对任意给定的常数ε>0,存在一个模糊逻辑系统θTφ(x)使得 (9) 实际应用中的很多工况下,智能船舶自动舵系统的回转角速度是不可获得的,可以引入状态观测器来对其进行估计.在本文系统(3)中,唯一可测的状态信息是y=x1,设计状态观测器来对未知航向角信息进行估计. 设计状态观测器 (10) 改写式(10)得 (11) 选取向量M,A为严格的Hurwitz矩阵,因此,给定矩阵Q=QT>0,存在矩阵P=PT>0满足: ATP+PΑ=-Q. (12) (13) (14) 式中,ε为估计误差. (15) (16) 利用杨氏不等式可得: (17) (18) (19) (20) 将式(17)—(20)代入式(16)得: (21) 其中, 对于系统(3),设计自适应模糊输出反馈指定性能控制器,取误差变换系统为 (22) 其中,z2是虚拟误差面,r是状态变量,α1是虚拟控制函数,χ是关于r和α1的误差变量,ξ是辅助信号,其系统动态为 (23) 为实现式(8),将受约束的追踪误差通过不受限不等式进行转换[11],定义 s(t)=μ(t)H(ζ(t)),∀t>0, (24) 其中,ζ是转换后的误差变量,H(ζ)是预设函数,具体为H(ζ)=(ωmaxeζ-ωmine-ζ)/(eζ+e-ζ).易得:∂H/∂ζ=2(ωmax+ωmin)/(eζ+e-ζ)2>0.由H(ζ)的定义和式(24)可得: (25) (26) 定义如下状态变换: (27) 易得 (28) 若z1(t)是有界的,则式(22)中的s1是满足指定性能的[12].基于后推方法,针对智能船舶自动舵系统,控制器设计及系统稳定性分析过程如下: (29) 选取李雅普诺夫函数V1为 (30) 由式(13),(21),(22)和(30),有 (31) 由杨氏不等式可得: (32) 将式(32)代入式(31),则 (33) 设计虚拟控制函数α1为 (34) 其中,c1>0是待设计参数. 将式(34)代入式(33),则 (35) 为避免对虚拟控制函数α1重复求导,定义一阶滤波器为 (36) 其中,τ>0是待设计参数. 由式(22)可得: (37) 其中,Y(·)是连续的非线性函数. 步骤2.由式(10)、式(22)和式(23)得 (38) 选取李雅普诺夫函数 (39) 由式(22),(29),(35),(38)和(39),有 (40) 由杨氏不等式可得: (41) 将式(41)代入(40)可得: (42) 设计控制器和参数自适应率分别为 (43) (44) 其中,c2>0,γ>0,σ>0是待设计参数. 根据式(15),(39)和(40),并将式(43)和式(44)代入(42),有 (45) 由杨氏不等式可得: (46) (47) 将式(46)和式(47)代入式(45),则 (48) (49) 式(49)可改写为 (50) 对式(50)积分可得: (51) 基于以上的控制器设计和系统稳定性分析,给出如下定理: 定理1对于回转角速度不可测的智能船舶自动舵系统(3),基于状态观测器(10)、自适应模糊输出反馈控制器(43)和参数自适应律(44),通过适当地选取设计参数,闭环系统内所有信号是有界的,追踪误差和观测器误差收敛到零的一个小邻域内. 本文利用MATLAB进行计算机仿真,验证控制算法的有效性.仿真中用到的船舶参数:船长为126.0 m,船宽为20.8 m,满载吃水为8.0 m,方形系数为0.681,船速为7.72 m/s.通过计算得船舶运动数学模型参数[10]为a1=1,a2=30,K=0.478,T=216. 为跟踪信号选取能够代表实际性能要求的数学模型: (52) 其中,φm代表在船舶航向控制过程中φ(t)的期望性能,φr是命令输入信号. 仿真中考虑舵机影响,u(v)被描述为 (53) 其中,uM=40π/180. 在仿真中,模糊规则选取为 图1 模糊隶属函数Fig.1 Fuzzy membership functions 图2 本文航向系统状态曲线Fig.2 State curves of the proposed ship autopilot system 图2为智能船舶自动舵系统的自适应模糊输出反馈算法仿真结果.由图2可见:本文在考虑舵角输入受限和回转角速度未知的前提下,期望航向跟踪误差在指定范围内,兼顾了船舶航向实际性能需求;在跟踪过程中,误差趋于以零为中心的一个小邻域内,表明跟踪效果良好;控制舵角的历时曲线无较大超调量并趋于稳定,表明满足要求.仿真结果验证了本文所提算法的有效性. 1)与现有智能船舶自动舵系统的控制方法相比较,本文考虑了回转角速度不可测、舵角幅值受限和带有指定性能等智能船舶实际工程应用中的复杂情况,使系统的控制器设计和稳定性分析更为复杂. 2)经研究得出,算法在实现输出反馈控制的同时,确保了闭环系统内所有信号是有界的,系统的跟踪误差收敛到以零为中心的较小邻域内,是解决智能船舶自动舵输出反馈控制设计的一个较好的方法. 3)本文没有考虑工程应用中自动舵会出现的情况,未来将考虑故障诊断和状态约束等复杂情况的船舶自动舵输出反馈有限时间容错控制问题.
1.4 模糊逻辑系统


2 基于状态观测器的模糊自适应控制器设计
2.1 状态观测器设计
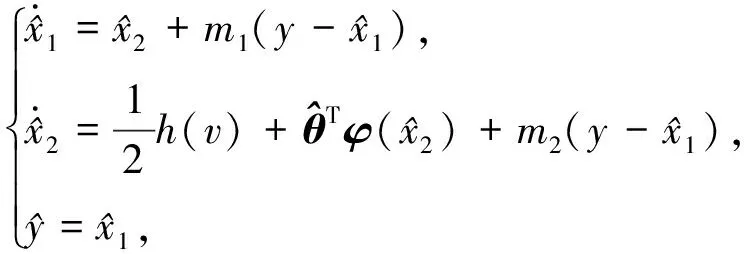


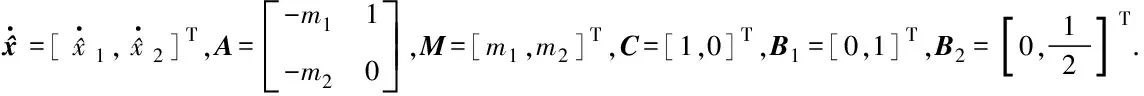
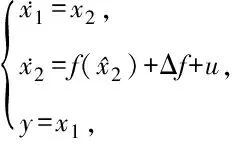

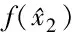
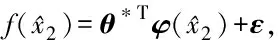
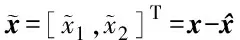


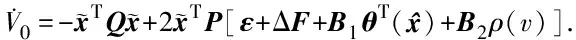


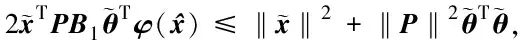

2.2 自适应控制器设计及稳定性分析

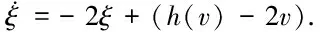





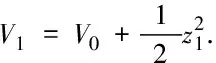

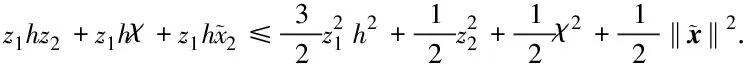
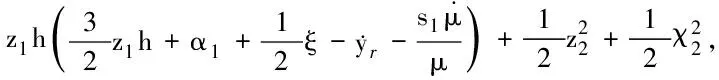

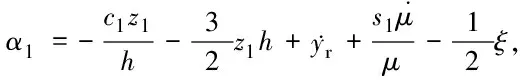
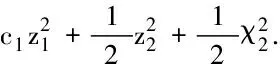


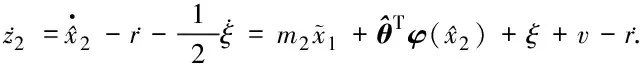
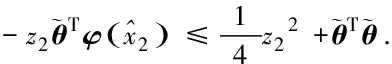
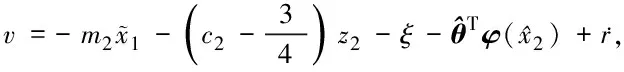




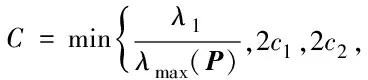
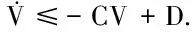

3 有效性实例仿真研究

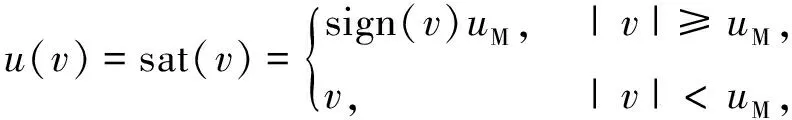
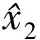
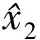
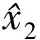
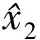
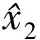
4 结论

