地铁隧道掘进爆破对既有埋地管道的动力影响*

梁 瑞，包 娟，周文海，王树江

(兰州理工大学 石油化工学院，兰州 730050)

为满足城市化规模扩大与基础设施建设，难免在埋地管线附近进行爆破施工作业[1,2]。爆破产生的瞬时高强度冲击波会对临近的地下管线造成严重的冲击，使管道承受较强激振作用而产生应力损伤，且在振动频率等于管道固有频率时，会引起共振位移破坏[3-6]。张黎明等利用现场爆破试验，结合应变强度准则拟合分析得到管道合成峰值振速与埋地管道轴向应变呈指数函数关系[7]；王栋等对埋地管道动力响应进行数值模拟研究，并通过现场试验验证了管道应变与地表变化具有比例关系[8]。Yilmaz T等通过改变爆破参数对托普恰姆水电站进行大量的振动分量监测研究[9]。郑爽英等利用有限元模拟和数值试验对影响埋地管道应力峰值的管道直径、壁厚、管道内压等5个爆破影响因素进行探究[10]；李镜培等利用LS-DYNA模拟和现场试验研究了炸药药量和管道壁厚对钢管破坏的影响情况[11]。郝郁清等结合屈服强度理论，建立了管道应变与对应单元振速的关系，并通过试验得到爆破振速及爆心距的函数关系及最小施工安全距离[12]。马华原等结合数值模拟和实地试验研究管土耦合模型的作用机理和应力应变规律，发现裂纹尖端的应力集中会导致管道开裂[13]。梁博等基于SPH-FEM法建立爆炸模型，分析了管体的扰动和土壤变形情况，得到管体迎爆面和背爆面的应变特征[14]。张震等通过现场监测和数值模拟，并结合最大拉应力强度理论确定了管道安全的地表爆破振速[15]。

目前，国内外研究学者对在不同的爆破载荷下埋地管道动力响应规律的研究，主要集中在管道整体的应力应变和振动速度，但就管道具体迎爆面、背爆面的应力应变、振速和管道能量的衰减研究较少。利用数值分析建立管土耦合的爆破荷载有限元模型，并通过管土体拉压本构关系分析其动力响应规律；在此基础上引入爆破振动波能量衰减公式，讨论埋地管道在爆破载荷下能量的波动衰减规律，提高了在爆破荷载作用下对埋地管道监测的可行性。

1 爆破载荷作用下埋地管道模型的建立

以南京4号地铁中段两站区间的南北两线隧道开挖掘进作为工程背景参考，隧道位于北京西路下方深10～18 m，站间总长约650 m，隧道呈马蹄形断面。岩体主要以沉积岩为主，在隧道南北两线上方1.1～9.7 m近区范围内，分布有较多的砖混建筑结构。地下1～2 m埋置有地下管线，考虑减小爆破振动对其影响，采用小距离掘进的松动爆破。

本文中模型包含的炸药、岩土体与管道均采用SOLID164类型单元，拟建立与实际工程相似的三维数值仿真模型。土壤层深4 m，下部岩层深16 m，岩土体整体尺寸为20 m×20 m×2 m；管道在土壤层中埋深2 m，岩土深度10 m处左右两侧各布置孔径φ70 mm，炮孔深1 m的圆柱孔炸药，单次起爆总药量Q为8.0 kg。两端同时起爆掘进作业，并对模型均采取实体网格进行划分。数值模型中管道为空管状态，炸药为连续耦合装药结构并设置药包中心位置起爆。在岩体外侧延无限伸区域及炸药边界面进行了位移约束与非反射边界条件，管道两端设置固定约束，模型结构如图1。管道与炸药、土体接触界面采取流固耦合算法，炸药采用ALE算法对单元进行流变控制，岩土体及管道均采用LAGRANGE算法控制进行求解，求解总时长设置为300 ms。炸药选取2#岩石乳化炸药，其材料类型为*MAT-HIGH-EXPLOSIVE-BURN，炸药状态方程选取不考虑炸药产物成分的JWL方程[16]。

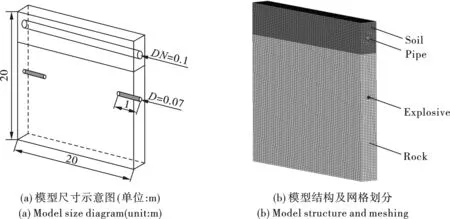
图 1 爆破掘进与浅埋管道结构模型(单位：m)Fig. 1 Blasting driving and shallow pipe structure model(unit：m)

(1)

式中：ρe为炸药密度；D为爆速；A、B、R1、R2均为材料参数；其中R1、R2为无量纲参数；ω为格林爱森常量；PCJ为爆轰压力；V0为比体积；e为初始比内能。见表1。

假定岩体为满足各向同性的弹塑性材料，选用*MAT-PLASTIC-KINEMATIC；土体选用材料类型为*MAT-SOIL-AND-FOAM。见表2。

表 1 炸药类型及状态方程参数Table 1 Types of explosives and parameters of equation of state

表 2 岩土体材料参数Table 2 Material parameters of rock and soil

表中：ρ为密度；E为弹性模量；G为剪切模量；μ为泊松比；σy为屈服极限；β为岩体硬化系数。

管道选用*MAT-PLASTIC-KINEMATIC作为低碳合金钢制管道的材料类型。见表3。

表中，ρ为密度；E为弹性模量；μ为泊松比；σy为屈服应力；Etan为剪切模量。

2 管道动力响应研究

2.1 模拟试验设计

见表4。

表 4 模型对照组Table 4 Model comparison group

2.2 管道受载应力分布分析

为了更好地分析爆破载荷下埋地管道的动力响应，管道的应力应变简化为理想线弹性与理想刚塑性两种不同状态下的本构关系。取管道上任意微小单元，其应力分量的大小和方向均已知如图2所示。

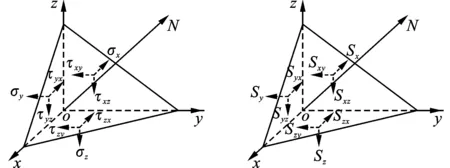
图 2 四面体微元受力图Fig. 2 Stress diagram of tetrahedron element

物体的剪切破坏主要由应力偏张量引起，定义Si为偏主应力，故偏应力主平面方程为

(2)

得到应力偏张量不变量

(3)

由上式可知，J2由三个方向的应力变化决定，考虑了中间主应力和平均应力，并且静水压力不仅对平均应力有影响，还会引起屈服破坏。由于管道的屈服破坏主要由偏应力第二不变量J2引起，而偏应力第二不变量主要反映剪应力的大小，故根据J2函数形式定义管道的应力破坏强度指标，即有效应力或广义剪应力σi为

(4)

(1)管道底部-迎爆面轴向应力分布规律

应力波于8～10 ms时作用于管道迎爆面两端并迅速沿管道壁面的轴向及环向传播，如图3有效应力云图可以看到轴向有效应力大于环向有效应力。考虑到管道的破坏主要由轴向和环向的应力波的动力响应造成，故下文对管道的轴向和环向动力响应进行研究。

图 3 管道有效应力云图Fig. 3 Cloud chart of effective stress of pipeline

管道底部作为迎爆面，为爆破冲击载荷最强的部位。沿轴线方向从管道底部左侧至右侧依次选取5个等距5 m的单元作为测点如图4(a)。提取各单元有效应力数据，绘制有效应力时程曲线。

对比3组不同管壁厚度的管组，分析受载管道轴向的应力波分布。如图5所示，(a)、(b)、(c)分别表示壁厚为4 mm、6 mm、9 mm管道的有效应力Effective Stress。

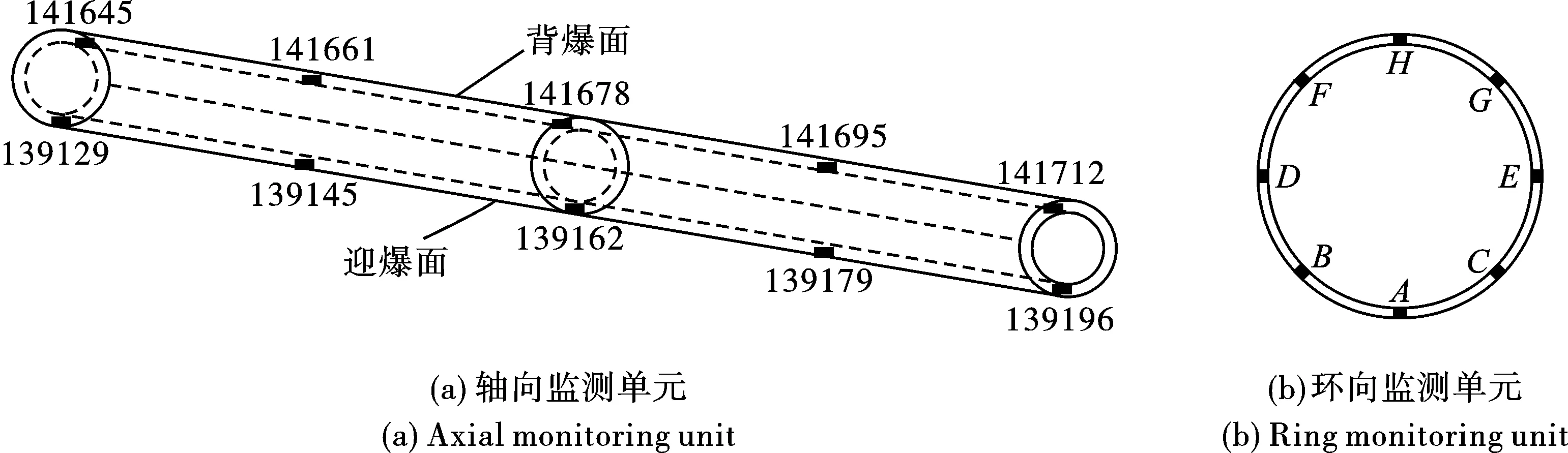
图 4 壁厚为4 mm的监测单元示意图Fig. 4 Schematic diagram of monitoring unit with 4 mm wall thickness

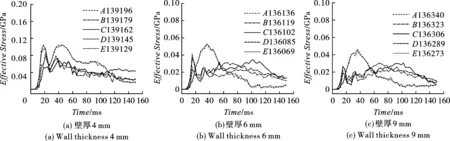
图 5 不同壁厚管道迎爆面轴向单元有效应力时程曲线Fig. 5 Time history curve of effective stress of axial element on the blasting face of pipeline with different wall thickness

分析迎爆面-管道底部有效应力时程曲线，发现随着管道壁厚的增大，有效应力峰值逐渐减小，说明管道壁厚在一定范围内，壁厚的增大可以有效增大管道的波阻抗，使管壁单元的有效应力减小，管道越不易发生破坏。由于B、D两单元距离爆源最近，在15～20 ms时的初始应力峰值均为最大值。

(2)管道顶部-背爆面轴向应力分布规律

同理提取背爆面监测单元，绘制不同壁厚管道组的有效应力时程曲线。如图6所示，(a)、(b)、(c)分别表示壁厚为4 mm、6 mm、9 mm管道背爆面轴向单元有效应力时程曲线。

分析背爆面-管道顶部有效应力时程曲线可以得到，随着管道壁厚的增大，有效应力峰值仍然逐渐减小，管道顶部作为背爆面，为管道最后受到爆破冲击载荷的部位。同时，对比迎爆面的管底单元有效应力峰值发现，背爆面受到应力波正向传播和地面反射波共同作用，产生应力局部放大效应。

2.3 管道受载速度分布分析

由于管道单元和岩体受冲击载荷发生非线性振动，且瞬时冲击载荷下应力变化过快，监测难度大，故选择分析更易监测的振动强度因子振动速度。

管道底部-顶部(迎爆面-背爆面)轴向速度分布规律。

同方法选取了沿管道轴线方向顶部单元，提取各单元振动速度数据，绘制振动速度时程曲线，分别表示不同管道壁厚迎爆面轴向的振动速度时程曲线，如图7、图8所示。

图 6 不同壁厚管道背爆面轴向单元有效应力时程曲线Fig. 6 Time history curve of effective stress of axial element on back blasting surface of pipeline with different wall thickness

图 7 不同壁厚管道轴向迎爆面单元速度时程曲线Fig. 7 Time history curve of unit velocity on the axial blast surface of pipeline with different wall thickness

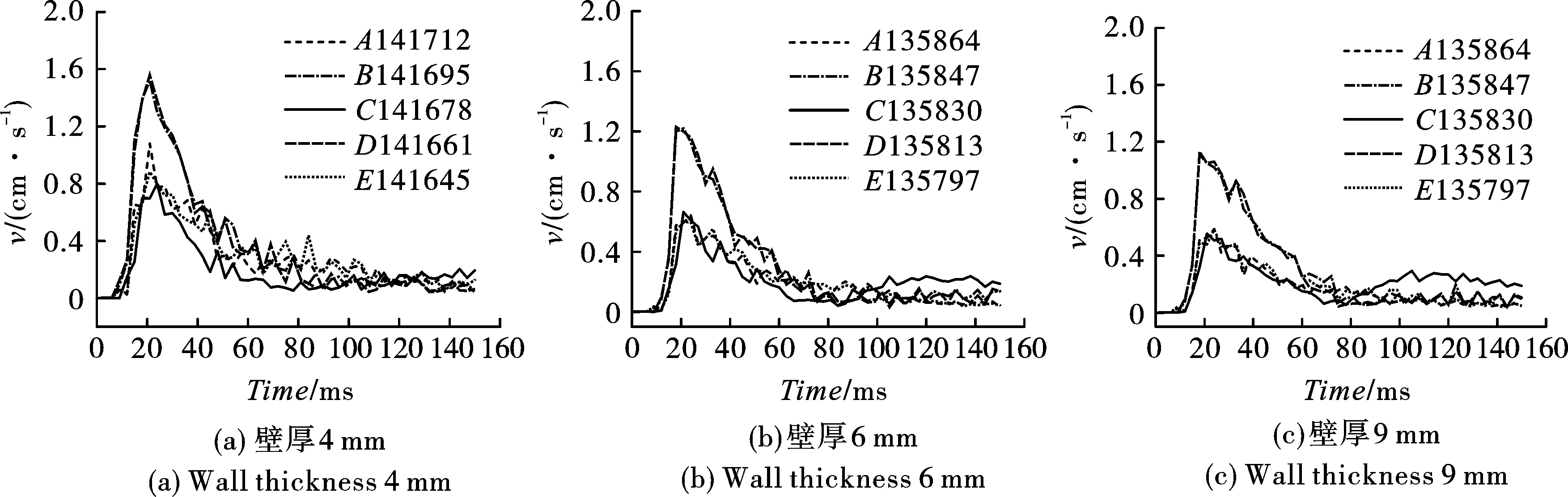
图 8 不同壁厚管道轴向背爆面单元速度时程曲线Fig. 8 Unit velocity time history curve of axial back blasting surface for different wall thickness pipeline

分析管道迎爆面-背爆面上监测单元的振动合成速度时程曲线，得到在10～21 ms时，振动速度迅速达到峰值，并逐渐发生衰减。管道两侧1/4处(B、D监测单元)由于与爆源的直线距离最短，其振动速度峰值为时程内最高值。随着管壁厚度的增大，峰值振速呈减小趋势；管道壁厚为4 mm的峰值速度的29%，而管道壁厚为6 mm的衰减速率为7%，管道壁厚越大，振动速率衰减速率越小。对比迎背爆面振速分布得到，不同壁厚管道振速由迎爆面至背爆面具有不同的衰减，但振速衰减相比应力衰减具有一定线性关系。

2.4 管道受载速度分布分析

为了直观对比探究管道在爆破振动波载荷作用下的应力分布、响应状态及传播规律，现分别绘制沿着管道轴向的迎爆面-背爆面，不同爆心距R下的有效应力峰值、振动合速度峰值的变化曲线图分析不同壁厚的管道轴向整体的受载振动响应如图9、图10所示。

(1)管道迎-背爆面有效应力峰值分布规律

分别以管道轴向长度作为x坐标，管道的迎爆面-背爆面单元的有效应力峰值为y坐标，分析三种不同壁厚的轴向迎-背爆面应力峰值变化规律如图9所示。

由图可知管壁厚度越大，有效应力峰值越小，衰减程度越小。管道两端受爆破载荷同时作用，应力波由两端向中间传播的过程中逐渐衰减，在管道中部应力峰值最小，薄壁管道应力峰值的衰减速率大于厚壁管道应力峰值的衰减速率。

图 9 轴向迎-背爆面应力峰值Fig. 9 Peak value of stress on the axial front back blasting surface

(2)管道迎-背爆面速度峰值分布规律

以管道轴向长度作为x坐标，管道的迎爆面-背爆面单元的振动合速度峰值为y坐标，分析三种不同壁厚的轴向迎-背爆面速度峰值变化规律如图10所示。

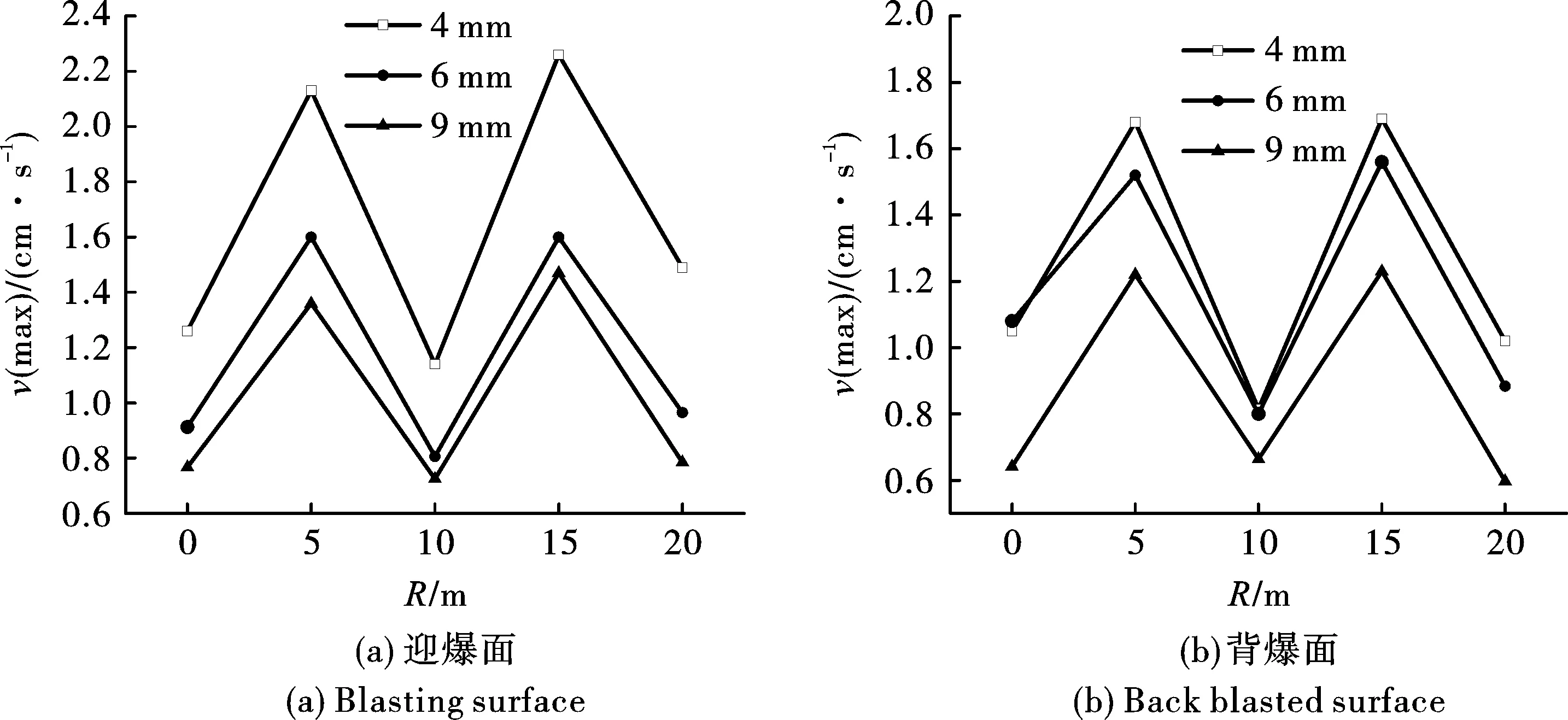
图 10 轴向迎-背爆面速度峰值Fig. 10 Peak value of axial velocity of front and back blasting surface

由图10可知迎爆面单元振动速度峰值较背爆面振动速度峰值更大，管道两侧1/4处振动速度最大，中间位置最小。结合图9的有效峰值应力分布，管道两端距离爆源最近，应力峰值最大，但速度峰值最大位置为管道两端的1/4处。说明振动速度的传播规律不是严格按照应力的线性传播进行衰减，更易受其他因素影响，如波的入射角，振动波以球面波传播至管道壁面上时，根据距离计算，速度峰值最大处与爆源的夹角为32°。

3 爆破振动波能通量计算

对管道的动力响应研究，除了对应力和振速的分析，更应考虑能量的改变，振动波能量传播规律对受载结构的响应分析能够综合考虑爆破振动强度、振动频率、持续时间的多因素共同作用。

爆破振动波传播是一个行进的点对点扰动过程，同时点的积分伴随着能量的传递。爆破振动强度的可量化因素通常以爆破振动强度因子进行运动描述，如质点振动位移、速度、加速度等。对于爆破强度A，其广义表达式为

A=KQαRβ

(5)

式中：A为爆破地震强度物理量；K为场地系数；Q为炸药量；α、β为衰减指数；R为测点至爆心距离。

对于某监测单元的爆破振动波能量的计算可以通过爆破振动波传播过程中经过该监测单元的能通量的积分求得。假设爆破振动波为无限连续介质中传播的球面波，在球面坐标系中应力张量的分量表示为

(6)

式中：u1为振动位移；r为爆心距；λ和μ为拉姆常数。由求和定则，能通量求解为

Φ=τijnjvj

(7)

而单元振动速度可由后处理中提取。设通过爆心距r处的能通量为定值，通过该单元截面的总能量P为

P=4πr2Φ

(8)

(9)

(10)

爆破振动波的能量随着波阵面继续扩展，围岩介质的开裂消耗了部分能量，所经过的质点振速逐渐降低，其微分表达式为

(11)

式中:Es为监测单元的爆破振动波能量；β表示振动波能量衰减量系数，负号表示能量的衰减。再对表达式积分得

Es=E0e-βr

(12)

式中:E0为爆源炸药能量转换为爆破振动波的初始能量；r为爆心距。又联合式E0=ηEe，η代表炸药能与转化成振动波初始能的百分比。得到爆破振动能量衰减公式

Es=ηEee-βr

(13)

对比式(5)，可以发现式(13)中爆破振动波能量Es对应强度物理量A；η对应场地系数K，而η与Ee的积表达为装药量Q的关系；式中的指数部分e-βr表达为能量的衰减形式，两公式间具有一致性。

通过爆破振动波衰减式(13)对表4中3组公称直径相同壁厚不同的管道环向监测单元分析，如图4(b)所示，沿管壁面底部至顶部依次选取8个单元并以字母A～H排序，监测单元具体数据的见表5。计算爆心距r并与式(10)计算得到的爆破振动波能量Es进行拟合回归。

首先将式(13)两边取对数

lnEs=lnη+lnEe+(-βr)

(14)

令y=lnEs，x=r，α=-β，b=lnη+lnEe，线性化表示为

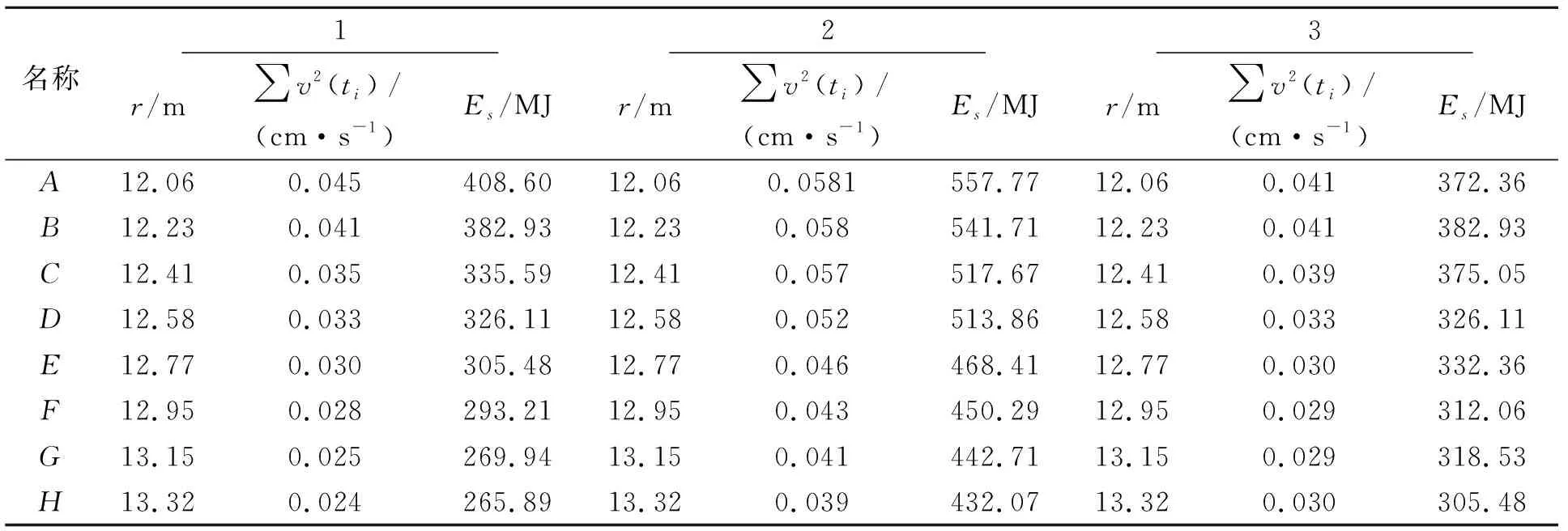
表 5 管壁单元峰值振速与振动波能量Table 5 Peak vibration velocity and vibration wave energy of tube wall element

y=ax+b

(15)

表中：r为爆心距；∑v2(ti)为单元时程速度平方和。

将表5数据代入式(15)进行线性回归拟合，得到管道中部环向监测单元的线性回归分析结果如图11。分析发现3组管道的振动波能量Es随爆心距r增大而减小；不同壁厚的管道能量衰减程度不同：壁厚为4 mm、6 mm、9 mm的管道，爆破振动波能量衰减量分别为142.71 MJ、125.7 MJ、66.88 MJ，两者近似呈负相关关系。分析3组管道振动波能量的衰减变化，发现在同种爆破条件下，管道壁厚增大2 mm和3 mm的爆破振动波能量衰减速率分别减少约12%和47%，随着管壁厚度增大，振动波能量在管道上的衰减幅度也下降。

尝试探寻管道监测单元振动波能量和对应振速的关系，将振动波能量与单元峰值速度进行拟合，得到爆破振动波能量Es与振动速度的平方v2近似正相关，且相关性均大于0.85，如图12。

图 11 能量与爆心距线性回归结果Fig. 11 Results of linear regression of energy and blast center distance

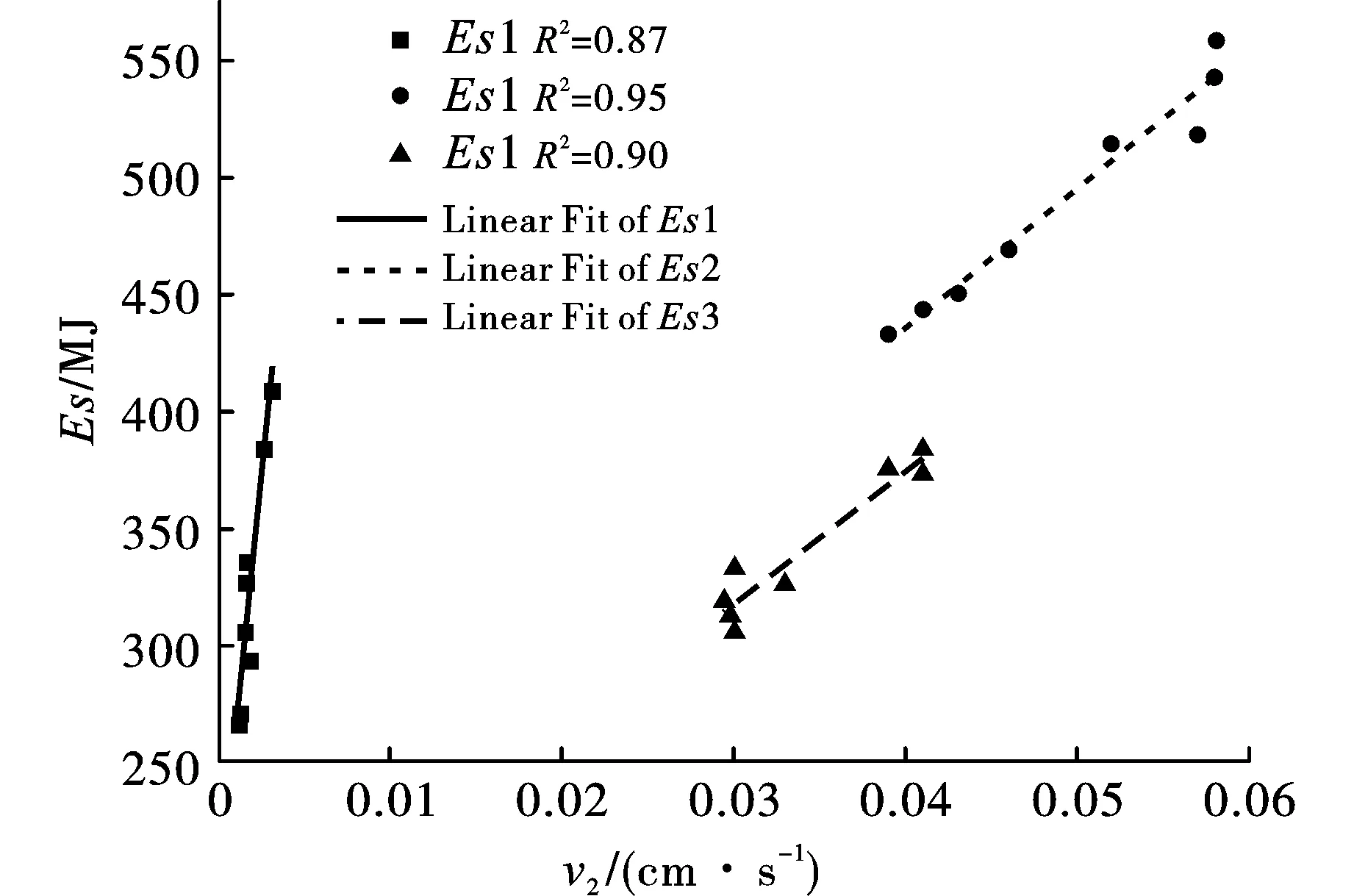
图 12 能量与速度平方线性回归结果Fig. 12 Energy and velocity squared linear regression results

为比较由衰减公式(13)拟合得到的衰减系数β与数值模拟结果计算得到的衰减率贴近程度，定义迎-背爆面振动波能量衰减率κ

κ=(EsA-EsH)/EsA

(16)

式中:EsA、EsH分别为管道迎爆面单元和背爆面单元的瞬时振动波能量。对管道迎爆面与背爆面振动波能量数据计算得到κ作为能量衰减率，通过能量衰减公式对三组不同壁厚的管道单元拟合回归得到η、β值，令i=T/D作为管道厚径比参数，如表6，κ值由表5计算得到。

表 6 管道回归结果与能量衰减公式Table 6 Pipeline regression results and energy attenuation formula

根据表6，绘制η、κ、β和厚径比的变化关系图如图13。

图 13 i与η、κ、β变化关系Fig. 13 Relationship between i and changes of η,κ,β

分析得管道厚径比i<0.0525的管道，炸药能的衰减更为显著；厚径比0.0525≤i≤0.05375，管道能量衰减系数β、炸药能转换率η与迎-背爆面能量衰减率κ的能量衰减程度均处于26.7%；厚径比i≥0.05375，管道振动波能量的衰减更加明显；管道厚径比i≥0.06时，管道环向的振动波能量衰减规律基本相似。随着管道厚径比i增大，管道环向监测单元的η、κ与β均逐渐减小，管道壁面的振动波阻抗增大且管道对振动的响应敏感度降低，振动波能量衰减程度变弱。爆破振动波能量衰减模型关于爆心距回归得到的衰减率β，其数值及变化趋势与测点数据计算得到的κ贴近程度较高，表明在爆破振动波对管道的动力响应分析中建立的能量衰减模型较为准确。

4 结论

通过模拟在爆破载荷作用下，不同壁厚埋地管道的动力响应，对其有效应力、振动速度和能量变化规律进行分析：

(1)通过分析迎爆面-背爆面轴向监测单元应力时程曲线和速度时程曲线，发现管道迎爆面1/4(B、D单元)处存在应力集中现象，在20～50 ms时管道有效应力达到峰值；管道背爆面有局部应力放大效应；在10～21 ms时管道迎爆面和背爆面的振动速度达到峰值。

(2)随着管道壁厚的增加，管道迎爆面和背爆面同一位置处的轴向有效应力和速度均逐渐减小。在管道两端，迎爆面和背爆面的有效应力峰值最大；距管道两端1/4处，迎爆面和背爆面的振动速度峰值最大。

(3)建立管道振动波能量衰减模型，拟合得到管道环向振动波能量衰减量与管道壁厚呈近似负相关关系，管壁振速的平方与振动波能量呈一次函数关系；当管道厚径比i<0.0525时，炸药能的衰减最快，0.0525≤i≤0.05375时，衰减指标η、β、κ数值均为26.7%，且i≥0.06时管道环向监测单元各项衰减指标规律趋于一致。

(4)在本文工况下，模拟所得的管道振速峰值分布于1.0～2.25 cm/s范围内，将《爆破安全规程》中爆破振动波的振动速度与振动频率作为安全判据，管道处于安全状态。