基于MATLAB的4YF-1300型大方捆打捆机喂入机构运动仿真分析与优化*
王海超,孙小添,刘瑜,裴志永,郭根胜
(1. 内蒙古农业大学能源与交通工程学院,呼和浩特市,010018; 2. 内蒙古农业大学机电工程学院,呼和浩特市,010018)
0 引言
近年来,我国饲草收获主要采用成捆收获方式,打捆机械可一次完成饲草捡拾、压缩成型和绑捆等工作,极大地节约了劳动成本,提高了生产率,改善了牧民生活水平。据不完全统计,经饲草打捆机械收获的饲草平均密度增大10倍左右,运输和储存成本下降70%左右[1-2]。国内许多畜牧机械生产企业纷纷开展打捆机械的研发与生产,以满足市场需求。
大方捆打捆机由于结构和性能特点,相较于小型打捆机生产效率、打捆成型密度和质量更高。自20世纪70年代中期开始生产大方捆打捆机,随着技术水平的不断提高,逐渐形成产业化[3]。目前市面上使用的大方捆打捆机主要为进口产品,最具有代表性的有德国生产的QUADRANT大方捆打捆机、法国生产的LSB系列大方捆打捆机和美国生产的BIGBALER系列大方捆打捆机[4-6]。中国大型打捆机相对较少,目前只有中国农业机械化科学研究院在借鉴进口打捆机械研究的基础上,设计研发了9YDF系列打捆机。
大方捆打捆机工作过程相对复杂,捡拾喂入机构性能是影响后续饲草压缩成型质量关键,直接影响作业效率。本文在已有研究基础上,采用SolidWorks软件建立喂入机构三维模型,进而构建大方捆打捆机喂入机构的运动方程;采用MATLAB进行编程求解,得到喂入机构的运动轨迹图,旨在为后续系统的优化设计提供基础,为大方捆打捆机喂入机构设计提供借鉴[7-10]。
1 4YF-1300型大方捆打捆机喂入机构填料过程分析
底端喂入方式是打捆机喂料主要方式,底喂入式大方捆打捆机主要由螺旋输送器、喂入机构、预压室、档草爪、链轮、电控装置等组成,其中喂入机构主要由小喂入叉和大喂入叉组成[11]。具体工作过程可分为4步。
1) 作业时,饲草经捡拾器拾起,拾起饲草经螺旋输送器输送至喂入机构,喂入机构中的小喂入叉位于预压室进料口上方,随着小喂入叉的运动,将饲草不断的沿预压室内壁推至挡草爪的下方,如图1(a) 所示。
2) 预压室在未填满饲草前,驱动链轮将一直保持空转,此时固定在驱动链轮轴上的大喂入叉保持初始位置不动,饲草在挡草爪的阻挡下被预压缩,如图1(b) 所示。
3) 当饲草在预压室内达到一定密度时,将触发电控装置,电控装置驱动电机打开挡草爪,饲草上行。由于大喂入叉与活塞运行同步,经预先调试,当活塞处于空行死点时,大喂入叉将滞留在预压室内的饲草一次性地喂入到压捆室内,如图1(c)和图1(d)所示。
4) 当活塞开始压缩时,喂入机构和挡草爪返回到原起始位置,为下一工作循环做好准备,从而实现填料过程。

(a)

(b)

(c)

(d)
2 喂入机构三维建模
根据实际参数,采用SolidWorks对小喂入叉和大喂入叉构建三维模型,如图2、图3所示。通过对模型进行分析,适当优化结构参数,消除零件间干涉。

图2 小喂入叉三维装配图Fig. 2 3D assembly drawing of small feeding fork

图3 大喂入叉三维装配图Fig. 3 3D assembly drawing of large feeding fork
3 喂入机构位置方程确定
3.1 小喂入叉位置方程
根据小喂入叉结构特点,小喂入叉机构运动简图如图4所示,D为坐标原点,各杆矢量围成封闭多边形ABCDA。其矢量方程为
(1)
式中:l1——曲柄DC长度,mm;
l2——连杆CB长度,mm;
l3——摇杆AB长度,mm;
l4——机架AD长度,mm。

图4 小喂入叉机构运动简图Fig. 4 Movement diagram of the small feeding fork mechanism
各杆件在x方向和y方向应满足
(2)
式中:φ1——曲柄DC转角,(°);
φ2——连杆CB转角,(°);
φ3——摇杆AB转角,(°)。
为保证喂入叉与其他机构运动无干涉,小喂入叉机构运动应满足
(3)
式中:L——小喂入叉曲柄回转中心距压缩室最近边缘的水平距离,mm;
H——小喂入叉曲柄回转中心距压缩室最近边缘的垂直距离,mm;
le——小喂入叉CM长度,mm;
θ1——小喂入叉CM转角,(°)。
综上,由式(2)、式(3)可知,当曲柄做回转运动时,小喂入叉端点M会随曲柄做一定规律回转运动,M点坐标值与曲柄DC转角φ1、长度l1以及小喂入叉CM转角θ1、长度le相关,由此可推导出M点的位置方程
(4)
将式(4)对时间t求导,则可得出M点速度方程
(5)
式中:vM x——小喂入叉端点M在x轴方向线速度,mm/s;
vM y——小喂入叉端点M在y轴方向线速度,mm/s;
w1——曲柄l1绕A点旋转角速度,(°)/s;
w11——小喂入叉le绕C点旋转角速度,(°)/s。
3.2 大喂入叉位置方程
大喂入叉机构运动简图如图5所示。
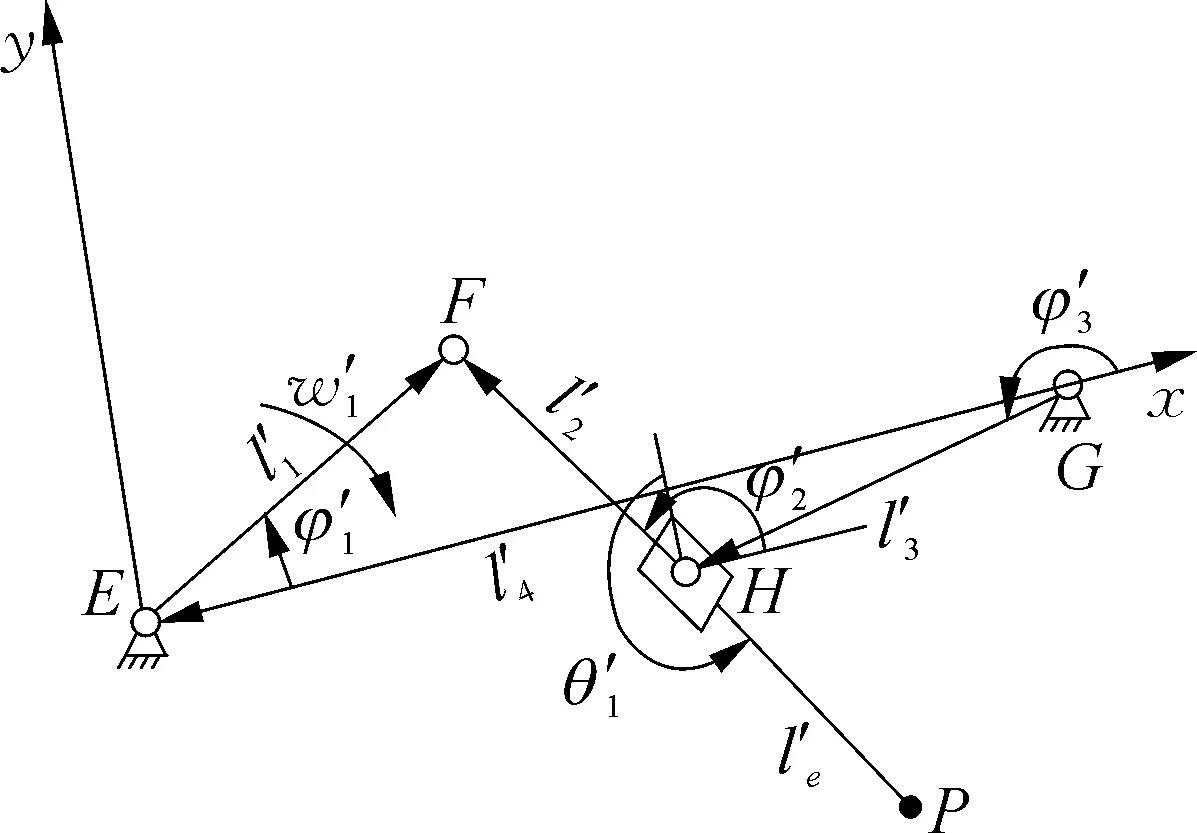
图5 大喂入叉机构运动简图Fig. 5 Movement diagram of the large feeding fork mechanism
经分析,大喂入叉机构位置方程应满足
(6)
式中:l′1——曲柄EF长度,mm;
l′2——导杆FH长度,mm;
l′3——摇杆HG长度,mm;
l′4——机架EG长度,mm;
φ′1——曲柄EF转角,(°);
φ′2——导杆FH转角,(°);
φ′3——摇杆HG转角,(°);
L′——大喂入叉曲柄回转中心距压缩室最近边缘的水平距离,mm;
H′——大喂入叉曲柄回转中心距压缩室最近边缘的垂直距离,mm;
l′e——大喂入叉HP长度,mm;
θ′1——大喂入叉FP转角,(°)。
由式(6)可知,当曲柄做回转运动时,大喂入叉端点P会随曲柄做一定规律回转运动,P点坐标值与曲柄EF转角φ′1、长度l′1以及大喂入叉FP转角θ′1、长度l′e相关,由此推导出大喂入叉端点P位置方程
(7)
将式(7)对时间t求导,则可得出P点速度方程
(8)
式中:vPx——大喂入叉端点P在x轴方向线速度,mm/s;
vPy——大喂入叉端点P在y轴方向线速度,mm/s;
w′1——摇杆l′1绕E点旋转角速度,(°)/s;
w′11——大喂入叉l′e绕H点旋转角速度,(°)/s。
4 试验设计及结果分析
4.1 试验设计
喂入机构各指标实际尺寸为:l1=160 mm,l2=418 mm,l3=435 mm,l4=495 mm,le=270 mm;l′1=382 mm,l′2=175 mm,l′3=226 mm,l′4=355 mm,l′e=520 mm,θ1=θ′1=60°。当l1、l′1、θ1和θ′1为定值时,M点和P点坐标值随曲柄转角φ1、φ′1变化而变化,故曲柄转角φ1和φ′1取k个特定值,运用MATLAB仿真,则可生成M点和P点的运动轨迹曲线。曲柄l1绕A点旋转角速度w1=514°/s,运动周期T1=0.7 s,摇杆l′1绕E点旋转角速度w′1=240°/s,运动周期为T′1=1.5 s。由此确定小喂入叉仿真模拟时长为0.7 s,大喂入叉仿真模拟时长为1.5 s,时间间隔为0.1 s,每秒帧数为500,精确度为0.000 1。
大喂入叉采用的是曲柄滑块机构,仿真求解较复杂,为简化,将滑块简化为铰接。采用MATLAB工具箱fsolve函数进行求解。程序编写时需要特别注意:(1) 设置数组,用于曲柄旋转时各特定点角度的存储;(2) 将角度值均分为41个点,9°为一个间隔,同时取两个端点值,使图像光滑封闭。
4.2 结果分析
大、小喂入叉的端点运动轨迹如图6、图7所示。小喂入叉和大喂入叉的轨迹均为腰果型,且坐标值也有相对高的精度。相较于小喂入叉,大喂入叉在x轴和y轴方向行程更大,这更有利于将饲草充分喂入压缩室,保证压缩效率。点A和点①为大、小喂入叉起始点,点C和点③为大、小喂入叉运动最高点,点①→点③及点A→点C为小喂入叉和大喂入叉工作行程,点③→点①及点C→点A为小喂入叉和大喂入叉返回行程。
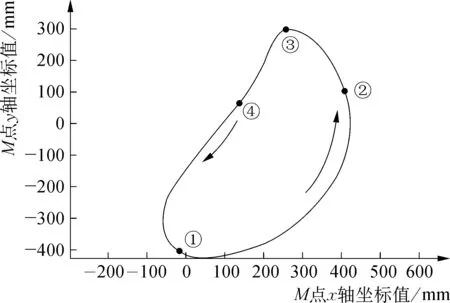
图6 小喂入叉端点M轨迹图Fig. 6 Trajectory diagram of the end point M of the small feeding fork

图7 大喂入叉端点P轨迹图Fig. 7 Trajectory diagram of the end point P of the large feeding fork
大、小喂入叉的端点P和M速度变化曲线如图8、图9所示。
点A和点①为大、小喂入叉工作起始点,结合图6、图7轨迹图对大、小喂入叉端点速度变化曲线分析结果如下。
1) 小喂入叉端点M由点①至点③为工作行程阶段,所用时间为0.35 s,期间水平速度vM x、竖直速度vM y及合加速度vM均先增大后减小,并伴有方向改变,当时间为0.19 s时,端点M运动至点②,速度达到最大值,合速度为5 985.03 mm/s;大喂入叉端点P由点A至点C为工作行程阶段,所用时间为0.75 s,期间水平速度vP x、竖直速度vP y及合加速度vP均先增大后减小,方向不断改变,在0.25 s时,vP y达到最大值,0.60 s时,vP x达到极值,在0.375 s时,端点P运动至点B,vP为6 124.38 m/s,达到最大值。

图8 小喂入叉端点M速度变化曲线图Fig. 8 Speed change curve of the end point M of the small feeding fork

图9 大喂入叉端点P速度变化曲线图Fig. 9 Speed change curve of the end point P of the large feeding fork
2) 小喂入叉端点M由点③至点①合速度先增大后减小,在0.45 s时,运动至点④,合加速度为6 285.47 m/s,即此时小喂入叉完成喂料后,快速离开预压室,向起始位置回退;大喂入叉端点P由点C至点A过程中,合速度先增大后减小,在0.88 s时,运动至D点,合加速度为5 001.36 m/s,大喂入叉实现快速回退,速度逐渐减小,而后逐渐趋于平稳,避免了喂入叉过度打击饲草花叶,有利于饲草喂入。
3) 大喂入叉和小喂入叉在点A和点①处速度最小,实现了饲草的平稳充分喂入。
5 参数优化及验证
5.1 参数优化
经前期试验,按大、小喂入叉原有尺寸进行作业时,小喂入叉完成2次喂料,大喂入叉完成1次喂料,二者配合完成压捆。经分析,适当提高大喂入叉在压缩室停留时间,可提高预压室和压缩室内充草量,进而提高大方捆打捆机工作效率。已知压缩活塞途经喂料口回退至推进过程所用时间为0.362 s,在满足大喂入叉尺寸不超过压缩室水平和垂直距离,且不发生干涉前提下,增加大喂入叉l′e长度,进行试验。l′e原长为520 mm,以20 mm为步长,l′e不超过590 mm为上限,通过仿真计算出大喂入叉停留于压缩室内的时间,轨迹仿真结果如图10所示,大喂入叉在压缩室内停留时间如表1所示。

图10 改变l′e长度P点运动轨迹Fig. 10 Trajectory of point P of changing the length of l′e

表1 改变l′e长度P点在压缩室内停留时间Tab. 1 Residence time of point P in the compression type after changing the length of l′e
由图10知,当改变曲柄l′e长度时,P点轨迹形状不会发生变化,但P点在x轴和y轴方向的坐标值会随着l′e长度的增大而增大,从而提高了大喂入叉端点P在压缩室内的停留时间。由表1知,当l′e=580 mm时,大喂入叉端点P在压缩室内停留时间为0.358 s,与压缩活塞从回退避开压缩室喂料口到推进经过喂料口时间相差0.004 s,时间间隔过短,极易发生故障,考虑实际因素,选择l′e=560 mm,时间间隔为0.020 s,基本满足实际需求。
5.2 试验验证
根据仿真结果,加工生产l′e=560 mm大喂入叉,与原尺寸喂入叉喂入量进行对比。经试验,当l′e=520 mm时,整周期喂入秸秆量为1.536 kg;当l′e=560 mm时,整周期内喂入秸秆量为1.744 kg,喂入效率提高13.54%,可较好地应用于农业生产。
6 结论
1) 通过运动分析,建立了大、小喂入叉的轨迹和运动方程。通过MATLAB仿真求解,得到两喂入叉端点轨迹和速度变化曲线,并最终实现了参数优化。两喂入叉端点运动轨迹呈腰果型,小喂入叉运动周期T1=0.7 s,大喂入叉运动周期T′1=1.5 s。
2) 大、小喂入叉无论工作行程还是回退行程,其端点合加速度均呈先增大后减小趋势,工作行程中,小喂入叉端点M运动至点②时速度达到最大值,合速度为5 985.03 mm/s,大喂入叉端点P运动至B点时速度达到最大值,合速度为6 124.38 m/s;返回行程中,小喂入叉端点M运动至点④时速度达到最大值,合速度为6 285.47 m/s,大喂入叉运动至D点时速度达到最大值,合速度为5 001.36 m/s。
3) 适当提高大喂入叉在压缩室停留时间,可提高预压室和压缩室内充草量,进而提高大方捆打捆机工作效率。当l′e=560 mm时,整周期内喂入秸秆量为1.744 kg,喂入效率提高13.54%,该仿真初步验证了理论分析的准确性,可较好地应用于农业生产。

