基于博弈论的SDN多控制器负载均衡机制研究

刘晓凤，王灵矫**，郭 华

(1. 湘潭大学 信息工程学院，湖南 湘潭 411105；2. 湘潭大学 智能计算与信息处理教育部重点实验室，湖南 湘潭 411105)

软件定义网络（Software Defined Network，SDN）体系结构的主要特点在于控制平面与数据平面的解耦，具有可编程、自动化和网络控制等特性，操作者可灵活构建可编程网络以适应不断变化的网络环境. 网络规模的扩展使得单控制器的部署已不能满足现有网络需求. 因此，一些研究人员相继提出了一系列逻辑上集中，物理上分布的多控制器体系结构（HyperFlow、Onix、Kandoo）[1-3]. 在物理上集中的控制平面由整个网络的单个控制器组成，这是理论上理想的设计选择. 但是，随着SDN中交换机数量的增加，集中控制器在处理越来越多的请求并同时努力实现相同的性能保证时，它可能变得不堪重负. 而且，由于单点故障，SDN控制器的故障会导致整个网络瘫痪. 因此，有人提出使用多个物理分布式SDN多控制器以提高系统的可扩展性和可靠性.

现有的分布式SDN多控制器体系结构存在的问题之一是SDN交换机与控制器之间的静态映射，使得控制平面无法适应流量变化. 当网络中的流量发生巨大的变化时，如果SDN转换控制器映射是静态的，那么巨大的变化可能会导致控制器之间负载的不均衡，即有些超负荷，有些未充分利用. 过载的控制器将以增加的延迟响应切换请求，从而恶化用户的体验.

目前现有的通过交换机确保负载均衡的方案，大多虽然能够动态地调整网络的负载，但是在交换机迁移过程中，对目标控制器进行选取时，仅考虑时延或控制器容量，易导致目标控制器选取僵化.简单的主从控制器按距离分配进行交换机迁移时，当最近邻控制器负载较重时，易导致迁移震荡问题.

针对多控制器负载不均衡问题，本文给出了一种基于博弈论的负载均衡机制（Game Theory Load Balancing，GTLB）. 其主要创新工作如下：

（1）结合交换机迁移思想，利用交换机迁移概率、交换机与控制器的传输时延和换机迁移成本实现GTLB机制的建模.

（2）构建博弈域模型，实现了以迁移概率确定迁移交换机、粒子群算法选择目标控制器和迁移计时模型，提高交换机迁移效率.

（3）进行仿真实验，验证GTLB机制性能.

1 相关工作

传统的SDN实现依赖于一个集中式控制器，在性能和可伸缩性方面有一些限制. 一些研究工作表明，分布式控制器的部署是解决问题的一种有效的方法[4-6]. 为了在分布式网络中获得更好的性能和可伸缩性，Bari等[7]提出一个框架，该框架可以调整控制器的数量并委托每个控制器，可以最低限度降低通信开销的同时最大程度减少流建立时间. 但是，这很容易导致网络不稳定. 为了实现一个可扩展的SDN控制平面，Cheng等[8]提供了一个博弈决策机制，将交换机迁移问题表示为一个具有多个资源维度约束的集中式可用资源最大化问题. 对多控制器负载均衡的研究过程中，Heller等[9]以交换机和控制器之间的时延为迁移度量，研究了控制器不同部署位置对交换机迁移的影响，取得了一定的理论成果. Dixit等[10]提出弹性分布式控制器体系结构“ElastiCon”，以网络状态为据增加或减少控制器池的剩余控制器，迁移控制器之间的负载. 史久根等[11]提出了多控制器优化方案，重点关注控制器负载均衡和控制器之间的时延，权衡多个相互矛盾实现优化目标. Adlen等[12]提出使用博弈论优化部署SDN控制器，以时延、通信开销、控制器负载均衡获取均衡度量，实现控制器部署数量和位置的优化. Fan等[13]提出基于博弈论的单一控制器主控制器重选机制.

2 分析与建模

2.1 问题描述多域SDN网络结构如图1所示，4个控制器分别与交换机连接构成子域. 每个交换机可以配备3种控制器：主控制器、从控制器、等价控制器[14]. 若子域2聚集了大量的流请求，c2就会过载，它所控制的交换机通过选择从控制器作为交换机新的主控制器来实现交换机迁移. 多域SDN网络的交换机迁移需要完成两项工作：①确定迁移交换机和目标控制器；②设计有效的交换机迁移模式，提高负载均衡效率.

2.2 SDN博弈模型组成

2.2.1 SDN博弈域 博弈域（Game Domain，GD）是一个临时的、松散的且具有特定目标的联盟，SDN中的GD是为交换机迁移选定的区域且仅与过载控制器和相关相邻控制器有关[15]. 在图1所示的4个子域中，c2是过载控制器，G4负载较高，则G2的GD可为F2={G1,G2,G3}.

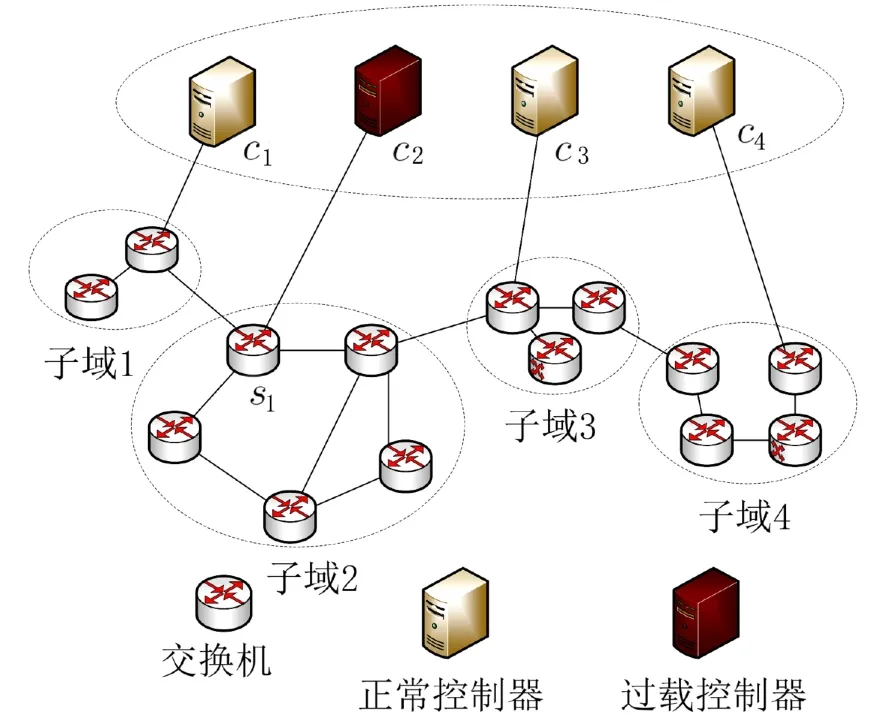
图1 分布式多控制器部署的体系架构Fig. 1 An architecture for distributed multi-controller deployment

GTLB机制的基本思想是构建博弈域和实现交换机无缝迁移. 过载控制器cr（r∈（1,M））和相邻的子域构建GD，并将过载控制器控制子域下的交换机si（i∈（1,N））迁移至目标控制器ck(k∈（1,M））.

2.2.2 SDN博弈模型 根据图论相关知识，整个网络可用无向图G=(V,E) 表示，其中V是网络的所有节点集合，E是所有链路的集合. 假设一个网络由M个控制器和N个交换机组成，控制器集合C={c1,c2,···,cM}，交换机集合S={s1,s2,···,sN}，所以节点总数|V|=M+N. 假设所有控制器的位置都已优化好[16]. 设备i和j之间的跳转定义为dij，xij表示交换机si和控制器cj的连接关系为

图1中，GTLB博弈模型定义为 θGTLB={C,L,U}，其中C是博弈的参与者集合，过载控制器c2作为博弈者向邻近控制器发送构建博弈域请求，博弈的参与者集合为C={c1,c2,c3}；L是每个参与者可选择的行动方案集合，若控制器c2选择交换机si为迁移对象，每个参与者cr具有两种策略，即Lr={cr接受交换机si,cr拒绝交换机si}；U是所有参与者在某一组特定策略组合下的效用，其效用函数包含传输时延和迁移成本两部分[17-18].

定义1交换机si与控制器cj之间的传输时延为二者之间的最小距离，则所有交换机与控制器之间的传输时延Vij如式（2）所示：

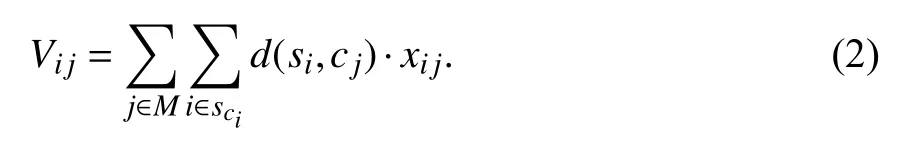
定义2交换机迁移成本Pm包括迁移规则安装成本Pru、通信成本Pc和迁移请求成本Pre.

确定需要迁移的交换机si后，控制器cr必须在域内将flow_mod规则安装到迁移交换机. 则Pru如下：

其中，δ表示flow_mod包的平均大小.

迁移交换机si和目标控制器ck进行正常的信息传递时产生交换机通信成本为

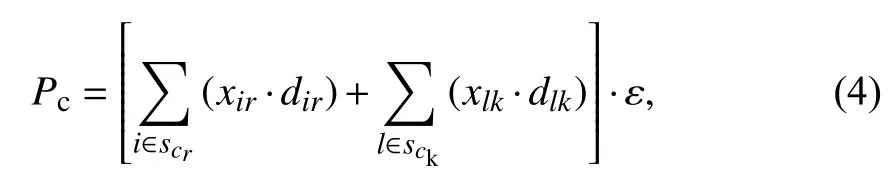
其中，ε表示交换机的平均通信速度，xir和xlk分别表示cr和ck域内交换机与控制器的连接关系.

当迁移交换机向目标控制器发送流请求时，生成Pre，表示为

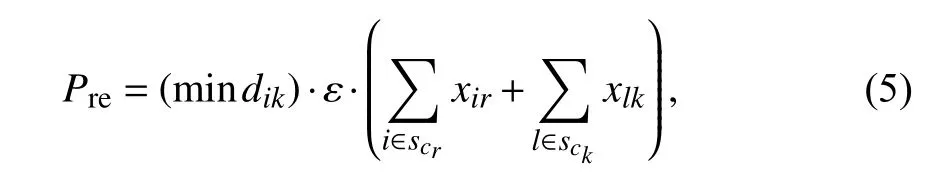
其中，mindik表示迁移交换机到目标控制器的最小跳数.

因此，交换机迁移成本Pm是上述3种成本的总和，表示为

综合考虑控制器与交换机之间的传输时延和交换机迁移成本，将博弈域中的目标控制器的选择问题转化为多代价线性规划问题进行求解，因此，效用函数

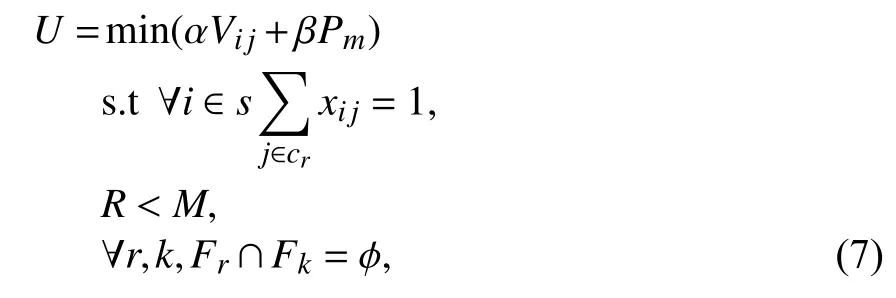
其中，α、β表示权值，Fr和Fk表示任意两个不同的博弈域，R表示Fr内的控制器数量. 约束条件分别表示子域中每一个交换机只有一个主控制器. GD中的控制器数量少于网络控制器的总数. 任意两个GD之间没有交集，并且控制器只属于一个GD.

3 GTLB的设计与实现

基于GTLB的基本原理及建模思想，GTLB的流程图如图2所示，主要分为3个阶段：①分析网络负载信息，判定控制器的负载情况；②利用博弈论和粒子群算法选择迁移交换机和目标控制器[19]；③设置倒计时实现交换机无缝迁移和控制器角色转换[20]；最后判断控制器负载均衡状况. 如果判定结果符合控制器资源利用率的约束条件，跳出GTLB，否则返回第一阶段继续.

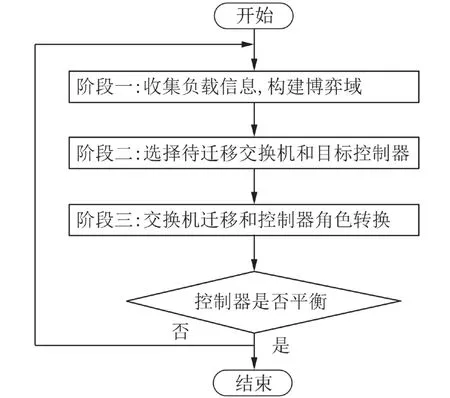
图2 基于博弈论的负载均衡机制的流程图Fig. 2 Flow chart of load balancing mechanism based on Game Theory

3.1 收集网络负载信息，构建博弈域网络负载信息包括链路信息，跳转信息和控制器资源利用率γr，控制器资源利用率如式（8）所示，表示控制器的处理容量被其管理下的交换机占用的程度. 并根据所有控制器的资源利用率求得这些控制器平均资源利用率.

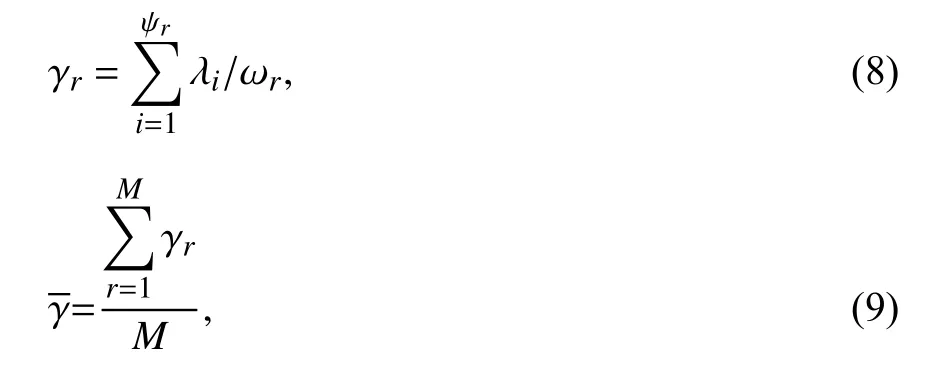
其中，λi表示交换机si的流量请求速率（主要包括Packet-in消息），Ψr表示cr控制的交换机数目，ωr表示控制器的处理容量.

博弈域的构造采用遍历搜索方法，流程如下：收集网络中的各类信息，设定控制器的过载条件，如式（10）所示，控制器的过载情况由控制器状态γr决定. 如果 0.9≤γr≤1，那么控制器cr是过载的，cr将向相邻的控制器cn发送请求，cn有两种选择意向，根据式（11）的相应条件选择适当的策略P，联合所有同意的邻居控制器构建博弈域.

3.2 迁移目标选择

3.2.1 迁移交换机si的选择 为了尽可能快地降低过载控制器的负载，优先选择迁移流请求率较高且距离过载控制器较远的交换机. 交换机的迁移概率定义为ρir，如式（12）所示：

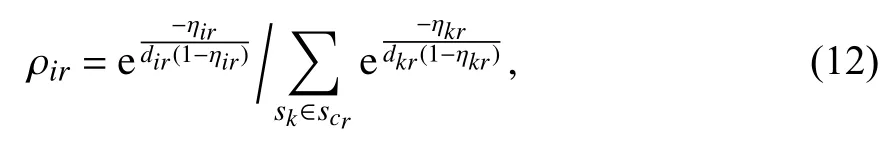
其中，ηir表示交换机si在控制器cr上所占用的控制资源，dir表示交换机与控制器之间的跳转. 迁移ρir值最大的交换机被迁移.

3.2.2 目标控制器ck的选择 利用粒子群算法在博弈域中选择最优目标控制器，算法步骤如下：

步骤 1初始化粒子的位置x0和速度v0;

步骤 2根据式（13）计算每个粒子的适应值，找出每个粒子的个体极值p、全局极值g，

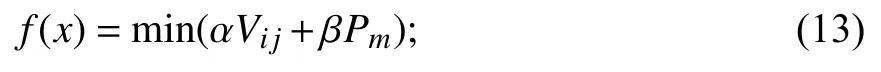
步骤 3根据公式（14）和（15）更新粒子的速度与位置

步骤 4计算更新位置粒子的适应度；

步骤 5更新个体极值、全局极值；

步骤 6重复步骤2～5，直至达到规定迭代次数.

3.3 目标迁移实现GTLB的迁移过程如图3所示. 过载控制器cr选择迁移交换机si并向目标控制器ck发送迁移信号Move.ck接受到迁移信号后回复Move-start消息，选择一个随机数n开始倒计时(迁移交换机和相邻控制器数量越多，以及控制器资源利用率越高，倒计时设置越短)，其中n由式（19）生成，其中l是与控制器cr相连的交换机集合，Nr是相邻控制器cn的集合. 在n下降到0之前，如果交换机si迁移完成，si的主控制器转移到ck，cr成为的si从控制器，GPF自动解散，广播更新消息到整个网络. 倒计时超时或cr仍处于超载状态，重置倒计时和GTLB回到重建博弈域.

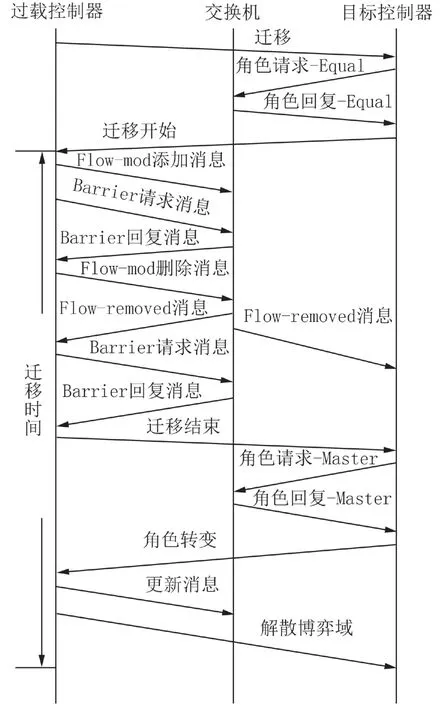
图3 交换机无缝迁移具体过程Fig. 3 Switch seamless migration process

4 仿真实验

4.1 仿真环境设置根据文献[21]建立仿真实验环境. 采用Ubuntu 16.04操作系统，Floodlight为实验控制器，Mininet部署网络拓扑. 实验拓扑取自OS3E，通过Iperf软件模拟交换机发包分组测试算法.

以文献[22]描述的流量特征配置实验参数，流的大小呈现分布式和具有不同的到达速率，流平均速率为500 K/s. 假设所有控制器具有相同性能，处理容量的上限为ωr=10 MB，资源利用率γr是在0和1之间，Flow_mod数据包δ=30 Byte，交换机间的通信速率ε=15 kb/s，α∶β=1∶1，学习因子c1=c2=2.

4.2 仿真分析实验比较GTLB与文献[4]中多控制器备份机制（Multi Controller Backup，MCB）、文献[18]中分布式决策机制（Distributed Policy based Controller Load Balancing，DPCLB）、文献[21]中非合作博弈迁移机制（Non-cooperative game migration mechanism，GAME-SM）等机制的性能. MCB通过控制器备份池应对流量的激增. DPCLB考虑多个负载代价，通过贪婪算法进行优化求解；GAMESM基于非合作博弈的交换机迁移算法以动态平衡控制平面负载. 实验分别验证了网络通信开销、流表建立时间、流表平均建立时间和控制器资源利用率等性能.

网络通信开销情况如图4所示，通信总开销为控制器与控制器之间的通信开销和控制器与交换机之间的通信开销总和. 从控制器的通信开销方面看，GAME-SM是最高的，MCB位居第二，DPCLB和GTLB相差不大；从控制器与交换机自己的通信开销来看，MCB是最大的，GAME-SM开销较高，DPCLB和GTLB差别不大. 因此，在实现负载均衡的基础上，GTLB机制的总通信开销最少，它相较于MCB、DPSLB、GAME-SM分别减少39.2%、5%、20.8%.

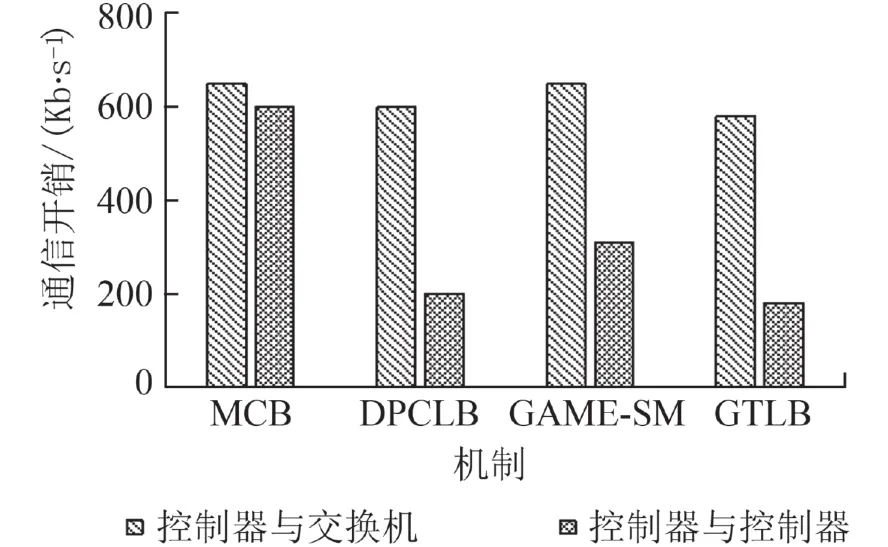
图4 控制器与交换机及控制器之间的通信开销Fig. 4 Communication overhead between controller and switch and controller

流表建立时间动态反映控制器负载的情况，它的情况如图5所示. MCB和GAME-SM波动明显.DPCLB和GTLB波动较小，GTLB划分不干扰GPF，设置了控制器的倒计时数，避免了迁移冲突，GTLB的流表建立时间低于其它3种机制.

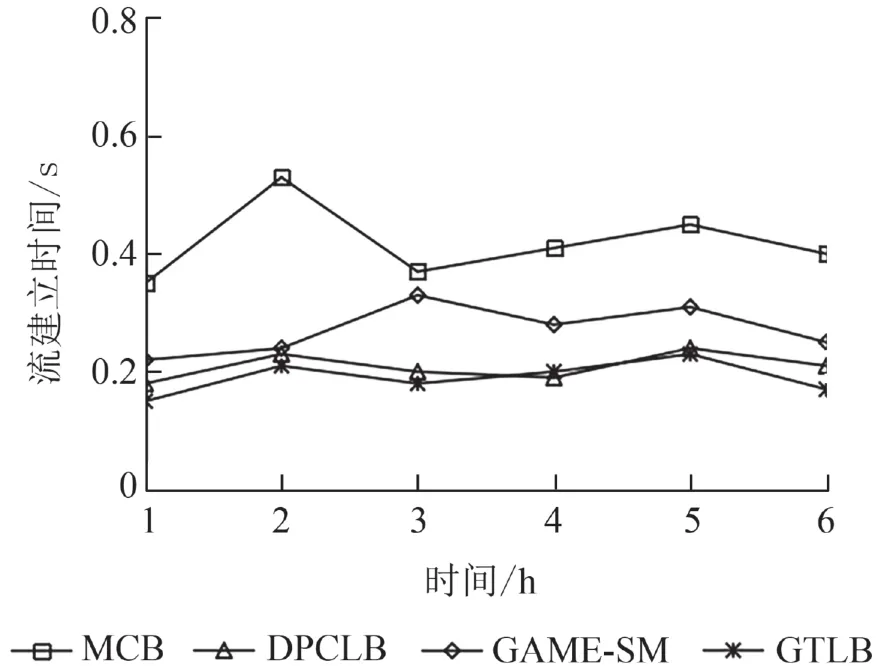
图5 交换机流表建立时间Fig. 5 The setup time of switch flow table

流表平均建立时间通过对图5中的实验结果进行量化统计得到，如图6所示. GTLB机制的流表平均建立时间相较于MCB、DPCLB、GAME-SM分别下降57.1%、14.3%、33.3%，平均缩短了0.12 s.

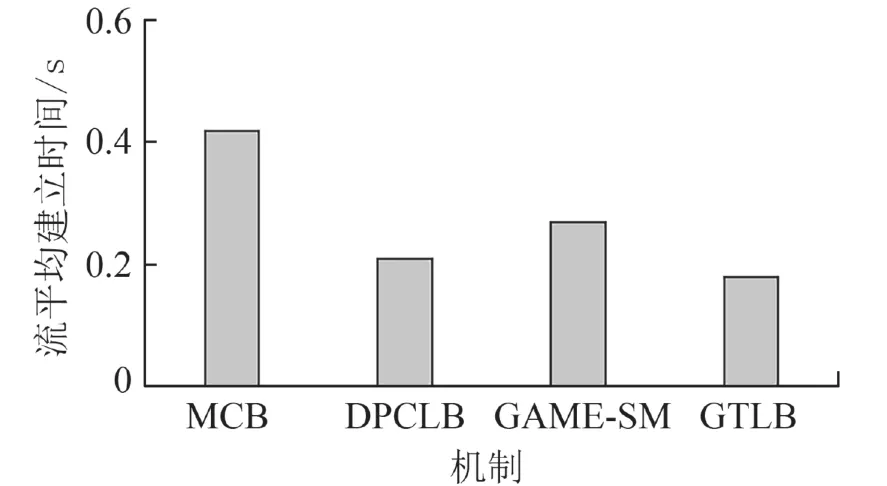
图6 交换机流表平均建立时间Fig. 6 The setup time of average switch flow table

控制器资源利用率反映控制器负载的利用情况，利用率越高，控制器负载均衡性能越好. 如图7所示. GAME-SM最低，MCB较低，DPCLB和GTLB相差不大，都能较好地实现控制器负载均衡和高效地资源利用，但GTLB部署了更少的控制器，控制器资源利用率提高了20.4%. 因此，GTLB控制器负载均衡性能最佳.

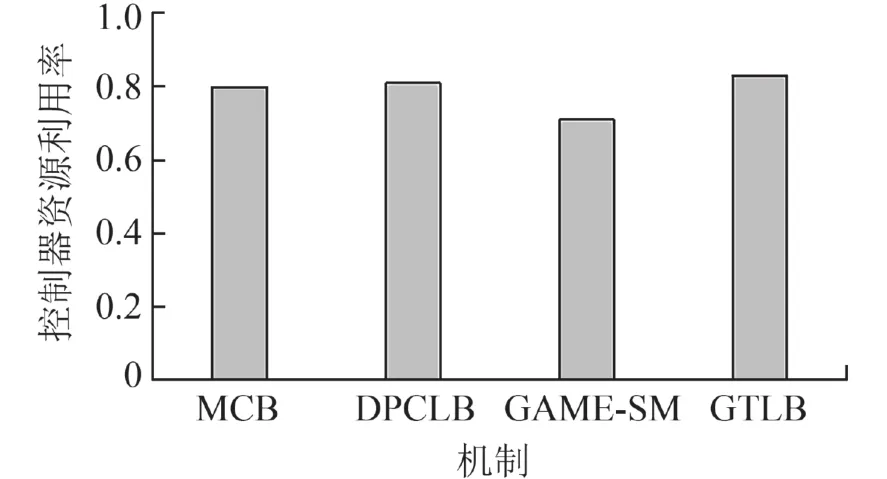
图7 控制器资源利用率Fig. 7 The utilization of controller resource

5 结论

针对SDN 的控制器负载均衡问题，本文提出了基于博弈论的SDN多控制器负载均衡机制，优化了控制器负载的动态均衡. GTLB机制结合交换机迁移，构建博弈域模型，通过3个阶段实现了交换机的协调迁移和控制器的角色转换. 与其他机制相比，GTLB降低了网络的总通信开销，流建立时间平均缩短了0.12 s，控制器资源利用率提高了20.4%，控制器负载更为均衡. 今后的工作将集中在研究控制器博弈的最佳门限和解决粒子群算法后期收敛性差、易陷入局部最优解的问题.