可再生能源消纳责任权重制下电力市场优化决策模型

林晓凡，曾佳妮，冯冬涵

（1. 上海交通大学电子信息与电气工程学院，上海市200240；2. 电力传输与功率变换控制教育部重点实验室，上海交通大学，上海市200240）

0 引言

2020 年1 月，随着中国可再生能源消纳责任权重制（renewable portfolio standards，RPS）的正式施行，电力用户将作为RPS 义务主体以实际消纳可再生能源电力为主要方式完成可再生能源消纳责任权重指标并接受年度考核。同时随着电力现货市场的建设，多数电力市场都采用了集中式的全电量现货市场模式，发电机组的实际出力计划将遵循日前市场和实时市场综合形成的出清结果。随着可再生能源（renewable energy，RE）发电成本的不断下降和出力预测精度的提升［1-2］，RE 将逐步进入电力现货市场与常规能源同台竞价，其具有的环境友好属性与出力不确定性、波动性将给电力现货市场带来许多变数，因此研究RPS 背景下含有RE 发电商的电力现货市场具有重要意义。

目前国内外学者关于RPS 及其与电力市场联动的研究主要为以下2 个方面。一是RPS 框架体系及其有效性。文献［3］利用系统动力学的方法研究RPS 对中国电源结构的影响机理及效果，结果表明RPS 可以有效地促进中国电源结构调整，达到政府政策目标。文献［4］提出了RPS 下绿色电力证书（以下简称绿证）补偿辅助服务的方案，提出将辅助服务量化为一定量的绿证以激励辅助服务提供商为RE 消纳提供服务的积极性。文献［5］设计了以电力用户为义务主体的RPS 框架并论证了其可行性。文献［6-8］分析对比了国外多种RE 扶持政策并对中国RPS 框架提出建议。二是RPS 背景下电力市场多主体交易策略的研究。文献［9-12］建立了绿证交易的电力市场均衡模型，并分析了RPS 对RE 电力消纳的促进作用和市场特征，但将义务主体设置为发电侧。文献［13-16］建立了以电力用户为义务主体的中长期电力市场最优决策模型，分析了RPS 考核权重指标对于电力市场出清结果及市场主体报价的影响。文献［17-22］建立了RE 发电商收益最大化的均衡约束数学规划问题（mathematical planning problem with equilibrium constraints，MPEC），通过强对偶定理、二进制拓展法等线性化手段将其转化为混合整数线性规划（mixed-integer linear programming，MILP）模型进行求解。

综上所述，目前关于RPS 与电力市场的研究很少是基于以电力用户为义务主体且实际消纳RE 电力也算作消纳量这一背景，故本文在梳理分析中国RPS 框架内容的基础上，建立了包含RE 发电商的多时段、多场景电力现货市场多主体双层优化决策模型，通过库恩-塔克（Karush-Kuhn-Tucker，KKT）条件、强对偶定理等手段将其转化为单层MILP 模型，利用对角化算法求取市场均衡点，分析RPS 考核权重指标、绿证价格、RE 功率渗透率对于市场均衡点的影响。

1 RPS 下电力市场架构

1.1 电力市场架构

RE 中风电、光伏发电最先纳入绿证核发对象，对每1 MW·h 实际发电量核发一个绿证，风电、光伏发电商可以通过售卖绿证获得额外的收益；承担RPS 的电力用户以实际消纳RE 电力为主要完成方式，同时可通过向超额完成年度消纳量的市场主体购买其超额完成的RE 电力消纳量或购买绿证2 种方式来完成消纳量。故对于电力用户来说，有3 种方式可以获取消纳量。一是在电力市场当中购买RE 电力，对应成交量可登记为电力用户的消纳量。二是在超额消纳量市场当中购买其他电力用户超额完成的消纳量指标。三是在绿证市场中购买绿证，绿证对应的RE 电量可等量记为消纳量。

电力现货市场中电能量市场一般包括日前、实时市场，但由于电力用户实际消纳RE 电力可算作消纳量使得在市场出清结算时RE 电力需要一对一确定消纳方，而日前市场集中竞价无法确定RE 电力的消纳方。采用集中撮合竞价虽然可以一对一确定RE 电力消纳方，但高低报价匹配的原则无法体现电力用户为获取消纳量而需付出额外代价且违背市场规律。针对这个问题，文献［23］提出了增设RE电力日前交易市场的解决办法，在日前市场中将RE电力与常规能源电力分开交易，RE 电力日前交易市场中采取挂牌方式一对一确定消纳方。本文假设的RPS 下电力市场架构如图1 所示，包含RE 日前市场、常规能源日前市场、实时市场、绿证市场、超额消纳量市场5 个市场。市场组织时序按RE 日前市场、常规能源日前市场、实时市场依次开展，绿证、超额消纳量市场执行单独的市场组织时序。

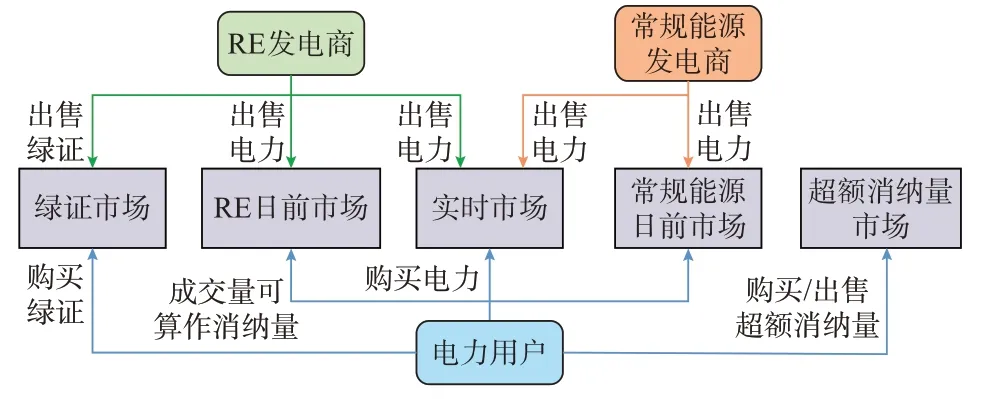
图1 RPS 下电力市场架构图Fig.1 Structure diagram of electricity market under RPS

1.2 市场模型假设

本文提出的模型包含RE 日前市场、常规能源日前市场、实时市场、超额消纳量市场和绿证市场，其中超额消纳量市场和绿证市场交易标的物皆为具有金融属性的指标量，二者对于完成RPS 考核要求作用相同且电力用户可自由选择参与交易，故在模型中假设超额消纳量与绿证二者价格相同。

市场主体包括RE 发电商、常规能源发电商、电力用户，其中RE 发电商与电力用户为策略报价者，常规能源发电商为非策略报价者。市场出清模型中线路模型为考虑线路阻塞的直流潮流模型，发电商与电力用户均考虑出力上、下限限制。在日前与实时市场中，每个时间段发电商与电力用户都需要提交多段发/用电容量与报价，发电商的分段报价单调递增，电力用户的分段报价单调递减；在实时市场中，RE 电力与常规能源电力一视同仁进行出清。对于RE 发电机组考虑其出力的不确定性与波动性，通过在实时市场中设置多场景来模拟RE 预测出力与实际出力的偏差，对于电力用户考虑其负荷的波动性，负荷最大值随时间变化。RE 发电商在RE 日前市场与实时市场出清结束后可能出现2 个市场出清量存在偏差的情况，若为正偏差，即实时市场出清量大于RE 日前市场出清量，则RE 发电商获得偏差量对应的绿证；若为负偏差，则RE 发电商需要向RE 日前市场中对应的电力用户补交付偏差量对应的绿证［23］。

在RE 日前市场中采取挂牌交易模式，故RE 日前市场的结算电价为RE 发电商的报价，本模型中电力用户在RE 日前市场的报价为摘牌意愿价。常规能源日前市场与实时市场为集中竞价且采用节点电价进行结算，日前市场与实时市场的出清电量偏差量根据实时市场节点电价进行结算。

2 电力现货市场多主体优化决策模型

本文电力现货市场多主体优化决策问题为双层模型，如图2 所示。上层为策略报价者利润最大化模型，求解得到策略竞价者最优报价传递给下层模型；下层为RE 日前市场、常规能源日前市场、实时市场出清模型，求解得到节点电价、各主体出清电量返回上层模型。

2.1 双层决策模型

2.1.1 上层模型1:RE 发电商利润最大化

对RE 发电商i，其最优决策模型如下式所示:

图2 电力现货市场双层决策模型Fig.2 Bi-level decision model for electricity spot market

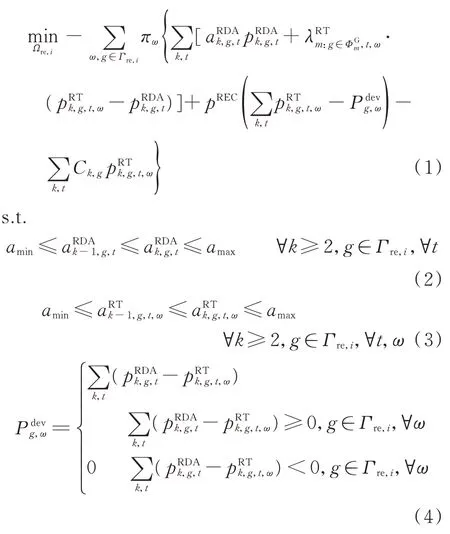
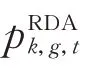
2.1.2 上层模型2:电力用户利润最大化

对电力用户j，其最优决策模型如下所示。

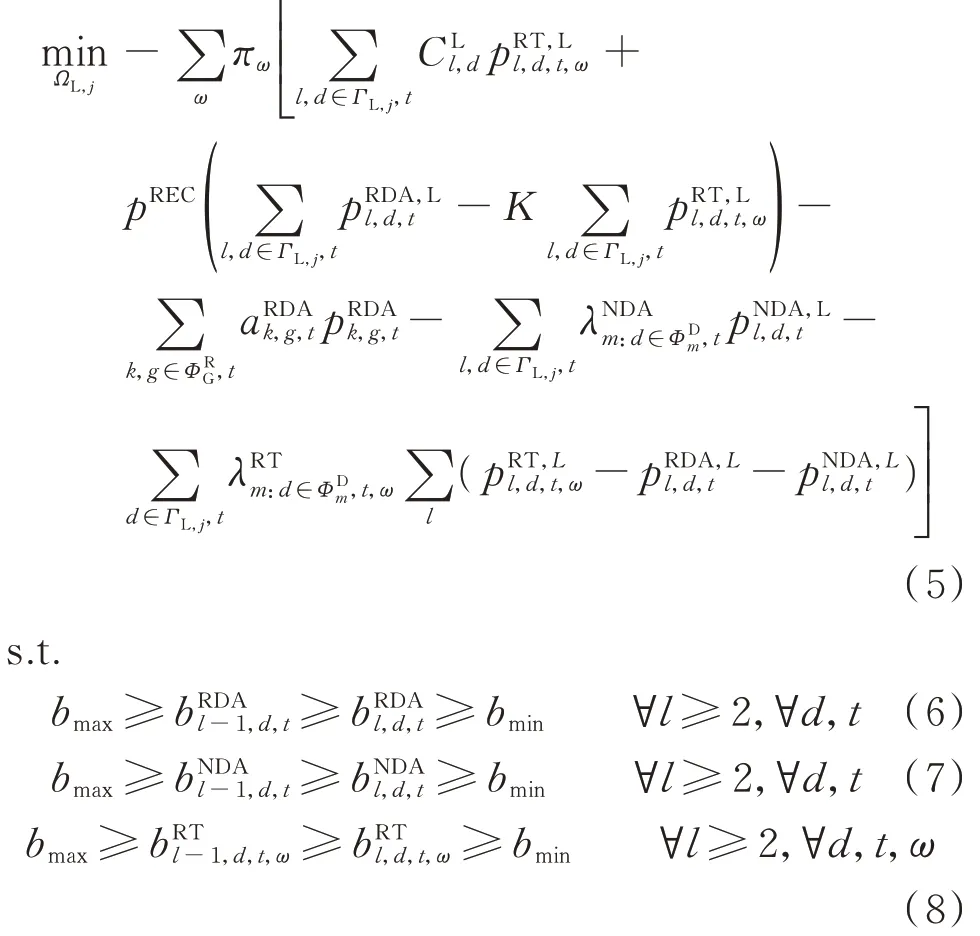
2.1.3 下层模型3:RE 日前市场出清

RE 日前市场出清模型如下所示。

目标函数（9）最小化RE 日前市场负社会福利。约束（10）确保每个节点功率平衡；约束（11）、（13）限制RE 发电机组出力和负荷不超过分段功率上、下限；约束（12）限制RE 发电机组在RE 日前市场中标容量不超过RE 日前预测出力；约束（14）确保线路潮流不超过容量上限；约束（15）限制节点相角不超过上、下限；约束（16）选择节点1 作为参考节点。

2.1.4 下层模型4:常规能源日前市场出清

常规能源日前市场出清模型如下所示。

目标函数（17）最小化常规能源日前市场负社会福利。约束（18）确保每个节点功率平衡；约束（19）、（20）限制常规能源发电机组出力和负荷不超过分段功率上、下限；约束（21）确保线路潮流不超过容量上限、约束（22）限制节点相角不超过上、下限；约束（23）选择节点1 作为参考节点。

2.1.5 下层模型5:实时市场出清

实时市场出清模型如下所示。

目标函数（24）最小化实时市场负社会福利。约束（25）确保每个节点功率平衡；约束（26）、（28）限制发电机组出力和负荷不超过分段功率上、下限；约束（27）限制RE 发电机组在实时市场中标容量不超过实时预测功率；约束（29）确保线路潮流不超过容量上限；约束（30）限制节点相角不超过上、下限；约束（31）选择节点1 作为参考节点。

2.2 双层决策模型转化为MILP 原理

对于双层优化模型的求解，一般先利用下层模型的KKT 条件［24］将双层模型转化为等价的单层MPEC，再利用强对偶定理［25］、二进制拓展法［26］等手段将其转化为MILP 模型进行求解［27］。

2.2.1 模型（3）的KKT 条件

模型（3）的KKT 条件由式（10）、式（16）、式（32）至式（42）组成。

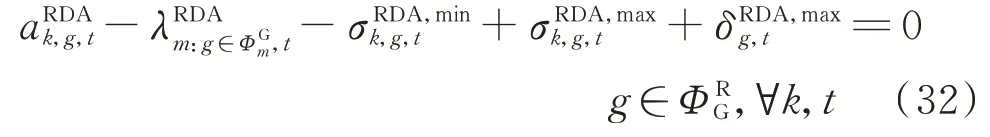
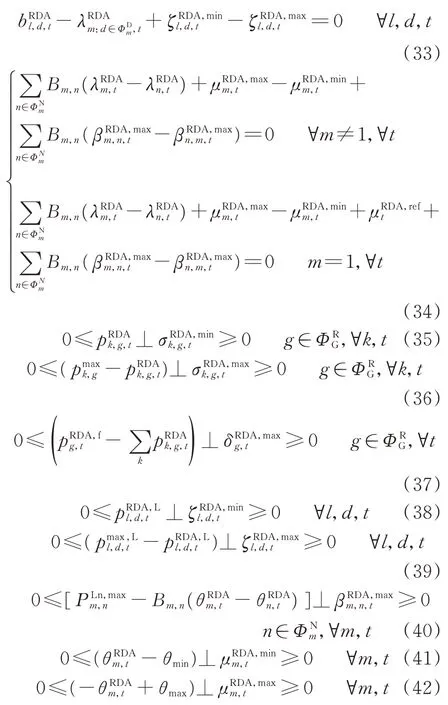
式中:⊥为互补约束运算符。

2.2.2 模型（4）的KKT 条件

模型（4）的KKT 条件由式（18）、式（23）、式（43）至式（52）组成。

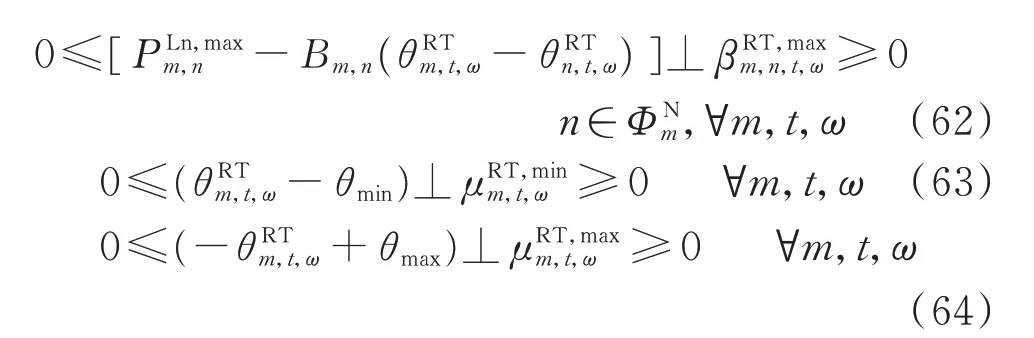
2.2.4 MPEC 转化为MILP

对于RE 策略报价发电商，其MPEC 由目标函数（1），以及约束条件（2）至（4）、式（32）至式（64）组成。

对于策略报价电力用户，其MPEC 由目标函数（5），以及约束条 件（6）至（8）、式（32）至式（64）组成。

MPEC 为非线性问题，导致其非线性有以下3 个原因，对其线性化处理后可转化为MILP 进行求解。

由式（53）和式（65）可得:

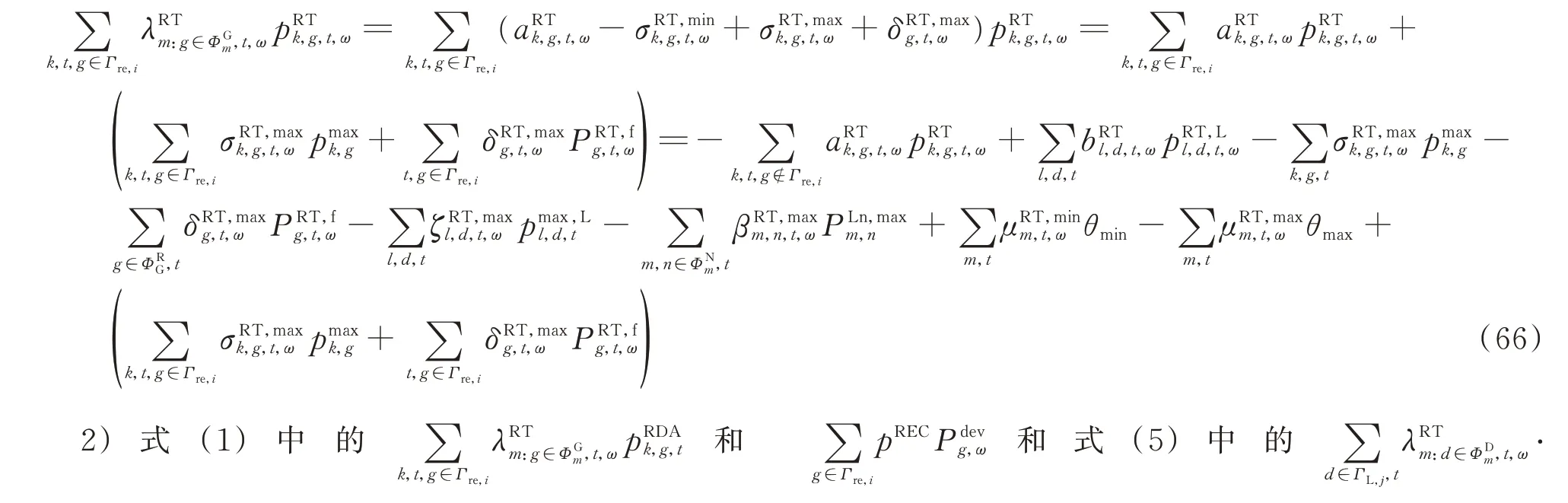
3）MPEC 中含有大量的非线性互补约束（35）至（42）、（46）至（52）、（57）至（64），其 形 式 为0 ≤H ⊥Q ≥0，可用大M 法［28］对其进行线性化并得到如下结果。

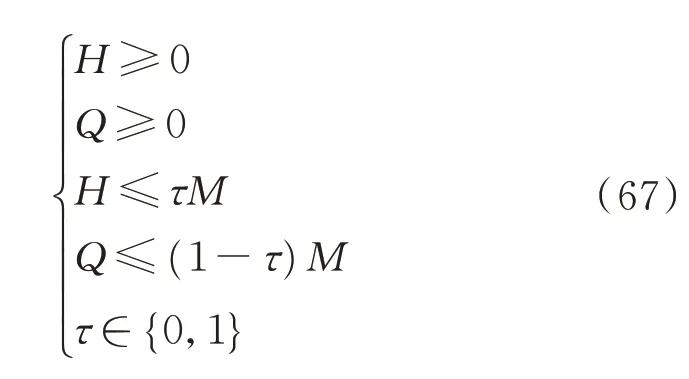
式中:M 为常数，取值为相对于H 和Q 较大的数；τ为二进制变量，取值为0 或1。

通过对MPEC 采取以上线性化操作后，将MPEC 转 化 为MILP，可 以 使 用Gurobi、CPLEX 等商业求解器高效求解。

3 对角化算法

本文采用对角化算法［29］对市场均衡点进行求解，对角化算法通过迭代求解各个策略报价主体的MILP 来得到最优报价策略，终止条件为所有主体本轮报价与上一轮报价差值处于可接受范围内，同时设置最大迭代次数，若达到最大迭代次数仍未收敛，则输出“未收敛至市场均衡点”并调整各策略主体初始报价重新计算市场均衡点。RE 日前市场为挂牌交易模式且电力用户在RE 日前市场摘牌可获得RE 电力和等量消纳量，因此本算法在迭代过程中设置电力用户在RE 日前市场报价为上一轮电力用户在常规能源日前市场结算电价加上绿证价格，代表电力用户摘牌RE 电力的意愿报价。图3 为对角化算法迭代求解流程图。其中nmax和mall分别为最大循环次数和全部策略报价者数量。

当MILP 问题规模较大时给求解带来了困难，对此可从2 个方面做进一步优化调整。一是利用启发式算法确定各策略主体初始报价；二是策略主体在其他主体报价不变基础上确定自身最优反应时，可利用并行计算加快求解速度。

4 算例分析

4.1 算例参数

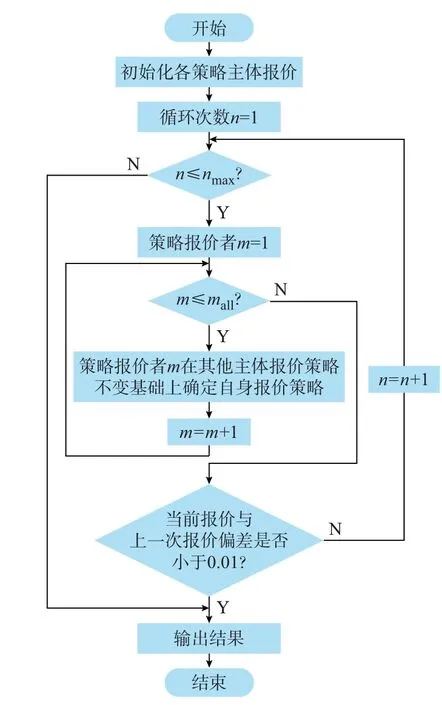
图3 对角化算法流程图Fig.3 Flow chart of diagonalization algorithm

基于上述提出的模型，假设在如附录C 图C1 所示的经修改的IEEE 14 节点系统上有G1 至G7 这7 个 发 电 机 组 和D1 至D3 这3 个 负 荷，其 中G2、G4为风电机组，分别属于RE 发电商1 和RE 发电商2；G1、G3、G5、G6、G7 分别属于常规能源发电商1、发电商2、发电商3、发电商4、发电商5；D1 至D3 负荷属于电力用户1。发电机组和负荷参数见附录C表C1。

考虑运算效率与模型复杂度，本文设置4 个场景8 个时段来模拟1 d（24 h）的电力现货市场交易，每个时段包含3 h。基于Elia 能源公司的历史风电数据［30］，利用K-means 聚类方法得到风电出力的典型曲线与概率并组合成多场景出力，风电机组出力和负荷曲线分别如图4 和图5 所示，图中出力采用标幺值。

4.2 RPS 考核指标及绿证价格对市场均衡点的影响

为探究RPS 考核权重指标K 对市场均衡点的影响，本文设置K 从0.05 至0.40 以步长0.05 递增，对这8 个场景求解得到的市场均衡点分析发现，K的变化对于市场均衡点处3 个市场的出清结果和策略报价主体的报价策略没有影响，但由于电力用户需要购买更多相比常规能源电力价格更高的RE 电力或绿证、超额消纳量，因此电力用户的利润呈现较为明显的下降，K 从0.05 变化至0.40 时，电力用户利润下降了8%。

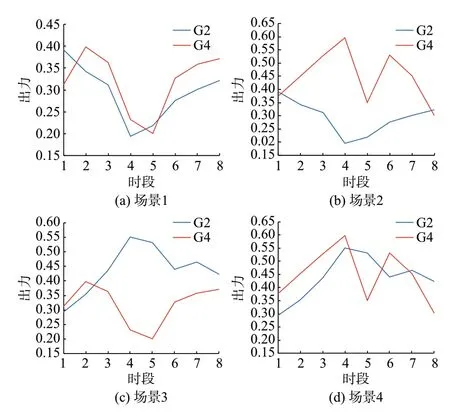
图4 风电机组多场景出力Fig.4 Power outputs of wind turbines in multiple scenarios

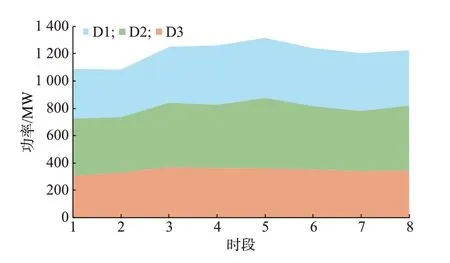
图5 负荷曲线Fig.5 Load curves

在探究绿证价格pREC对市场均衡点影响中，本文设置pREC从100 元/（MW·h）至140 元/（MW·h）以步长10 元/（MW·h）递增，随着绿证价格的提高，RE 日前市场出清电价随绿证价格呈现相同的增长趋势，具体数据见表1。基于对市场主体报价策略的分析以及对RPS 规则的理解，RE 电力相比常规能源电力附加了环境友好属性并通过绿证使其货币化，电力用户在RE 日前市场购买RE 电力可提前锁定消纳量，故在成本相同的情况下电力用户更倾向于购买RE 电力，呈现在市场均衡点的表现为RE 日前市场出清电价等于常规能源日前市场出清电价加上绿证价格。

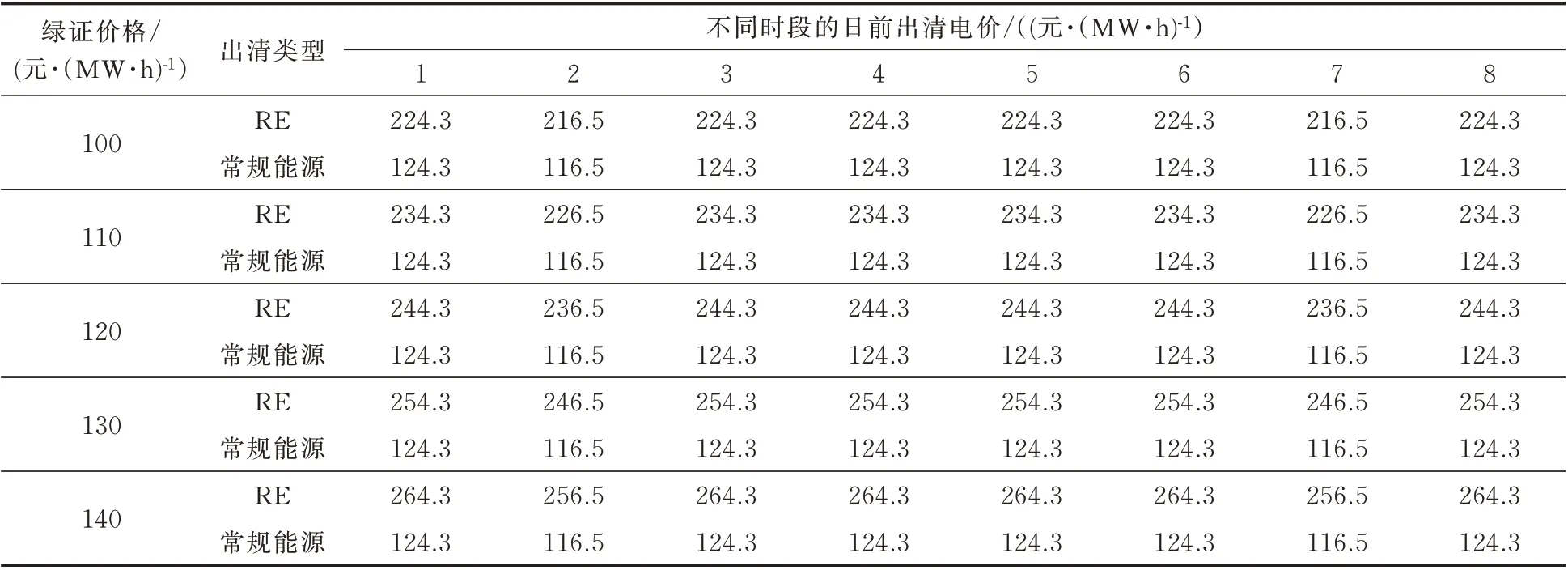
表1 不同绿证价格下日前市场出清电价Table 1 Clearing price of day-ahead market with different green certificate prices

4.3 RE 功率渗透率对市场均衡点的影响

随着RE 产业的发展，RE 装机容量将进一步提高，因此有必要研究RE 功率渗透率对于电力现货市场的影响。附录C 表C1 为RE 功率渗透率为20%时的参数，本文设置RE 功率渗透率从5%至35%以步长5%递增，即G2、G4 机组装机容量分别从70.0 MW 和87.5 MW 递 增 至490.0 MW 和612.5 MW，其他参数保持不变。电力现货市场平均出清电价随RE 功率渗透率的变化如图6 所示，与4.2 节相同的是，RE 日前市场出清电价等于常规能源日前市场出清电价加上绿证价格，故其与常规能源日前市场出清价变化趋势相同。

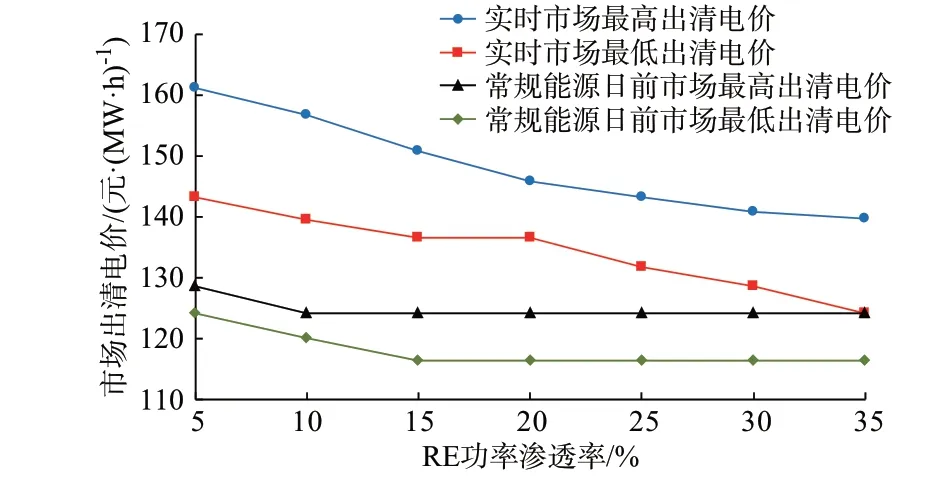
图6 RE 功率渗透率对市场出清电价的影响Fig.6 Influence of RE power penetration on market clearing price

随着RE 功率渗透率的增长，3 个市场出清电价皆呈现下降趋势，其中实时市场出清电价下降程度要大于日前市场，降低了13.3%，而日前市场出清电价下降了3%。当RE 功率渗透率达到35%时，由于RE 出力波动绝对值增大，在运行日内实时市场最低出清电价与常规能源日前市场最高出清电价相等。

5 结语

本文基于RPS 框架建立了包含RE 日前市场、常规能源日前市场、实时市场的电力现货市场多主体双层优化决策模型，通过强对偶定理、二进制拓展法等方法将其转化为MILP 模型求解市场均衡点。通过算例分析了RPS 考核权重指标K 及绿证价格对市场均衡点的影响，单纯K 的改变并不会影响市场均衡点的出清电价和报价策略，在实际情况中，K的改变会引起绿证和超额消纳量供需关系发生变化，从而通过改变绿证价格间接对市场均衡点产生影响。同时研究发现，RE 日前市场出清电价在市场均衡点将等于常规能源日前市场出清电价加上绿证价格，这正是RE 电力正外部性（对环境友好）货币化的体现。

随着RE 功率渗透率的提高，电力现货市场出清电价呈现下降趋势，其中实时市场下降程度比日前市场更大。RE 功率渗透率的提高同时增大了发电侧出力的波动性和不确定性，应从2 个方面予以应对。一是建立适应RE 发电特性的偏差电量考核机制，激励RE 发电企业提高发电预测水平，利用储能等技术平抑出力的波动性；二是完善电网调峰、调频等辅助服务市场机制，提高系统灵活性调节能力。未来还将基于本文双层决策模型加入绿证、超额消纳量市场竞争、发电机组投资决策、年度消纳量指标实时完成情况等因素做进一步研究。

本文受到国家自然科学基金资助项目（51677115）和上海交通大学晨星优秀青年学者奖励计划资助，特此致谢。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。