考虑现货市场竞价空间的梯级水电站中长期合同电量分解模型

于旭光，李亚鹏，贾泽斌，李 刚，程春田，曹 瑞

（1. 大连理工大学水电与水信息研究所，辽宁省大连市116024；2. 大连市清洁能源高效利用重点实验室，辽宁省大连市116024）

0 引言

2019 年6 月底，随着蒙西电力现货市场启动模拟试运行，全国首批8 个电力现货市场建设试点全部进入试运行阶段，标志着中国电力市场化改革迈上了新的台阶［1-3］。目前，现货模式下的中长期合同以电能量为标的［4-5］，分为2 种:第1 种采用差价合同，不需要物理执行，依据日前现货市场价格进行差价结算，现货电能量市场采用全电量竞价模式［6-7］；第2 种采用物理合同且需要物理交割，分解至运行日执行，偏差采用金融结算，现货电能量市场则采用部分电量竞价模式［8-9］。针对第2 种需要物理执行的中长期交易合同，如何科学合理地将其分解为可执行电力曲线并与现货市场平稳衔接是亟待解决的关键问题之一。

关于合同电量分解问题，已有一系列相关研究，从市场运营者分解角度，已有文献主要集中于各类分解目标［10-17］和算法［18-24］。

1）目标方面:文献［10］将月电量竞价空间滚动均衡化作为目标，以降低电网购电费用；兼顾电网调度公平性和经济性，文献［11］提出了适应不同竞价模式的合同电量编制与分解方法；为充分考虑分解个体差异，文献［12-13］分别基于主体满意度和期望分解曲线进行模型构建；为尽量保证合约电量完成进度一致，文献［14-17］以机组间合同电量完成进度偏差最小为优化分解目标。

2）算法方面:文献［18-19］采用确定性分解算法，按机组可发容量等比例分配，操作灵活简便，文献［20］在此基础上引入滚动修正分解策略。采用启发式算法，文献［21-22］分别提出了基于电荷系统搜索和粒子群优化的合同分解方法。文献［23-24］应用数学规划类方法，前者以平均负荷率为标准将合同分解问题转化为二次规划问题，后者计及电价波动风险构建了机会约束规划模型。从市场主体分解角度，已有研究涉及不同市场电量的划分［25］以及发电效益与风险［26-29］。以梯级水电站发电效益最大为目标，文献［26］研究了年度合约电量的确定与分解，文献［27］考虑了发电流量和电价的不确定性，定量分析了效益与风险，文献［28-29］则建立了基于风险偏好的合同电量月度分解模型。

上述文献中研究对象涉及火电居多，关于水电站合同分解，多侧重于梯级水电站发电效益，鲜有站在市场运营角度考虑与现货市场衔接的梯级水电站合同分解研究。为此，本文在上述研究的基础上，针对水电富集电力市场，为缓解现货市场电价的剧烈波动，促进市场的平稳运行，建立了基于各流域梯级水电站间合同分解公平性，以余留现货竞价空间尽量均衡化为目标的中长期合同电量分解模型。该模型考虑了梯级水电站间紧密的水力和电力联系以及合同电量的执行要求，并采用多项式拟合技术处理模型中多变量耦合非线性关系，将月尺度合同电量分解至日尺度。以中国西南地区水电富集的云南电力市场为背景，选取澜沧江和金沙江梯级水电站进行算例分析，结果表明该模型能够合理分解各流域梯级水电站中长期合同电量，并为现货市场余留均衡化的竞价空间，以期为市场运营机构分解提供决策支持，也可提供给市场主体作为其自行协商分解的参考方案。

1 问题描述与建模

1.1 问题描述

由市场主体协商分解能够避免由第三方机构分解所带来的公平性问题［30-31］，但市场主体获取的市场全景信息有限，更无法考虑市场主体间的协调联系。分解方案一方面难以实现系统整体优化，另一方面也可能无法满足系统或电网运行要求，不能充分执行的风险较大，反而违背了市场主体协商分解的初衷。相比较而言，市场运营机构可掌握更全面的电网和市场数据信息，包括系统负荷、电网架构、机组运行情况等，为实现全局优化创造了条件，也使其给出的分解方案更具可行性。例如，水电富集的电力系统往往由多个流域梯级水电站群构成，梯级水电站之间存在极为紧密的水力和电力联系。充分发挥流域梯级水电站以及跨流域协调等作用，可使得整体优化的效益更强，更有利于促进清洁能源消纳。此外，若规则要求市场主体协商分解，亦可以此为参考约定发用电曲线，此时市场运营机构给出的分解方案也具有重要的参考价值。

为此，针对水电富集的电力市场，本文从市场运营机构角度进行合同分解研究，旨在寻求梯级水电站中长期合同科学合理的分解方案。

1.2 目标函数

本文设计的目标函数主要考虑以下2 个方面。

1）考虑到电力商品的物理特征，现货市场的价格信号往往会随着不同时段、不同区域供需关系的剧烈变化而频繁变动［3］。在水电富集的市场中，受天然来水的不确定性影响极大，这使得供给侧的发电能力在各天之间甚至一天之内都可能出现很大的波动。供给侧、需求侧的波动相叠加，使其市场价格波动风险远高于其他市场，剧烈波动的电价信号将对用户稳定生产、市场平稳运行带来巨大挑战。针对水电富集的电力市场，本文试图通过中长期合同的优化分解，在将电量合同分解为可执行电力曲线的同时，降低余留负荷曲线的波动，使得分解后余留现货市场的竞价空间各时段间尽量均衡，从而在一定程度上缓解现货市场电价的剧烈波动，释放稳定的价格信号，以利于现货市场的稳定运行。其示意图如图1 所示。

图1 中长期合同分解与现货市场的关系示意图Fig.1 Schematic diagram of relationship between medium-and long-term contract decomposition and spot market

2）公平性与市场主体利益息息相关，采用第三方机构进行分解需充分考虑利益主体间的公平性。对于梯级水电站的合同分解，若以单一电站的公平性为目标，单纯地追求各电站之间的公平性，则难以挖掘并实现梯级上下游之间联合优化调度所带来的库容补偿效益，特别是针对梯级内有较好调节性能水库的梯级水电站群。因此本文选取的公平尺度为梯级水电站，且假设各梯级水电站均归属同一业主。

综合以上2 个方面的分析，本文兼顾各梯级水电站之间的公平性，以中长期合同分解过后的余留现货竞价空间尽量均衡化为优化目标，表达式如下:

式中:F 为各梯级水电站对于竞价空间调整程度之和；αi为梯级水电站i 的调整竞价空间的权重；I 为系统内梯级水电站个数；fi为梯级水电站i 对于竞价空间波动程度的调整水平，采用方差表示；T 为分解周期时段总数；Pt为t 时段由预测得到系统总负荷扣除系统内火电、风电、光伏电、部分水电等所占空间后得到，作为对应梯级水电站的模拟负荷；Bi，t为t 时段仅由梯级水电站i 对系统负荷调整之后的余留负荷；Ji为 梯 级 水 电 站i 内 的 电 站 个 数；pi，j，t为 梯 级 水 电站i 第j 个电站在t 时段分解的合同电量对应的出力。上述负荷或出力单位为GW。此外，本文暂未考虑负荷预测误差、可再生能源出力随机性和波动性等问题，以聚焦寻求确定性条件下与现货市场衔接的梯级水电站中长期合同电量分解方法。

1.3 约束条件

1）负荷平衡约束

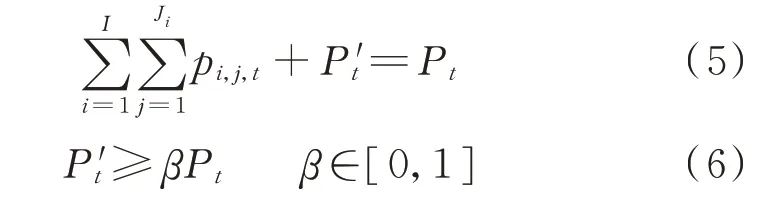
式中:P't为系统内t 时段余留现货市场竞价空间，单位GW；β 为余留竞价空间控制系数，用来控制余留竞价空间的下限。

2）水量及流量平衡约束

式 中:Ii，j，t，Oi，j，t，Qi，j，t，Si，j，t，qi，j，t分 别 为 梯 级 水 电 站i第j 个电站在t 时段的入库流量、出库流量、发电流量、弃水流量、区间流量；Vi，j，t表示梯级水电站i 水库在t 时 段 末 的 库 容；Ωi，j为 梯 级 水 电 站i 第j 个 电 站 的直 接 上 游 水 库 集 合，对 于 龙 头 水 库Ωi，j为 空 集；Qu，t和Su，t分别为上游水库u 在t 时段的发电流量和弃水流量；Δt 为时段步长。

3）发电流量约束

4）出库流量约束

5）水位约束

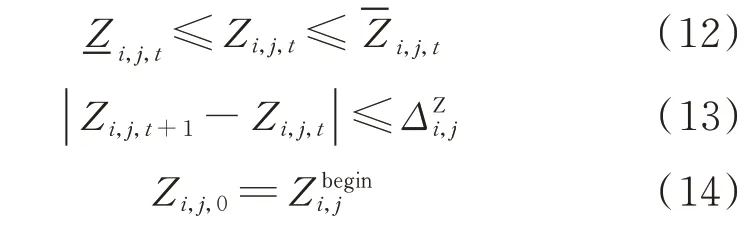
式 中:Zi，j，t，i，j，t，-Zi，j，t分 别 为 梯 级 水 电 站i 第j 个 电 站在t 时段末的上游水位及其上、下限，单位m；Δ为梯级水电站i 第j 个电站允许的水位变幅；Zbegini，j为 其对应水库的月初的实际水位。

6）出力约束

7）合同电量约束

式中:ei，j，t为梯级水电站i 第j 个电站在t 时段分解的合同电量，单位GW·h；Ei，j为梯级水电站i 第j 个电站的月尺度合同电量总电量，单位GW·h；δ 为合同完成的偏差裕度，用来控制各电站之间中长期合同电量具有相近的完成率。

8）发电水头约束

式 中:Hi，j，t，zi，j，t，hloss，i，j，t分 别 为 梯 级 水 电 站i 第j 个 电站在t 时段的发电水头、尾水位、水头损失。本文假定水头损失在调度期内为固定值。

9）水位库容约束

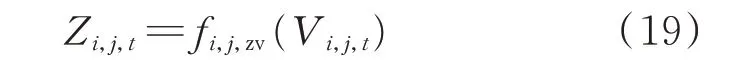
式中:fi，j，zv(⋅)为梯级水电站i 第j 个电站的水位库容关系函数。

10）尾水位泄流量约束

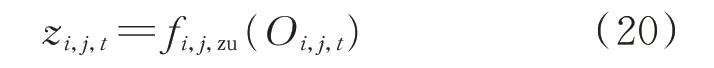
式中:fi，j，zu(⋅)为梯级水电站i 第j 个电站的尾水位泄量关系函数。

11）机组动力特性曲线约束

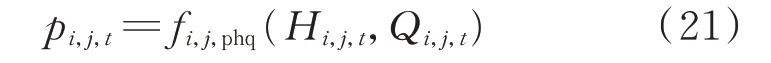
式中:fi，j，phq(⋅)为梯级水电站i 第j 个电站的出力与发电水头、发电流量之间的二元关系。

2 模型求解

第1 章构建的水电富集电力市场环境下梯级水电站中长期合同电量分解模型，属于多变量、高维度、多复杂约束问题，目前其求解方法主要有动态规划及其改进方法［32］、启发式方法［33］及数学规划方法［34］等。动态规划必须满足无后效性原则且当计算规模增加时容易产生“维数灾”问题。启发式方法存在计算时间较长、容易陷入局部最优且计算结果稳定性差等问题，因此本文采用数学规划类方法求解。

水位库容关系是水电机组中典型的非线性函数，为有效保留水电站的实际工程特性，本文基于曲线特征分析，采用多项式描述水位库容关系［35］，并且本文基于多个电站数据，分析衡量计算效率与精度后选取四次多项式来拟合水位库容关系。式（19）可转换为:

式 中:αk，i，j(k=0，1，2，3，4)为 水 位 库 容 拟 合 曲 线参数。

同理采用四次多项式来拟合尾水位泄流量关系。式（20）可转换为:

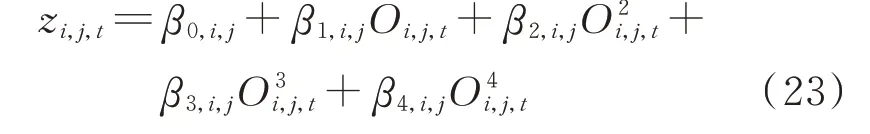
式中:βk，i，j(k=0，1，2，3，4)为尾水位泄流量拟合曲线参数。

针对式（21）采用平均动力特性予以替代，表达式如下:

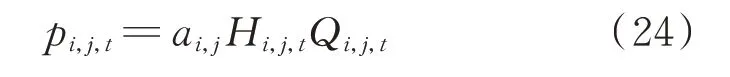
式 中:ai，j为 综 合 出 力 系 数，该 系 数 单 位 为GW/（（m3·s-1）·m）。

综合考虑操作难易、求解效率、结果稳定性等因素，选取成熟的数学规划软件对所提模型进行求解。本文求解工具采用Lingo 软件包［36］，调用以分支定界法为核心的非线性全局优化方法实现模型求解。主要求解思路见文献［35］，更为详细的求解原理和流程见文献［37］。

3 算例分析

3.1 工程背景

本文以中国西南水电富集的云南电力市场为背景。作为新一轮电力市场改革“先锋”，云南在中长期电力市场建设中取得了令人瞩目的成效，交易品种丰富，市场较为活跃，交易量逐年上升，有效促进了清洁能源消纳［38］，正逐步过渡到电力现货市场的建设。同时选取在云南电力市场电厂侧中所占比例较大的澜沧江和金沙江梯级水电站为应用案例，其基本信息和拓扑结构见附录A 和附录B。

3.2 算例设置

水电富集地区的丰水期均面临较高的弃水风险，以防洪安全及水电的大规模消纳为主，各电站接近满载出力，中标交易电量与实际调度之间可调整余地较小，故本文主要研究平枯期合同分解。为验证本文所提模型的有效性，选取2 个场景进行研究:场景1 枯水期和场景2 平水期。

为进一步比较分析，本文针对上述2 个场景均增设了对照组，对照模型仅以余留竞价空间波动最小为目标，不涉及公平性因素，简称对照模型。目标函数表达式如下:

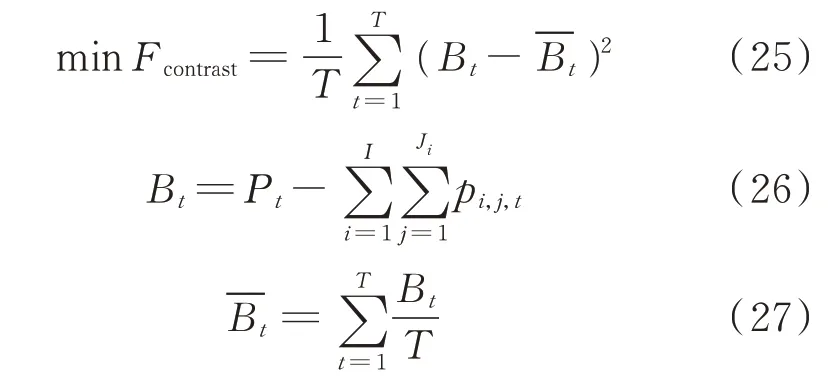
式中:Fcontrast为余留竞价空间波动程度；Bt为t 时段余留的日负荷，即所有梯级水电站对负荷调整之后的现货市场竞价空间；约束条件与本文所提模型相同，即式（5）至式（24），同时输入数据及参数条件均相同，见3.3 节。

3.3 数据及参数选择

负荷以及来水:本文各场景案例中日尺度负荷采用历史数据将总负荷扣除系统内火电、风电、光伏电、部分水电等所占空间后得到，作为对应梯级水电站的模拟负荷。来水选取实际历史资料。

合同电量:中长期待分解的物理执行合同包含优先电量以及通过双边交易或连续挂牌交易竞得的中长期合同电量。

执行约束系数:合同电量执行约束的偏差裕度取3%。

参数:为保证公平性，梯级水电站i 的调整竞价空间的权重αi=1；余留竞价空间控制系数可由市场运营机构基于中长期市场和现货市场的比例控制需求设置，本文取β=0；I=2，J1=5，J2=5；场景1中T =28，场景2 中T =31。

3.4 计算结果

2 种场景下各算例目标函数结果见附录A表A2。

图2 为本文模型及其对比模型在2 个场景中各梯级水电站合同电量分解对应的出力过程以及系统负荷过程图，依次给出了金沙江和澜沧江对于负荷的调整情况，余留日负荷即可表征为余留现货市场竞价空间。另外从图中也可以直观地看出，负荷较高时段分解电量多增大出力，负荷较低时段分解电量少减小出力，使得各梯级水电站整体对于余留竞价空间的调整效果较为显著。

图2 2 个场景下的梯级水电站合同分解过程对比Fig.2 Comparison of contract decomposition processes of cascade hydropower stations in two scenarios

进一步分析图2 以及合同分解数据可知，本文模型在2 个场景下均出现了数天无竞价空间的情形，这是因为本文模型中含有水电运行、合同电量控制约束以及负荷平衡约束。在模型进行优化求解时，不但要求目标函数的最优，还要保证解的可行性。分析调度过程数据可知，竞价空间为0 的几天，恰恰是由于水电运行约束和合同电量约束的控制，使得式（6）成为紧约束（本文β=0），在多约束的联合作用下，出现了无现货竞价空间的情形。而式（6）在对比模型所应用的上述场景中为松约束，从而未出现无竞价空间的情形。上述结果均在对应模型的可行域范围内。

附录B 图B2、图B3 为2 个场景下本文所提模型及对照模型优化计算所得各电站出力和水位过程。场景1 所属枯水期，来水相对较少，各电站出力相对平稳且水位消落相对缓慢；场景2 所属汛前期，小湾和糯扎渡为多年调节水库，水位过程消落到死水位附近，为即将到来的汛期腾库。2 个场景下各算例中各电站的出力、水位等均满足各类运行约束，以满足防洪安全、生态、环境、灌溉、供水等综合利用需求。

合同电量的分配情况见附录A 表A3。2 个场景下各算例中各电站的合同电量和计划分配电量的偏差均位于3%范围内，说明分解结果能够保障合同电量的执行。

综上，本文所提模型及其对比模型均能获得合理有效的合同电量分解结果。针对上述结果的详细分析在3.5 节展开。

3.5 对比分析

1）分析1:响应负荷波动，均衡化余留竞价空间

为量化分析梯级水电站出力过程与系统负荷的响应程度，选取相关性系数［39］来比较2 个时间序列的相关性，结果列于附录A 表A4。相关性系数均大于0.98，说明2 个模型均可以使得各梯级水电站整体分解合同电量对应的出力能较好地跟踪系统负荷曲线的趋势，充分响应负荷波动。

附录A 表A5 展示了2 个场景下各模型对竞价空间调整前后的关键指标。采用本文所提模型优化后，场景1 中负荷峰谷差从9.39 GW 减少至2.75 GW，均方差从2.25 GW 减少到0.86 GW，降幅分别达到了70.71%和61.78%；场景2 中总负荷峰谷差由4.95 GW 降至3.85 GW，均方差由1.67 GW变为1.24 GW，降幅分别为22.22%和25.75%。从对比模型的指标数据上可以看出，场景1 中峰谷差减少为0.07 GW，余留竞价空间对应负荷的均方差变为0.01 GW；场景2 中峰谷差降至0.24 GW，余留竞价空间对应负荷的均方差变为0.07 GW。

通过上述数据分析可知，2 个模型优化计算后，2 个场景下峰谷差和均方差均能得到大幅度减小，对于余留竞价空间的调整效果显著，使得余留竞价空间曲线更加平缓，可为现货市场提供更为均衡化的竞价空间，有利于减缓现货市场电价的剧烈波动。除此之外，对比模型中上述优化指标均不同程度地优于本文模型，对于减缓余留竞价空间波动程度的效果更为显著，说明本文模型兼顾公平性也弱化了对于余留竞价空间的调整能力。

2）分析2:优化合同分解，协调利益主体公平性

2 个场景下各算例中合同执行电量偏差均在3%范围内，一定程度上保障了合同执行度的公平性，从而保证了各梯级水电站间的合同利益。

图3 所示为2 个模型在各场景中澜沧江和金沙江的合同分解对应出力过程对比图。从图中可以看出与对比模型相比，本文模型在2 个场景下的出力曲线趋势更为相近。为进一步衡量不同目标下参与优化的各梯级水电站之间对于余留竞价空间调整水平的公平程度，采用各梯级水电站出力曲线的相似性作为对比指标。本文引入离散Fréchet 距离来衡量各梯级水电站出力过程的相似性。Fréchet 距离与 常 用 的Hausdorff 距 离 相 比，Fréchet 距 离 考 虑 了曲线的形状以及曲线上各点的时序，在刻画曲线相似程度方面具有一定的比较优势［40］。其具体定义如下:

式中:∂F(g，l)为Fréchet 距离；‖ ⋅ ‖为L2范数；g(⋅)和l(⋅)表示[a，b]→R2给定的2 个函数，其中a，b ∈R，且a ＜b；α(⋅)和β(⋅)表示[0，1]→[a，b]的任意连续非递减函数。

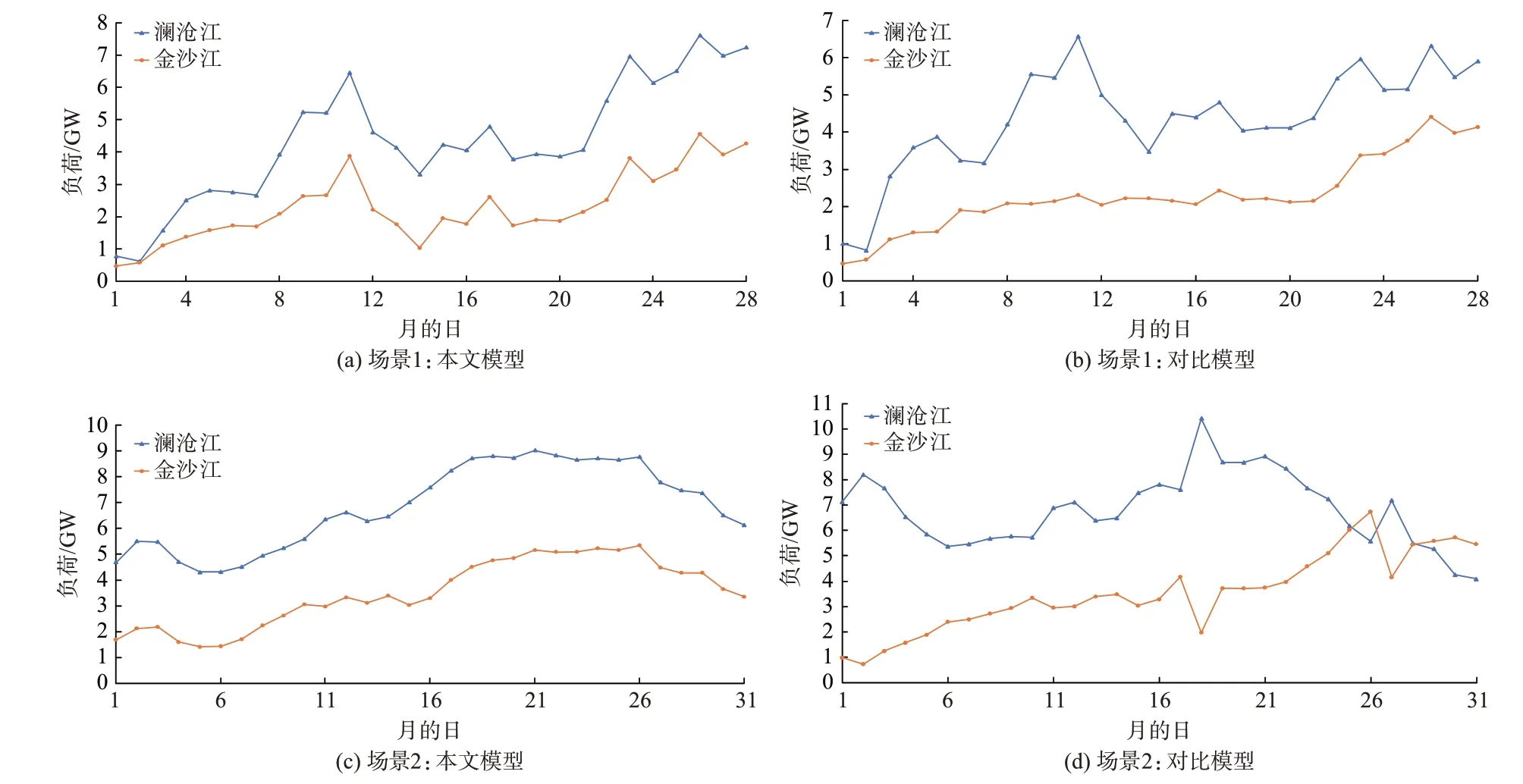
图3 2 个场景下的梯级水电站合同出力过程对比Fig.3 Comparison of contract output processes of cascade hydropower stations in two scenarios

本文对比澜沧江和金沙江梯级水电站之间对于余留负荷调整程度的公平性。由于两者合同总电量不一致，为便于对比，首先采用下式进行归一化处理:

式中:λi，t为梯级水电站i 在时段t 的平均出力占梯级水电站i 所有时段出力之和的比例。基于λi，t在全周期内的离散点形成澜沧江和金沙江2 条曲线，采用离散的Fréchet 距离［41］来衡 量2 个梯级水电 站之间各日出力占比曲线的相似性。

计算结果列于附录A 表A6，从中可看出场景1和场景2 中本文模型所得2 个梯级水电站出力占比曲线的离散Fréchet 距离分别为0.011 和0.007 8，与对比模型的0.017 8 和0.035 2 相比均更小，且相差较大。说明，对比模型偏离理想的公平结果（Fréchet 距离为0）更远，很大程度上破坏了系统内梯级水电站之间对于余留竞价空间调整程度的公平性，出力曲线相似性较差；而本文模型所得结果中2 条曲线更为相似，能够通过优化合同分解出力过程，更好地协调好利益主体间的公平性。

综合上述对比分析，中长期合同电量分解过程中，市场利益主体间的公平性目标与余留竞价空间尽量均衡化目标之间存在着一定的负相关关系，合同分解兼顾公平性对分解结果影响较大，在市场化环境下是一个不能忽视的因素。

通过以上多场景多案例的结果以及对比分析可得到以下结论。

1）本文所提模型可获得合理有效的中长期合同电量分解方案及其梯级水库调度过程。分解结果满足合同执行约束，可确保合同电量的有效执行，保障市场主体利益，进而促进清洁能源消纳，为水电富集电力市场提供了一种行之有效的梯级水电站中长期合同电量分解方案。

2）该模型方法利用梯级水电站的调节能力，能够充分响应调度周期内的负荷变化、减小电网高峰负荷及峰谷差距、平滑剩余负荷过程，对于减缓余留日负荷波动程度的效果显著，进而有助于通过降低竞价空间的波动性而减缓水电富集电力现货市场电价的剧烈波动，利于市场的稳定运行。

3）不同目标的对比分析，验证了本文所提模型中公平性因素的敏感性，突显了市场化环境下合同分解过程中计及公平性带来的影响和意义，因此在合同分解过程中对于公平性的考量不可或缺。

此外，公平的量化不一而足，不同角度考虑的主要因素可能有所不同。本文只是提供一种面向现货市场条件下的以余留竞价空间调整程度为量度依据的解决思路。

4 结语

本文针对中长期市场与现货市场衔接的中长期物理执行合同的电量分解问题，建立了基于各流域梯级水电站间合同分解公平性，以余留现货竞价空间尽量均衡化为目标的中长期合同电量分解模型。该模型考虑了梯级水电站间复杂的水力和电力联系，以及合同电量的执行要求，并采用多项式拟合技术处理模型中多变量耦合非线性关系，将月尺度合同电量科学合理地分解至日尺度。以中国西南地区水电富集的云南电力市场为背景，采用澜沧江和金沙江流域梯级水电站进行多场景案例分析。结果表明，该模型能够合理地分解各流域中长期合同电量，并为现货市场提供均衡化的竞价空间，以期为水电富集电力市场提供一种行之有效的梯级水电站中长期合同电量分解方案。一方面可为市场运营机构分解提供决策支持，另一方面也可提供给市场主体作为其自行协商分解的参考。

中国电力市场改革正处于探索发展阶段，中长期市场有待进一步完善，现货市场仍处于试运行阶段。本文所提模型和算例，均存在一定程度的简化和理想假设，负荷预测误差、可再生能源出力随机性和波动性等不确定性因素将在后续研究中进一步考虑。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。