钢丝绳内外部断丝损伤识别

窦连城， 战卫侠， 白晓瑞

(1.青岛理工大学 机械与汽车工程学院， 山东 青岛 266520；2.青岛铭彧智能装备技术研究院， 山东 青岛 266000；3.海军工程大学 兵器工程学院， 湖北 武汉 430032)

0 引言

钢丝绳具有强度高、韧性好、自重轻等优良特性，常应用于煤炭开采运输中。由于工况条件复杂，钢丝绳在使用过程中容易出现各种损伤，导致其强度降低甚至断裂，危及工作人员生命及生产安全，所以定期对钢丝绳进行损伤检测至关重要[1-3]。钢丝绳最常见的损伤形式之一是断丝损伤，通常将一定长度内钢丝绳的断丝数量作为钢丝绳报废标准的首要指标[4-5]。钢丝绳断丝损伤可分为外部断丝与内部断丝。外部断丝产生于钢丝绳与其他零件之间的磨损，可用肉眼观测，但人工检测耗时长且极易疏漏[6]。内部断丝是由钢丝绳自身股间摩擦导致，不能被直接观测到。

随着机器学习理论的发展，神经网络模型逐渐被应用于钢丝绳断丝损伤检测中，通过提取漏磁信号的特征并将其输入神经网络模型中训练及分类，实现识别损伤。J. W. Kim等[7]采用一种基于霍尔阵列的多通道漏磁传感器采集漏磁信号，提取包络信号的多个特征，实现了基于人工神经网络的多阶段模式识别方法，用于检测不同断口长度及深度的外部断丝损伤。Zhang Juwei等[8]采用18个高精度巨磁电阻传感器组成传感器阵列以采集钢丝绳表面剩磁，并提出一种基于小波分解的自适应滤波算法，采用数字图像处理方法提取缺陷图像的多个特征，利用Elman神经网络对外部断丝类型进行定量识别。Huang Xinyuan等[9]采集钢丝绳损伤位置的光学图像，并采用卷积神经网络对缺陷图像进行分类，实现了不同断口深度的检测识别。钟小勇等[10]采用改进粒子群算法优化的BP神经网络对漏磁信号进行识别，检测外部断丝损伤。目前对于钢丝绳断丝损伤检测以外部断丝损伤检测为主，对内部断丝损伤检测的研究较少且内外部断丝识别精度不高。

本文提出了一种钢丝绳内外部断丝损伤识别方法。首先采用钢丝绳损伤径向漏磁检测器采集漏磁信号，然后利用双密度双树复小波变换对漏磁信号进行降噪处理，之后提取信号的时频域特征，并通过基于类间距离和互信息的特征选择方法获得最优特征子集，最后将最优特征子集输入BP神经网络进行定量识别。

1 漏磁信号采集与双密度双树复小波降噪处理

基于漏磁法[11-12]设计的钢丝绳损伤径向漏磁检测器由霍尔阵列、衔铁、衬套、永磁铁、聚磁环、导向轮等组成，如图1所示。霍尔阵列由12个周向排布的霍尔元件组成，在霍尔阵列上方装有聚磁环，可减轻由于钢丝绳振动引起提离值变化导致的漏磁信号失真。

(a) 模型

选取直径24 mm、类型为6×37+IWS的钢丝绳，人工制作9种不同数量、类型的断丝损伤，如图2所示。

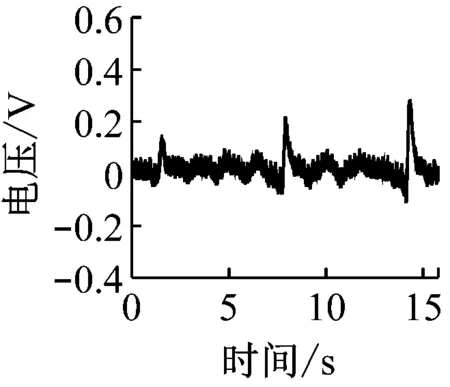
采用钢丝绳损伤径向漏磁检测器采集钢丝绳断丝损伤产生的漏磁信号，如图3所示(图3(a)中3个突变波形依次为内部1—3根断丝损伤产生的漏磁信号；图3(b)中6个突变波形依次为外部1—6根断丝损伤产生的漏磁信号)。可看出单根断丝损伤产生的漏磁信号较微弱，容易被噪声淹没；多根断丝损伤产生的漏磁信号较明显，但噪声的存在会给特征提取造成困难。

(a) 外部1根断丝

(a) 内部断丝

本文采用双密度双树复小波变换[13]对漏磁信号进行降噪处理。双密度双树复小波变换由2个并行工作的过采样迭代滤波器组构成(图4)，每个滤波器组由3个小波滤波器(h0—h2)组成且满足完美重构条件，具有高度的平移不变性。

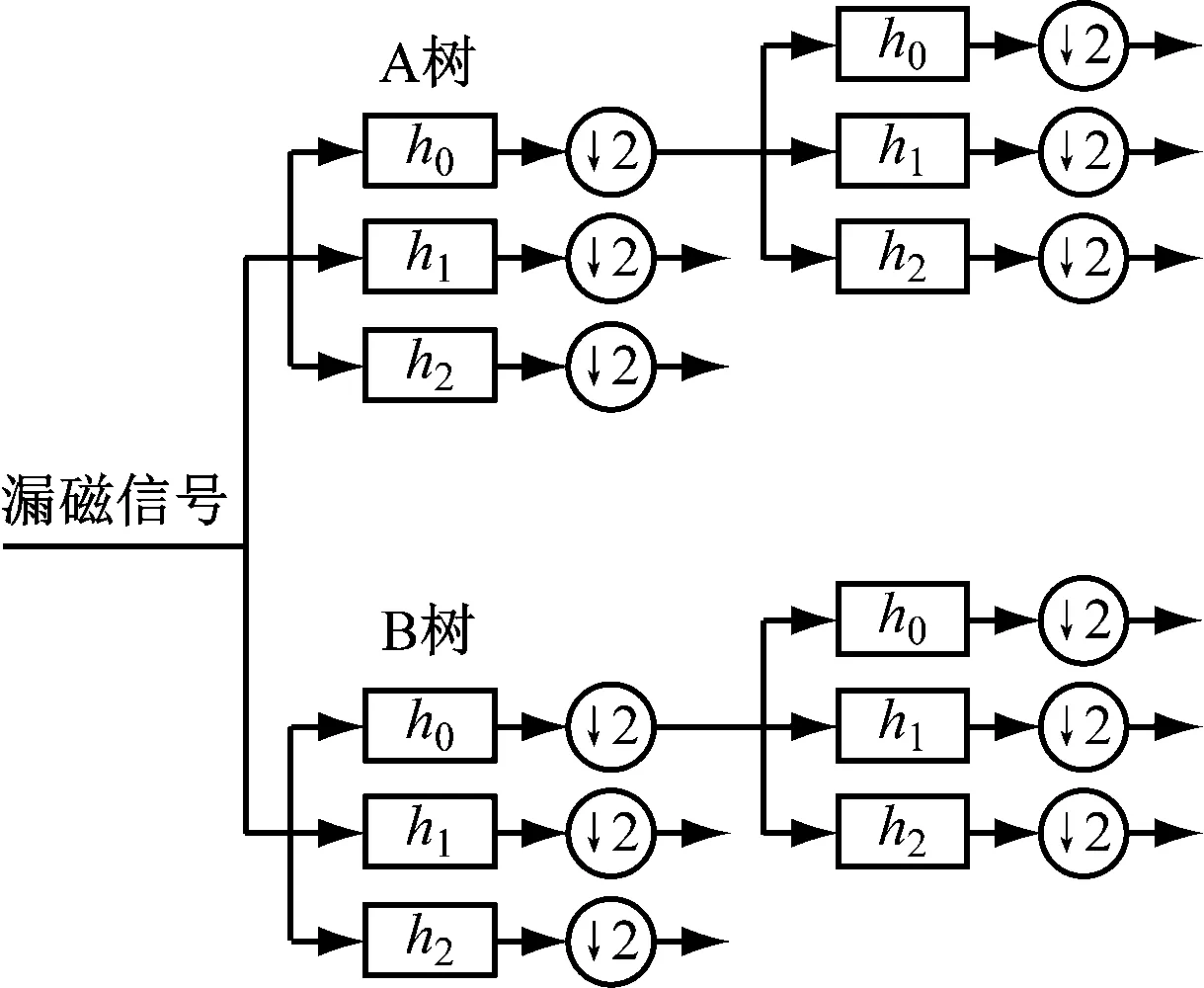
图4 双密度双树复小波变换的迭代滤波器组

对内部1—3根断丝损伤产生的漏磁信号进行3尺度下的双密度双树复小波降噪，然后采用最小二乘法消除由非漏磁信号产生的趋势项，得到降噪信号，如图5所示。可看出能够有效去除原始漏磁信号的噪声成分且保留漏磁信号的波形特征，得到的降噪信号整体平稳，降噪效果显著。

图5 漏磁信号降噪结果

2 漏磁信号特征提取及选择

2.1 特征提取

2.1.1 时域特征

漏磁信号的时域特征可反映钢丝绳断丝损伤的基本信息，需要设置特定阈值以达到不同损伤类型具有可区分性的目的，通常情况下阈值根据经验采用固定值，但是由于信号并不一定是一次性获取的，每次获得的信号会存在差异，所以需要阈值具有自适应性。根据数据的正态分布特性，选取平均值与标准差之和作为阈值，可有效排除离群值干扰。本文选取的自适应阈值为

(1)

式中：zi为第i(i=1，2，…，n，n为采样点数)个降噪后的漏磁信号采样值；τ为信号标准差；a为补偿数值，由经验获得，取0.015。

漏磁信号时域特征如图6所示。P为峰值；B为波形宽度；A为波形下面积；L为波形线长；D(x0，ymax)为峰值点；E(x1，y1)为波宽左端点；F(x2，y2)为波宽右端点。

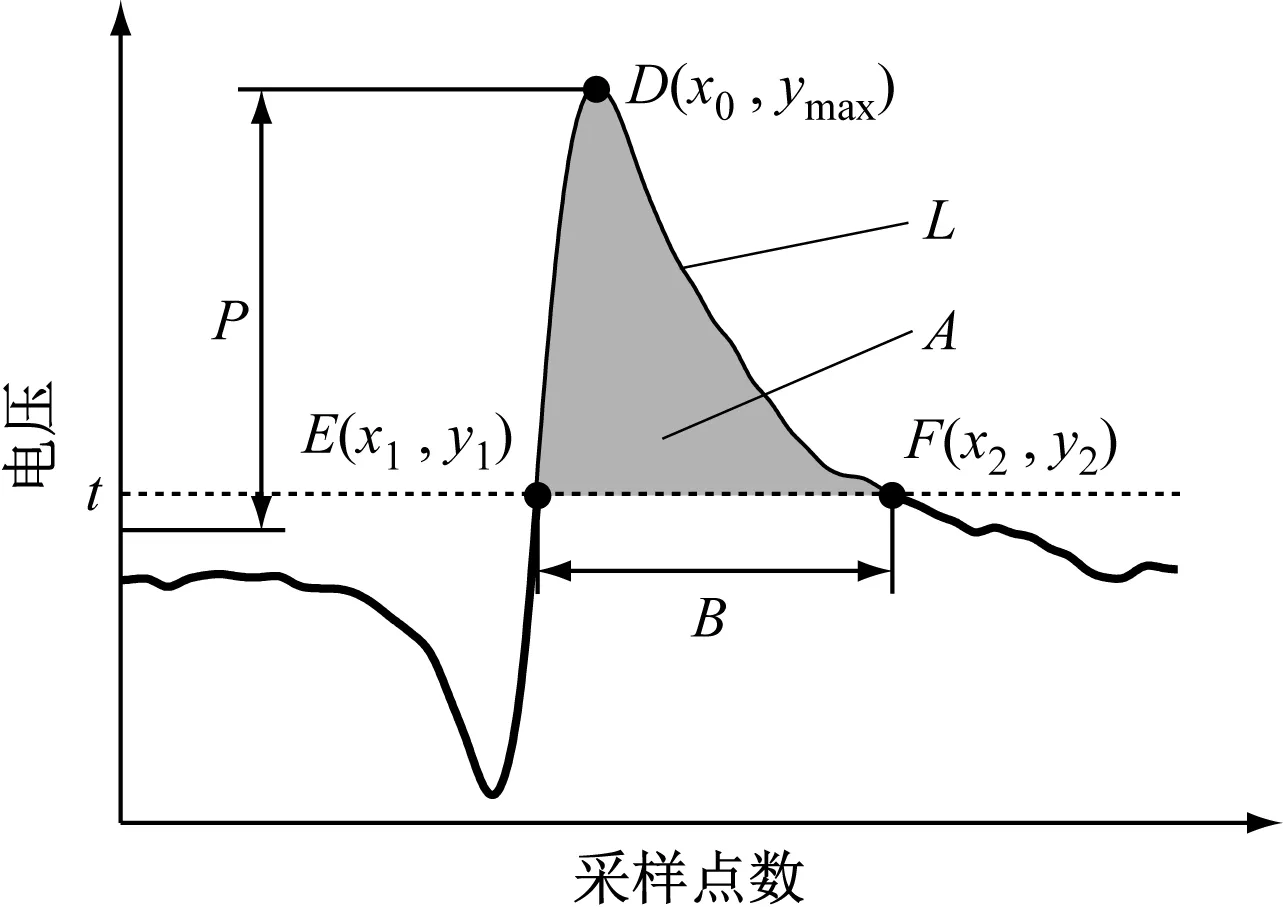
图6 漏磁信号时域特征

(1) 峰值。漏磁信号的峰值为

P=max[zi]

(2)

(2) 波形下面积。漏磁信号的波形下面积是指缺陷位置的突变波形与阈值间的面积，即

(3)

(3) 波形宽度。漏磁信号的波形宽度是指缺陷位置突变波形的跨度，即

B=x2-x1

(4)

(4) 波形线长。漏磁信号的波形线长是指缺陷位置突变波形的长度，即

(5)

式中T为采样周期。

2.1.2 频域特征

(1) 功率谱熵。对原始漏磁信号进行傅里叶变换得到Cj(j=1，2，…，n/2)，则功率谱密度为

(6)

式中ω为角频率。

将功率谱密度进行归一化，获得功率谱密度的概率密度分布函数：

(7)

则功率谱熵为

(8)

(2) 包络谱熵。先通过希尔伯特变换计算信号包络谱，然后计算包络谱的概率密度分布函数Ij，则包络谱熵为

(9)

(3) 奇异值。对信号进行10层变分模态分解，获得多个IMF(Intrinsic Mode Function，本征模态函数)分量，对IMF分量组成的矩阵进行奇异值分解得到奇异值σ1—σ10，奇异值是矩阵固有特征，可作为信号特征。

(4) 奇异值熵。计算奇异值的概率密度分布函数Wq(q=1，2，…，10)，则奇异值熵为

(10)

(5) 小波能量。对信号进行4层小波分解，获得4个细节分量dci(c=1，2，…，4)及1个近似分量oi，则第c个细节分量的小波能量EDc和近似分量的小波能量EO为

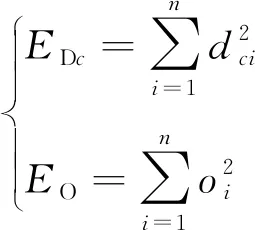
(11)

(6) 小波熵。计算小波能量的概率密度分布函数Kl(l=1，2，…，5)，则小波熵为

(12)

2.2 特征选择

时域、频域特征包含的信息不同，不同特征对损伤的区分度也不同，因此采用基于类间距离和互信息的方法进行特征选择，具体步骤如下。

(1) 对特征进行归一化处理。

(2) 计算每种特征的标准差，以标准差衡量特征的离散程度，剔除离散程度较大的特征。

(3) 计算每种特征的类间距离(式(13))，以衡量不同损伤类型的可区分性，剔除类间距离较小的特征。

(13)

(4) 计算特征之间的互信息(式(14))，如果2种特征之间的互信息较大，说明这2种特征包含的信息相似程度较大，剔除这2种特征中类间距离较小的特征。

(14)

式中：Q(U；V)为互信息，U，V为2种不同的特征；p(u，v)为U，V的联合分布；p(u)，p(v)分别为U，V的边缘分布。

(5) 根据类间距离判断区分度最差的2种损伤类型，从剔除的特征中收回这2种损伤类型类间距离最大的特征，以增加这2种损伤类型的可区分度。

经特征选择后，保留的特征为峰值P、波形下面积A、奇异值σ1和σ5、奇异值熵SW。将保留的特征融合作为最优特征子集并按损伤类型绘制散点图，如图7所示(内1—内3代表内部1—3根断丝损伤；外1—外6代表外部1—6根断丝损伤)。可看出峰值P、波形下面积A、奇异值σ1和奇异值熵SW特征可分离性较好，但对于内外部1—3根断丝损伤的区分不够明显；奇异值σ5特征可分离性较差，但能较好地区分内部与外部断丝损伤。

图7 最优特征子集散点图

3 基于BP神经网络的钢丝绳断丝损伤识别

对钢丝绳断丝损伤的识别过程实质上是建立不同损伤类型与信号特征的空间映射分类准则。BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络[14]，具有任意复杂的模式分类能力和优良的多维函数映射能力。BP神经网络结构包括输入层、隐藏层和输出层，其训练过程由信号的前向传播与误差的反向传播2个过程组成[15]。前向传播计算BP神经网络的损失函数，反向传播对BP神经网络的权重矩阵和偏置进行调整，多次训练后，使BP神经网络的期望输出与实际输出逐渐吻合。

将从钢丝绳断丝损伤漏磁信号中获得的最优特征子集按4∶1的比例划分为训练集和测试集。设置BP神经网络的隐藏层节点数量为13，隐藏层和输出层的激活函数分别为tansig和purelin，设迭代次数为300，学习率为0.1，目标为0.001。用训练集中的数据训练BP神经网络，当达到最大迭代次数或损失函数已达指定阈值时，BP神经网络训练结束。将测试集数据输入训练好的BP神经网络进行识别分类。

经过测试，BP神经网络的分类准确率为97.8%，测试集预测结果的混淆矩阵如图8所示。可看出仅在内部3根与外部3根断丝损伤类型中分别出现1次分类错误，对于其他损伤类型均分类正确。

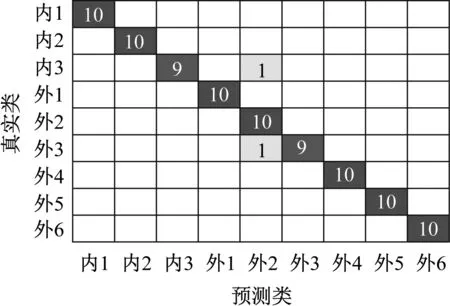
图8 预测结果的混淆矩阵

4 结语

为更加精确地识别钢丝绳断丝损伤的数量及位置，提出了一种钢丝绳内外部断丝损伤识别方法。首先对钢丝绳损伤径向漏磁检测器采集的漏磁信号进行基于双密度双树复小波变换的降噪处理；然后提取信号的时频域特征，并采用基于类间距离和互信息的方法进行特征选择，得到最优特征子集；最后将最优特征子集输入BP神经网络训练进行钢丝绳断丝损伤分类识别。该方法能识别钢丝绳内外部断丝损伤且识别准确率达97.8%。