煤矿井下超宽带定位混合解算方法

陈美蓉， 王凯， 张嘉纯， 许鹏远

(1.中国矿业大学 数学学院， 江苏 徐州 221116；2.煤炭科学研究总院 矿山大数据研究院， 北京 100013；3.中国矿业大学 信息与控制工程学院， 江苏 徐州 221116)

0 引言

随着移动终端的普及以及无人驾驶、智能机器人技术在煤矿中的推广应用，如何在井下狭闭空间内更准确地定位人-机-物，已成为制约智能矿山建设的瓶颈环节[1-2]。目前，常用的室内定位方法有红外线定位、超声波定位、蓝牙定位、射频识别定位、激光定位和超宽带定位等[3-4]，这些方法已广泛用于井下各类设备及人员定位。其中，超宽带作为一种无线载波通信技术，采用窄脉冲信号实现信号数据传输和无线通信，具有较高的数据传输速率、可共享的频谱、较低的拦截和检测概率及较强的抗干扰能力[5-6]，正在取代蓝牙、射频识别等定位技术，越来越多地应用于矿井人员和设备定位[7-8]。

超宽带定位是根据基站测定的标记点距离，基于一组非线性定位方程组，通过泰勒(Taylor)级数展开算法[9-11]、Chan算法[12]或最小二乘(Least Square，LS)法[13]解算获得精确的设备位置。其中，Taylor级数展开算法的求解精度高，但是对初始值具有很强的依赖性，如果初始值选择不恰当，会导致算法不收敛，因此，在迭代之前，应估计出较为准确的移动站初始位置。为解决该问题，本文提出了结合头脑风暴优化(Brain Storm Optimization，BSO)[14-17]和Taylor级数展开算法的新型超宽带定位解算(BSO-Taylor混合解算)方法。通过具有较好全局搜索能力的BSO算法，寻优获得具有较小定位误差的最优定位点作为Taylor级数展开算法的解算初始值，从而提升定位精度。实验验证了所提方法的有效性。

1 TDOA定位方法

常用的超宽带定位方法包括到达时间定位方法、到达时间差(Time Different of Arrival，TDOA)定位方法、到达角度定位方法和信号强度定位方法及混合定位方法[18]。其中，TDOA定位方法不要求基站与移动站之间时钟一致，只需每个基站之间时钟同步就能得到所需值，且在对到达时间作差的过程中会减小部分误差，定位精度能相对提高。考虑到煤矿巷道狭长封闭空间中基站和标定点的同步难度，本文采用TDOA定位方法。

TDOA定位方法也称为双曲线测距方法，通过测量标定点发出的信号到达2个不同参考基站的时间差值，解算相应的测距模型，获得标定点位置。TDOA定位系统如图1所示，将参考基站BSi之间时钟连接到同一网络，确保其保持同步。

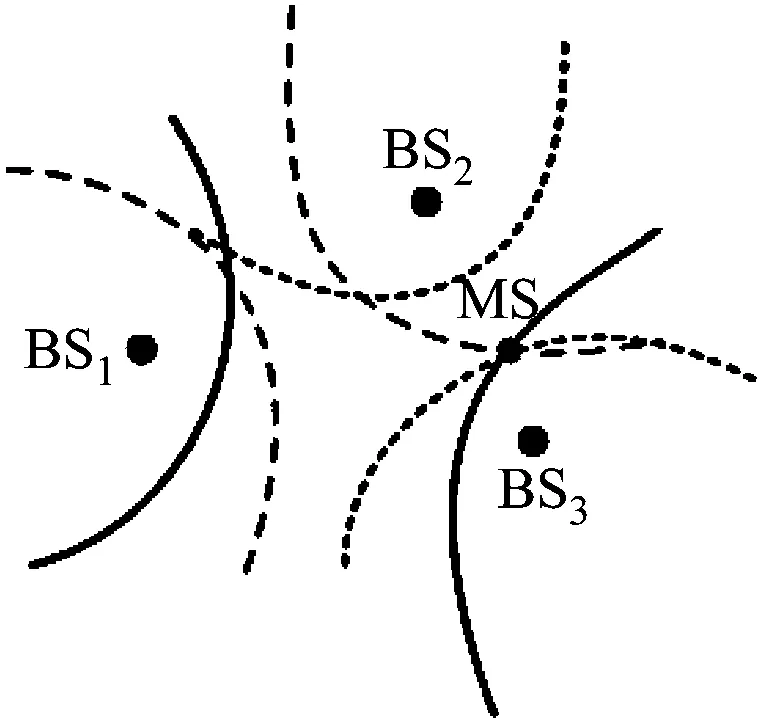
图1 TDOA定位系统

以3个参考基站BS1、BS2和BS3为例，设其坐标分别为(x1,y1),(x2,y2),(x3,y3)，移动站MS的位置坐标为(x,y)，其到达3个基站的距离之差分别记为D21,D32,D31，测距方程组定义为

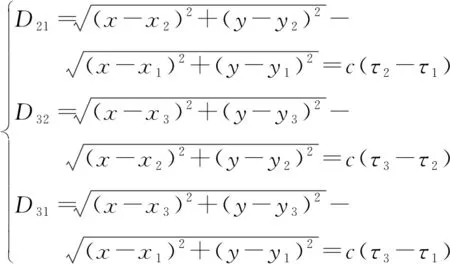
(1)

式中：c为电磁波传播速度;τi为第i个基站所接收信号的到达时间,i=1,2,3。

实际测量中存在噪声，式(1)不严格相等，因此，通过Taylor级数展开算法或Chan算法等非迭代方法求解式(1)，可以得到移动站的位置坐标。

2 BSO-Taylor混合解算方法

TDOA定位方法测定距离需要求解一组非线性定位方程组，目前主要采用LS法、直接法或Taylor级数展开算法进行方程求解。其中，Taylor级数展开算法是超宽带定位中重要的迭代算法。通过在每次迭代后求解TDOA测量误差值的局部LS解，以提高对移动站位置的估计精度。

2.1 Taylor级数展开算法

设待求解移动站MS的位置坐标为(x,y)，初始位置为(xR,yR)，测量误差为(Δx,Δy)，采用Taylor级数展开算法迭代计算，则移动站的解算位置与初始位置存在以下有关系：

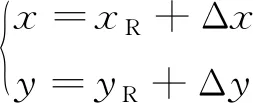
(2)

在初始位置坐标(xR,yR)处进行Taylor级数展开，并忽略二阶以上分量，可得

h=GΔ+ε

(3)

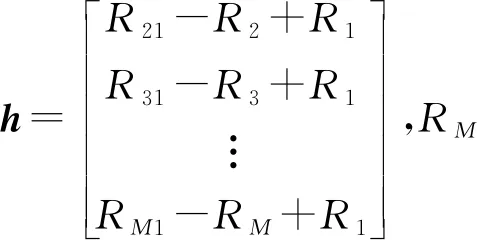
对式(3)进行加权LS法估计后得

Δ=(GTQ-1G)-1GTQ-1h

(4)

式中Q为TDOA测量值的协方差矩阵。

设误差门限为ε，下一次迭代计算位置坐标为x′=xR+Δx,y′=yR+Δy，重复以上过程，直到满足以下关系：

|Δx|+|Δy|<ε

(5)

2.2 BSO-Taylor混合解算方法

BSO由Shi Yuhui[19]于2011年首次提出，是一种模拟人类思考行为的新型群体智能优化算法。它将群体智能优化算法中的每个解视为一个数据点，通过对数据点的聚类进行分组，搜寻各组中的优势个体，找到问题的全局最优解。BSO已被用来解决多个领域的优化问题。

超宽带定位解算建模为单目标优化问题，以移动站位置坐标为进化个体，个体的取值范围取决于室内空间尺寸，其优化目标为最小化移动站到各个基站的误差函数之和。针对此优化问题，采用BSO算法求解适应度最小的最优解，并将最优个体的TDOA值作为Taylor级数展开算法解算的初始值，进行Taylor展开解算得到定位信息。

超宽带定位BSO-Taylor混合解算方法具体流程如下：

Step 1：以移动站位置坐标为进化个体，随机生成N个个体。

Step 2：在决策空间将个体进行聚类，分成K个集群。

Step 3：根据移动站到各个基站的误差评估个体适应度值。

Step 4：对每个簇中的个体进行排序，将每个簇中的最好个体作为该簇的中心。

Step 5：生成一个0～1的随机数，如果该随机数小于预设的概率P1，则随机生成一个个体，代替一个簇中心。

Step 6：生成新个体，过程如图2所示。

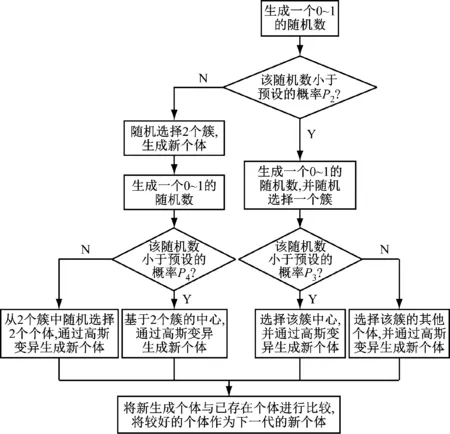
图2 生成新个体的过程

Step 7：如果达到了预设的最大迭代次数，则停止，否则转Step 2。

Step 8：采用以上进化算法得到移动站的最优位置坐标，作为Taylor级数迭代的初始值。

Step 9：将初始值代入式(4)进行迭代计算。

Step 10：若达到最大迭代次数或满足|Δx|+|Δy|<ε，则输出最优目标点；否则计算式(3)，并返回Step 9。

3 测距实验与解算方法性能对比

3.1 实验环境

考虑到井下巷道一般为狭长封闭空间，本实验环境为4 m×4 m×80 m的狭长巷道，基于P440模块实现超宽带测距，移动站的测量点位置如图3所示。4个基站的位置分别设为(0,0)、(100 m,0)、(0,100 m)、(100 m,100 m)，基于Matlab 2016b对所提方法性能进行对比分析。

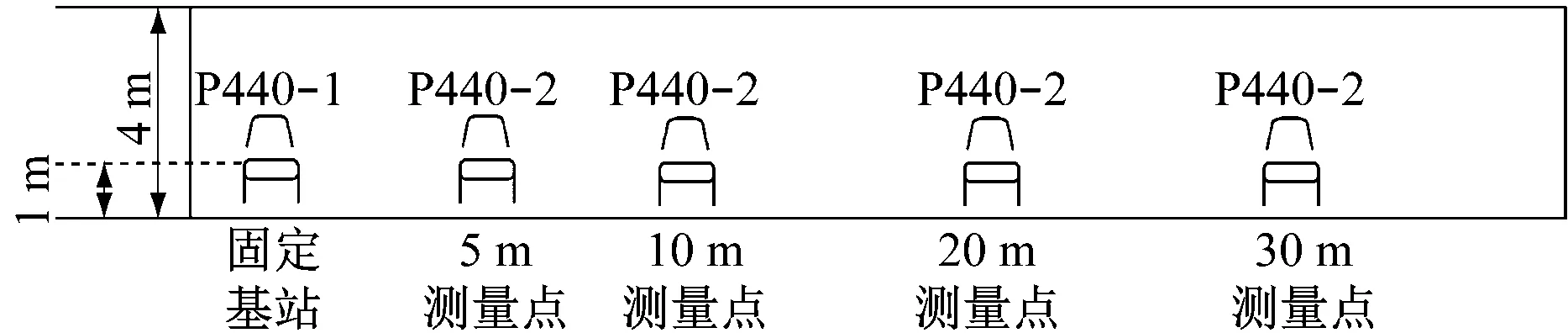
图3 移动站的测量点位置

被测移动站MS的实际位置选择为(50 m，50 m)，如图4所示。测量并采集目标移动站的测量值，分别应用Taylor级数展开算法、Chan算法[20]和BSO-Taylor混合解算方法求取移动站位置。

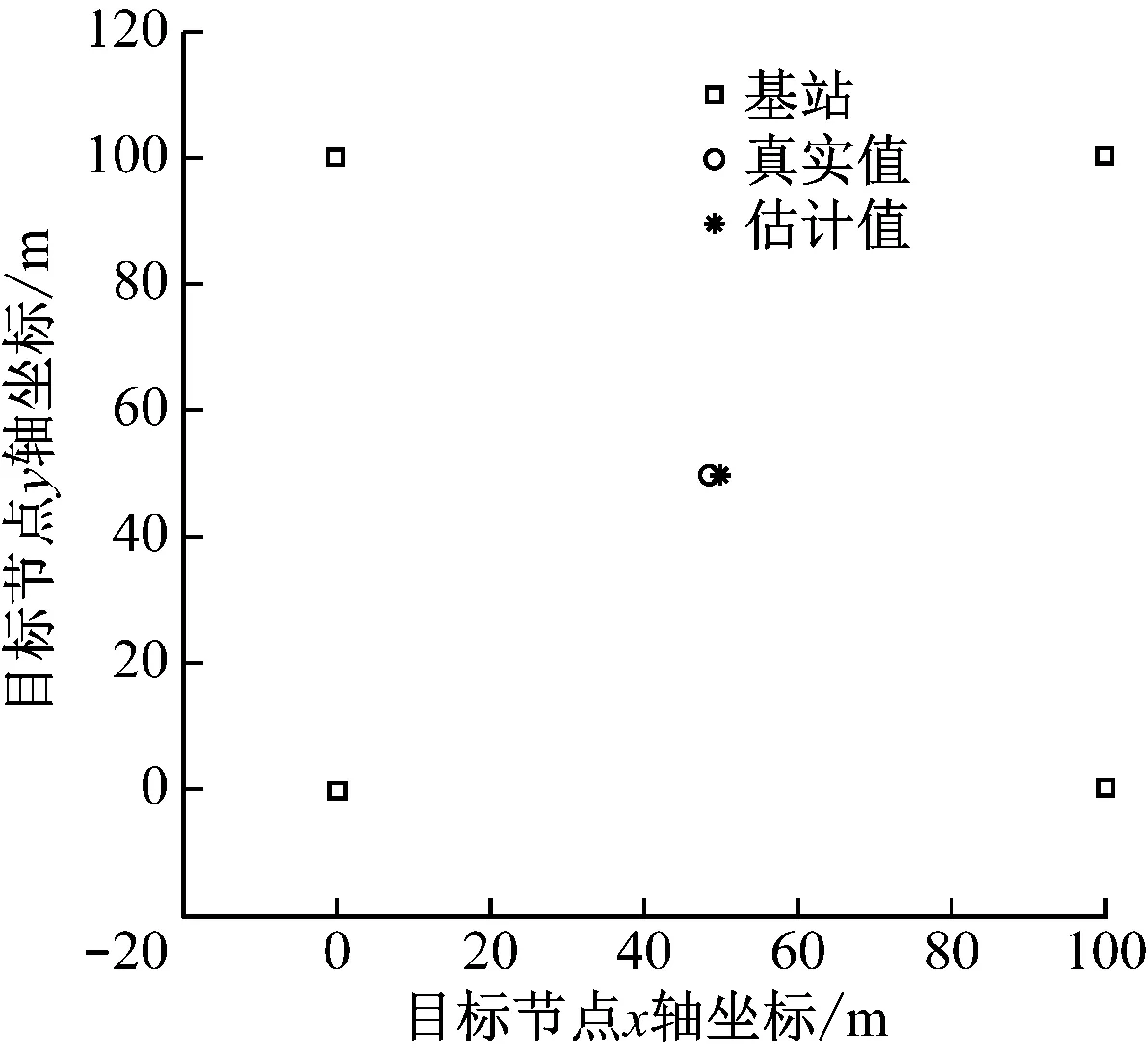
图4 被测移动站的实际位置

Chan算法是一种求解双曲线方程组的非递归算法，该算法采用两步最大似然估计，其特点是计算量小，在噪声服从高斯分布的环境下，定位精度高。

3.2 算法稳定性对比实验

Taylor级数展开算法是在初始值基础上，迭代寻找最佳移动站坐标。移动站的初始位置选择为真实值，如图5所示。算法运行10 000次位置解算得到的散点图如图6所示，解算的位置点大致沿着直线y=x两侧均匀分布，说明Taylor级数展开算法的稳定性较好。Taylor级数展开算法解算结果在x轴方向的误差如图7所示，从图7可看出，最大正误差不超过0.04 m，最大负误差不超过-0.045 m。Taylor级数展开算法解算结果在y轴方向的误差如图8所示，从图8可看出，最大正误差不超过0.08 m，最大负误差不超过-0.07 m。Taylor级数展开算法解算结果的均方根误差如图9所示，最大误差不超过0.035 m。通过以上分析可知，Taylor级数展开算法的定位解算结果较为稳定，定位误差较小。但实际上，Taylor级数展开算法对初始值具有较强的依赖性，上述较优的解算结果依赖于选取的迭代初始值是移动站位置真值。

对比分析Chan算法和BSO-Taylor混合解算方法的性能，运行10 000次位置解算得到的散点图如图10所示，相较于Chan算法BSO-Taylor混合解算方法的解算结果更加集中于实际位置附近，稳定性更好。

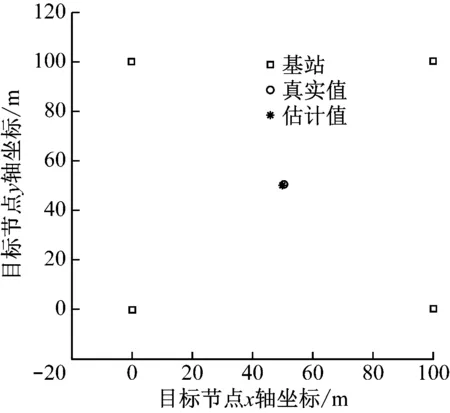
图5 Taylor级数展开算法移动站位置

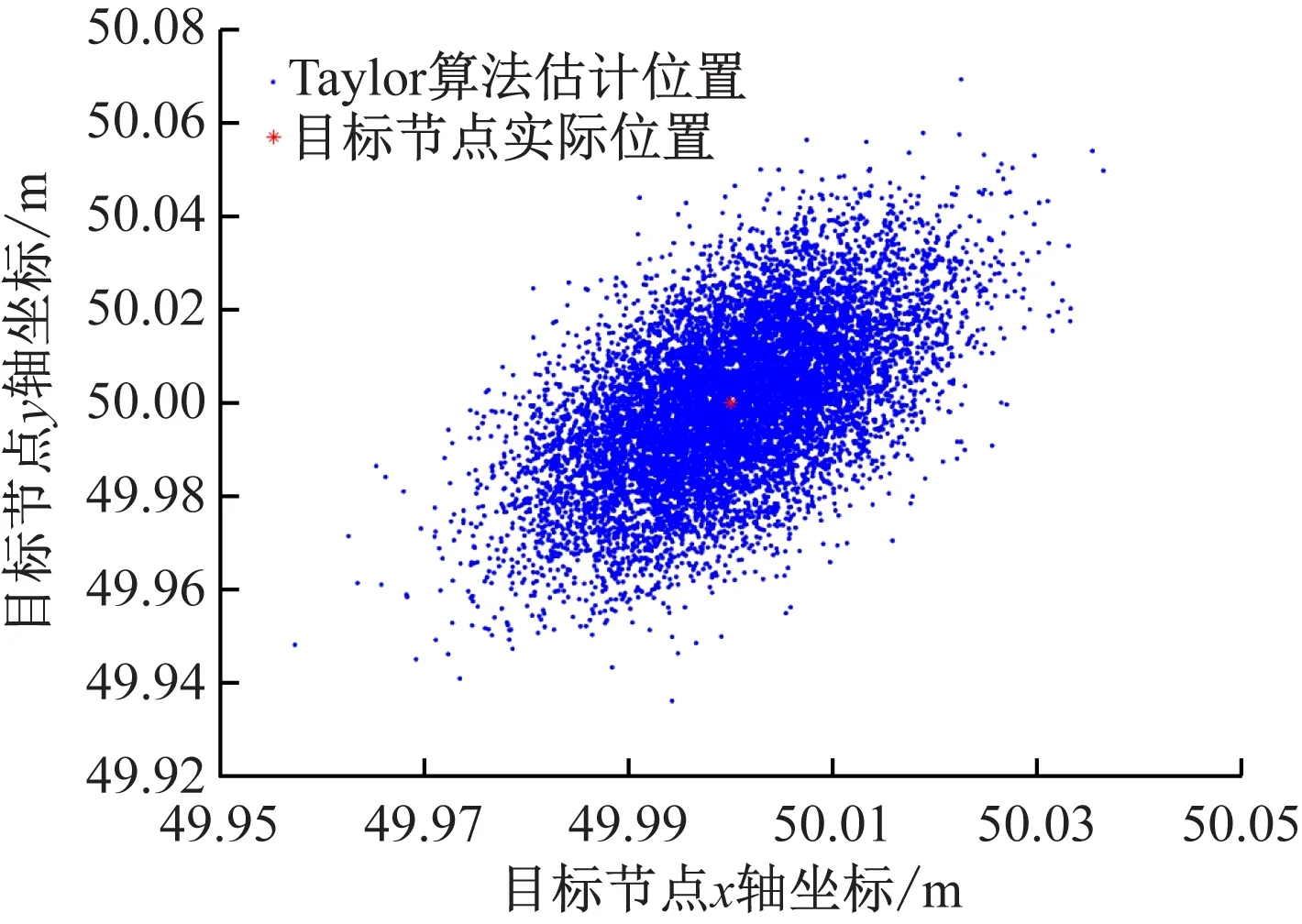
图6 Taylor级数展开算法散点图

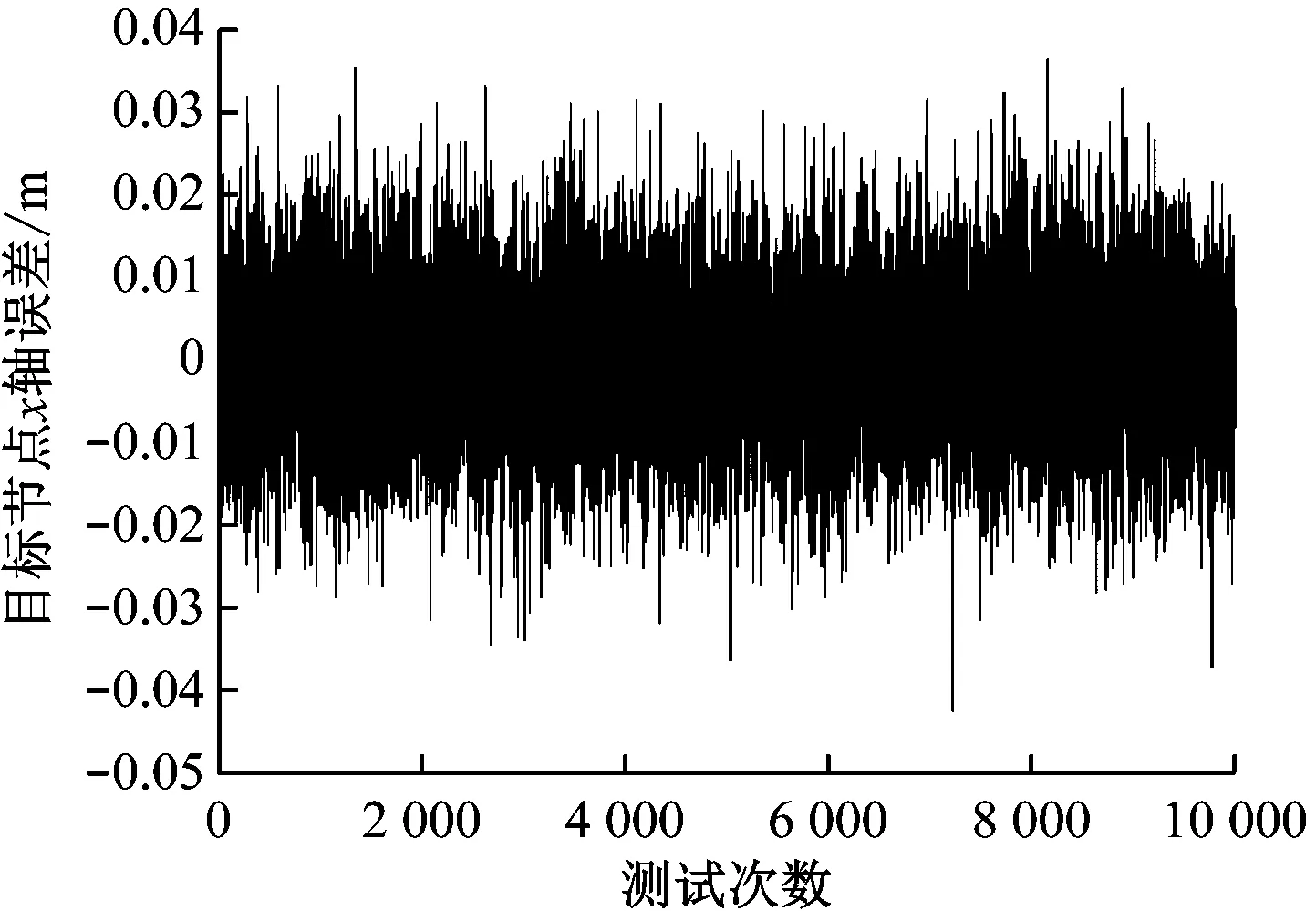
图7 Taylor级数展开算法x轴误差

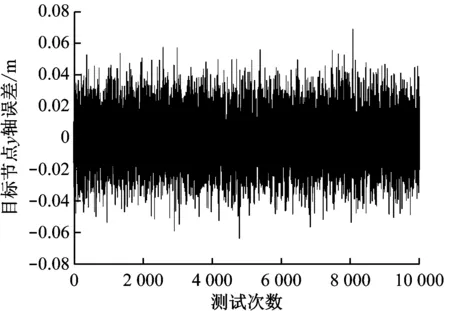
图8 Taylor级数展开算法y轴误差

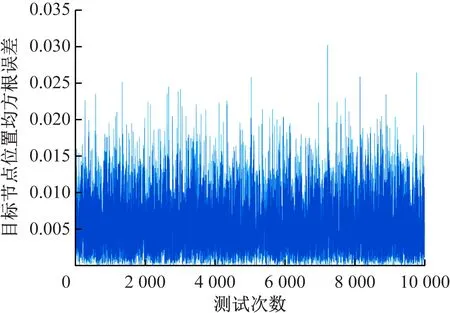
图9 Taylor级数展开算法均方根误差曲线

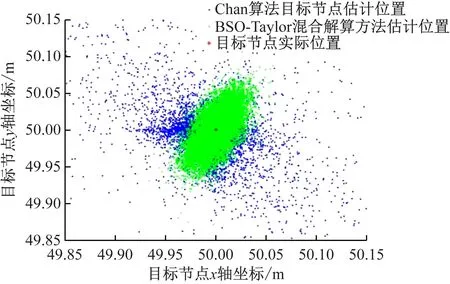
图10 Chan算法与BSO-Taylor混合解算方法散点对比

Chan算法与BSO-Taylor混合解算方法解算结果在x轴方向的误差对比如图11所示，Chan算法解算结果的最大正负误差分别不超过0.15，-0.15 m，而BSO-Taylor混合解算方法的解算结果的最大正负误差分别不超过0.10，-0.10 m。2种方法解算结果在y轴方向的误差对比如图12所示，Chan算法解算结果的最大正负误差分别不超过0.15，-0.15 m，而BSO-Taylor混合解算方法的解算结果的最大正负误差分别不超过0.10，-0.10 m。2种方法解算结果的均方根误差对比如图13所示，Chan算法解算结果的最大误差不超过0.12，而BSO-Taylor混合解算方法解算结果的最大误差不超过0.04。通过分析可以发现，BSO-Taylor混合解算方法相较于Chan算法的解算误差更小，稳定性也更好。

3.3 解算误差对比实验

将Chan算法、Taylor级数展开算法和BSO-Taylor混合解算方法的解算误差进行比较，5个标定点位置的解算分别运行100次的结果与真实值的标准差见表1。Chan算法的标准差明显大于另外2种方法，基于移动站真实位置的Taylor级数展开算法获得的结果具有略优于BSO-Taylor混合解算方法的性能，然而，实际系统中的移动站真实位置是不可能预先知道的。BSO-Taylor混合解算方法通过全局搜索策略，获得迭代初始值，性能接近Taylor级数展开算法。

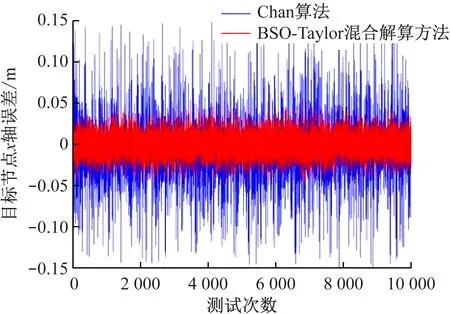
图11 Chan算法与BSO-Taylor混合解算方法x轴误差对比

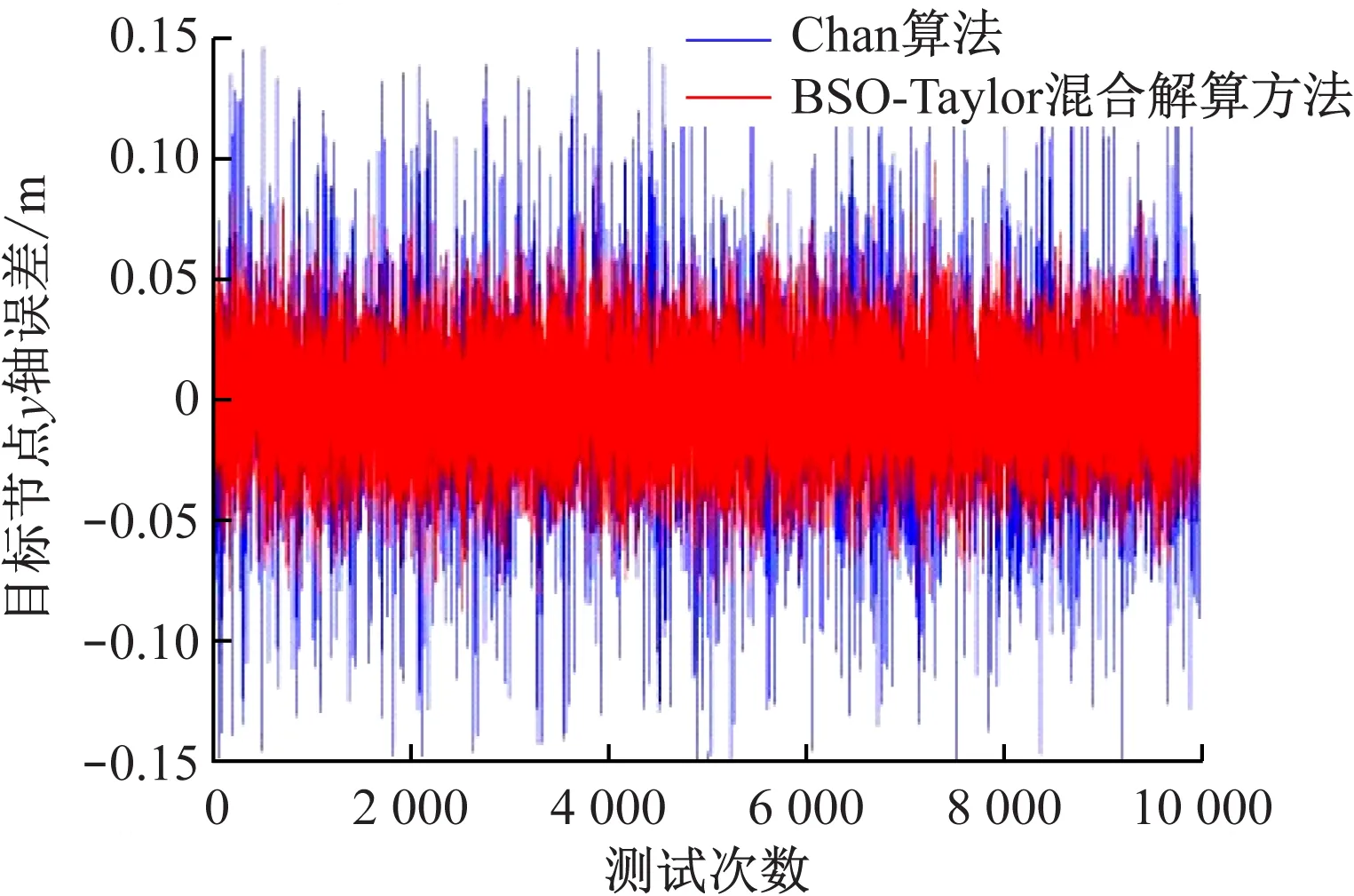
图12 Chan算法与BSO-Taylor混合解算方法y轴误差对比

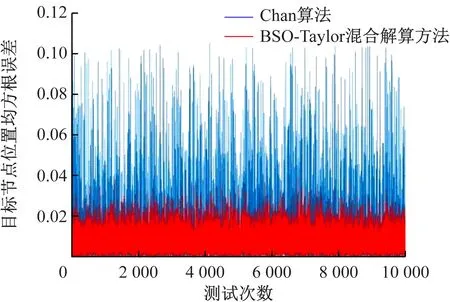
图13 Chan算法与BSO-Taylor混合解算方法均方根误差对比

为直观比较3种解算方法的定位精度，将移动站位置的y坐标固定为50 m，x坐标从0移动到100 m，移动站的位置解算结果如图14所示。通过比较3种解算方法的结果与真实值的误差可见，BSO-Taylor混合解算方法的解算结果误差稍大于基于真实移动站初始位置的Taylor级数展开算法，Chan算法的误差比前两者高。

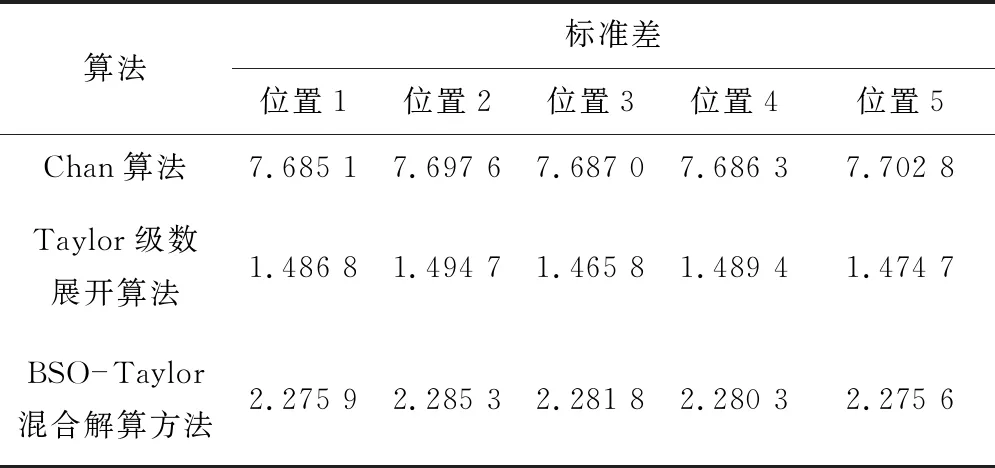
表1 3种算法解算结果与真实值的标准差对比

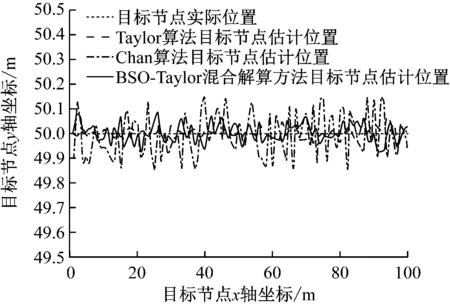
图14 3种算法解算的移动站位置结果与真实值曲线

在保持移动站标定点真实位置不变的基础上，移动参考基站，获得不同定位距离下的解算方法性能对比，如图15所示。显然，随着定位距离的增加，定位误差也逐渐增大。这是因为，随着定位距离的增加，多径传播误差和非视线传播误差也随之增加。尽管BSO-Taylor混合解算方法在60 m后的定位误差有所增加，但是仍大大低于Chan算法。

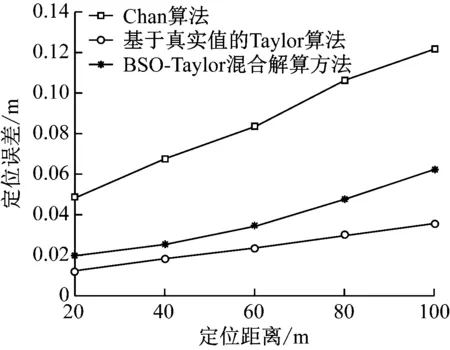
图15 定位距离对定位误差的影响

TDOA定位方法是将距离信号转换成时间信号的定位方法，因此, TDOA的测量值直接决定了上述3种算法的定位性能。选择不同的TDOA测量值标准差，对上述3种算法连续进行100次计算分析，取其均值作为最终仿真结果，如图16所示。可见，3种算法的定位误差随着TDOA测量值标准差的增加而增加。当标准偏差达到0.09时，基于标定点真实值的Taylor级数展开算法表现最佳，定位误差小于0.10 m。BSO-Taylor混合解算方法具有相似的定位误差变化趋势，定位精度明显高于Chan算法。

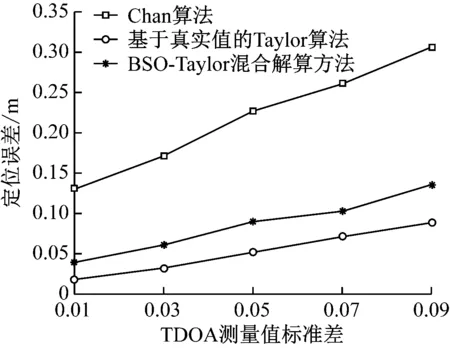
图16 TDOA测量值标准差对3种算法解算误差的影响

4 结论

(1) 提出了应用于煤矿井下超宽带定位的BSO-Taylor混合解算方法，基于BSO求取移动站到基站的误差函数最小化的最优解，并将最优个体的TDOA值作为Taylor级数展开算法的初始值，解决了Taylor级数展开算法需要较好初始值的问题。对Chan算法、Taylor级数展开算法和BSO-Taylor混合解算方法的结果进行了对比实验，结果表明，BSO-Taylor混合解算方法相较于Chan算法的解算结果更加稳定，且准确性更好；BSO-Taylor混合解算方法的误差稍大于基于真实标定点初始位置的Taylor级数展开算法，定位距离的变化和TDOA测量值标准差的变化对Taylor级数展开算法和BSO-Taylor混合解算方法的影响基本一致，而对Chan算法的影响较大。

(2) BSO-Taylor混合解算方法只适用于二维固定空间内以点为基站的超宽带定位解算，未来的研究应进一步解决三维定位以及非视距、多径传播、锚点分布和空间信号干扰等问题。