基于D-S 证据理论和区间粗糙数的直升机燃油系统重要度分析

刘洋

（中国直升机设计研究所，江西 景德镇 333001）

直升机燃油系统由燃油箱、燃油泵、管路等附件组成，主要用于储存直升机任务剖面所要求的燃油，并按要求向发动机等动力装置连续可靠地供油。燃油系统是直升机的重要系统之一，其可靠性对直升机飞行安全有较大的影响。目前直升机燃油系统的故障树分析大多认为底事件发生概率精确已知。实际中，由于系统的复杂性及故障样本量小，无法准确获得底事件发生概率，主要凭借专家和工程技术人员的主观经验，通用性差，对专家和技术人员依耐性强。因此，如何在小样本条件下准确进行重要度分析成为当前急需解决的重要问题。

本文以典型直升机燃油系统为研究对象，结合工程实际建立故障树，采用区间粗糙数和D-S 证据理论计算代表各底事件发生概率的综合发生度；在此基础上计算底事件概率重要度并采用区间排序方法对重要度进行排序，找到系统中重要度较高的底事件。

1 燃油系统故障树分析

故障树分析（FTA）是一种自上而下逐步细化的逻辑推理方法，常用于复杂系统安全性及可靠性工程领域。FTA 以不希望发生的故障事件为顶事件，结合系统原理、专家经验、外场维护数据，逐层分析直至找到最终原因事件。典型燃油系统组成如图1。燃油箱子系统用于储存任务剖面所规定量的燃油；供油子系统用于向动力装置供油；通气子系统用于保证压力平衡，满足通气要求。本文研究的燃油系统由两套典型燃油系统组成，每套系统单独向左发或右发供油或同时向双发供油。

图1 燃油系统

以 燃油系统无法为右发供油 为顶事件，建立故障树

图2 故障树

2 底事件重要度分析

重要度指系统中一个部件失效、最小割集或某一事件发生对顶事件发生概率的影响程度，包括概率重要度、关键重要度、结构重要度和相关割集重要度。本文目的是判断底事件发生概率的变化对顶事件的影响，故采用概率重要度函数作为判断指标。TP和PXi分别为T 和Xi的发生概率，为第m 个最小割集的发生概率，仅考虑前三阶最小割集，Xi的概率重要度为：

由式，重要度的计算结果主要依赖于底事件的发生概率。本文主要目的是进行重要度排序，故不需要精确的底事件发生概率，更加关注底事件发生概率的相对大小。由于故障特征的不精确性，无法获取部分故障数据的故障原因。针对这类数据，采用D-S 证据理论分析此类故障发生的所有可能原因，计算各底事件的频次信息，最终得到统计频率，为底事件的客观发生度。此外，由于样本量的限制，部分底事件无对应的故障数据。对这类底事件，基于参考事件和专家信息，利用区间粗糙数评估主观发生频率，为底事件的主观发生度。在此基础上融合主客观发生度，计算代表各底事件发生概率的综合发生频率，定义为综合发生度。

2.1 底事件客观发生度评估

D-S 证据理论能在较弱的条件下通过先验概率分派函数获得证据区间，定量表达命题的“不确定”。在D-S 证据理论框架下，命题B 的信任函数Bel(B) 、似真函数Pl(B) 分别如下：

Bel(B)和Pl(B)共同刻画命题的不确定性，其含义见图3。

图3 命题的不确定性区间

D-S 证据理论合成结果的可靠性很大程度取决于证据合成规则，为降低合成规则引入的悖论，本文采用[4]中基于全局冲突系数的组合规则。本文处理试验数据中故障原因不确定数据的方法如下：

（1）对某条故障原因不明确的故障数据，统筹专家列出的可能原因，形成识别框架

（2）总结专家判断的可能原因及组合iA，专家对各原因进行基本可信度赋值，M i(Aj)为专家i 对原因Aj的基本概率赋值。

（3）计算专家统一的基本可信度函数。

（5）为底事件累积频次加上相应的信任区间，得底事件Di的区间发生频次

（6）按步骤a-e 依次处理故障原因不明的故障数据，再进行归一化，得基于所有故障数据的底事件发生频率，即底事件的客观发生度，N 为样本量，为底事件Di的客观发生度，则：

2.2 底事件主观发生度评估

粗糙集理论利用下近似和上近似表征不确定问题的模糊性和随机性，具有较大的客观性，广泛运用于决策分析领域。本文利用多类专家信息处理外场未发生但实际可能发生的底事件发生概率评估问题，属决策分析范畴，故引入粗糙集。当粗糙变量的上下近似都为区间数时，则称该粗糙变量为区间粗糙数据，记为其中令则ξ1和ξ2的 距 离 为

为充分考虑决策者风险偏好，本文采用[6] 中方法，步骤为：

（2）考虑专家的风险偏好，计算各专家评分权重值wj。

（3）计算底事件区间粗糙评分效用值：

（4）定义ui的期望值为底事件Ei的主观发生度，并计算底事件iE的主观发生度：

2.3 底事件综合发生度评估

已知底事件的主观和客观发生度，需对二者进行融合，计算综合发生度。方法如下：

（1）对底事件进行客观发生度赋值，得底事件客观发生度集合：

（2）对底事件iE进行主观发生度赋值，对于不在集合E 中的底事件，其主观发生度赋0，得底事件主观发生度集合：

（3）融合各底事件的主/客观发生度：

考虑到融合后底事件发生度总和可能大于1，需进行归一化处理，定义为底事件的综合发生度。

3 底事件重要度排序

底事件的综合发生度iD gP为区间数，得到的重要度仍为区间数：

（1）选取可能度公式：

为区间数大于区间数的可能度。

（2）两两比较底事件重要度的区间数，计算底事件可能度矩阵

4 案例分析

依据试验数据和主观因素，对燃油系统无法为右发供油故障树底事件概率重要度进行排序。本文选出底事件发生频次见表1，未列出底事件频次为0。此外有7 条关于事件E6的故障信息未找到其原因底事件（数据已做处理）。

表1 故障原因频次

对不确定数据和没有对应故障数据的底事件进行处理。得出所有已发生底事件的区间数发生频次及归一化后的底事件 客观发生度 ，见表2。

表2 故障底事件发生度

考虑到专家规避风险，取τ=0.2 ，计算底事件的主观发生度，融合后的综合发生度见表2。各底事件的概率重要度结果见表3。由最小割集分析结果和式（1）知，TP与底事件X16 ～X20 无关，因此不计算底事件X16 ～X20 的概率重要度。

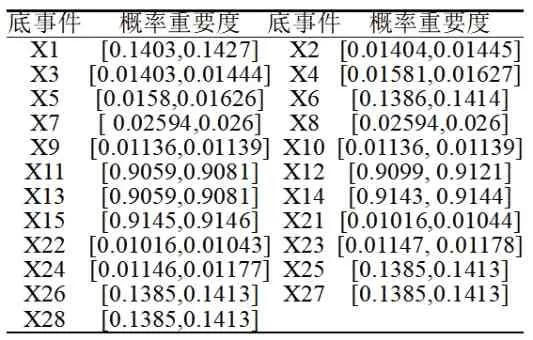
表3 底事件概率重要度

底事件重要度排序结果为：

由排序结果知，一阶最小割集中的底事件重要度大于高阶最小割集中的底事件重要度，与最小割集分析结果吻合；底事件X11～X15重要度排序结果靠前，需要重点关注；另外底事件X5、X21、X23、X28的发生频率较高，需要关注相对应产品的质量问题。为对比说明，分别以基于故障数据得到的底事件发生频率、底事件客观发生度均值、底事件综合发生度均值分别计算底事件重要度，结果见图4。三种计算方式下，底事件X11～X15的重要度都高居榜首，与最小割集求解结果一致；由于底事件X7 ～X10 与其他底事件无交联，故当X7～X10 的发生频率/客观发生度均值都为0 时，底事件重要度也为0。基于综合发生度计算得到的底事件重要度与利用其它数据得到的重要度值略有不同，但该方法考虑了多重因素，比完全利用故障数据的方法得到的结果更可靠。

图4 底事件重要度

5 结语

本文根据典型直升机燃油系统的组成及功能，以 燃油系统无法为右发供油 为顶事件，建立了故障树并找到最小割集，并以概率重要度作为指标开展底事件重要度分析。针对底事件发生概率难以获取的问题，计算用于代表各底事件发生概率的综合发生度。用综合发生度替代底事件发生概率计算各底事件的重要度，并对各底事件重要度进行了排序。结果表明：供油软管堵塞、供油软管泄露、自封阀意外关闭、供油选择阀故障、供油选择阀控制开关故障的重要度排序结果靠前。