结构力学中位移法的探讨

杨小钰

（山西工商学院，山西 太原 030062）

位移法是除力法外计算超静定结构的又一种基本的、有效的计算方法。在结构力学位移计算的两种方法中，一种是利用基本体系建立典型方程，它是以力法为基础，以独立结点位移为基本未知量的结构计算方法；一种是直接利用杆端力平衡条件建立位移法基本方程，这种方法同样是以结构独立结点位移相应的平衡条件建立位移法方程，以结点角位移为基本未知量建立结点力矩平衡方程，以结点线位移建立截面的投影平衡方程。位移法平衡方程和位移法典型方程既有相同点也有不同点，这二者本质上是相同的，前者便于理解和手算，后者便于与力法及以计算机计算为基础的矩阵位移法对比，从而加深对内容的理解。在学习时，要了解它们的共性，还要掌握它们的不同。这样才能有效地提高学习效率，更透彻地把握两种方法的计算步骤和基本原理。

1 位移法典型方程和平衡方程的探讨

在课本中，位移法是在力法之后学习。通过对力法的了解，学生对超静定结构的原理和解题方法有了初步的认识，即超静定结构的内力计算仅由平衡条件不能完全确定，还必须考虑变形协调条件建立补充方程才能求出。在已具备力法相关知识的基础上学习位移法基本原理时，可以通过与力法基本思路对比进行学习。

下面通过一个具体的示例说明位移法典型方程（如图1），该结构含有两个基本未知量：结点B 的转角Z1和结点C 的水平位移Z2。

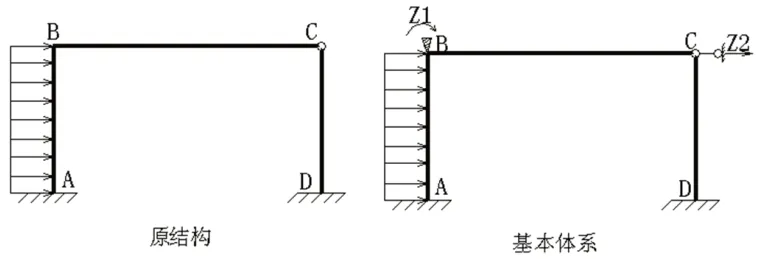
图1

位移法典型方程的基本体系如上图所示，该刚架的基本体系是在结构刚结点B 处加控制结点B 转动但不控制其移动的约束，称为附加刚臂，在结点C 处加水平支杆控制结点C的水平位移称为附加链杆。这就增加了与基本未知量相应的人为约束，由于增加了人工控制的约束，原来的整体结构被分割成许多单体杆件，从而结构由整体计算变为单个杆件的计算，简化了计算。为使基本体系的变形与原结构一致，则需使基本体系中的附加刚臂发生与原结构相同的转角，附加链杆发生与原结构相同的位移，对于此例，附加刚臂则需转动Z1，附加链杆水平移动Z2，此时，基本体系各杆的内力也和原结构完全相同，故附加刚臂上产生的反力矩R1和附加链杆上产生的反力R2均为零。即：R1=0、R2=0，由此即可以推出位移法典型方程：

建立位移法典型方程后，接下来求解方程时，首先使结点产生单位位移，由形常数得各杆受力，作弯矩图；其次，考虑外因作用，由载常数得各杆受力，作弯矩图Mp；最后，利用结点平衡条件求出各系数及自由项，解方程从而求出结点位移基本未知量，最终求得各杆件的内力。

我们同样以上面的例子分析位移法平衡方程，取结点B的角位移Bθ和结点C 的水平位移ΔBC为基本未知量，然后考虑变形协调条件并根据转角位移方程写出用基本未知量表示的各杆杆端弯矩和剪力表达式，在结点角位移B 处，建立结点的力矩平衡方程；在结点线位移C 处，建立截面的投影平衡方程，利用这些结点的平衡条件和结构中某一部分的平衡条件（通常为横梁部分的剪力平衡条件）建立方程组进而求得基本未知量，最终求得各杆杆端力。

2 通过实例计算对两种位移法进行比较

我们根据以上所说的计算方法，将图2 所示的实例采用不同的方法分别比较计算：

方法1：采用位移法典型方程

基本未知量Z1，Z2，Z3。

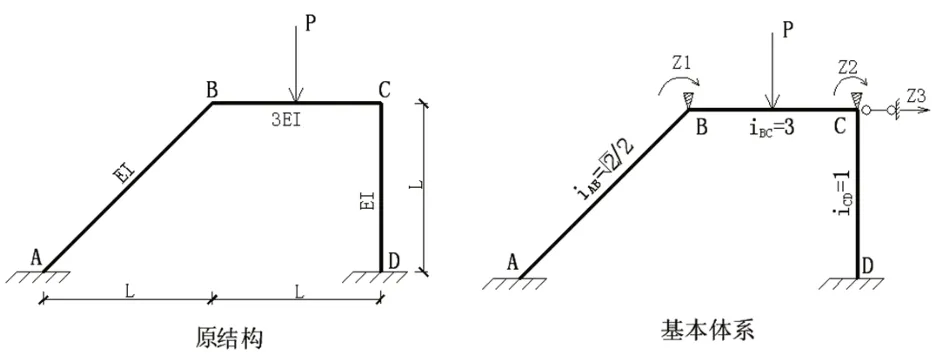
图2

位移法方程

求系数及自由项

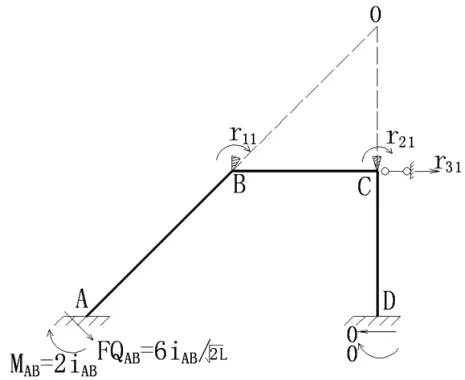
图3图

方法2：采用位移法平衡方程

（1）基本未知量θ1，，Δ。

（2）杆端弯矩。

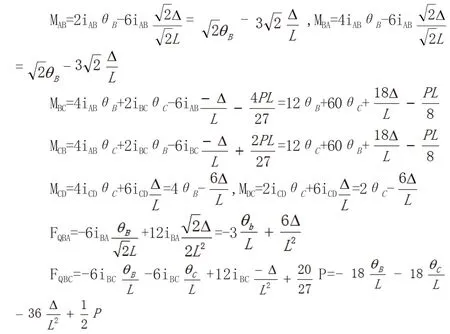
（3）位移法方程。

由结点B 平衡∑MB=0 得

结点C 平衡∑MC=0 得

取图4 所示部分隔离体，建立Y 向投影平衡方程，其中含有未知轴力FNBC，将B 点杆端剪力沿两杆轴向分解如图5所示，由∑FY=0 得

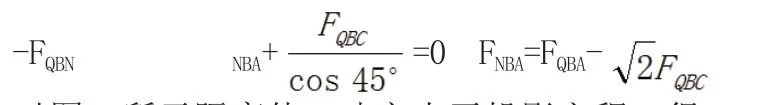
对图2 所示隔离体，建立水平投影方程，得

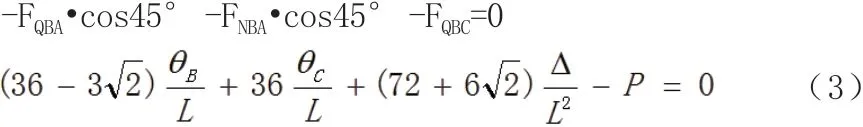
由（1）、（2）、（3）联立求出基本未知量，然后，将其代入各杆杆端弯矩中求得各杆内力。

图4

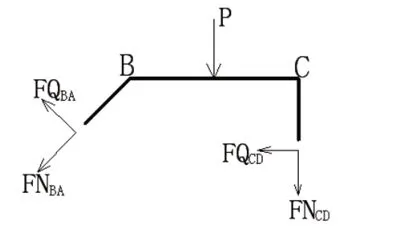
图5

3 结语

从上面分析可以看出，两种方法基本未知量的选取相同，且最终方程都是平衡方程，整理后形式均为。

不同点主要有两方面：首先，位移法典型方程是先利用平衡条件分别讨论各未知量和荷载的影响（即刚度系数和自由项），再进行叠加以得到典型方程，和力法一样，是在基本体系和原结构完全相同的基础上建立的，是一个和建立力法典型方程相对应的过程，所以直接对结构按统一格式处理，最终结果由叠加得到。而位移法平衡方程是先用叠加原理列出基本未知量的杆端力表达式，再利用平衡条件得到基本方程。其次，位移法平衡方程适用于全部由水平、竖直杆系组成的结构，当结构为具有多个斜杆的复杂刚架时，各结点线位移之间的关系不易判断，而且隔离杆件列平衡方程时会有轴力出现，需要将斜杆的轴力与剪力往水平方向投影，增加了求解方程难度，所以，建立方程求解相对较麻烦且易出错，所以，此种结构一般用位移法典型方程来求解。