元模型在供水系统节点压力实时估算的应用分析

王有平

(云南省滇中引水工程建设管理局楚雄分局，云南 楚雄 675000)

配水网是由管道、水库和泵站组成的复杂系统[1]。供水系统受到不同类型消费者需求的影响。水务部门必须以适当的数量和质量满足消费者的用水需求，同时通过有效的运作降低供水成本[2]。

泵站运行所消耗的能源是供水系统主要的运行成本之一。为了节约能源和降低成本，可以通过使用数学模型来使运行计划合理化，并通过实时优化使供水系统的运行得到优化。基于群体的算法，如遗传算法，已被用来优化水泵的调度方案，从而能够达到全局最优[3- 5]。然而，基于群体的技术需要大量的函数计算，使得这些方法计算效率低，因此不适合实时操作。

本文通过结合需求预测、水力元模型和优化的几种方法，实现有效和高效的水泵实时调度。并对云南省某供水系统进行了测试，分析元模型在供水系统实时运行中的应用。

1 研究方法及内容

1.1 水泵实时调度框架

水泵实时调度框架如图1所示。从该图中可以看出，水泵实时调度是通过使用每小时运行的水泵调度系统生成的。实施水泵实时调度程序如下：

(1)从数据采集子系统接收最新数据，用于估计当前系统中的用水量。这些数据包括水箱水位、水泵和阀门状态以及进出系统的流量。

(2)利用过去和当前的用水量数据预测未来24h的需水量。

(3)通过使用在步骤(1)和(2)中获得的数据，更新所分析的水力模拟模型。

(4)运行优化模型确定优化的系统程序，即未来24h的最佳水泵调度计划。

(5)通过监控子系统，在下一个小时执行上一步中确定的最佳水泵调度计划。

(6)连续重复步骤(1)至(5)，直到达到最佳调度。

1.2 需水量预测模型

需水量预测模型包括选择模型、定义其最佳结构和输入变量，以及定义其评估标准。本研究选择应用开发的混合动态神经网络进行需水量预测，这是一个自构造的神经网络，用傅立叶级数产生的预测需求对以前的用水量进行建模[6]。

需水量预测模型在每个时间步长(1h)提前24h进行估计，其值用于执行未来24h的供水网络运行。表1给出了模型的输入和输出内容。字符“C”表示消耗量，FS对应于傅立叶级数预测的需水量。预测模型使用前4h的数据加上滞后168h的数据。该模型以递归方式运行24次，以获得未来24h的需水量。

表1 混合动态神经网络模型及其各自的输入和输出

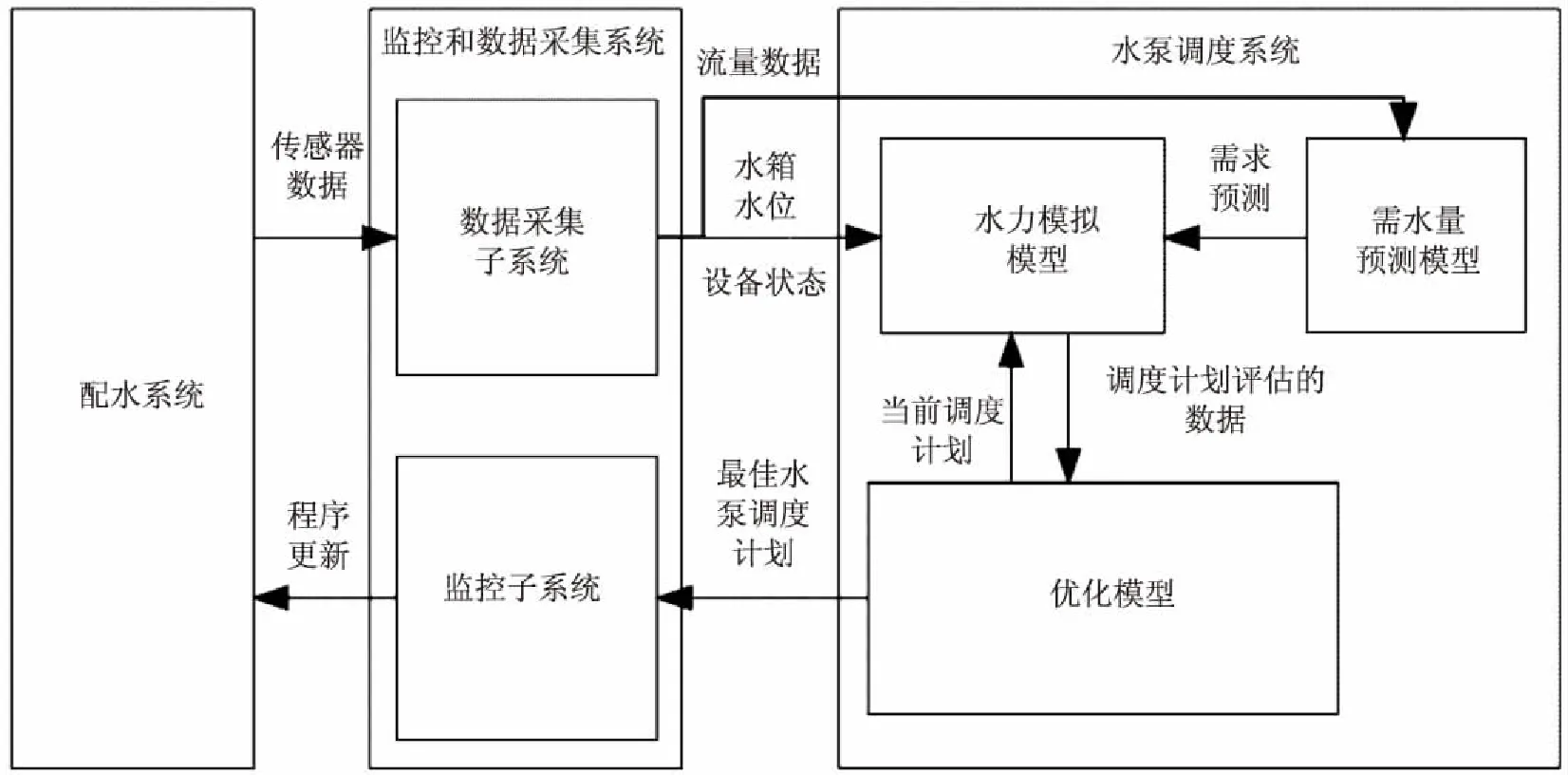
图1 水泵实时调度框架

1.3 优化模型

给定同一时间段的预测需求，通过优化模型确定未来24h的最佳水泵调度计划。水泵调度问题被公式化并作为具有特定目标、约束和决策变量的优化问题来解决。

1.3.1优化问题

目标函数将水泵在24h调度范围内使用的能源成本降至最低。优化问题中考虑了以下约束：

(1)压力不允许低于预先指定的最小阈值。

(2)水箱最终水位(即在计划周期结束时)不得低于同一时间周期开始时相应的水位。

(3)水泵开关的数量必须低于预先指定的阈值。因为过多的水泵切换会导致其过度磨损，并导致维护成本增加。

(4)液压模拟过程中出现错误，由系统断开或出现负压引起。这些错误是不被允许的，对应的方案不被采纳。

1.3.2水力模拟模型

水力模拟模型是通过使用基于人工神经网络的元模型来执行的[7]。考虑到供水系统及其运行的复杂性，所建立的元模型使用“总需求”、“水泵(开启)的数量”和“初始水库(水箱)水位”作为输入。“总需求”由Nd个输入表示，每个区域计量区一个，“水泵开启”由Np个表示，每组水泵一个，“水箱初始水位”由Nt个输入表示，总计(Nd+ Np+ Nt)个输入，如图2所示。

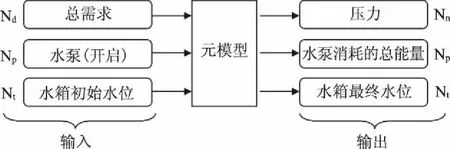
图2 基于人工神经网络的元模型

该元模型预测每组泵消耗的总能量Np、每个水箱的最终水位Nt和每个监控关键节点的压力Nn，合计输出为Nn+Np+Nt。

供水管网的水力状态(压力和流量)受管道系统物理性质和操作变化的影响，如管道直径、长度和粗糙度、水箱水位、节点需求、泵和阀门状态以及设定点[8]。根据网络拓扑结构的特点，并且考虑到粗糙度和需求的可变性以及它们周围的不确定性，通过修改这些参数，产生新的水力状态。

用于训练人工神经网络的数据库应该包含广泛的压力数据。因此，通过定义粗糙度和需求值的合理范围，可以为每个管道和节点生成真实的随机值。创建不同粗糙度和需求场景的优势在于，可以在没有预先校准的情况下使用水力模型，这在配水系统的计算分析中是一项艰巨的任务。

节点处的压力和入口流量，通过使用EPANET进行处理，目标数据库将一组受监控节点处的压力作为稳态的输入向量。在延长期内，除了节点压力之外，供应流量还用于人工神经网络的输入向量。相应的输出向量由所有其他节点的压力合成。重复该过程，直到数据库具有先前建立的大小。训练后，生成一个新的数据库来评估人工神经网络的适应性。训练数据生成的流程图如图3所示。训练结束后，预计人工神经网络可以仅使用从监控压力点收集的信息来再现所有节点中的压力响应，如图4所示。

图4 节点压力的元模型运行示意图

图3 人工神经网络训练流程图

1.3.3优化方法

选择多算法遗传自适应方法作为求解泵调度问题的优化方法[9]。优化仅限于2500个目标函数评估，总共有100个解决方案，这意味着使用了25次迭代。

系统操作的实时优化每天执行24次。每次生成未来24h的优化水泵时间计划。在实施第一个小时的计划之前，为了最小化高峰时间期间的水泵切换和使用，对下一个24h优化的水泵时间计划进行后处理。

元模型用于评估优化模型生成的水泵调度计划。然而，由于元模型是传统仿真模型的替代物，产生的目标函数也仅仅是近似的。因此，为了确保更好的解决方案，通过执行额外的500个目标函数评估，使这些解决方案再次得到优化。

2 案例研究分析

以云南省某供水系统为研究对象进行概化模拟分析。高峰时段和非高峰时段的电价不同，分别约为0.85、0.65元。高峰时间是指18:00至21:00之间的连续3h[10]。采用2010年4月27日—5月27日这一个月的数据做为区域计量区进行优化模拟计算。

概化后的区域计量区有18.5 km的管道，消耗54 m/h，对应的水力模型有252个节点，282条管道。供水设施由水库、泵站和两口井组成，如图5所示。水由井1和井2的水泵送到R8水库，由该水库直接供应分配。两台水泵都有144hp和115m3/h的供水量。R8的最低和最高水位分别为715.59、721.99m。元模型上监控的关键节点由图5中的红色箭头表示。

图5 供水系统布置图

元模型生成了5对输入、输出。校准使用了生成数据的75%，其余数据仅用于测试。在本案例研究中，使用了4个输入，因为有1个直接存储器存取Nd=1、两个泵组Np=2和1个水箱Nt=1。总计4个输出，即一个监控节Nn=1、两个泵组Np=2和一个水库Nt=1。

3 结果和讨论

3.1 元建模结果

表2中总结了元模型校准的结果，以预测水泵消耗的能量、水库最终水位和关键节点的压力。使用相关系数、平均绝对误差和平均百分比误差评估输出。从结果可以看出，所建立的元模型能够非常准确地预测输出。

表2 元模型的结果

3.2 水泵调度优化

该方法用了一个月的时间来比较优化后的成本和水务部门实际运行成本。在优化过程中使用元模型比使用传统的模拟模节省45%的处理时间。

如图6所示，比较了人工神经网络优化、全液压模型优化和水务部门实际运行的成本。针对所研究的直接内存分配确定的人工神经网络优化解决方案，在31d中有29d更加经济，而使用全液压模型有27d更加经济。在分析的时间段内，人工神经网络优化运行成本和全液压优化成本较水务部门实际的运行成本分别节约了约16%和14%。人工神经网络优化的方案在第9d比水务部门实际运行成本昂贵得多，而全液压优化在第2、3、9和11d更昂贵，因为优化的调度在高峰时间使用了更多的能量。在第30d，人工神经网络优化的水泵计划和水务部门操作之间的差异很小可以忽略不计。

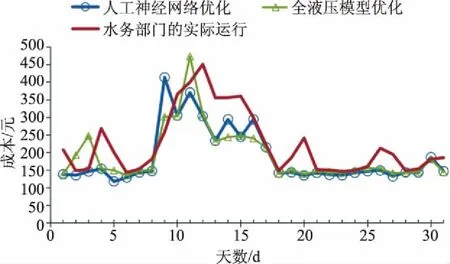
图6 优化操作和实际的成本对比图

4 结论

本文通过结合需求预测、水力元建模和优化等几种方法，实现有效和高效的水泵实时调度。对云南省某供水系统的计算结果表明：人工神经网络和全液压优化方法分别将泵调度成本与水务部门运行中使用的能源成本相比，分别降低了约16%、14%。除了降低成本之外，与使用传统模拟模型相比，计算处理时间减少45%。可知元模型优化方法和基于人工神经网络的液压元模型的耦合是用于水泵实时调度的有力且高效的工具，可供相关专业技术人员参考。

未来应该考虑成本以外的因素，例如可靠性度量，对本方法进行进一步测试，以提高其适用性。