基于线性观测器和状态反馈的多率输出采样控制

孙 娜

(山西工商学院 计算机信息工程学院，山西 太原 030006)

随着数字化测量技术与智能仪器的快速发展，采样控制系统[1～3]已经受到很大的重视。采样系统是一个混杂系统，它是由一个连续时间的被控对象和一个离散时间控制器组成。采样控制指对所需要的物理信号进行采样，得到的采样信息经过计算机进行处理进而产生控制。在状态反馈控制[4～6]中，最优控制、系统的镇定性都需要状态变量的有效信息，但在实际工业应用中，由于多率采样[7]方案的引入，使得控制器使用的量测信息在同一时刻可能不能全部获得，因而基于状态信息的状态反馈控制也难以实现。已有一些文献通过对状态变量的信息进行估计进而设计相应的控制器来保证系统稳定。文献[8～10]提出通过利用已有的输入、输出状态信息来重构一个动态系统(观测器)去预估系统状态的不可测信息，但这些观测器函数的构造在维数上都有不同要求。本文首先通过利用多率采样信息构造系统状态的线性函数，这样避免重建整个状态向量信息。其次，证明利用预定义函数进行状态反馈时闭环系统的稳定性。特别地，在这一部分，也提出所设计的预定义状态反馈控制器也适合于不可观测系统。最后，通过数值仿真案例证明所提方法的有效性。

1 问题描述与建模

考虑一个连续时间线性时不变系统，其状态空间方程表示如下：

其中，x(t)∈n，u(t)∈m和y(t)∈r分别为系统(1)的状态变量、控制输入和被控输出；A,B,C分别是维数为n×n,n×m,r×n的定常矩阵且(A,B)是可控的、(A,C)是可观测的。

本文假定系统(1)所有的状态变量即系统量测输出的采样周期为T.则上述的连续时间状态方程离散为下列离散时间LTI模型：

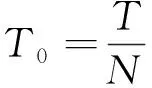
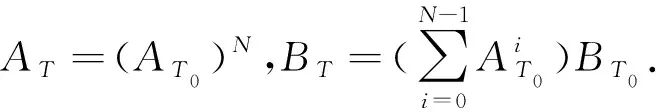
当输入向量以周期T进行采样，量测输出向量在t=lT0进行采样，系统表示如下：

(4)

其中l=0,1,2,…，N-1.当t=kT时，xk=x(kT),uk=u(kT),C0、D0以及输出向量yk+1定义如下：

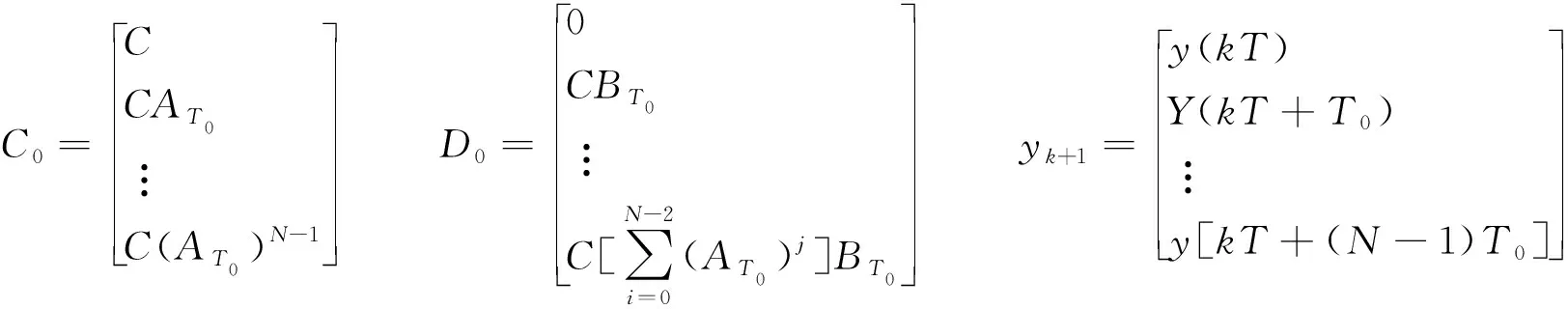
(5)

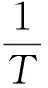
文献[10]中指出，当N≥υ时，可以定义如下的状态反馈控制器：

(6)

在本文中，可以证明N≥υ时不是一个必要条件。

考虑离散时间LTI模型：

其中(AT,BT)是可控的,(AT,C)是可观测的。

可以采取以下形式的控制器：

u(kT)=Fx(kT)

(7)

(7)中F是适当维数的常矩阵，通过利用多率采样信息来实现(7)的控制。

将xk+1=ATxk+BTuk代入(7)中得：

Fxk+1=F(ATxk+BTuk)=FATxk+FBTuk

等价的有：

Fxk=FATxk-1+FBTuk-1

(8)

由yk+1=C0xk+D0uk得：C0xk=yk+1-D0uk等价的有：

C0xk-1=yk-D0uk-1

(9)

如果FATxk-1和C0xk-1是已知的，通过yk和uk-1的信息可以得到Fxk.为了实现这个目的，应该求解FAT=PC0.

如果FAT=PC0有解，可以写成如下形式：

(10)

其中q是一个正整数且取决于所给定的线性函数。令μ是满足条件(10)的所有q的最小值，用μ表示可控性维数。由于有很多q是满足条件(10)，依据不同实际情况选取合适的q值。利用(8)和(9)，所需要的状态反馈函数Fxk可以定义如下：

Fxk=Pyk+(FBT-PD0)uk-1

(11)

具体推导如下：

将FAT=PC0代入(8)式得：Fxk=PC0xk-1+FBTuk-1，将C0xk-1=yk-D0uk-1代入

Fxk=PC0xk-1+FBTuk-1得：Fxk=P(yk-D0uk-1)+FBTuk-1，整理得：

Fxk=Pyk+(FBT-PD0)uk-1

P的值由FAT=PC0计算得出，输出向量yk由式子(5)得到，P和yk共同作为已知的输入序列。

2 闭环系统稳定性分析

在本节，我们对离散时间线性时不变系统进行稳定性分析。为了保证(11)式状态反馈函数Fxk的实现，Fxk=PC0应该有解。开环系统的输入信息由以下动力学系统得到：xk+1=ATxk+BTuk，进而，闭环动力学系统可以写成：

xk+1=(AT+BTF)xk

(12)

选取合适的F能够保证闭环系统的稳定性。

如果Fxk=PC0没有解即Fxk-PC0≠0，这表示状态反馈函数Fxk的实现中出现错误。这种错误会影响整个闭环系统。因此，闭环系统动力学模型可以如下表示：

其中Δuk=uk-Fxk

(14)

因此，当且仅当系统(13)状态矩阵的特征值在单位圆内，则闭环系统渐近稳定。

已有文献[8][10]说明为了预估系统状态所采用的线性函数方法仅适用于可观测系统。本文证明对于利用预定义状态反馈函数实现系统的控制中，系统的可观测不是一个必要条件。

考虑以下经过采样的一个不可观测系统：

即使q≤N时，(10)式也可以满足。当

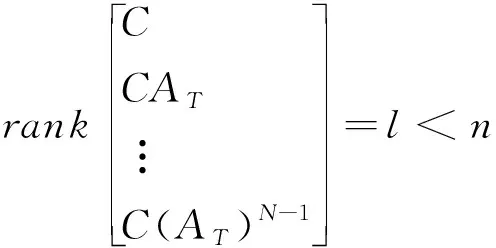
(16)

则系统(15)是不可观测的。

从(16)式中先选取l个线性无关行向量，此外再选取n-l个与之线性无关的行向量来构造矩阵Q，可得Q是非奇异矩阵。

根据(17)式和(18)式，l维可观测子系统动态方程可以表示为：

n-l维不可观测子系统动态方程表示为：

3 仿真结果

例1：考虑如下连续时间不镇定系统，该系统包含9个状态,1个输出和1个输入。

系统矩阵A,b,c表示如下：

其中：

该系统的特征根经过计算如下：

u(kT)=Fx(kT)

(25)

F=[F1F2]F1=[-9.34 -12.89 -19.28 -23.16 -31.88]

F2=[-5.16 -58.58 -19.15 24.16]

离散闭环系统的特征值如下：

该系统的采样周期为T=0.6s，T0=0.12s.利用本文所设计的状态反馈控制器(11)可以得到该仿真的最优控制器。其中，N=6,P的值给定如下：

P=103×[0.07 -0.41 0.92 -1.03 0.58 -0.13]

为了验证所设计的方案，取状态初始值为：

X0=[-2 -1 0 1.5 1 2.5 -1.5 3 -2.5]T.图1是N=6时预定义状态函数的值和它估计值的状态响应曲线。

时间(s) 时间(s)

当Fxk=PC0没有解时，系统在N=5时仍然可以达到稳定，这时系统(13)的所有特征值都落在单位圆内。图2显示了系统在N=5时真实值和近似估计值的状态响应曲线。

图3显示了随着采样时刻的变化，根据预定义状态反馈函数，得到的系统变量的误差响应曲线。

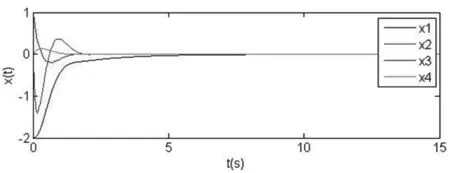
图3 采样时刻的误差响应曲线(当Fxk=PC0无解)

例2：用来证明所提出的控制器方案也适用于不可观测系统。

考虑如下连续时间系统，该系统包含8个状态,1个输出，1个输入。

系统矩阵A,b,c表示如下：

其中：

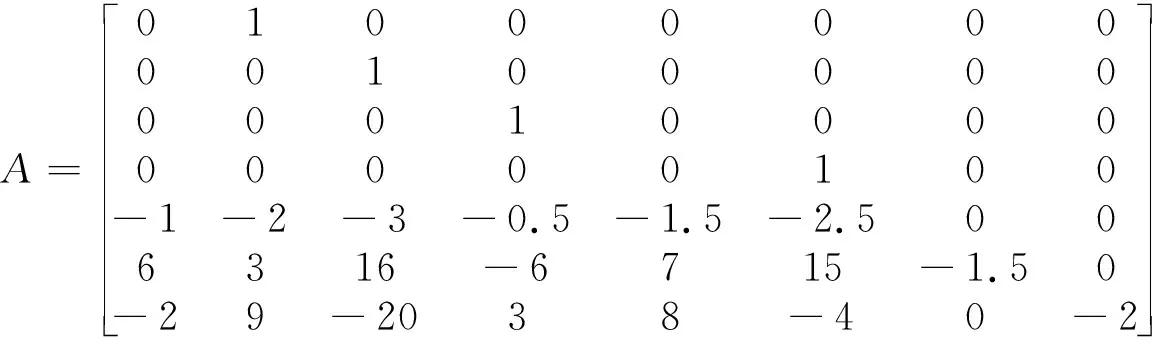
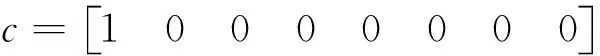
很容易看出，该系统有两个稳定的不可观测模式。利用本文第三部分对于不可观测系统所设计的控制方案，可以把系统分解为可观测和不可观测两种模式。利用第三部分的公式(17)和(18)，可以得到：

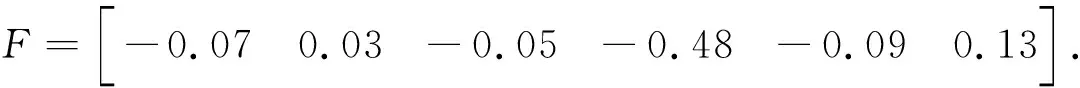
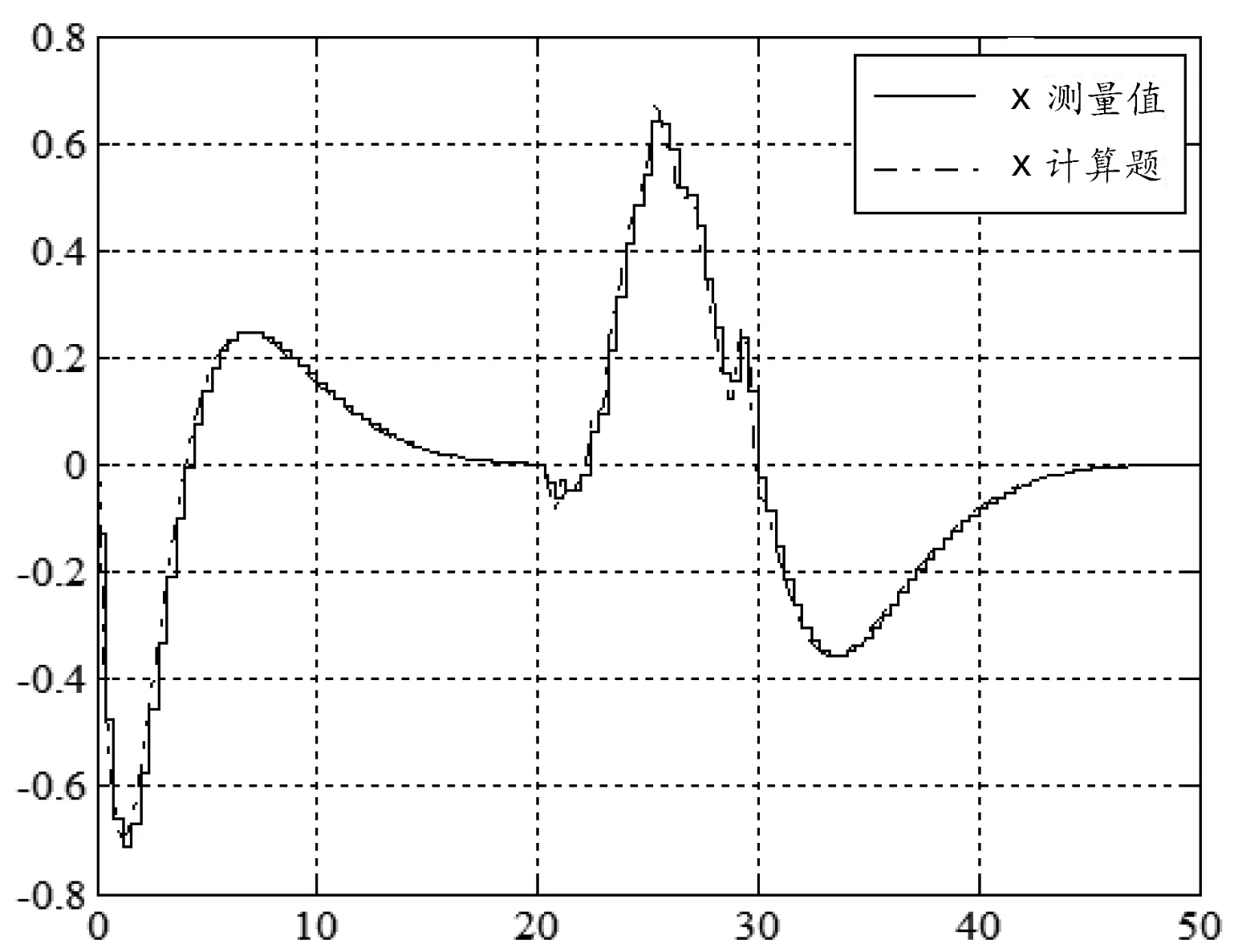
图4 近似预估计值与测量值的比较(N=5)

4 小结

本文提出了一种新的计算状态变量的方案——利用一个预定义线性函数设计状态反馈控制器。该方案可以推广应用到不可观测系统，所提方案最大的优势在于N≤ν时该方案仍然适用。对于一类不可观测系统，本文也证明了即使Fxk=PC0没有解系统仍然可以达到镇定。利用两个仿真案例证明了所提方案的有效性：在案例1中，对于一个含有9个状态变量的连续时不变系统，利用预定义状态反馈控制器，使得系统的预估计值和测量值基本没有差别；在案例2中，对于一个含有8个状态变量的不可观测系统，也证明了本文所设计的控制器方案仍然适用。