基于建构主义的“函数的概念”教学设计

江苏省南京市扬子第一中学 沈 艳

一、教学中发现的问题

将近7 年的教学工作中，我发现大多数学生在做题时往往会出现思维“短路”的现象：对某些概念、定理、法则和公式的记忆模棱两可，知识再现常处于“僵局”状态。对此，起初我认为是学生自身对新知掌握不够牢固的原因，后来慢慢随着教学经验的积累，我才发现，虽然数学课程改革已普及，但仍然存在“穿新鞋，走老路”的现象，在数学课堂中没有注重概念的形成过程，而是将概念作为“文字”教给学生，仅仅注重概念的应用，匆匆进行课堂练习，导致学生只是学习一些具体的解题技巧，缺少从感性到理性的认知过程，很难形成一定的数学能力。另外，忽视学生已有的知识经验，又没有给出一定的实例来揭露概念的关键特征，导致学生无法真正理解性地去学习并掌握概念，所以新概念不能较好地纳入学生的认知结构中，学生很难形成系统化的知识结构，这样学生的记忆不仅难以长期保存，而且不利于学生对知识的迁移应用，学生很难形成一定的逻辑思维能力。该现象存在的主要原因在于没有突出学生的主体地位，而建构主义突出强调：学生的学习活动要以学生为中心，强调学生的主动性，对知识的主动探究、对知识问题的主动发现和思考，进一步对知识意义的主动建构，所以有必要以建构主义理论为指导开展教学设计。

二、建构主义的内涵及其教学要点

建构主义是关于学习活动本质的认知论分析，其核心思想可以概括为学生在教师的指导下，依据已有的知识和经验，能动地建构数学认知结构。这一观点肯定了学生在学习活动中的主体地位，与传统的“填鸭式”观念直接对立，这就表明学生并非“空着脑袋”进课堂，同时也明确指出教师指导性工作的必要性和重要性，这就要求教师在教学中注重“学生的自主探究”与“教师的指导作用”的结合。此外，学习活动是学生积极主动参与的认知活动，它是在一定的学习环境下发生的，以学生原有的知识经验为基础，以实现知识的意义建构为目标。

因此，以建构主义理论为指导的数学教学应注意以下几点：

1.数学教学应注重创设适宜的“问题情境”

很多学生觉得数学枯燥无味且难懂，视数学学习为一种苦役，其根本原因在于学生缺乏对数学学习的兴趣。要使学生愿意主动地学习数学，成为学习的主体，如何激发他们学习数学的兴趣就显得尤为重要。建构主义认为学习环境有四大要素：“情境”“协作”“会话”以及“意义建构”，创设有效的“情境”，是激发学生学习数学愿望的一种很好的途径。良好情境的创设应注意以下几点：首先，不仅要注重导入过程的情境设置，在其他环节（探究新知、巩固新知、提高拓展等）同样可以通过创设情境促进学生的有效学习；其次，在激发兴趣的同时，更要注重情境的导向作用，对于相关内容的教学而言，适当的情境除了起到“敲门砖”的作用以及能够调动学生的积极性之外，还要能够在学习活动的进一步开展中自始至终地发挥一定的导向作用。此外，情境的选择要符合一定的学情，从学生的发展出发，创设特定情境，真正促进学习，这样才能较好地发挥“情境”的切实作用，保持学生的学习积极性，而不是为了情境而创设情境，要真正用好情境，使得学生始终处于良好的情绪中，能够积极主动地参与到整个课堂教学中，从而提高教学效率。

2.数学教学应实施“先行组织者”策略

作为数学教学过程中的主体者——学生，他们是完整的人，是处于发展过程中的人，在学习较陌生的新知识时，他们原来的认知结构中往往缺乏同化新知识的必要的上位观念，有时他们甚至概念不清。根据建构主义的核心思想，需要我们提供一定的引导性材料，从而激活学生已有的相关知识经验，建立新旧知识间的密切联系。这种引导性材料便是“先行组织者”，按照奥苏伯尔的“先行组织者”的思想，要求教师能够在学习材料呈现之前先呈现更一般的、有较大包容性的、清晰而稳定的引导性材料（组织者），而不是要求学生简单地机械记忆，从而构建一个使新旧知识发生联系的桥梁，促进学生的知识迁移，最终达到知识的意义建构。

3.数学教学应贯彻“会话”“协作”对学生数学建构起关键作用的思想

作为学习的主体——学生，他们的认知结构仍处于不断建立和完善的过程中，且他们的认知发展存在差异，不可能完全独立地学习，这就要求教师能够充分发挥自身作为学生发展的引导者和促进者（而不是强人所难的塑造者）的作用，能够创设适当的学习环境，引导并帮助学生逐步实现知识的意义建构。学习环境四大要素中，“会话” 与“协作”对知识意义的建构起着至关重要的作用，指出：学生在教师的组织和引导下一起讨论和交流，建立学习小组，在问题驱动下，通过对话交流与协作，使得每一个成员的思维成果被整个学习小组共享，共同完成对所学知识的意义建构。通过这样的协作环境，能够调动学生学习的主动性和积极性，充分发挥他们的主观创造性，从而利用学生自身的认知资源实现对意义的建构，进而实现“一切为每一个学生的发展”的教学目标。

4.数学教学应将“学生的自主探索”与“教师的指导作用”相结合

建构主义突出强调学生的主体地位，强调学生在学习活动中的自主探索，不过“自主探索”并不是让学生没有目的、毫无方向地瞎想，这样不仅没有意义，还有可能导致学生对科学探索严谨性的误解。

三、以建构主义理论为指导的“函数的概念”教学设计

【片段一】

师：同学们，如果你的爸爸打算开车带着你们全家去常州恐龙园游玩，你会关心哪些事情？

生：油量、天气、门票 、游玩项目……

师：上周末，老师就去了常州恐龙园，你们关心的事情也是老师关心的，首先，我去加油站加油，请同学们观察我在加油站拍的一段视频。

片段分析：从学生熟悉和感兴趣的问题情境导入，不仅可以调动学生的数学学习兴趣，而且整堂课都围绕该情境展开，所以该情境自始至终都发挥一定的导向作用。

【片段二】

观察加油过程中计费表的变化视频。

师：加油的过程中，涉及哪些量？

生：①油量；②金额；③单价。

（教师同时展示相关卡纸）

师：这3 个量出现的时候，分别有什么特点？

生：油量和金额在不断变化，而单价始终保持不变。

师：加完油，老师开车以100 km/h 的速度从南京匀速驶往常州恐龙园，在汽车行驶的过程中，涉及哪些量？

生：①速度；②行驶时间；③行驶路程；④剩余路程；⑤总路程。

（教师同时展示相关卡纸）

师：这5 个量各自又有怎样的特点？

生：行驶时间、行驶路程还有剩余路程在不断变化，而速度和总路程始终保持不变。

师：在刚才的两个变化过程中，我们得到了这8 个量，请你根据刚才分析的特点，将它们分为两类。

通过对CAM相关酶活性的测定证实，在盐胁迫下，随着光合作用的转变，一系列CAM必须酶的活性显著增强。McPpc1基因编码一个PEP羧化酶，该酶是 CAM 区别于 C3光合作用的关键酶［33，34］。 在盐胁迫下，McPpc1基因在叶片中的表达量明显增加， 而 PEP 羧化酶的活性增强了 40～50 倍［35，36］。NADP－苹果酸酶 （NADP－ME）、NADP－苹果酸脱氢酶（NADP－MDH）和丙酮酸磷酸二激酶（PPDK）也是CAM途径中CO2固定的关键酶，这3个酶同样也受盐胁迫的诱导表达。在受到盐胁迫时，这3个酶的cDNA 转录增强，酶活性也提高了 4～10 倍［37－39］。

生：单价、速度、总路程为一类，金额、油量、行驶时间、行驶路程、剩余路程为一类。

（教师同时调整卡纸位置）

师：你的分类标准是什么？

生：第一类的量保持不变，第二类的量不断发生变化。

师：根据它们的特征，能不能给它们起个名字？

生：常量与变量。

片段分析：在探究新知“常量与变量”环节同样通过创设情境，并在老师的追问下，不断激发学生已有的相关知识经验“变与不变”，从而建立新旧知识间的密切联系，促进学生的知识迁移，最终达到知识的意义建构——在老师的引导下，学生主动思考，在理解的基础上总结得到“常量与变量”的概念。

【片段三】

师：不知不觉，老师来到了常州恐龙园。请帮助老师解决门票问题。

常州恐龙园门票总额与游玩人数关系如下表：

人数x（人） 1 5 10 20 ……门票总额y（元） 210 1050 2100 4200 ……

师：在这个变化过程中，哪些量是变量？

生：人数和门票总额。

师：你能描述这两个变量之间的关系吗？

生：门票总额随着人数的变化而变化。

师：当人数确定时，门票总额有没有确定？比如，当人数取1 时，门票总额确定为210 元，此时门票总额有没有第二个值？再比如，当人数取20 时，门票总额确定为4200 元，此时门票总额有没有第二个值？……

师：补充说明门票总额与人数存在怎样的关系？

生：门票总额随着人数的变化而变化，当人数确定时，门票总额也随之确定，且有唯一的值与之对应。

师：也就是说，在这个变化的过程中，有两个变量：人数x 与门票总额y，门票总额y 不仅随着人数x 的变化而变化，更重要的是，当人数x 确定时，门票总额 y 也随之确定，且都有唯一的值与之对应。

片段分析：本节课始终围绕“恐龙园游玩过程中遇到的问题”这一情境展开，极大程度地激发学生的学习兴趣，在探索“唯一对应”环节，学生能够快速发现门票总额随着人数的变化而变化，但是很难发现门票总额随着人数的确定而唯一对应，此时就要充分发挥教师的主导作用，通过给予启发式的提问：“当人数确定时，门票总额有没有确定？”引导学生有目的地探索新知，进而达到逐一攻破难点的效果。

【片段四】

如图，四边形ABCD 是长方形，点P 是BC 边上的一个动点（不与点B、C 重合），连接AP。你能结合本题的背景提出问题吗？

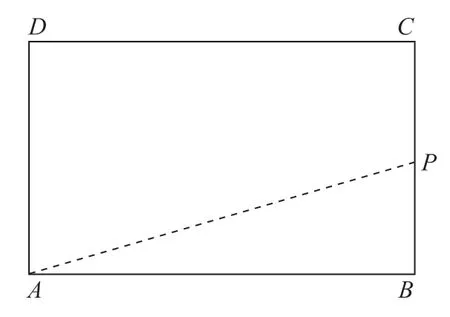
师：你能不能结合本节课所学内容，再结合本题的背景提出一些问题？小组谈论，小组长做记录。

片段分析：在新知巩固环节，为了加深学生对概念的深入理解，设置了一道“动点问题”，而且该问题是开放式的，引导学生从多角度思考。在一个变化的过程中，可能有多个变量，而函数研究的是其中两个变量之间的关系，也就是说，一个问题中可能存在多个函数关系。可见，本题有一定的难度，所以采取“会话与协作”的教学方式，在问题驱动下，通过对话交流与协作，使得每一个成员的思维成果被整个学习小组共享，共同完成对函数概念的意义建构。通过这样的协作环境，能够调动学生学习的主动性和积极性，充分发挥他们的主观创造性，进而实现“一切为每一个学生的发展”的教学目标。