多源场景下的无源雷达联合杂波对消技术

孙正豪, 吕晓德, 刘忠胜, 刘平羽

(1. 中国科学院空天信息创新研究院, 北京 100094;2. 微波成像技术国家重点实验室, 北京 100190;3. 中国科学院大学, 北京 100049)

0 引言

无源雷达利用FM广播、数字电视信号、通信信号等第三方非合作辐射源进行目标探测[1]。由于无源雷达本身并不发射信号，其具有无辐射、不占用频谱资源、反隐身、抗干扰、成本低等优点，近年来已成为国内外的研究热点[2]。

传统的无源雷达杂波对消方法[3-5]只针对一个信号源的直达波和多径杂波，当无源雷达回波信号存在多个信号源时，其性能受到较大影响。LTE信号作为外辐射源时，具有易于布站、分辨率高等优势[6-10]。但是由于LTE信号采用蜂窝式布站方式，各个发射基站信号的频段相同，无源雷达回波信号不可避免存在同频干扰杂波，文献[11-13]研究了基于盲源分离算法的同频干扰基站信号的分离，利用分离信号一一对消回波信号中的同频杂波，未涉及传统杂波对消算法用于多信号杂波对消所存在的滤波器权值收敛误差大和杂波对消比降低的问题。目前常用的是基于最小均方误差(LMS)算法的杂波对消算法，一一对消时，后对消信号的存在会影响先对消信号的滤波器权值的收敛，收敛误差大，使滤波器权值无法达到最优解，导致杂波对消比降低。为保证无源雷达的检测性能，必须提升多信号源杂波对消的性能，改善传统一一对消方法存在的不足。

针对传统无源雷达杂波对消方法逐个对消同频信号源的直达波和多径杂波的效果较差，本文分析了多个信号源对传统杂波对消方法产生的影响，并提出了一种基于联合处理模型的杂波对消算法。该方法在传统LMS算法的基础上，以多个同频基站信号为输入，同时对消所有信号的直达波和多径杂波，避免了一一对消所存在滤波器权值收敛误差大的问题[14-15]。另外，由于数据量大，对消阶数高，直接采用联合LMS对消算法所需的计算量大，无法满足实时性要求。因此提出了基于频域分块LMS的联合杂波对消算法(联合对消FBLMS)，通过频域分块的方式减少计算量，同时块内可以通过快速傅里叶变换(FFT)进行计算，大大降低计算复杂度。

1 同频干扰信号对LMS算法的影响

传统单信号源无源雷达的信号模型如式(1):

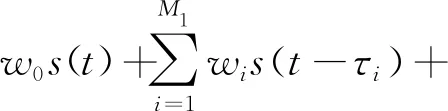
(1)

式中:s(t)为直达波信号，假设为零均值;wi,hi表示信号幅度;τi,ti分别表示多径时延和目标时延;M1，M2分别为多径数目和目标数目；fdi表示多普勒频率；n(t)表示噪声，噪声为零均值，且与信号之间相互独立。

基于LMS的无源雷达传统杂波对消方法原理如图1所示，其中e(t)为回波信号经过杂波对消后的输出信号，w(t)为滤波器权值，其阶数取决于最远多径时延所对应的离散点数。假设杂波对消的滤波器阶数为N，满足N-1≥max(τi)/T，令

(2)

(3)

式中，μ为步长因子。

图1 基于LMS的无源雷达传统杂波对消方法原理

当存在同频干扰杂波时，无源雷达的回波信号模型为

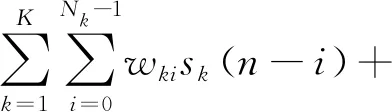
(4)

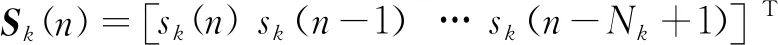
(5)

(6)

式中，K为发射基站数目，sk(n)为第k个发射基站的直达波信号，假设信号源都是零均值，且独立同分布，获取各个发射基站的直达波信号文献[11-13]已进行研究，不妨假设已获取所需的直达波信号，k=1时表示主基站信号；n(n)表示噪声，q(n)为目标回波和噪声之和。为方便运算，取N≥max(Nk),∀k，即令K个滤波器的阶数都为N。

(7)

式中，

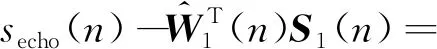
(8)

将式(8)代入式(7)得

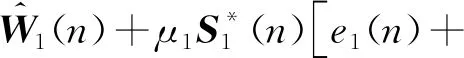
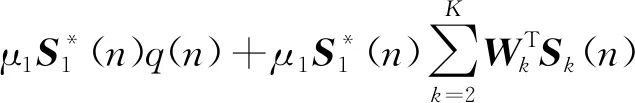
(9)

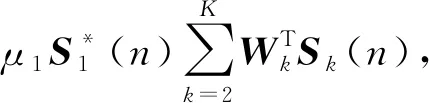
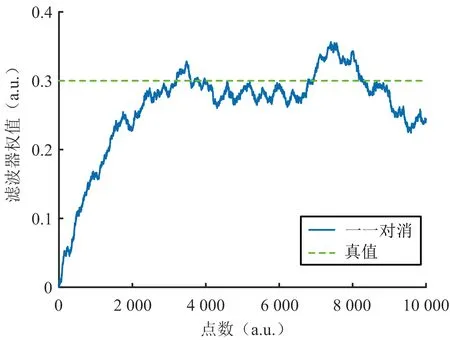
图2 一一对消的滤波器权值收敛

2 联合对消算法

为了消除多信号杂波对消之间的相互影响，本文提出了一种基于LMS的联合对消方法，其原理图如图3所示，相比于一一对消，输入信号为多个同频基站信号的直达波，对回波信号中所有信号源的直达波和多径杂波能量同时进行抵消。

图3 基于LMS的联合杂波对消方法原理

类比式(7)和式(8)有

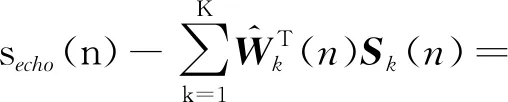
(11)

将式(11)代入式(10)得

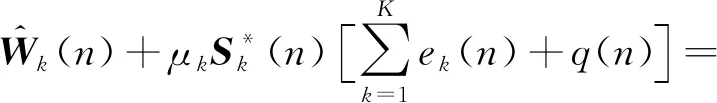
(12)

(13)

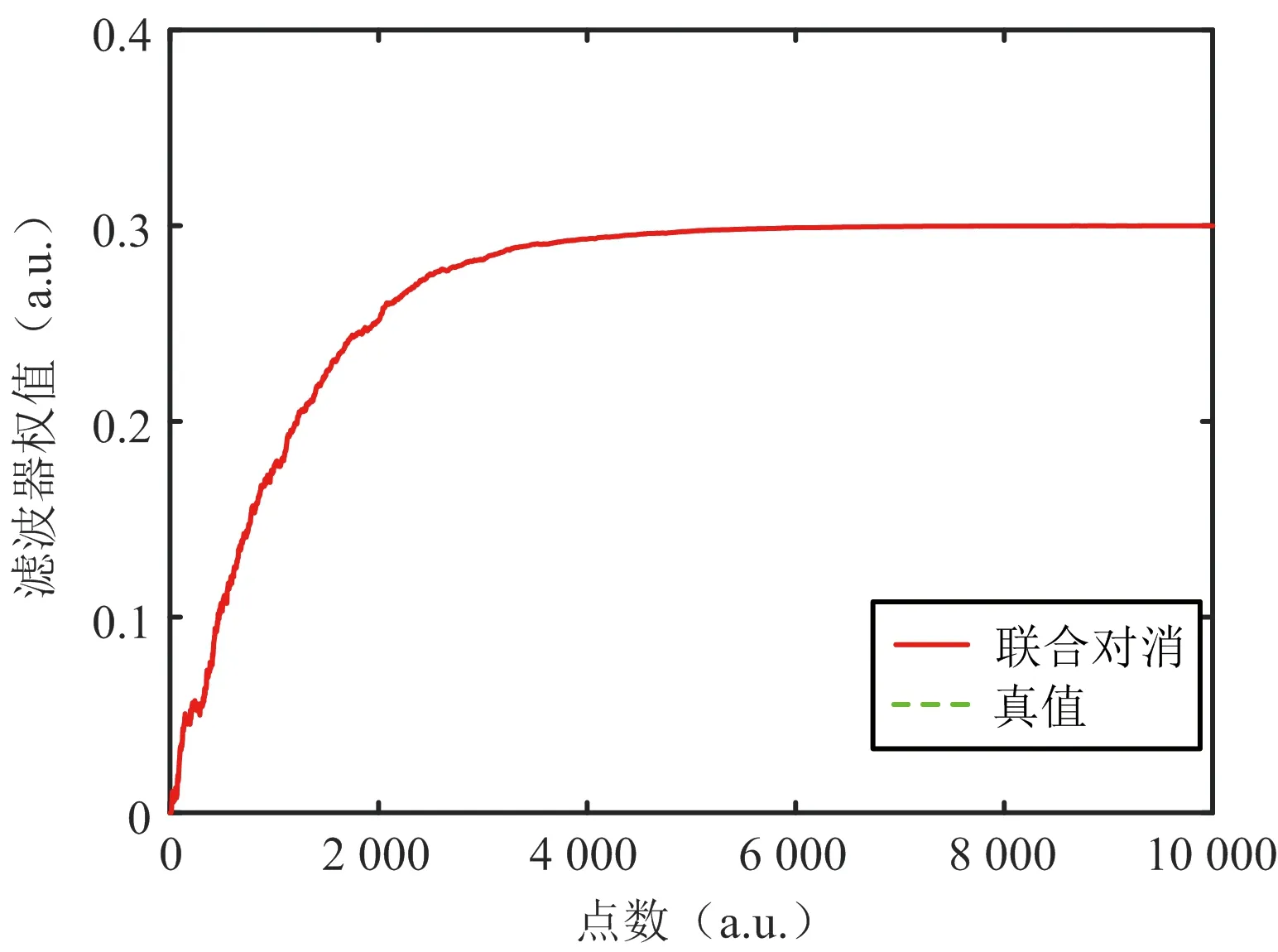
图4 联合对消的滤波器权值收敛

下面定量分析联合对消算法的滤波器权值误差，令

(14)

式中，μk是值都为μk的N维向量，diag[·]表示对角矩阵。联合对消算法的更新公式(式(10)和式(11))可改写为

(15)

对比式(3)和式(15)，这种形式的联合对消算法更新公式和传统对消算法的对消公式相同。定义联合对消滤波器权值误差向量为

(16)

式中，Wo为最优维纳解。则

式(17)表示滤波器权值误差向量ε(n)的随机差分方程，其中

(18)

作为求解随机差分方程的通用方法，此处引入Butterweck迭代过程[16]，在步长参数μk,k=1,2,…,K为小步长时，式(17)的Butterweck迭代过程可表示为

(19)

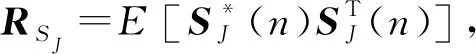
v(n)=QHε(n)

(20)

(21)

将式(20)、式(21)代入式(17)中，并利用QQH=I的性质，得

v(n+1)=(I-μJΛ)v(n)+Φ(n)

(22)

对于联合对消滤波器的第m个自然模式可表示为

vm(n+1)=(1-μ「m/N⎤λm)vm(n)+Φm(n),

m=1,2,…,KN

(23)

式中，「·⎤为向上取整。令vm(0)作为vm(n)的初始值，解式(23)所示的差分方程可得

vm(n)=(1-μ「m/N⎤λm)nvm(0)+

(24)

为保证收敛性，由式(24)易得步长参数需满足0<μk<2/λmax,∀k，λmax是矩阵RSJ的最大特征值。联合对消滤波器的第m个自然模式vm(n)的均值和均方值分别为

E[vm(n)]=(1-μ「m/N⎤λm)nvm(0)

(25)

E[|vm(n)|2]=

(26)

ε1(n+1)=[I-μ1RS1]ε1(n)-

(27)

v1m(n+1)=(1-μ1λm)v1m(n)+Φ1m(n),

m=1,2,…,N

(28)

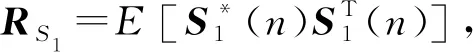
E[v1m(n)]=(1-μ1λm)nv1m(0)

(29)

E[|v1m(n)|2]=

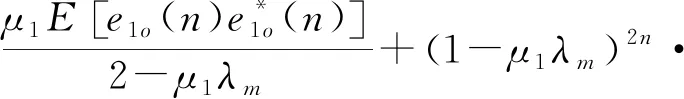
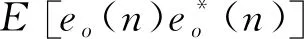
E[q(n)q*(n)]=

E[|q(n)|2]

(31)

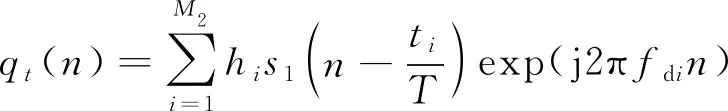
E[|(W1-W1o)TS1(n)|2]+

E[|q(n)|2]

(32)

传统对消方法与联合对消滤波器权值误差均方值的差值为

E[|v1m(n)|2]-E[|vm(n)|2]=

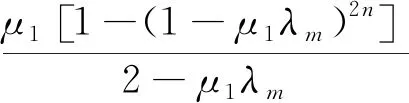
(33)

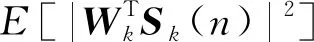
3 频域分块联合对消算法

由于LMS类算法不需要计算有关的相关函数以及矩阵求逆，其计算相对简单，但是无源雷达的目标回波很弱，相对于主动雷达需要更长的积累时间，导致数据量大，且对消阶数高，因此所需要的计算量仍然很大。为了降低计算量，提高实时计算的能力，本文引入了频域分块快速计算[17]的思想，将数据进行分块，使滤波器权值的更新逐块进行，而不再是逐点更新。

SB k(i)=

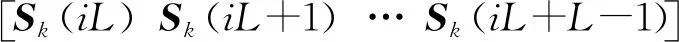
(34)

令

(35)

则第i块输入数据对消后的输出信号E(i)为

(36)

此时式(10)所示的滤波器权值更新公式可改写为按块更新的形式：

(37)

令

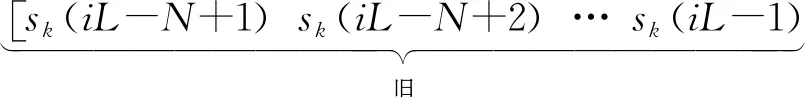
(38)

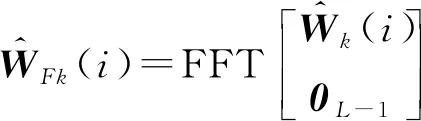
(39)

(40)

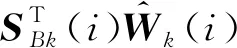
(41)

(42)

则有

(43)

注意到式(39)的后L-1个元素为零，则可将式(37)所示的分块更新公式转换为如下频域形式：

(44)

对于传统的无源雷达杂波对消算法，一一对消每计算一个输出都需要N次乘法，更新一次滤波器权值需要N+1次乘法，因此对于K个直达波信号，L个输出值总共需要(2N+1)KL次乘法。而联合对消FBLMS算法需要2K+1次FFT，2K次IFFT和3K(L+N-1)次乘法，则算法总共所需要的乘法次数为

(45)

在频域分块时，使式(38)新旧两段数据长度相同，即L=N-1，可以使计算效率达到最高，则算法所需乘法总数为(4K+1)Llog2L+(10K+1)L。因此，本文所提算法和传统一一对消算法的复杂度比为

复杂度比=

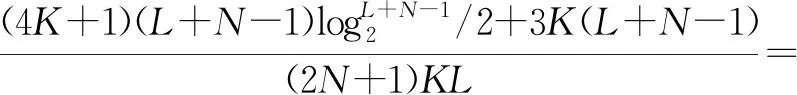
(46)

由式(46)可以看出，复杂度比与辐射源数量和分段长度(或者对消阶数)有关，且辐射源越多，分段长度越大，复杂度比越小，即联合对消FBLMS算法计算效率提升越大。当K=3，对消阶数为2 048时，联合对消FBLMS算法比传统一一对消算法的计算量少约70倍。

4 仿真实验

下面进行仿真分析，假设有两个发射基站，获取到两个直达波信号，回波信号的仿真参数如表1所示。

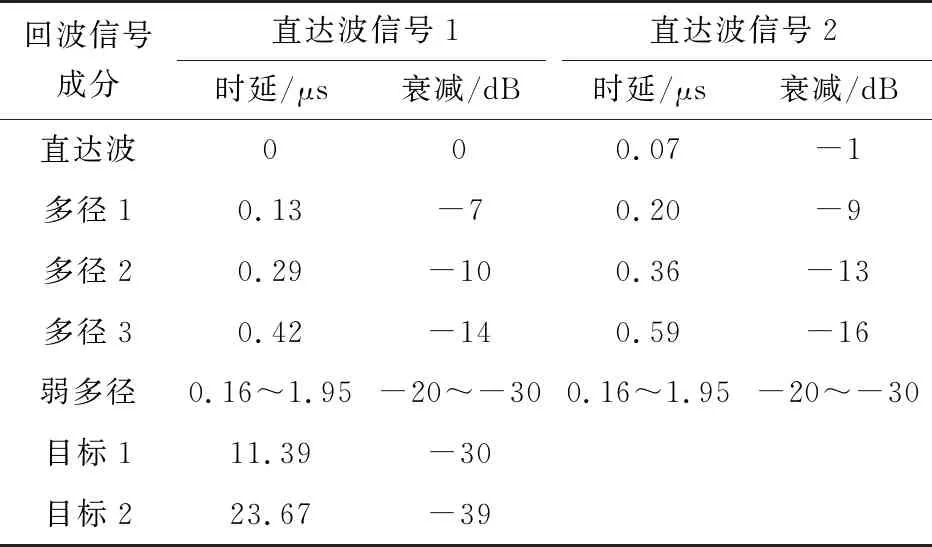
表1 无源雷达回波通道参数

基于频域分块LMS的联合杂波对消算法和传统频域分块LMS一一对消算法(一一对消FBLMS)的滤波器权值收敛比较如图5所示，不妨将真值作为最优解，可明显看出传统方法的收敛结果较差，在最优解附近有较大的波动，而联合对消FBLMS的权值波动较小，基本收敛至最优解。

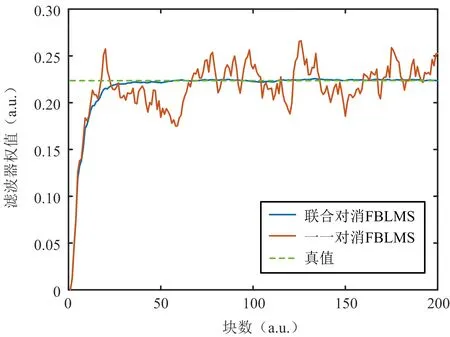
图5 滤波器权值收敛比较

滤波器权值误差的均方偏差学习曲线为

D(i)=E[‖ε(i)‖2]

(47)

则本文所提算法和一一对消FBLMS算法的均方偏差学习曲线如图6所示，联合对消FBLMS的均方偏差更小，在学习曲线收敛后，联合对消FBLMS的均方偏差的均值为9.78×10-5，而一一对消FBLMS的均值为 0.107 2，说明联合对消FBLMS具有更好的收敛特性，所求解的滤波器权值更接近真实值。

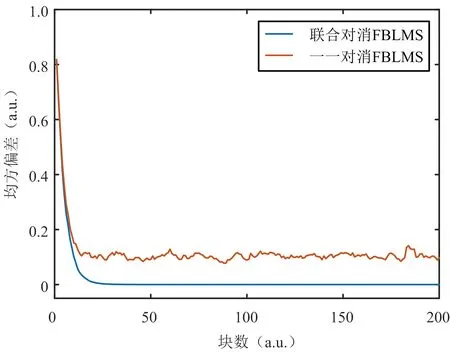
图6 滤波器权值误差的均方偏差学习曲线比较

图7所示为两算法杂波对消能量对比图，其中一一对消FBLMS的杂波对消比为22.84 dB，联合对消FBLMS的杂波对消比为32.35 dB，改善了9.51 dB。且所设仿真参数中的回波信号信杂比为-33.36 dB，联合对消FBLMS的杂波对消比更接近理想值。

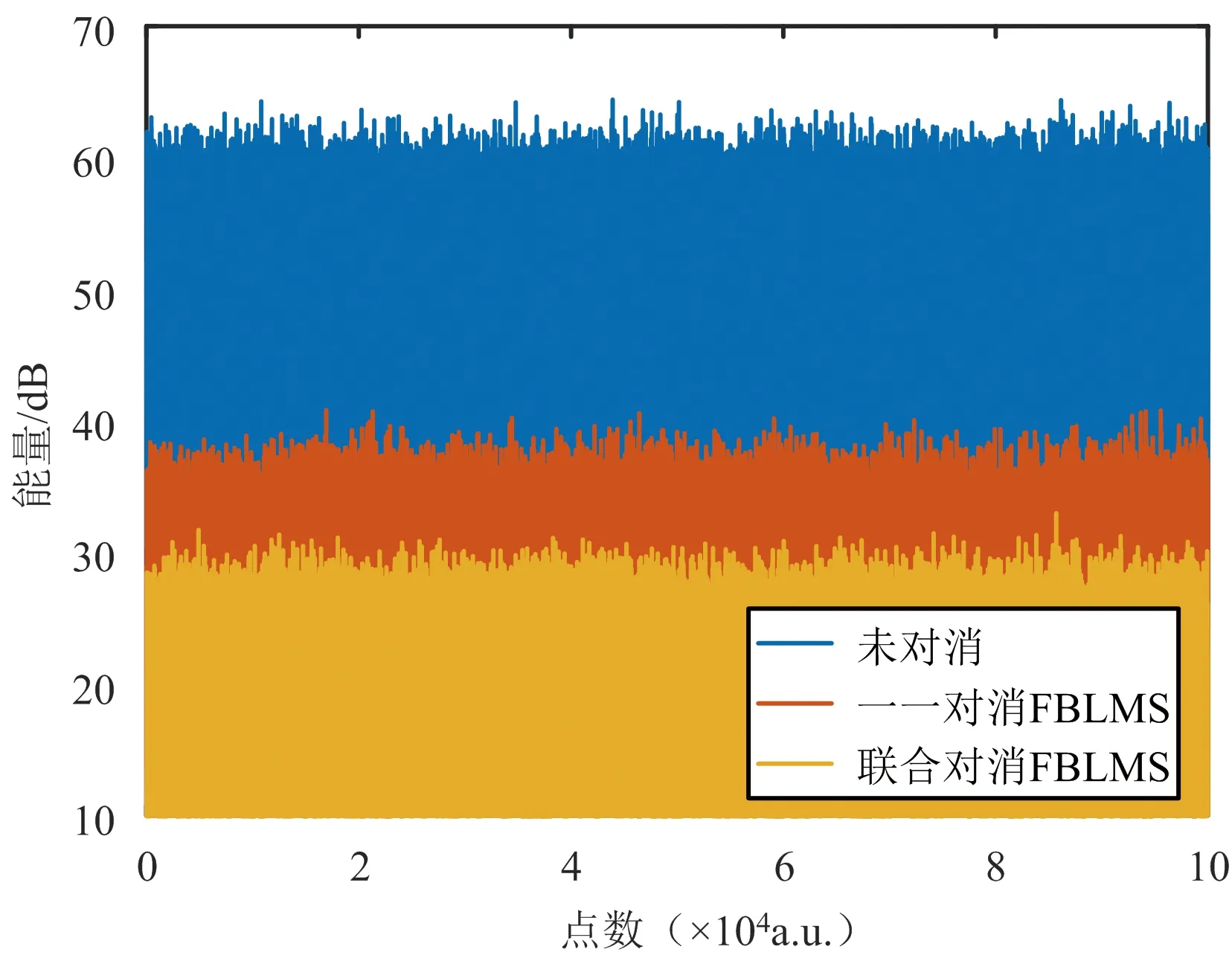
图7 杂波对消能量对比图

杂波对消比的提升对应在互模糊图像上为底噪的降低，如图8所示。图8(a)为原始数据的互模糊图像，未检测出目标，可以观察到近距离的直达波和多径杂波；图8(b)为一一对消FBLMS算法处理后的互模糊图像，底噪为81.51 dB，只检测出11.39 μs处的强目标，目标峰值为100.42 dB，23.67 μs处的弱目标被底噪淹没；图8(c)为联合对消FBLMS算法处理后的互模糊图像，底噪进一步降低至71.86 dB，下降量为9.65 dB，和杂波对消比改善量基本一致，强弱目标都检测出来，峰值分别为100.50 dB和91.59 dB。

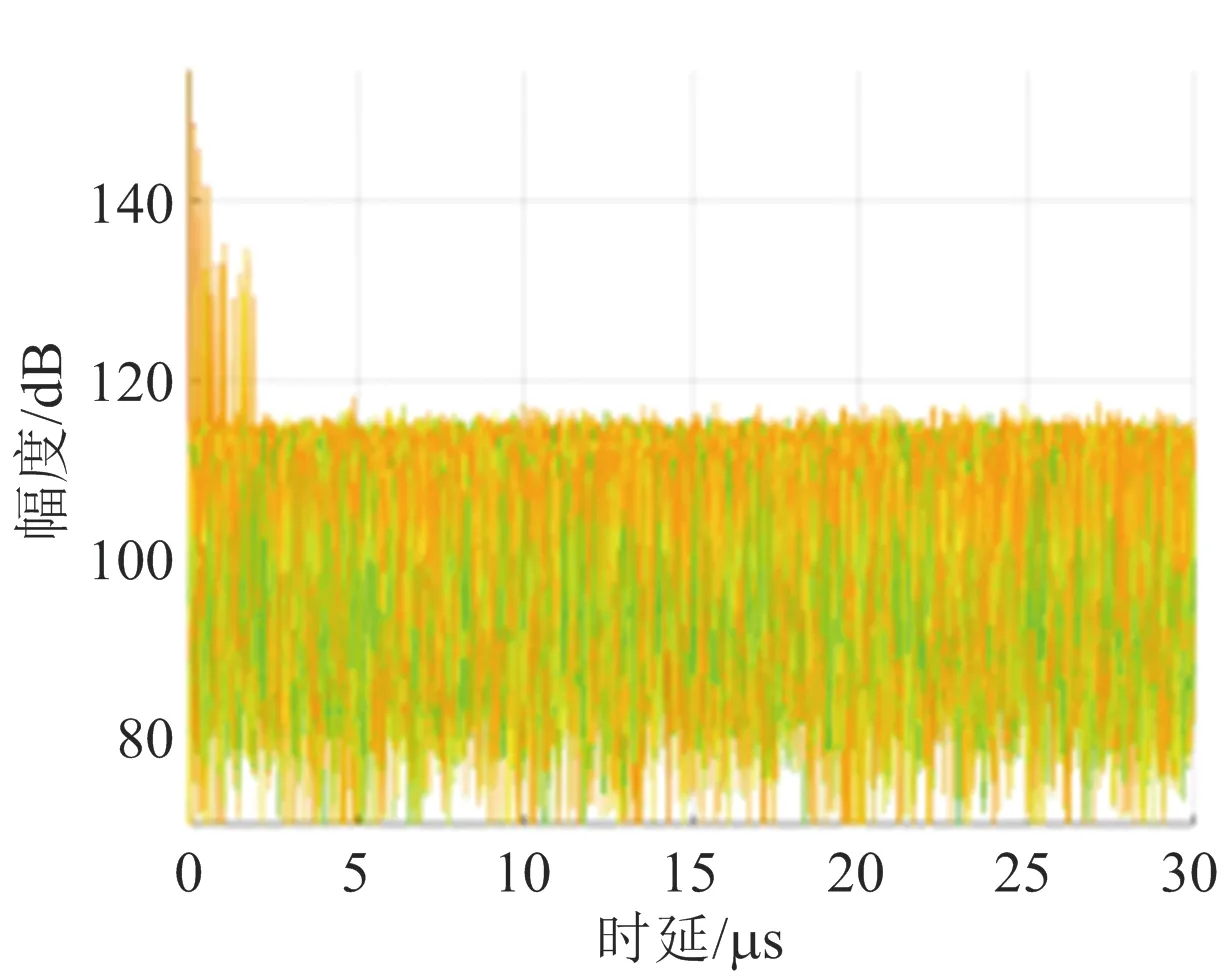
(a) 未处理

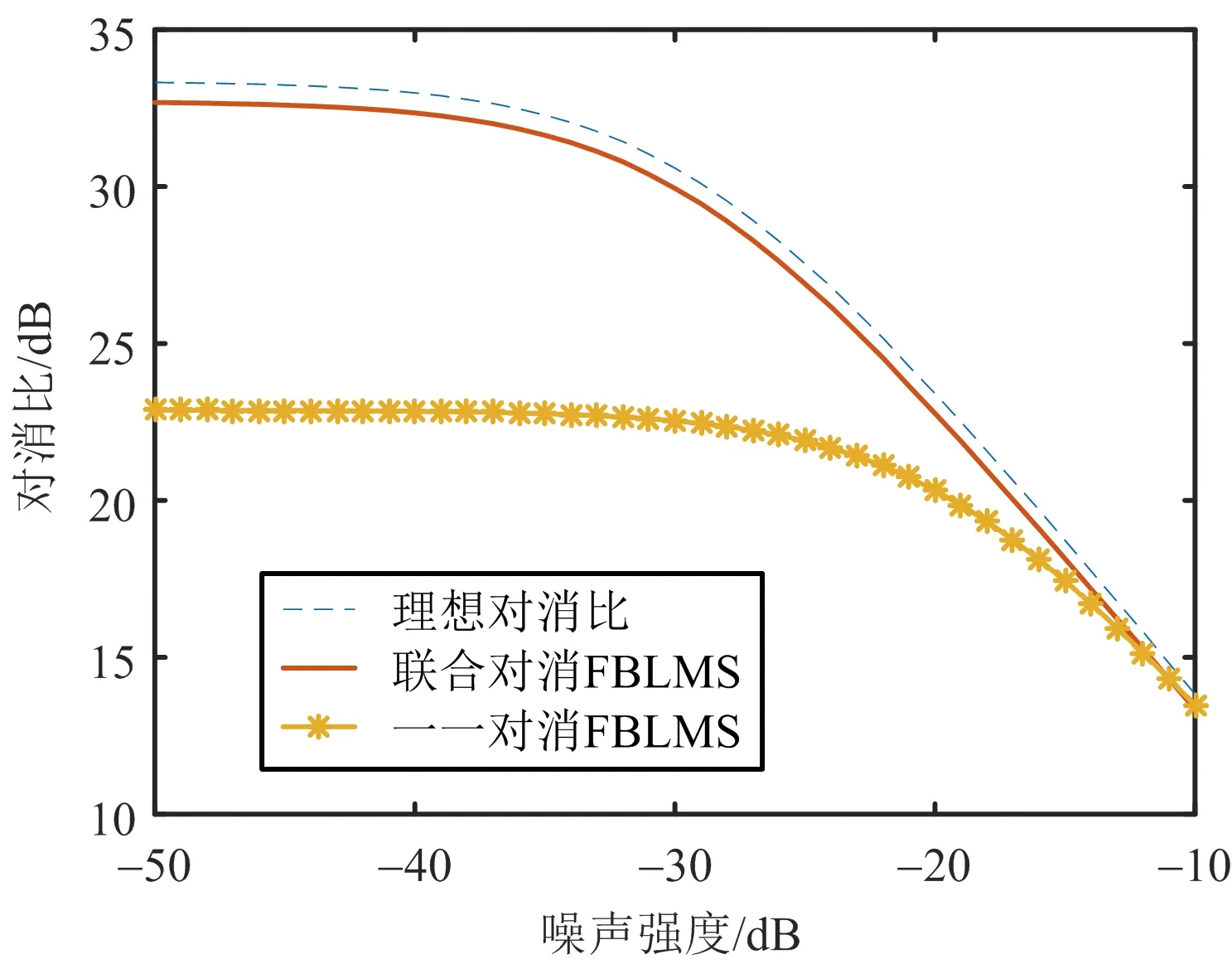
图9 噪声对杂波对消比的影响

联合对消FBLMS的杂波对消比受噪声的影响如图9所示，联合对消FBLMS的杂波对消比接近理想值，有较好的效果。随着噪声的增强，式(4)中q(n)的能量变大，式(12)下等号右侧第三项所产生的干扰变大，因此联合对消FBLMS的杂波对消比随着理想对消比的降低而降低。

从图10可以看出，当分段长度取得足够大时，联合对消的频域分块处理和不分块处理的杂波对消比相差不大，只有分块长度较小时，块内计算步长时的随机性较大，导致滤波器的权值系数无法达到很好的收敛性能，造成杂波对消比的降低。

(a) 整体图

5 结束语

本文针对基于LTE信号的无源雷达对消多个同频基站信号杂波时，传统方法一一对消所存在的问题，提出了一种基于联合处理模型的杂波对消算法，该算法基于LMS算法，将多个同频基站信号作为输入，同时对消所有信号的直达波和多径杂波，解决了传统对消方法一一对消时，后对消的信号影响先对消信号的滤波器权值收敛，造成收敛误差大的问题，提升了杂波对消比。通过频域分块处理，利用FFT进行快速计算，有效地降低了计算复杂度。通过仿真分析，该算法有效提升了对消滤波器权值的收敛性能，能够更逼近最优解，提升了杂波对消比，降低了互模糊函数的底噪，改善了基于LTE信号无源雷达的检测性能。