基于特征辅助的滑窗式全局最优关联算法

陈 姝，关 欣，胡玉新

(1. 中国科学院空天信息创新研究院，北京 100094；2. 中国科学院空间信息处理与应用系统技术重点实验室，北京 100190；3. 中国科学院大学，北京 100049)

0 引言

近年来，随着星载无源探测技术的发展，电子信号探测正由单星探测向多星组网发展，多星协同电子目标探测与跟踪成为可能。多星协同较单星探测可实现对同一地区的长时间连续观测，其应用与工程需求日渐迫切。多星协同数据处理的一项核心问题是判断多星获取的同一电子目标关联关系。因此，精准高效的多源电子目标关联是多星无源探测的关键技术之一。

无源探测系统主要获取雷达等辐射源设备的运动与电磁特征参数信息。根据数据关联算法对不同类型信息的利用情况，算法可大致分为两类：基于运动信息、综合运动与特征参数的关联算法。常见的基于运动信息的关联算法包括NN算法[1-2]、JPDA算法[3-5]与GNN算法[6-9]等。在综合信息关联算法中，现有算法多是利用特征参数的相似性对位置关联结果进行修正，利用目标运动状态和特征参数之间的互补性，构造综合关联矩阵[10-19]。文献[12-17]重点探讨了结合目标特征的最邻近关联滤波算法与联合概率数据关联算法，目标特征参数的选择包括载频、脉宽、幅值以及目标的尺寸等，为辐射源特征参数用于提升算法性能提供了思路。文献[18]将综合性线段Hausdorff距离灰色关联理论应用于航迹关联，提出基于特征辅助的灰色航迹关联方法，充分利用了量测的有用信息。文献[19]提出了一种基于辐射源综合参数的多维可变跟踪门，运用模糊多门限思想的无源关联算法，解决关联时复杂度高，计算量大的问题。

无源定位系统探测过程中噪声干扰强、定位精度不高且多星间数据精度有差异、重访间隔不一、信息不连续、目标缺失概率大[20-21]。针对其数据特点及综合信息关联算法中存在的重关联、误关联、杂波干扰大及特征参数改变带来的权重影响等问题，本文基于综合信息，提出一种滑窗式全局最优航迹关联算法，简称SGDA(Sliding Window Global Optimal Data Association)。算法通过计算综合相似度构建关联模型，采用全局最优思想求解得到最优航迹关联对，同时利用滑窗处理技术修正错漏航迹，维持与监测已确认航迹，从而降低系统误差、噪声干扰与特征参数改变对关联的影响，提高算法性能。

1 数据关联基本原理

常用的数据关联方法主要包括最邻近法与联合概率数据关联法等。最邻近算法运算量小，模型简单有效，易于实现，但在密集多目标环境中，容易跟错目标。JPDA的基本思想是利用贝叶斯推理计算观测数据与每一个目标之间的关联概率，适用于杂波环境下的密集机动目标跟踪，但当目标和量测数目增多时，算法计算量将出现组合爆炸现象，导致计算复杂。

在最邻近算法中，通过计算各测量值的加权统计距离dij，即

(1)

(2)

JPDA的基本思想是利用贝叶斯推理计算观测数据与每一个目标之间的互联概率。根据互联概率决定测量值在目标状态更新中的权重。令θit表示量测i源于目标t事件，Zk表示量测值，假设在时刻k接收到mk个量测，则第i个量测与目标t的关联概率βit可定义为

βit=P{θit(k)|Zk},

i=0,1,…,mk;t=0,1,…,T

(3)

则k时刻目标t的状态估计如下：

(4)

由此得到综合观测值为

(5)

2 SGDA算法描述

2.1 综合关联度

假设不同卫星电子信息的两次观测，在观测1中探测到多个目标的集合群S1，其中含有n1个目标(a1,a2,…,an1)，在观测2中探测到群目标S2，其中含有n2个目标(b1,b2,…,bn2)。由于存在非共同观测目标、虚警点以及观测缺失，n1和n2不一定相等。对于群目标S1中的任意目标k，用Ask=(akf,akr,akw)，k=1,2,3,…,n1描述第k个目标的电磁特征参数向量，其中akf为载频均值，akr为脉冲重复间隔均值，akw为脉宽均值；用Adk=(akLAT,akLON)，k=1,2,3,…,n1描述第k个目标的经纬度信息。同理，用Bsk与Bdk描述群目标S2的电磁特征参数矢量与位置信息。

对目标的经纬度进行标准化处理，得到S1内的目标am和S2内的目标bn之间的统计距离为

(6)

式中α1，α2为权重，且α1+α2=1。

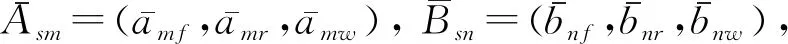
(7)

基于位置与特征参数的航迹关联就是判断两目标间的综合相似度大小，而目标相似是一个模糊的概念，通过模糊数学中的加权平均来计算其相似度大小，这是一种定量的处理方法，公式如下：

D(m,n)=λ*dp(m,n)+(1-λ)*dl(m,n)

(8)

(9)

式中，λ为位置统计距离所占权重，D(m,n)为综合统计距离，γmn为综合相似度。

由此可建立观测1、2间的关联矩阵：

(10)

其中γmn值越大，S1内的目标am和S2内的目标bn之间的关联程度则越高。

2.2 全局最优关联判决

由于对关联矩阵直接求最大值时[8,22]，没有考虑到不同目标的估计结果的影响，因此会发生重复关联、误关联的情况，所以其结果是次优的。针对这个问题，本文在根据关联矩阵求目标关联对时，采用全局最优的思想，将各观测值与所有目标辐射源关联度作为信息源进行全局最优估计，从而得到最佳航迹关联对。根据式(10)建立的关联矩阵Cn1×n2，建立以γmn为关联度，L(i)为目标函数的关联模型，求解全局最优的航迹关联关系：

L(i)=argmaxCn1×n2,i=1,…,n1

(11)

求解模型关键在于获取最大可能的关联事件，确定量测与目标的对应关系，可转化为典型的二维指派问题，二维指派问题的求解方法很多，在这里采用性能更高的JVC算法[9]。

这里将m个量测值分配给n个目标，其中m≤n2,n≤n1，分配原则如下：

(12)

其中：观测点j分配给航迹i时，ηij=1；否则，ηij=0。

由于不同时刻观测数据间存在非共同观测目标，因此其关联度还需要经过关联门限ε的检验，即关联度满足门限要求的关联对才被确认为航迹关联对，ε的取值可由仿真确定。

2.3 滑窗式全局最优关联

在密集杂波环境下，当雷达工作模式发生变化时，关联算法容易发生误跟、漏跟的现象，因此本文采用时间滑窗式思想，在全局最优航迹关联的基础上，确定航迹关联对，修正连续判决结果，改善辐射源工作模式变化时关联误差大的问题。

假设某一确认航迹i的辐射源参数aif,air,aiw在下一节点发生改变，根据式(6)～式(9)求得的γmn发生突变，且γmn>ε，此时，确认航迹容易与杂波误关联。下一时刻，误关联航迹可能继续跟错目标，导致航迹连续失真，从而被判断成虚假航迹或航迹终止，也可能关联回正确航迹。其关联结果受杂波影响较大。为减少这种误差现象，引入滑窗关联质量参数来修正错漏关联结果，提高算法的稳健性，其示意图如图1所示。定义mij(k)为k时刻航迹i与观测点j的滑窗关联质量，即

(13)

式中，M为滑窗长度。如果满足mij(k)≥N，N为质量门限，则确认航迹i与观测点j为航迹关联对。M，N取值可由仿真确定，一般可取M=5，N=3，此时对误差关联的容忍度为40%。

图1 滑窗式全局最优关联

2.4 算法流程

系统k时刻状态方程和量测方程用矩阵形式可表示为

X(k)=F(k)X(k-1)+W(k)

(14)

Z(k)=H(k)X(k)+V(k)

(15)

式中，F(k)为状态转移矩阵，H(k)为量测矩阵，W(k)与V(k)分别为具有协方差矩阵Q(k)和R(k)的过程噪声与量测噪声。

本文算法流程的主要步骤如下：

步骤1 目标状态输入及模型预测。模型i在k+1时刻的输入为k时刻滤波器输出的估计值结果。目标状态与量测的一步预测：

(16)

(17)

预测协方差：

Pi(k+1|k)=F(k)Pi(k|k)[F(k)]T+

Q(k-1)

(18)

步骤2 建立椭圆跟踪波门，确定量测是否有效，其波门规则如下：

(19)

步骤3 滑窗式全局最优航迹关联判决，根据式(6)～式(13)，计算第j个量测对目标i的关联概率μji(k)，求得最优量测与目标配对关系：

(20)

步骤4 根据观测匹配点Zj更新模型。对应模型j(j=1,…,n2)状态估计与估计误差协方差更新：

(21)

Pi(k+1|k+1)=

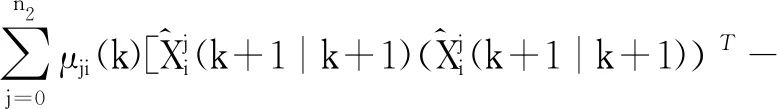
(22)

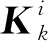
3 仿真与分析

3.1 仿真条件

模拟仿真场景为294 km×335 km范围的海域，该区域中存在26艘船只，每艘船搭载的雷达辐射源种类、数量不尽相同，总共包括39部雷达，17种雷达类型。观测过程中，雷达的工作模式不变或发生改变，其运动状态包括运动与静止状态。多星进行观测的时间间隔为30 min。部分辐射源参数信息如表1所示，其中变化次数表示任务时间内工作模式变化的次数。

假设卫星随机截获目标辐射的雷达信号，卫星对该区域持续观测时间为5 min。取30次卫星观测任务的观测数据进行实验分析。卫星观测数据的参数测量精度以叠加均值为0，标准差取各特征值4%的高斯噪声来模拟，卫星定位精度为2 km。观测数据中存在1 000个杂波点，杂波点的位置在294 km×335 km范围内服从均匀分布，其特征参数同样服从均匀分布，其参数信息如表2所示。

表1 部分辐射源参数信息

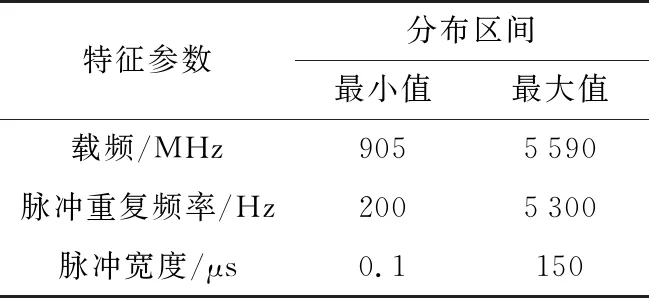
表2 杂波数据的参数信息

3.2 仿真结果及分析

取连续观测任务1、2的观测数据进行实验分析，采用SGDA算法进行目标关联，实验结果如图2所示。图2中，黑色点迹为杂波点，红色点迹为目标点迹，蓝色点迹为目标下一步的观测点迹，连续任务间的多目标关联结果如连线情况所示。由图2可知，SGDA算法可实现多源电子目标关联的基本要求，确定目标的下一量测更新，同时有效抑制杂波影响。

图2 连续两任务间目标关联结果示意图

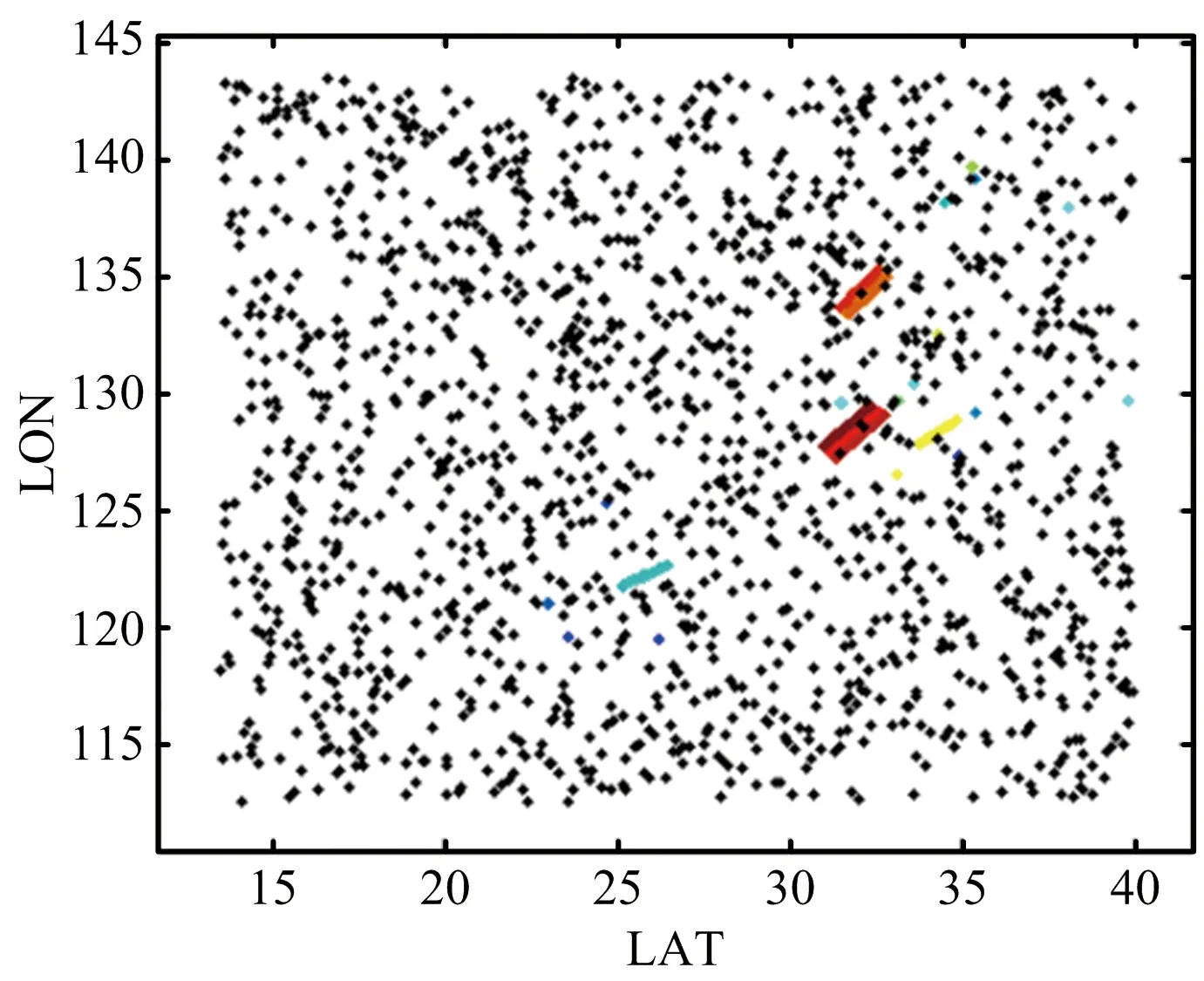
(a) 连续多任务间关联结果示意图

对上述所有观测任务进行关联分析，得到的目标关联结果如图3所示。其中图3(a)中，黑色点迹为杂波点，彩色航迹为观测目标关联结果；图3(b)为图3(a)中某一编队上辐射源关联结果细节放大图。由图3(a)可知，在抗杂波干扰的同时，SGDA算法可对不同型号雷达进行区分，有效判断有效航迹的条数。从图3(b)可知，对于同一编队里不同舰船上搭载的同类型雷达，在距离相近且特征参数类似的情况下，该算法避免了目标误关联的现象，同时有效地区分了同平台的多部雷达，改善了多目标情况下关联误差大的问题。

针对特征参数改变带来的权重影响问题，取观测过程中某一船只上特征参数发生改变的雷达观测数据进行实验分析，观察当辐射源特征参数发生变化时，SGDA算法、基于特征参数的NN算法、基于特征参数的JPDA算法、传统的NN算法与JPDA算法的性能情况。表3给出了100次蒙特卡罗实验下各关联算法的关联正确率与程序运行时间。

表3 辐射源特征参数改变时各算法性能比较

从表3可知，当雷达辐射源特征参数发生变化时，基于特征参数的NN算法关联正确率较低，甚至低于NN算法，说明雷达辐射源特征参数改变对原本利用特征参数修正NN算法的结果带来了较大的干扰，其关联误差增大；而基于特征参数的JPDA算法的正确率高于JPDA算法，但低于SGDA算法，说明相较于某节点特征参数改变带来的关联误差，特征参数用于修正JPDA算法结果的作用更大，但仍会带来关联误差，因此其正确率低于SGDA算法。本文提出的SGDA算法的关联精度均高于其他算法，且计算量低，说明其在辐射源特征参数改变时，仍能有效关联跟踪，保证了算法的稳健性与准确性。

针对上面给出的仿真条件，分别运用上述算法对一定范围的所有观测目标进行关联跟踪，表4为100次蒙特卡罗实验下各关联算法跟踪失败次数、目标关联正确率与程序运行时间比较情况。图4为不同目标在各关联算法下的均方根误差比较情况。

从表4和图4的分析可知，NN算法的关联正确率最低，且得到的估计均方根误差最大，但其计算量低。基于特征参数的NN算法无论在关联误差还是均方根误差上对比NN算法均有较大程度的改进。传统JPDA算法在密集目标环境下的性能明显优于NN算法。基于特征参数的NN算法相较于JPDA算法的均方根误差较大，但其关联正确率高，且计算量低。基于特征参数的JPDA算法相较于JPDA算法大幅提升了关联精度，计算量与估计均方根误差两者差异不大。SGDA算法相较于基于特征参数的NN算法，计算量差异不大，但其关联精度得到了大幅度提升，且其估计均方根误差较小；相较于基于特征参数的JPDA算法，关联精度略高，计算量大幅度降低，两者均方根误差差异不大，但SGDA算法中少数目标的误差估计存在突变现象。

表4 各关联算法性能比较

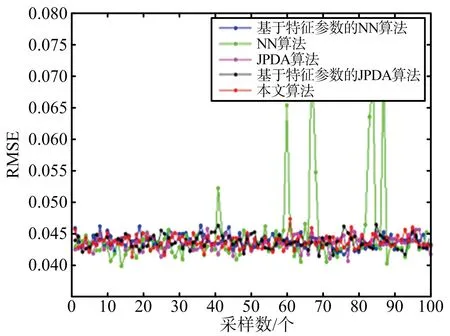
(a) 目标1的均方根误差比较

综上所述，SGDA算法相较于其他算法，在降低计算复杂度，提高信息利用率的同时，提升了目标关联的精度，虽然均方根误差在雷达特征参数改变时容易发生突变，但算法综合性能得到了提升，可满足对近距离交叉目标、存在非共同观测目标和杂波密集环境下多目标的有效跟踪。

4 结束语

本文在传统的关联算法基础上，提出了一种基于特征参数辅助的滑窗式全局最优多源数据关联算法(SGDA)。算法以量测与目标的综合相似度替代可行联合事件概率的计算，更加充分地利用目标的量测信息，对关联模型进行全局最优求解，改善多目标在密集杂波环境下的重关联、误关联以及杂波干扰大的问题，同时针对特征参数带来的权重影响，采用滑窗处理技术对航迹进行错漏修正与维持。仿真验证了算法的有效性，算法适用于多源卫星电子在密集杂波环境下的关联跟踪，可确保目标跟踪的准确性与稳定性，具有实用意义。