改进重度增加法在岩质边坡稳定分析中的应用研究

赵晨凯，李连营，杨笑男

(天津市勘察院，天津 300000)

目前强度折减法和重度增加法是边坡稳定分析中的常用方法。强度折减法固定荷载不变，通过采用对边坡抗剪强度进行折减的方式使其达到临界失稳状态，以边坡初始强度和临界强度的比来定义边坡的安全系数。如陶宇等[1]基于强度折减法研究了传统的边坡失稳三大判据在二维均质和非均质边坡中的适用性问题；王曼等[2]基于强度折减法分析了某边坡从局部到整体的失稳过程；李庶林等[3]基于强度折减法对某高陡边坡在自然状态及使用预应力锚索、锚杆等加固措施后的稳定性问题进行了分析。重度增加法不改变边坡现有强度，通过增加荷载的方式使边坡达到临界失稳状态，以临界荷载与标准荷载之比来定义边坡的安全系数，但当边坡摩擦角较大时，计算出的安全系数偏大，针对这一问题，研究人员对此方法进行改进，从而得到了改进重度增加法[4]。张文圣等[5]基于改进重度增加法分析了某三维均匀土坡的稳定性；赵坤鹏等[6]采用改进重度增加法对某边坡在自然状态及抗滑桩加固后稳定性问题进行了分析；牟声远等[7]经研究发现改进重度增加法分析粘性土及岩质边坡的稳定问题是可行的。本文基于ABAQUS采用改进重度增加法对某岩质边坡的稳定性进行了分析，并与强度折减法和极限平衡法得出的结果进行对比。

1 计算理论与方法

1.1 改进重度增加法

改进重度增加法固定边坡现状抗剪强度参数(c、φ)不变，增加重力加速度的同时对内摩擦角进行同等程度的折减，计算公式如下：

(1)

定义边坡达到临界失稳状态时对重力加速度的增加程度F为安全系数。

1.2 强度折减法

强度折减法固定荷载不变，把边坡现状抗剪强度参数(c、φ)等比例折减k倍，然后用折减之后的边坡抗剪强度参数(c1、φ1)进行分析，计算公式如下：

(2)

定义边坡达到临界失稳状态时对边坡抗剪强度参数(c、φ)的折减程度k为安全系数。

1.3 失稳判据

边坡失稳判据主要有：(1)计算不收敛判据；(2)位移突变判据；(3)塑性区贯通判据。为了确保计算结果的准确性，本文综合考虑关键点的位移及塑性区的分布情况对边坡的稳定性进行分析。

2 实例分析

2.1 计算模型

某岩质边坡概化模型如图1所示，边坡浅层表面为强风化区。模型底部长1 400 m，总高度为800 m，基座厚度为250 m，边坡高550 m。强度准则选取Mohr-Coulomb准则，具体材料参数见表1。

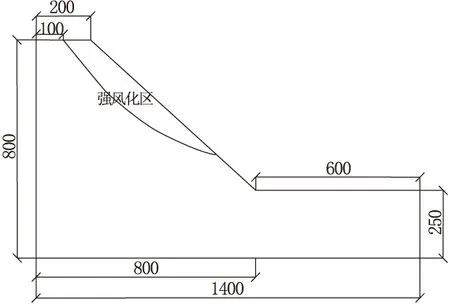
图1 边坡模型

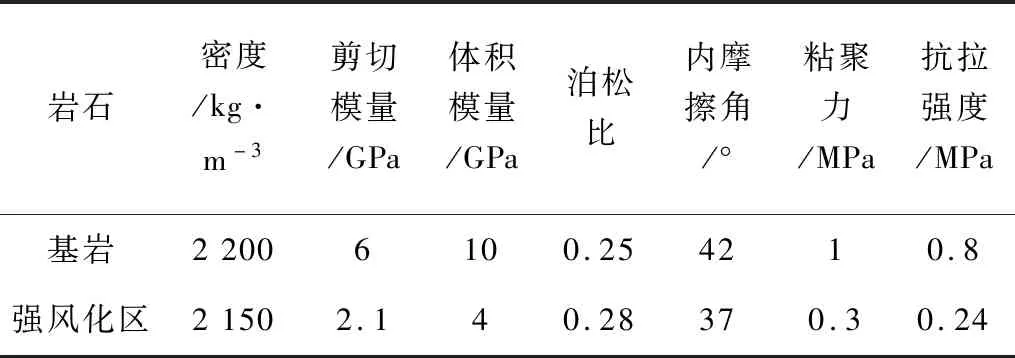
表1 边坡材料物理力学参数表

2.2 改进重度增加法结果分析

2.2.1 位移突变判据

提取坡顶关键点的水平向位移并绘制与重度增加系数F的关系曲线(图2)，从图中可以看出当重度增加系数F=1.21时，关键点位移发生突变，从位移突变的角度可以判定该岩质边坡的安全系数为1.21。

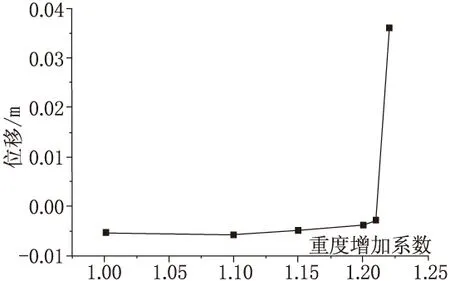
图2 关键点位移与重度增加系数关系曲线

2.2.2 塑性区贯通判据

随着重度增加系数的增大，边坡受到的荷载越来越大，塑性区从最薄弱的地方慢慢开展直至贯通。如图3所示，当F =1.1时，塑性区只产生于强风化区下部一小块区域内，随着F的不断增大，塑性区在慢慢向坡顶扩展；当F =1.21时，塑性区延伸到坡顶，边坡产生了贯通坡顶和坡脚的滑裂带。

图3 边坡塑性应变云图

综合关键点位移突变判据和塑性区贯通判据结果可以判定，该边坡的基于改进重度增加法计算出的安全系数为1.21。

2.3 强度折减法结果分析

2.3.1 位移突变判据

提取坡顶关键点的水平向位移并绘制与折减系数k的关系曲线(图4)，从图中可以看出当折减系数k=1.22时，关键点位移发生突变，从位移突变的角度可以判定该岩质边坡的安全系数为1.22。

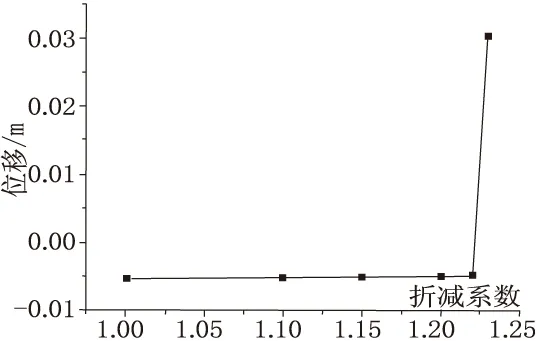
图4 关键点位移与折减系数关系曲线

2.3.2 塑性区贯通判据

随着折减系数的增大，岩土材料在不断软化，塑性区从边坡最薄弱的地方慢慢开展直至贯通。如图5所示，当k =1.1时，塑性区只产生于强风化区下部小块区域内，随着k的不断增大，塑性区在慢慢向坡顶扩展；当k =1.22时，塑性区延伸到坡顶，边坡产生了贯通坡顶和坡脚的滑裂带。

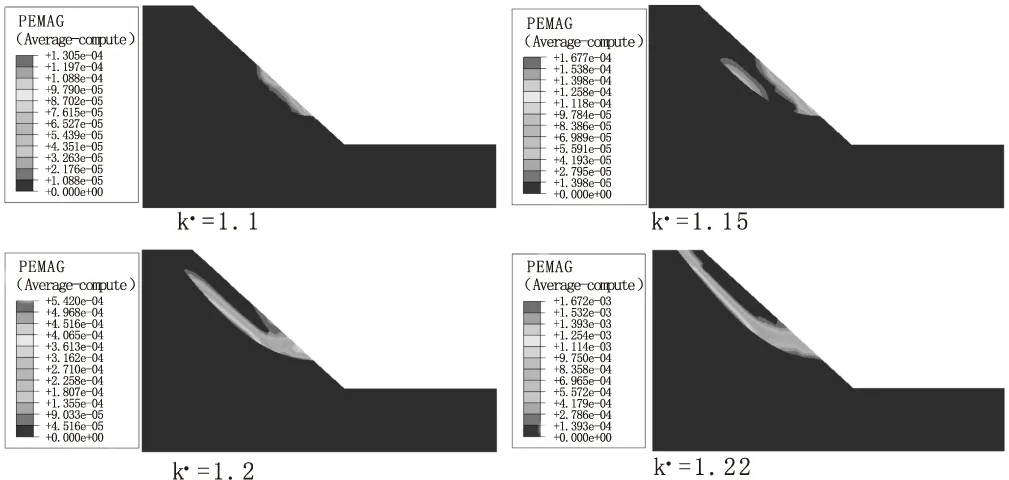
图5 边坡塑性应变云图

综合关键点位移突变判据和塑性区贯通判据结果可以判定，该边坡的基于强度折减法计算出的安全系数为1.22。

2.4 结果对比分析

本文根据摩根斯顿-普赖斯(Morgenstern-Price)法、毕肖普(Bishop)法、简布(Janbu)法计算出了该边坡的安全系数分别为1.226、1.23、1.169，与上文改进重度增加法和强度折减法得出的结果进行汇总得到表2。

从表2可以看出，改进重度增加法计算出的安全系数为1.21与强度折减法计算的安全系数1.22以及三种极限平衡法给出安全系数区别不大，证明了改进重度增加法的可行性和计算精度。

表2 不同方法下的边坡安全系数

3 结语

(1)在岩质边坡计算出，改进重度增加法计算出的结果与强度折减法和极限平衡法计算出的结果相差不大，验证了改进重度增加法的可行性和计算精度。

(2)建议在确定边坡安全系数时综合考虑位移突变判据和塑性区贯通判据结果。