互补总体经验模态分解方法在回转窑故障检测中的应用

周昀逸，张 云

(1.武汉理工大学 机电工程学院，湖北 武汉 430070;2.武汉理工大学 建材行业回转窑检测技术中心，湖北 武汉 430070)

回转窑作为大型重型旋转机械，各部件间存在强耦合特性，故障机理较为复杂[1]。大齿圈作为回转窑关键的传动装置之一，对回转窑窑体的平稳运行起着重要作用。

当回转窑发生筒体热弯曲故障时，一般会引起大齿圈振动。因此，大齿圈径向位移(振动)信号中包含了回转窑筒体热弯曲故障信息，通过对大齿圈径向位移信号进行分析，理论上能够对回转窑工况进行识别。笔者采用电涡流位移传感器来获得大齿圈径向位移信号。然而，由于现场环境恶劣，采集的实际信号表现出非平稳性，通过简单的傅里叶分析只能得到信号时间历程的平均化[2]，无法从原始信号中准确提取出故障信息。Huang等在对瞬时频率概念进入深入研究后创造性提出了固有模态函数(intrinsic mode function,IMF)和将任意信号分解为固有模态函数组成的新方法，这就是经验模态分解(empirical mode decomposition，EMD)[3]。EMD方法具有绝对的自适应性，能够运用于不同场合，胡昭中等运用 EMD 方法处理托轮振动信号[4]和筒体外轮廓信号[5]，分析筒体的故障类型。然而，在对信号进行EMD的过程中，也伴随着模式混叠的问题：在同一个IMF里会有不同尺度的信号混杂，或者是某一尺度的信号出现在不同的IMF中。为了解决EMD存在的问题，2009年，Wu等提出了噪声辅助的集合经验模态分解方法(ensemble empirical mode decomposition,EEMD)，加入白噪声来解决模式混叠问题[6]。虽然EEMD方法能够较好地解决模式混叠问题，弥补了EMD方法的不足，但是得到的IMF中无法避免的会夹杂着少许噪声信号。针对以上问题，Yeh等[7]提出了互补总体经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)方法，该方法与EEMD类似，唯一不同的是，在对原始信号添加高斯白噪声的同时，会对另外一组完全相同的原始信号添加一个幅值相同但是方向相反的白噪声信号，然后对这两组信号进行EMD，最后集总平均得到原始信号的各个IMF分量[8]。这种方法不仅能够解决单纯EMD的“模式混叠”问题，还能够减少EEMD中白噪声所造成的影响。

笔者提出一种基于CEEMD的回转窑大齿圈径向位移信号的特征谐波提取方法，将CEEMD应用到大齿圈齿顶径向位移信号的数据处理中，首先，验证实际信号中存在与筒体工频一致的特征谐波KH(kiln harmonic)；然后，将CEEMD与其他信号处理方法的结果进行比对；最后，结合该方法与其他故障检测方法，找到了KH与筒体弯曲故障之间的关系，确定KH包含有筒体弯曲故障信息，验证了该方法用于故障检测的可行性。

1 互补总体经验模态分解

CEEMD方法是建立在EMD方法基础上的一种信号处理方法，通过EMD可将原始信号分解为若干个IMF，其中IMF必须要满足两个条件[9-10]：①整个信号中，零点数目与极值点数目相等或至多相差1；②信号任意一点上，由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值均为零。EMD算法流程如图1所示。

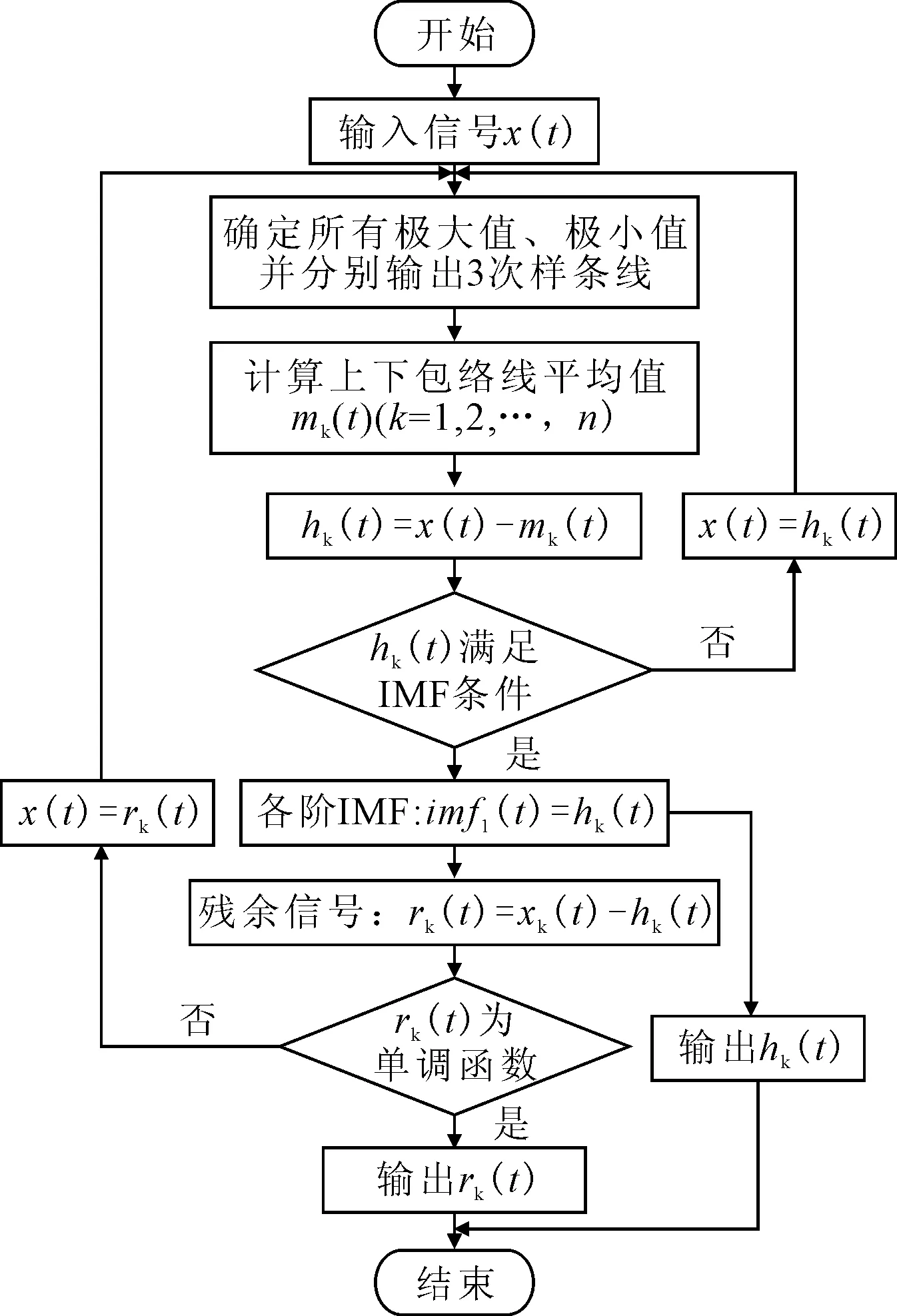
图1 EMD算法流程图

CEEMD方法的算法原理如下：

(1)将一对幅值相等、方向相反的白噪声ni(t)添加到原始信号x(t)中，可以得到两组信号Pi(t)、Ni(t)。

(1)

(2)对Pi(t)，Ni(t)进行EMD处理，可以分别获得j个IMF分量(k=1,2,…,j)，即：

(2)

(3)求出2n次分解后各阶IMF的平均值，可以得到各阶IMF为：

(3)

其中，i=1,2,…,n，2n表示分解次数。

2 几种不同信号处理方法的对比分析

笔者以某铝厂调整后的大齿圈径向位移信号x6(t)作为EMD、EEMD、CEEMD算法的实验对象。测量系统包括上位机软件、NI数据采集卡和电涡流位移传感器。

在测量现场中，筒体自转周期为45 s,采样率为100 Hz，在回转窑调整过程中，按照时间先后采集了6组齿顶径向位移信号，其中第一组表示调整前的信号x1(t)，第六组表示调整后的信号x6(t)。以x6(t)为实验对象，分别采用EMD、EEMD、CEEMD，可以得到不同信号处理方法下的分解结果，其中图2为EMD的分解结果，图3为EEMD分解结果，图4为CEEMD的分解结果。

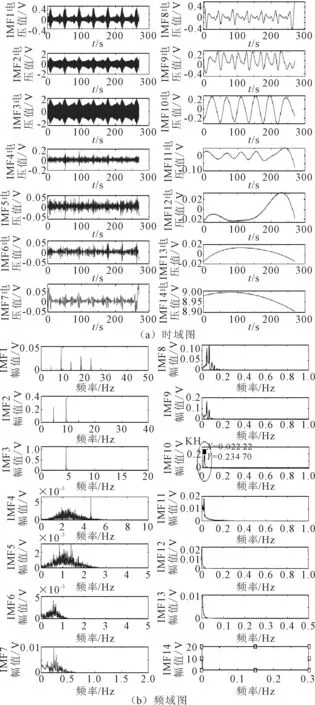
图3 实际信号x6(t)的EEMD结果

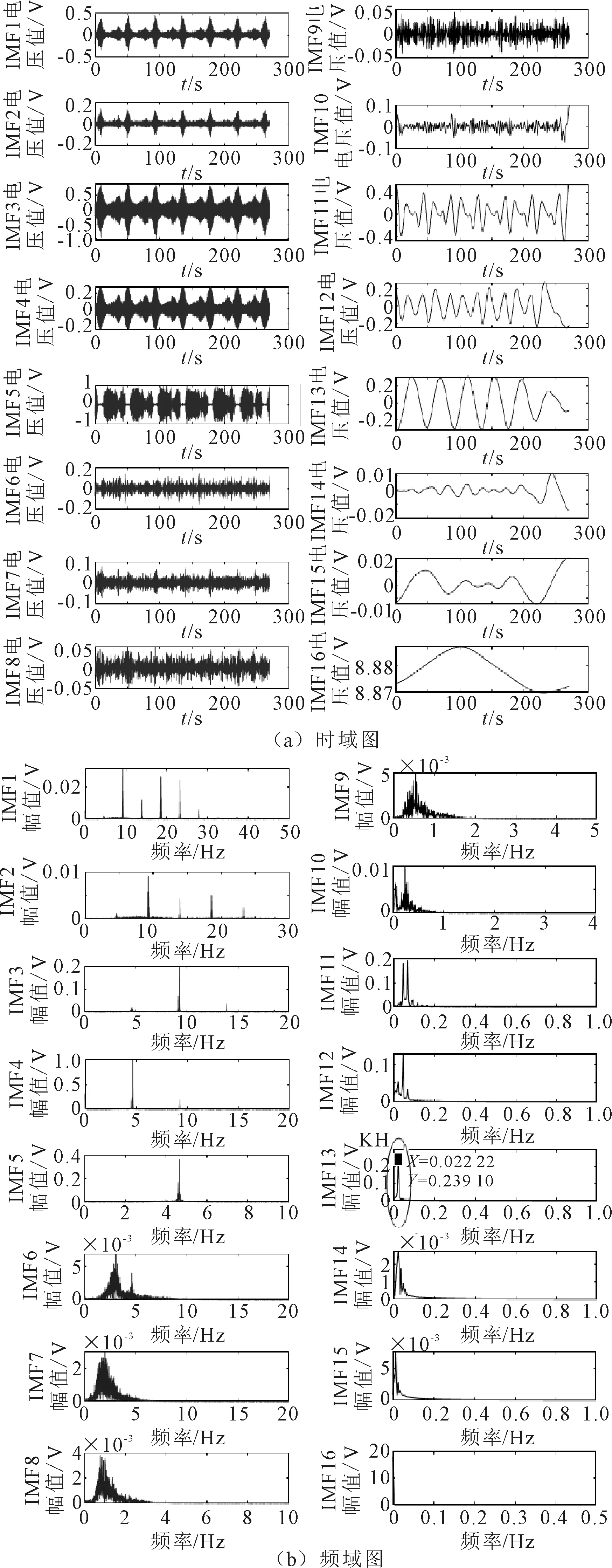
图4 实际信号x6(t)的CEEMD结果

从图2(a)可知，对原始信号进行EMD处理后各阶IMF中并没有较为明显的谐波成分；从2(b)可知，虽然在IMF11中存在频率与筒体工频(0.222 2 Hz)一致的信号成分，但是IMF11中也包含有其他频率的信号成分，这说明对于实际信号x6(t)，EMD方法导致的模式混叠问题较为严重，无法准确提取出KH。由图3可知，在时域上，对x6(t)进行EEMD分解之后的IMF中包含有谐波成分，位于IMF10；在频域上，IMF10的频率为0.222 2 Hz，与筒体工频一致，说明IMF10就是KH，通过EEMD方法能够准确提取出实际信号x6(t)当中的KH成分。由图4可知，在时域上，对x6(t)进行CEEMD分解之后的IMF中包含有谐波成分，位于IMF13；在频域上，IMF13的频率为0.222 2 Hz，与筒体工频一致，说明IMF13就是KH，通过CEEMD的方法能够准确提取出实际信号x6(t)当中的KH成分。

为了验证采取CEEMD方法分析处理x6(t)时，能够有效抑制白噪声产生的影响，比对了EEMD和CEEMD两种信号处理方法对同一信号x6(t)产生的重构误差。图5为EEMD方法的重构误差时频图，图6为CEEMD方法的重构误差图。

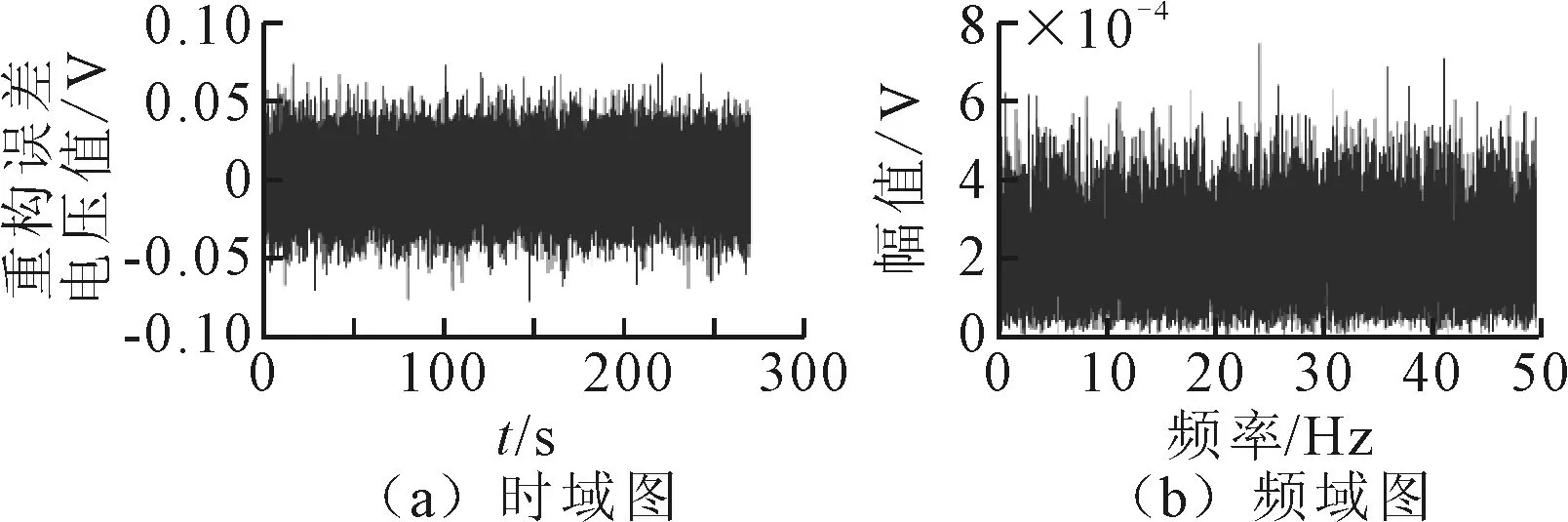
图5 EEMD的重构误差

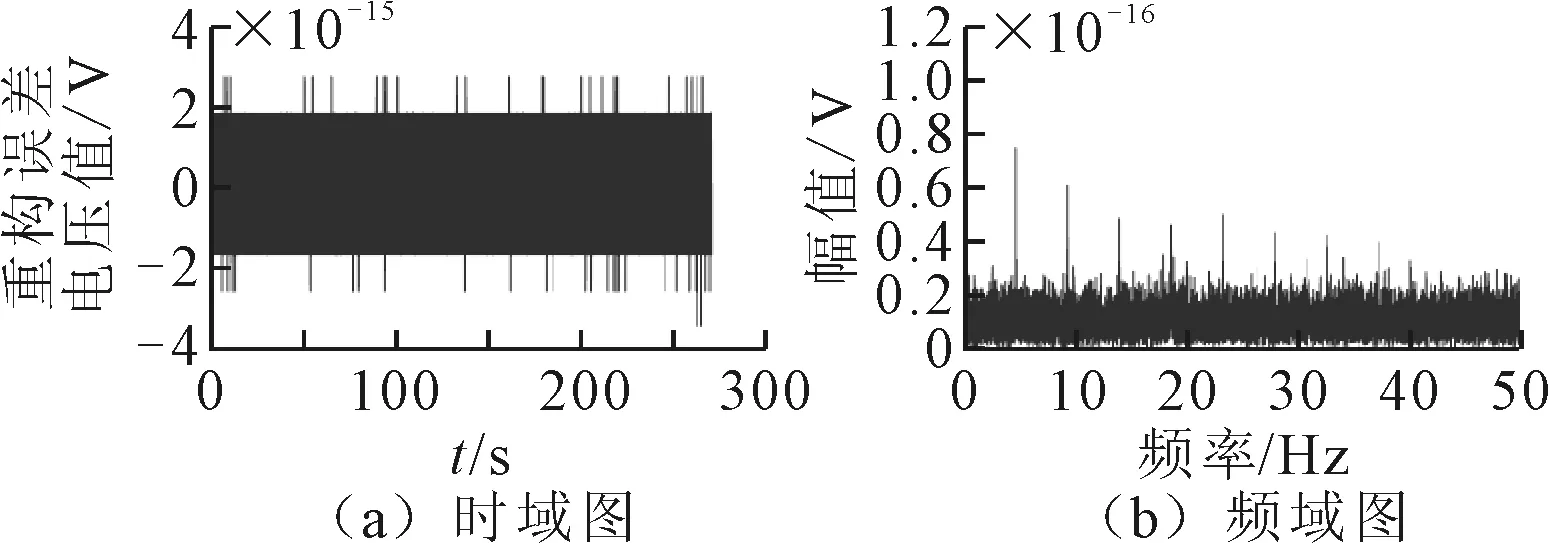
图6 CEEMD的重构误差

对比图5和图6可知：EEMD的重构误差数量级为10-4；CEEMD重构误差数量级为10-16，远低于EEMD的重构误差。说明相比于EEMD，CEEMD能够有效地抑制残余噪声的产生，提高了分解精度，并可以完美重构原始信号。

由上述分析可以得出结论:实际信号x6(t)中存在KH成分；CEEMD相比于EMD能够解决模式混叠问题，CEEMD相比于EEMD能够抑制残余噪声的产生，因此，CEEMD在提取特征谐波KH上效果更好。

3 特征谐波KH与筒体热弯曲故障之间的关系

测量分析某铝厂二号窑大齿圈，该窑大齿圈处存在筒体热弯曲故障，在调整过程中，按照时间先后采集了6组齿顶径向位移信号，其中第一组表示调整前的信号x1(t)，第六组表示调整后的信号x6(t)，通过CEEMD方法提取出各组信号中的KH，并统计了调整过程中KH的幅值a的变化，如表1所示。

表1 调整过程中KH幅值a变化统计

调整前现场采集的齿顶径向位移信号x1(t)在CEEMD下的KH时频图如图7所示。图8为调整后现场采集的齿顶径向位移信号x6(t)在CEEMD下的KH时频图。观察图7(b)和图8(b)可以看出经过调整维护后，KH幅值从调整前的0.309 0缩小为调整后的0.239 1。

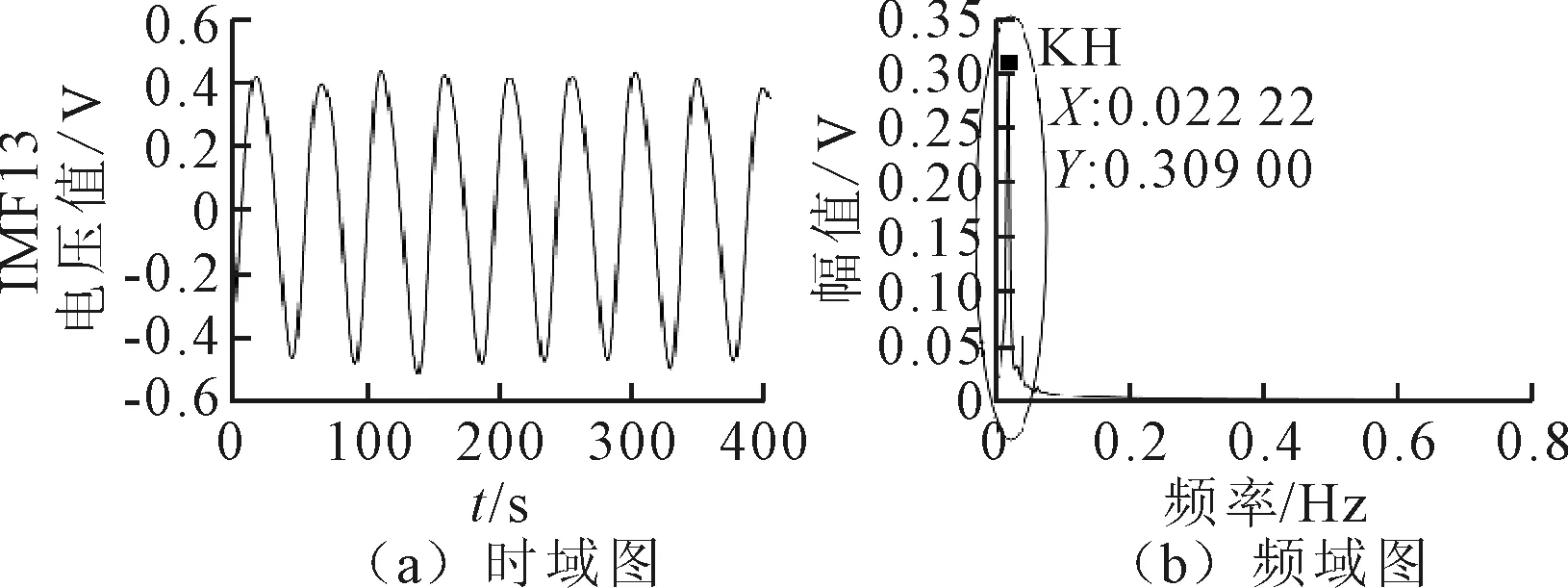
图7 调整前原始信号x1(t)在CEEMD下的KH时频图

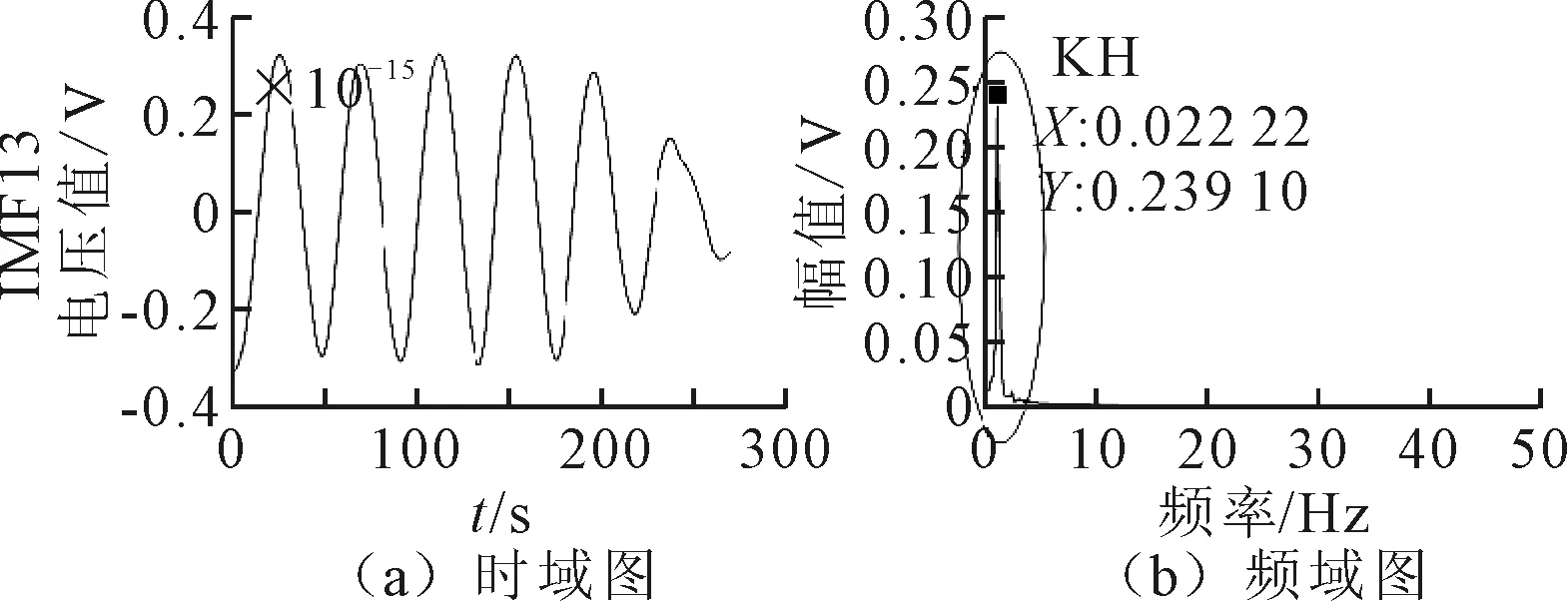
图8 调整后原始信号x6(t)在CEEMD下的KH时频图

为了确定KH与筒体热弯曲故障之间的关系，以筒体偏心距e作为筒体热弯曲的评估参数，通过激光测距法采集筒体表面径向变形数据，利用最小二乘法拟合得到筒体的偏心距值。在调整维护过程中，与大齿圈径向位移信号的采集时间同步地采集了6组筒体表面径向变形数据，拟合得到筒体偏心值e的变化，如表2所示，其中第1组为调整前的数据，第6组为调整后的数据。

表2 调整过程中筒体偏心值e的变化

图9为调整前后筒体截面偏心e的测量结果，观察9(a)和图9(b)，可以看出经过调整维护后，大齿圈附近筒体的截面偏心值e从3.76 mm减小到2.48 mm。

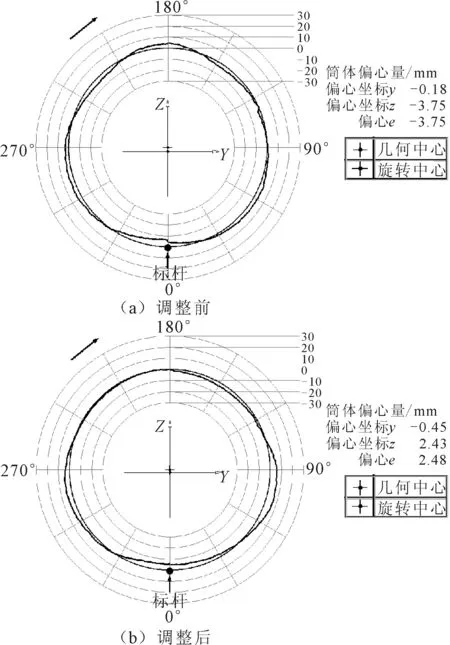
图9 调整前后筒体截面偏心e的测量结果

根据表1和表2可以得到现场KH幅值a与筒体偏心e的关系如图10所示。

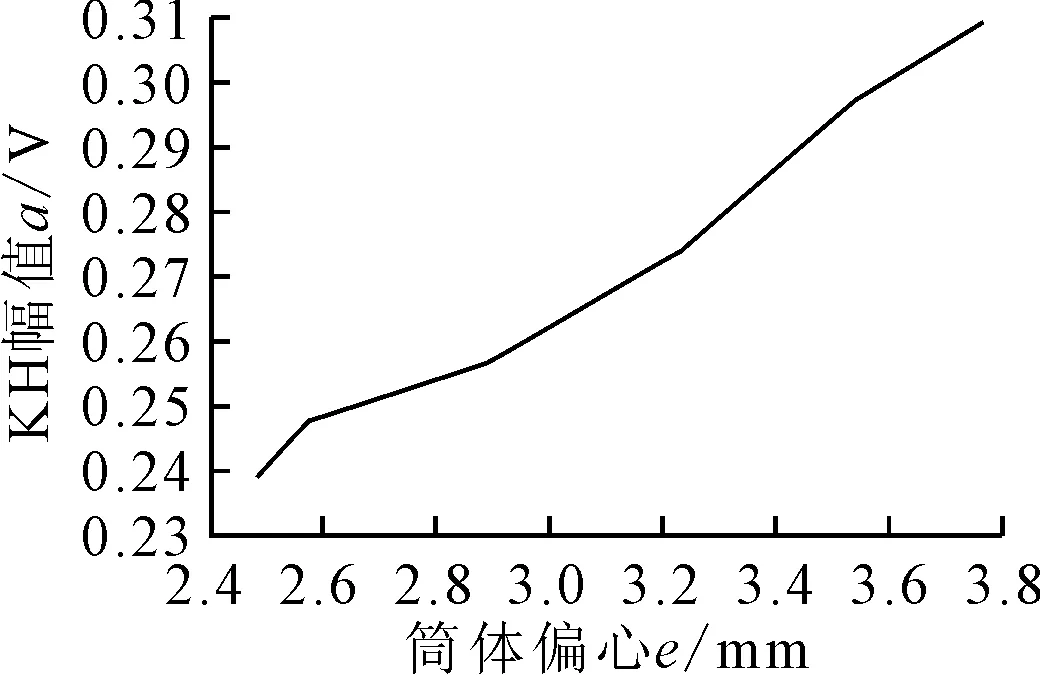
图10 现场KH幅值a与筒体偏心e的关系图

由图10可知，在实际现场中，大齿圈径向位移信号中与筒体工作频率一致的谐波成分(KH)的幅值与筒体热弯曲的评估参数e之间存在正相关关系。说明特征谐波KH包含了回转窑筒体热弯曲故障信息，KH幅值可以作为回转窑筒体热弯曲的检测参数。

4 结论

笔者首先介绍了CEEMD方法理论，通过工程实例对比分析，发现相比于EMD和EEMD，CEEMD对大齿圈径向位移信号的特征谐波KH提取效果更好。以CEEMD方法为基础，统计回转窑调整过程中KH的幅值变化，以传统的激光测距法为基础，同步统计调整过程中筒体偏心距的变化，对比两者的结果，发现特征谐波KH的幅值与筒体偏心距之间存在正相关关系。说明KH幅值可以作为筒体热弯曲故障的检测参数，验证了CEEMD在回转窑大齿圈径向位移信号分析的正确性，为回转窑故障诊断提供了分析依据。