烧蚀磨损对某大口径自行加榴炮动态响应的影响

郭俊行,樵军谋,李宗虎,丁红民

(西北机电工程研究所,陕西 咸阳,712009)

某大口径自行加榴炮初速高、膛压高,因此,身管寿命和射击精度是该型火炮总体关键技术指标,膛线形式成为影响身管寿命和射击精度的关键因素之一。膛线形式的选择,有等齐膛线、渐速膛线、渐速-等齐混合膛线等技术途径。一般认为,采用渐速膛线能够减缓膛线导转侧磨损,改善膛线起始部的受力,而减小这个部位的磨损,有利于提高身管寿命[1-2]。相关研究认为炮口振动是影响射击精度的重要因素之一,反后坐装置布置对动力学响应有一定影响。文献[3]通过对摇架变形及其与反后坐装置相互作用的分析,研究了反后坐装置在摇架上不同安装方式对重复工作一致性的影响,但是仅为定性分析、没有定量计算。文献[4]应用非线性有限元理论,建立了某大口径火炮的发射动力学模型,考虑了机构之间的接触碰撞关系,采用数值计算研究了复进机和驻退机的不同固定方式和不同布置位置对载荷传递规律和炮口振动的影响。文献[5]建立了全炮刚柔耦合发射动力学模型,研究了反后坐装置布局对炮口振动的影响。但是,以上研究并没有考虑弹丸运动。以上研究及相关工程实践均表明,反后坐装置布置对动力学响应有一定影响,采用反后坐装置对射击平面对称布置的方案能够减小对发射系统的影响从而改善射击精度。文献[6]基于SPH-FEM方法建立了全炮发射动力学模型,通过对比仿真结果和试验数据验证了该模型的有效性,研究了弹丸不平衡因素及装填姿态等炮口振动的影响。文献[7-8]建立了烧蚀后身管的动力学模型,研究了烧蚀磨损对挤进的影响。以上研究没有考虑烧蚀等因素对火炮系统振动的影响,该研究仍然有待深入。

本文以采用反后坐装置全对称布置、混合膛线的某大口径自行加榴炮为例,研究烧蚀磨损对其动力学响应的影响;采用有限元理论建立发射动力学模型,研究了内膛不同磨损程度对火炮动态响应的影响,为未来发展高精度、长寿命大口径火炮提供理论参考。

图1 反后坐装置及定向栓布置方案

1 火炮结构及有限元模型

1.1 火炮起落部分结构

该自行火炮反后坐装置及定向栓布置方案见图1。如图1所示,复进机、制退机、定向栓关于火炮轴线对角对称布置。起落部分采用实体单元和壳体单元为主的网格划分方法[9],建立有限元网格,如图2所示。

图2 自行火炮起落部分有限元模型

1.2 烧蚀身管有限元模型

经过一定射击次数后,身管烧蚀明显。图3是某大口径火炮身管实测的阴线、阳线的扩大系数随位置变化图,图中,阳线、阴线扩大系数分别定义为

(1)

(2)

式中:dl为阳线原始直径,d′l为烧蚀后阳线直径;dg为阴线原始直径,d′g为烧蚀后阴线直径;z为测量位置距膛线起始点的距离。由图可见,经过一定射击次数的身管,阴线、阳线的扩大倍数在沿身管长度方向是不同的,在膛线起始段烧蚀明显,而炮口附近烧蚀较小。图3是某火炮实际测径数据,由图可见,膛线起始部向前25.4 mm处阳线直径扩大量为2.1 mm。

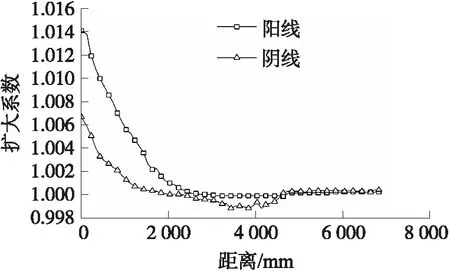
图3 某大口径火炮身管内膛直径烧蚀情况

本文提出了一种烧蚀身管有限元模型建模方法。首先,使用UG软件建立几何母模型,如图4(a)所示,准确建立其坡膛的几何尺寸,简化了膛线横截面上的圆角,膛线部分为拉伸特征。其次,使用HyperMesh等软件对其进行网格划分,得到图4(b)所示有限元母模型。再编程实现坐标径向放大、旋转变换,得到混合膛线身管烧蚀后的有限元网格,见图4(c)。对某样炮进行310发和581发射击,获得实际测径数据,其膛线起始部向前25.4 mm处直径分别扩大了2.1 mm和4.6 mm,经过统计射击数据,分别对应射弹当量数(EFC)240和540。依据膛线部分实测尺寸建立了2个烧蚀身管有限元模型,其膛线部分尺寸均有不同程度的磨损,以下简称“直径扩大2.1 mm”和“直径扩大4.6 mm”。

图4 烧蚀身管建模方法

弹丸网格模型见图5,弹带部分采用光滑粒子单元加实体单元建模[10-13],该方法能够应用于大口径火炮弹丸运动及炮口振动分析[6]。

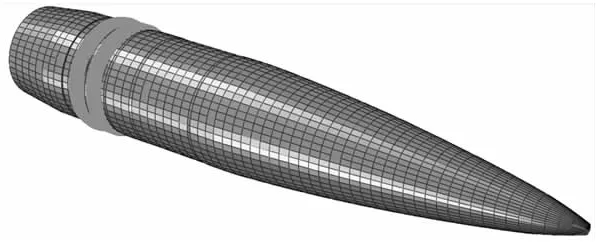
图5 弹丸网格模型

1.3 坐标系

取炮口方向为z轴正向,从炮尾看过去向左为x轴正向,向上为y轴正向。炮口用炮口制退器前端面中心来代替,射击过程中该中心点偏离原始位置,即炮口响应。由于该端面本身基本不变形,它的运动仅仅为平移和端面外法线的转动,即由平动位移和旋转角位移构成。约定炮口在x向和y向的位移为s1和s2,s1向左为正,s2向上为正;绕x轴和y轴转动的角度为α1和α2,即高低和方向角位移,α1向下为正,α2向左为正;具体见图6。

图6 炮口振动位移和角位移方向示意图

1.4 弹炮耦合动力学模型

根据火炮结构的特点,摇架与后坐部分之间通过衬套支撑,同时有定向栓限制后坐部分的旋转,故定义摇架前后铜衬套内表面与身管圆柱部外表面、定向栓室表面和定向栓之间的接触关系。火炮在静止状态下受重力作用产生自重变形,是发射时的初始几何构型。首先,建立静态分析步求解其变形和应力,再导入静态分析结果进行下一步分析。图7是起落部分在0°射角时的静力变形求解结果,从云图可以看出,最大位移为11.48 mm,位于炮口制退器。

图7 起落部分在0°射角时的自重变形

为对比烧蚀对动态响应的影响,分别建立有限元模型。计算条件选为常温全装药,内弹道计算出的压力曲线见图8。弹丸定心部直径取为下偏差,弹丸无质量偏心,高低射角和方向射角取0°。

图8 某装药条件压力曲线

在有限元模型中,在炮尾和摇架之间建立非线性弹簧和非线性阻尼单元,分别用来模拟复进机和制退机。经典内弹道理论认为,随着弹丸行程的增大,弹后空间分布的燃气压力随时间和空间变化,动态地作用在部分身管内膛表面上。根据经典内弹道理论,假设弹后空间的压力分布是一个二次曲线,可以通过膛底压力、弹底压力、弹丸位置,依据公式计算得到。由于在前处理中很难将弹后空间的燃气压力动态地加载到内膛表面,为此本研究对Abaqus/Explicit提供的VDLOAD子程序进行二次开发,以实现压力动态加载,程序流程如图9所示。首先,依据分析步时间,由弹丸行程、后坐行程曲线查表得出弹丸、膛底所处的位置,即可判断内膛表面上某点处于弹前空间还是弹后空间;如果该点处于弹前空间,压力载荷为0;如果是弹后空间,从内弹道曲线上插值得出膛底压力、弹底压力,再依据压力分布插值得到压力载荷。

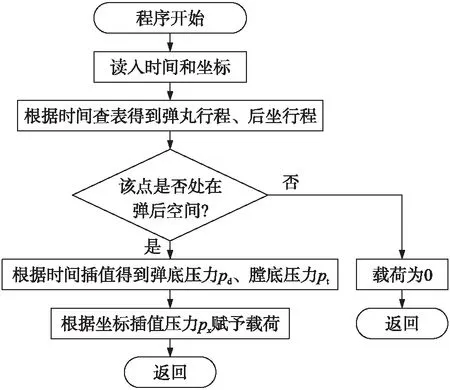
图9 使用VDLOAD子程序实现布尔顿力加载的程序流程图

弹丸在膛内运动时弹带和内膛表面接触,定心部也可能与内膛表面接触,定义定心部表面、弹带和内膛的接触关系;后坐部分支撑在摇架的衬套上,身管外表面和衬套接触,定义身管外表面和衬套的接触关系。

2 计算结果及讨论

2.1 内弹道符合计算

图10是有限元模型计算得到的弹丸加速度a曲线。从图中可以看出,所建立的动力学有限元模型计算出的弹丸加速度与内弹道计算结果符合良好。

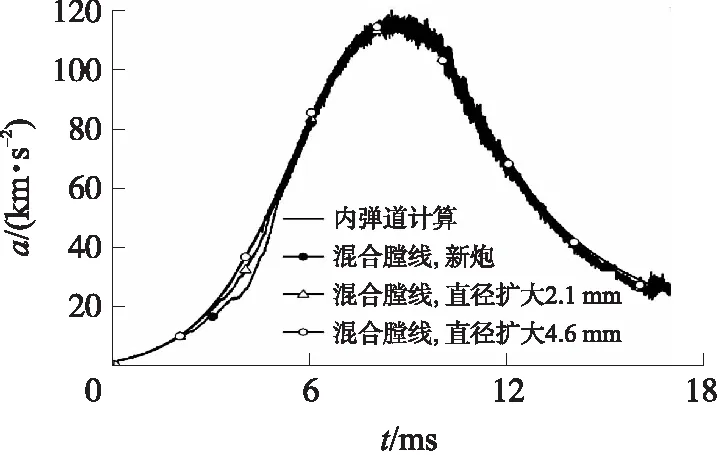
图10 模型计算得到的弹丸加速度曲线

下文图中均采用混合膛线条件。

图11是有限元模型计算得到的弹丸导转力矩M随时间t和弹丸行程l变化曲线。从图中可以看出,所建立的动力学有限元模型计算出的弹丸导转力矩与内弹道计算结果[1]符合良好。

图11 有限元计算得到的导转力矩随时间和弹丸行程变化曲线

2.2 弹丸前定心部力

图12是有限元模型计算得到的弹丸前定心部受x方向接触力Fx、y方向接触力Fy变化曲线。

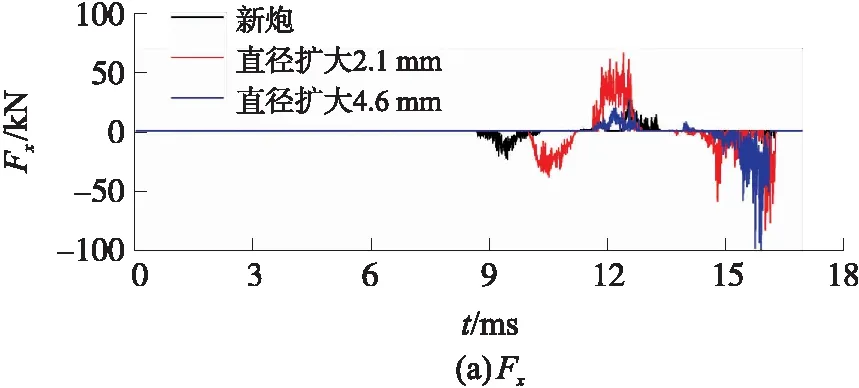
图12 有限元计算得到的弹丸前定心部力变化曲线

从图12中可以看出,在新炮时定心部力持续的时间很短,弹丸在运动时与内膛碰撞然后弹回。在烧蚀磨损后,定心部力持续的时间逐渐增长,定心部力逐渐增大。

2.3 炮口振动响应

图13、图14是有限元模型计算得到的炮口振动响应曲线,图中,s1为左右位移,s2为高低位移,α1为左右角位移,α2为高低角位移,v1为左右速度,v2为高低速度,ω1为左右角速度,ω2为高低角速度。

图13 仿真得到的炮口振动位移及角位移曲线

图14 仿真得到的炮口振动速度及角速度曲线

从图13、图14中可以看出,随着烧蚀磨损量增加,炮口振动位移增加不明显,炮口振动速度有所增大。炮口点左右线速度和角速度有增大趋势,而高低线速度和角速度增加不明显,这与火炮炮口振动产生的机理有关。以后坐部分为研究对象,发射过程中主要外力有反后坐装置力、惯性力、布尔顿力、弹丸作用力等[6]。由于采用了反后坐装置沿火炮轴线对称布置方案,反后坐装置力对炮膛轴线力矩有互相抵消的趋势。惯性力和布尔顿力总是引起火炮在高低方向的振动,其影响反映在高低位移曲线上。身管受弹丸作用力与很多因素有关,前定心部力会受到弹炮间隙影响,有一定的随机性,引起炮口振动的随机性。文献[6]研究结果表明,炮口振动受弹丸与内膛作用影响明显。从图12中可以看出,在采用混合膛线时弹丸转速逐渐增加,弹丸接触力随弹丸行程增加;由图14可以看到,随着内膛磨损量增加,炮口振动速度逐渐增大。

3 结论

本文研究了内膛烧蚀磨损对某大口径自行加榴炮动态响应的影响。采用有限元方法建立了起落部分的有限元模型;依据内膛直径实测数据,建立了2种烧蚀磨损程度的身管模型;仿真了膛内时期起落部分的动态响应,得到了弹丸运动加速度、导转力矩、前定心部力和炮口点振动。经过仿真分析可知,该大口径自行加榴炮采用混合膛线时随着烧蚀磨损增大,弹丸的定心部力逐渐增大,炮口振动位移增加不明显,炮口振动速度有所增大。