基于激光跟踪测量系统的瞄准方法
李文杰,徐 捷,王 新,穆宝忠
(同济大学 物理科学与工程学院,上海 200092)
引 言
激光惯性约束聚变(LICF)是实现受控核聚变的一种方法。在LICF实验过程中会辐射出大量关于空间、时间和能谱分布的等离子体X射线,对这些等离子体X射线进行成像诊断是LICF的一个重要研究领域[1]。LICF物理实验过程的空间尺度仅有几十至几百微米的数量级,以X射线显微镜为例,其有效成像区域仅有几十至几百微米的范围,因此需要高精度定位系统对诊断成像设备进行精确定位[2]。
激光跟踪测量系统基于激光干涉测距原理,具有测量精度高、测量范围大等优点,多路激光跟踪测量系统还可以利用冗余技术实现测量基站空间位置的自标定[3]。因此,激光跟踪测量系统可以对ICF实验中的诊断设备进行精确定位并实现ICF实验靶球的位置标定。激光跟踪测量系统是一种柔性测量系统,可以建立适当的虚拟坐标系,对实验环境要求低,且可以实现快速定位。以FARO ION激光跟踪仪为例,其干涉测量精度(IFM)可以达到 2 μm+0.4 μm/m,绝对距离测量精度可以达到 8 μm+0.4 μm/m[4]。目前,世界上许多高能粒子加速器都采用了激光跟踪仪和其他测量设备的结合进行测量和准直。瑞士光源控制网主要测量仪器为徕卡LTD500激光跟踪仪和N3光学水准仪,测量得到的标准偏差可以达到0.1 mm[5];上海光源控制网利用激光跟踪仪进行准直测量的定位精度达到了0.08 mm[6]。
本文结合LICF实验应用场景,分析了激光跟踪测量系统的分类、原理和组成部分,开展了基于四路激光跟踪测量系统的瞄准方法研究。建立了面向ICF实验过程的自标定和测量模型,并利用最小二乘法中的列文伯格-马夸尔特算法进行了一系列理论计算,最后得到了LICF实验场景下,利用四路激光跟踪测量系统可以实现的理论测量精度。本文为将来在我国激光惯性约束聚变装置上使用激光跟踪测量系统作为瞄准定位设备建立了初步的理论模型并提供了理论指导。
1 激光跟踪测量系统基本概念
1.1 激光跟踪仪测量原理
激光跟踪仪一般由激光干涉测长系统、跟踪控制系统、角度测量系统、目标反射器等组成。其中,跟踪控制系统包括位置探测器(PSD)和跟踪转镜等,目标反射器一般固定在测量物体上,主要有猫眼逆反射器、角锥棱镜等[7]。
激光跟踪仪的测量原理如图1所示。激光跟踪仪可以看成是在激光干涉仪的基础上,增加了可以随被测物体运动而实现自动跟踪测量的跟踪转镜。激光干涉仪可以测量被测物体与测量基站之间的相对距离变化。跟踪转镜由控制电路、PSD和伺服电机等进行控制,经由固定在被测物体上的目标反射器反射回来的激光到达PSD,当物体运动时,PSD上的光斑位置发生变化,控制电路将这一信号反馈给伺服电机,跟踪转镜会发生相应的转动(转动的角度即为物体的俯仰角和偏摆角),对物体进行实时、动态的跟踪测量。
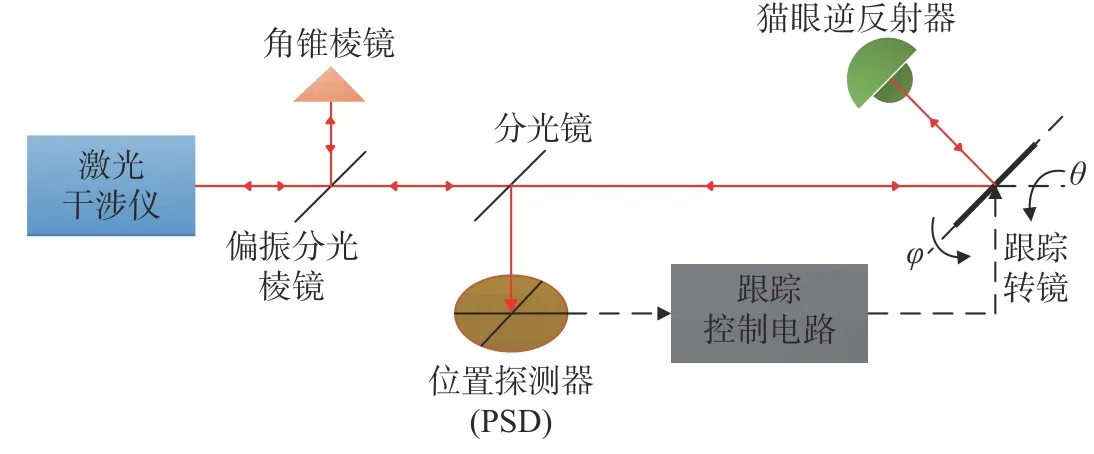
图 1 激光跟踪仪测量原理图Fig. 1 Representation of laser tracker measurement principle
1.2 四路激光跟踪测量系统
根据测量基站的数量和测量原理,激光跟踪测量系统可以分为单站球坐标法、双站三角法和多路多边法激光跟踪测量系统。其中,单站球坐标法和双站三角法激光跟踪测量系统的测量误差包括测长和测角误差,并且测角误差会随着测量距离的增大而增大,因此测量精度相对较低。多路多边法激光跟踪测量系统的测量误差只包含测长误差,理论上精度最高[8]。
在直角坐标系中,1个目标点只需3台激光跟踪仪作为测量基站即可确定其空间所在位置(x,y,z)。每一个测量基站可以测出被测目标点到各个基站的相对距离变化量,当3个测量基站在直角坐标系中的位置关系被确定后,被测目标点的空间位置即可被精确测量,因此在测量前需要对每个基站进行空间位置标定。
图2所示为四路激光跟踪测量系统示意图,图中Bi(i=1,2,3,4)为4个测量基站,Ti为目标反射器,安装在待测物体上。四路激光跟踪测量系统一个最重要的特性就是可以利用冗余技术对4个测量基站的空间位置进行自我标定,无需借助外界标准测量器件即可确定测量基站的空间位置,极大地提高了测量效率,缩短了在LICF场景下诊断实验设备的瞄准定位时间,并且不使用角度量,只使用长度量测定待测目标物的空间位置,理论上具有很高的测量精度。此系统的测量误差主要取决于系统自标定过程产生的误差和单台激光跟踪仪自身的测量误差,因此本文采用四路激光跟踪测量系统作为面向LICF过程的瞄准测量设备[9]。
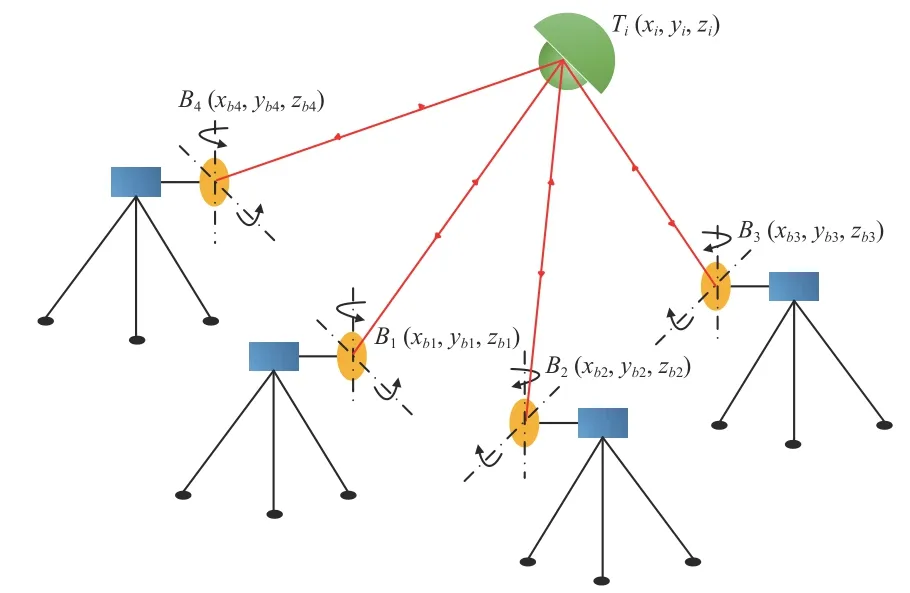
图 2 四路激光跟踪测量系统Fig. 2 Four-beam laser tracking measurement system
2 面向 LICF 过程自标定模型的建立和理论计算
2.1 模型的建立
四路激光跟踪测量系统可以实现4个测量基站空间位置的自标定,对于每一个被测目标点Ti,可以分别与4个测量基站Bi(i=1,2,3,4),根据两点距离公式建立4个方程。每一个待测目标点Ti只需要其中3个方程就可以确定它的空间位置,因而存在1个冗余约束方程。因此,可以采用信息冗余的方式,通过增加动点的数目,使冗余约束方程的个数大于四路激光跟踪测量系统未知参数的个数,即可实现四路激光跟踪测量系统的未知参数自我标定,这就是系统自标定的原理[10]。
系统自标定的目的是通过组成四路激光跟踪测量系统的4个基站跟踪同一个目标反射器,目标反射器安装在被测动点上,进而可以得到每个动点到4个测量基站的相对长度变化量,从而确定系统的未知参数。系统的未知参数包含4个测量基站的坐标和1个初始动点的坐标,共15个。如图3所示,建立合理的虚拟坐标系可以减少系统的未知参数个数,减少工作量和时间。以其中1个测量基点B1为坐标原点,基点B2位于x轴上,基点B3位于XB1Y平面内,根据右手螺旋定则建立图3所示空间直角坐标系。此时系统未知参数分量中有6个坐标分量均为0,因此系统的未知参数可以从15个减少至9个。4个测量基点和1个初始动点的坐标可以记为:B1(0,0,0),B2(xb2,0,0) ,B3(xb3,yb3,0) ,B4(xb4,yb4,zb4),Ti(xi,yi,zi) , 其 中Ti(i=0,1,···,n) 表示空间某一运动点的位置,定义i=0 时即T0(x0,y0,z0)为初始动点[11]。

图 3 虚拟坐标系Fig. 3 Virtual coordinate system
将系统的未知参数定义为向量s=[xb2,xb3,yb3,xb4,yb4,zb4,x0,y0,z0],假设待测动点数目为n,每个待测动点与4个测量基点之间按照距离公式可以建立4个方程,n个动点则可以建立4 ×n个约束方程,同时也会引入3 ×n个未知量,加上9个系统未知参数,共 3 ×n+9 个未知量[10]。为确定系统参数未知量的值,必须满足
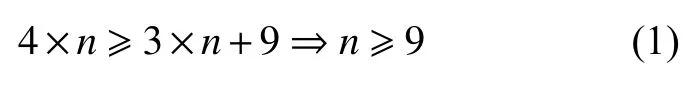
从式(1)可以看出,对于四路激光跟踪测量系统,要实现系统在测量前的测量基站自标定任务,选取的待测动点数目必须大于等于9个。
如图3所示,初始动点T0到4个基点的距离定义为初始长度,记为Lj(j=1,2,3,4) 。4个测量基站跟踪测量同一目标反射器,可以测量出每个动点到4个测量基站的相对长度变化量。当4个测量基站瞄准初始动点时,4个激光跟踪仪测量基站的读数均设置为0,那么在待测物体也即目标反射器移动过程中,激光跟踪仪的读数就是待测动点到测量基点的相对长度变化量,记动点Ti到Bj的相对长度变化量为lij(i=1,2,···,n)[10]。
对于三维空间中的任一动点Ti(xi,yi,zi) ,每个动点和4个基点间,根据两点距离公式可以建立如下方程组:
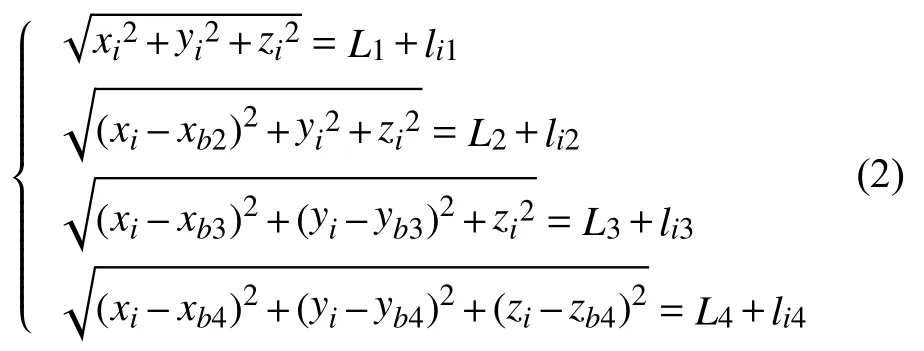
式(2)中,i=1,2,···,n,n为动点数。Li的值可以由式(3)给出,式(3)中 (x0,y0,z0) 为初始动点T0坐标。
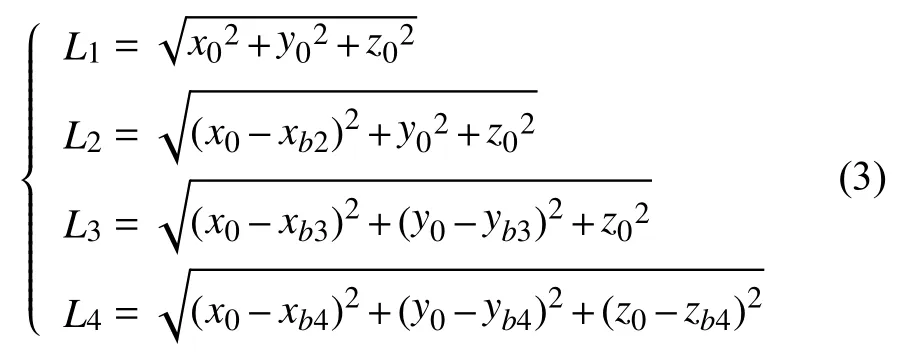
四路激光跟踪测量系统的自标定过程实际上可以视作一个无约束最优化问题,可以采用相应的无约束最优化数值解法进行自标定过程的求解。由于系统测量过程的精度受系统自标定过程精度的制约,因此必须提高系统的自标定精度。在自标定过程中,四路激光跟踪测量系统动点数目应该大于9个,以此达到提高系统自标定精度的目的,此时会构成超定方程组。为求得超定方程组的最小二乘解,往往将其转化为与之等价的无约束最优化问题,然后采用数值优化算法,如信赖域法、高斯-牛顿法、广义逆法、列文伯格-马夸尔特算法等进行求解[10]。此时需要给出评价函数J,其表达式为
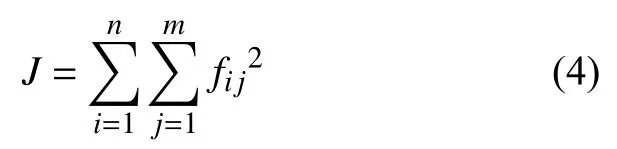
式中fij为残差表达式。最优化问题是选取合理的系统未知参数使评价函数J最小。以系统未知参数和所有动点坐标作为未知量,残差表达式定义为动点到每个基点的距离变化量与实际测量值之差,即

式中:i=1,2,···,n;j=1,2,3,4 。
2.2 理论计算
基于上述四路激光跟踪测量系统的自标定数学模型,进行了一系列理论计算,模拟LICF实验环境下的自标定和测量过程,理论计算包含了整个自标定和测量过程的仿真模拟。事先给定系统未知参数的真值,并且在10 000 mm×10 000 mm×10 000 mm区域内产生若干个动点,由上述数据可以计算出每个动点到4个基点的相对长度变化量lij,最后采用列文伯格-马夸尔特算法进行求解[11],通过这些数据可以反向求出系统未知参数的迭代终值。系统未知参数的真值如表1所示。
列文伯格-马夸尔特算法流程如图4所示。
基于上述数学模型和数值算法,通过理论计算中的自标定部分,进行了以下两种情况下的仿真模拟。
(1)假设激光跟踪仪不存在测量误差,即不需要给测量基点和动点之间的相对长度变化量lij加上服从正态分布的误差。给定与系统未知参数真值3种不同偏差情况下的未知参数初值,如表2所示,这种情况下的理论仿真是为了考察采用的数值优化算法是否对初值敏感。在10 000 mm×10 000 mm×10 000 mm区域内按随机分布产生140个动点,并在3种不同初值情况下进行理论计算,求出不同初值情况下的未知参数迭代终值与真值的最大偏差的绝对值和评价函数J的值,所得仿真结果如表3所示。

表 1 系统未知参数真值Tab. 1 Designed values of the unknown parameters of the measurement system

图 4 列文伯格−马夸尔特算法流程图Fig. 4 Flow chart of Levenberg-Marquardt algorithm
由表3可以得出结论,对于不同偏差情况下的初值,最终得到的迭代终值与真值的偏差绝对值都非常小,说明选用的自标定数值优化算法对初值不敏感,计算结果都非常接近真值,因此所选用的列文伯格-马夸尔特算法是在LICF实验场景下求解测量系统未知参数的最小二乘解的优良算法。
(2)激光跟踪仪存在测量误差,测量误差为10 μm,也即需要给相对长度变化量lij加上一个均值为0 μm、标准差为10 μm的正态分布。在10 000 mm×10 000 mm×10 000 mm区域内按随机分布分别产生140个动点、120个动点、100个动点、80个动点、60个动点、40个动点和20个动点,选择第(1)种仿真情况下的偏差1系统未知参数迭代初值,在不同点数情况下进行理论仿真,最终得到的迭代终值与系统参数真值的偏差绝对值以及不同动点数情况下的系统未知参数标准差,结果如图5和图6所示。
图5为不同点数情况下,理论仿真得到的系统未知参数迭代终值与真值偏差的绝对值的柱状图。横轴代表系统未知参数,纵轴代表理论计算得到的系统未知参数均值与真值偏差绝对值的大小。

表 2 不同偏差情况下的系统未知参数迭代初值Tab. 2 Initial iteration values of the unknown parameters with different deviations

表 3 激光跟踪仪没有测量误差时在不同初值情况下的仿真结果Tab. 3 Simulation results of different initial values as the laser tracker is without measurement error

图 5 不同点数情况下,理论仿真得到的位置参数迭代终值与真值的偏差绝对值Fig. 5 The absolute value of the deviation between the iteration value of unknown parameters obtained by theoretical simulation and the truth value at different points
图6为不同点数情况下,理论仿真得到的迭代终值的标准差的柱状图。横坐标代表系统未知参数,纵轴代表理论计算得到的迭代终值标准差大小。
由图5和图6可见,随着选取动点数目的增多,四路激光跟踪测量系统各个未知参数的迭代终值与真值的偏差绝对值和标准差都在减小。因此可以通过增加动点数,采用信息冗余的方式,有效地提高系统未知参数自标定的精度,减小自标定带来的测量误差。

图 6 不同点数情况下,理论仿真得到的终值的标准差Fig. 6 The standard deviation of the final value obtained by theoretical simulation at different points
3 面向 LICF 过程测量模型的建立和理论计算
3.1 模型的建立
在LICF成像诊断实验中,以X射线成像诊断设备为例,诊断设备的像质随视场变化明显,空间分辨率优于5 μm的成像仅在百微米量级,所以视场定位精度要求非常高,必须将ICF物理实验靶放置在诊断成像设备(如X射线显微镜)的光轴上才可以避免X射线成像质量的下降,但在实际情况中,瞄准定位设备总是存在测量误差,ICF实验靶与光轴之间总是存在着偏差,为此提出了面向LICF实验过程的四路激光跟踪测量系统的初步测量定位模型。
由于ICF实验靶丸的尺寸仅在毫米量级,而激光跟踪仪的靶球尺寸为厘米级别,因此采用激光跟踪测量系统对实验靶丸的定位需要借助双光路交汇瞄准系统实现,具体的实验部件排布示意图如图7所示[12]。以选用的四路激光跟踪测量系统中的其中两台激光跟踪测量系统为例,这两台激光跟踪测量系统对靶室中心定位,两个测量基站发出的激光会在靶室中心(ICF靶丸的位置)相交于一点,因此利用DIM(通用诊断操作平台)搭载探测器以及基于可见光辅助瞄准的双光路显微镜,探测器对两个测量基站发出的激光的交点进行探测成像,然后利用双光路显微镜对探测器上激光的交点进行成像并调节双光路显微镜的空间姿态直到在两台双光路显微镜中均可以看到清晰的激光交点为止,此时将探测器取出替换成ICF实验靶丸,根据双光路显微镜中靶丸的清晰程度调节靶丸的空间位置直到在双光路显微镜中能看到靶丸清晰的像即可。由于基于可见光辅助瞄准的这种探测手段精度极高,因此在后面的理论计算中其测量误差忽略不计。

图 7 实验元件排布示意图Fig. 7 Schematic diagram of the arrangement of experimental components
如图8所示,离线状态下,在LICF诊断成像设备(如X射线显微镜)上选取不在同一平面上的3个点A、B、C以及诊断成像设备光轴上的两个点O和P,它们的坐标已知分别为A(100,337,24)、B(52,70,150)、C(149,145,174)、O(5 000,5 000,5 000)、P(1 423,2 642,4 314),利用这 5个点就可以确定诊断成像设备的位置,同时光轴OP和AC的夹角也可以利用向量点乘计算得出,夹角α=80.683 7°,光轴位置也随之确定。实验状态下,选取5个相同的猫眼逆反射器,并将它们放置在选取的上述5个点的位置,光轴上的O点为ICF靶球所在位置,利用四路激光跟踪测量系统测量4个基站到上述5个点的相对距离,则可确定实验状态下的诊断成像设备以及光轴和ICF实验靶的相对位置。

图 8 测量模型的示意图Fig. 8 Diagram of the measurement model
3.2 理论计算
利用理论计算中的自标定部分得到的四路激光跟踪测量系统的4个基点的坐标,进行LICF实验场景下的理论计算。
假设激光跟踪仪的测量误差分别为10 μm和5 μm,即需要将4个基点到选取的5个点的相对长度变化量分别加上1个均值为0 μm、标准差为10 μm的正态分布和1个均值为0 μm、标准差为5 μm的正态分布,进行理论计算得出不同激光跟踪仪测量误差下光轴与LICF成像诊断设备理想光轴之间的夹角误差以及LICF实验靶球与理想光轴的距离偏差的均值,仿真结果如表4所示。
从表4可以看出,对于不同精度的激光跟踪仪,精度越高,最后仿真迭代得到的夹角误差和距离偏差就越小。因此在实际操作中,应该尽可能选用精度更高的激光跟踪仪作为四路激光跟踪测量系统的组成部分。
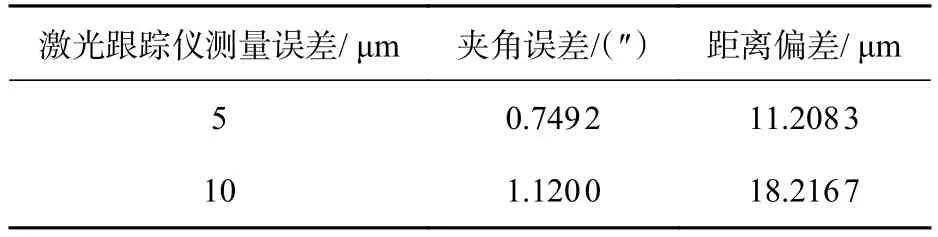
表 4 激光跟踪仪测量误差分别为 10 μm 和5 μm 时的仿真结果Tab. 4 Simulation results of laser tracker with measurement errors of 10 μm and 5 μm, respectively
4 结 论
本文围绕激光惯性约束聚变实验场景,提出了激光跟踪测量系统作为LICF实验诊断设备的瞄准定位装置,建立了LICF诊断设备的初步瞄准定位理论计算模型。利用列文伯格-马夸尔特算法,通过一系列的理论计算,最终得到在激光跟踪仪测量误差为5 μm时,角度误差为0.749 2″,距离偏差为11.208 3 μm;在激光跟踪仪测量误差为10 μm时,角度误差为1.12″,距离偏差为18.216 7 μm。这为将来在我国激光惯性约束聚变装置上使用激光跟踪测量系统作为瞄准定位设备提供了参考。

