插值和拟合方法在高程异常模型建立中的应用

周 伟

（1. 山东省临沂市水利勘测设计院，山东 临沂 276002）

网络RTK技术的发展为采集数据提供了方便，通过流动站GPS的观测可以得到任意位置的平面坐标（如2000国家大地坐标）和大地高。似大地水准面的高程可通过似大地水准面精化的成果获得，也可通过水准测量拟合的方式来获得[1-4]。由于似大地水准面精化的成果一般都是保密的，很难获得，因此利用插值和拟合方法求解高程异常就成为了必须的测量工作。在工程测量工作中，经常采用工地校正或选取几个点解算高程异常的方法，但在覆盖区域较大的情况下（如临沂市沂河及其支流水位的推算），该方法将给工作带来不便。现有的一些GPS自带的处理软件在求解转换参数上会有离散点数量上的约束（如天宝GPS最多为19个点），当点过多时则无法求解，需对项目进行分块求解，但利用不同的项目分块将导致模型的不一致，在后期检查、施工时也将加大工作难度。

为了获取临沂市整个区域的高程异常分布规律，本文介绍了多项式插值曲面、三次样条函数插值曲面（Spline插值）、三次B样条插值曲面以及多项式拟合曲面数学模型[5-8]，并利用临沂市国土局提供的两套共203个平高控制点（1980西安坐标系/2000国家大地坐标系，1985国家高程基准的水准高/大地高，平高同点）计算高程异常；再分别利用插值和拟合模型对高程异常进行求解，分析这些模型与临沂市精化GPS数据的一致性。

1 高程异常模型的计算方法

1.1 插值模型

高程异常插值曲面是对已知高程异常点的插值，得到未知区域的高程异常，本文主要讨论多项式插值曲面和样条函数插值曲面[5-8]模型的数学表示方法。

1.1.1 多项式插值曲面

1）线性插值曲面。该方法比较简单，计算公式为：

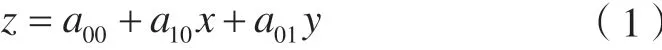
首先构建三角网，并分别对两个方向进行求导，即可得到两个方向的斜率，通过三角网的3个端点值就可求出方程，从而得到三角网内任意点的值。该插值方法是通过已知端点得到的方程，运算速度较快，得到的曲面不光滑，可用来查看高程异常曲面的插值效果。

2）高次多项式插值曲面。对于n＞1的情形，其计算公式为：

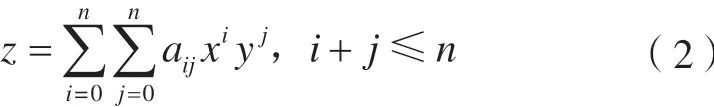
线性插值可表示为n=1的情形；当n=3时，即三次多项式插值就需要求解10个未知数，次数越高，需要求解的未知数就越多。以n=3为例，计算未知数的过程依赖于插值数据的特性，常用方法为利用4个邻近顶点的高度以及每个顶点的3个导数方程，一阶导数分别表示两个方向的表面斜率，二阶导数表示同时在两个方向的斜率，将顶点值代入多项式和导数方程，即可求解出这10个未知数。

1.1.2 三次样条函数插值曲面

1）Spline插值。Spline插值是在多项式分段插值的基础上发展而来的[5]，克服了曲线不光滑，只有一阶导数连续的缺点。三次样条函数的定义为：设则三次样条函数且在每个区间为三次多项式，同时满足三次样条函数的精度依赖于节点的数量，若测量时观测数据较少，则会引入误差。该方法可表述为特定的方法求解各区间的三次多项式。

2）三次B样条插值曲面。B样条曲线是Bezier曲线的进一步发展，也是样条函数的进一步发展。该方法克服了Bezier曲线阶次过高、缺乏灵活性的缺点，可通过反求的方式得到经过各端点并连续的方程[6-7]，目前已被广泛应用于工程制图方面[8]。三次B样条插值曲面模型如式（3）所示，其中0≤t≤1。

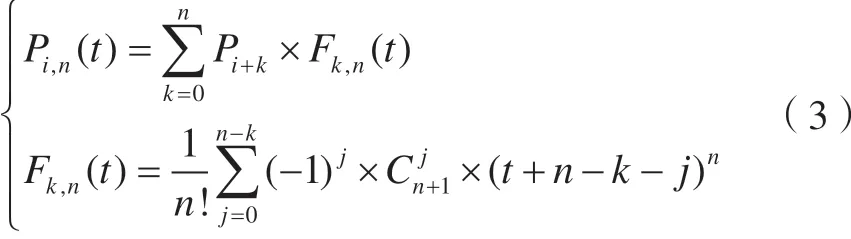
三次B样条是B样条为3次的特殊情况，通过相邻4个顶点即可计算得到三次B样条的曲面形状；当端点多于4个时则可通过反求的方式得到经过各端点并连续的方程，从而得到区间内的插值曲面模型。

1.2 多项式拟合曲面模型

多项式拟合曲面模型如式（2）所示，理想状态下，已知点均通过拟合曲面；但实际上当已知点的数量大于需要求解的未知参数时，总会有节点不通过曲面方程，即存在误差。由于高程异常由两个方向的值确定，即两个自变量确定一个因变量的情况，为了得到区间内最优的曲面方程，就需要利用二元回归的方法寻找一个最接近已知点的曲面，利用最小二乘方法进行约束[5]，使高程异常误差的均方根误差最小，从而求出唯一最优的曲面方程。

2 实验与结果分析

2.1 数据准备

本文采用的数据包括临沂市国土局提供的1980西安坐标系的GPS C级点、II等三角点共203个，其中1985国家高程基准的III等水准点138个、GPS精化高程点65个（平高同点），以及2000国家大地坐标系下这203个平高控制点。高程异常可表示为大地高减去正常高，利用已知数据求解得到203个点的高程异常值，作为精度统计的标准值。在现阶段的测量工作中，推荐使用2000国家大地坐标系，在实验中将2000国家大地坐标作为自变量对高程异常曲面进行插值和拟合。

2.2 数据实验

实验主要利用Matlab 2018b软件进行实现，首先分别利用线性插值、三次多项式插值和三次B样条插值对138个III等水准点进行插值，插值曲面如图1～3所示，并利用插值曲面函数对65个已知的GPS精化高程异常进行计算，得到实际值与模型估算值的误差；再分别利用1～5次多项式拟合方法对138个III等水准点的高程异常曲面进行求解，并利用求解的曲面模型对65个已知的GPS精化高程异常进行计算，得到实际值与模型估算值的误差。多项式拟合曲面如图4～8所示。

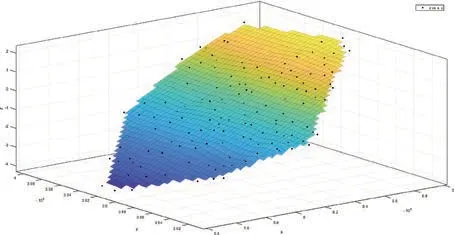
图1 线性插值曲面

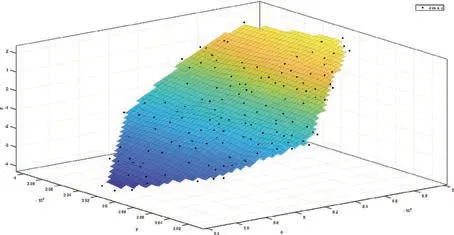
图2 三次多项式插值曲面

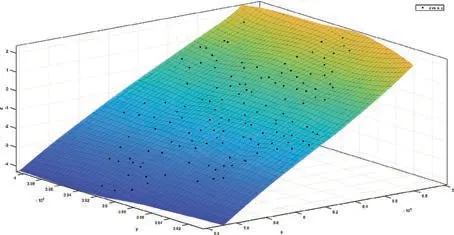
图3 三次B样条插值曲面

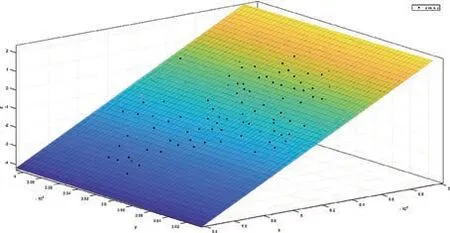
图4 线性拟合曲面

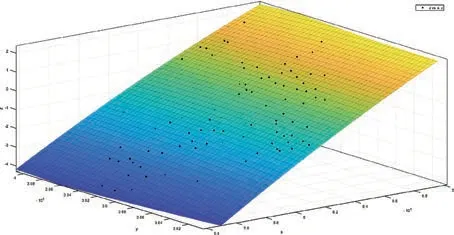
图5 二次多项式拟合曲面

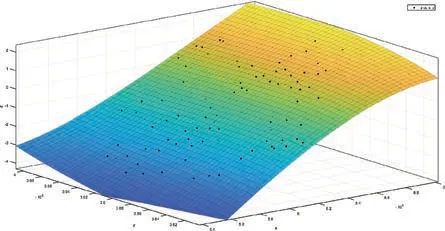
图6 三次多项式拟合曲面

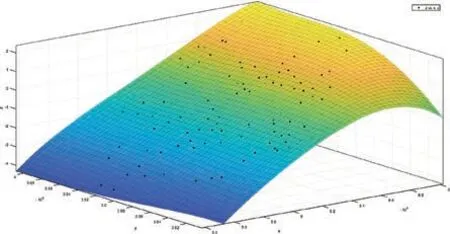
图7 四次多项式拟合曲面

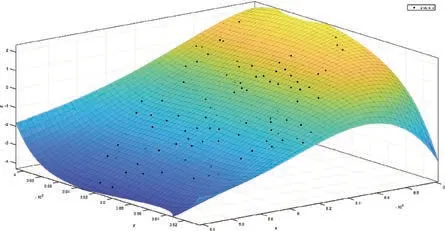
图8 五次多项式拟合曲面

2.3 数据分析

2.3.1 定性分析

1）通过图2、3可直观发现，多项式插值方法只对已知节点进行插值，而样条插值方法和拟合方法，在东坐标和北坐标的区间范围内均可估算高程异常曲面。

2）插值方法可以保证插值曲面经过插值节点，但整体是不光滑的；拟合方法不能保证通过所有节点，但整体是比较光滑的。

3）多项式拟合曲面时，次数大于3时，在没有点控制的边缘区域将产生较大的形变。

2.3.2 定量分析

1）拟合曲面的精度统计。由于插值方法通过插值节点，因此理论上插值曲面的节点误差为零。拟合曲面不能保证所有节点都通过拟合曲面，存在误差，多项式拟合曲面中误差统计如表1所示。多项式拟合模型的高程精度至少可达0.1 m，利用三次多项式拟合时的高程精度为0.06 m。

表1 多项式拟合曲面中误差统计/m

2）检验点的精度统计。本文分别讨论插值曲面和拟合曲面求解65个检验点的精度，由于高次多项式拟合曲面在边缘区域变形较大，且精度提升不明显、多项式系数较多不方便计算，因此这里不再统计3～5次多项式拟合曲面的精度。插值和拟合方法精度统计如表2所示。

3）精度分析。由表1可知，多项式拟合方法可用于评价已知III等水准数据的质量，这里表明国土局提供的水准数据质量还是比较好的，精度优于0.1 m。由表2可知，不同模型得到的精度是不同的，插值曲面的精度低于拟合曲面的精度；插值曲面并不是模型越复杂精度越高，从插值模型的精度统计来看，线性插值曲面精度优于样条插值曲面和三次多项式插值曲面；多项式次数不同拟合曲面的精度也不同，二次拟合曲面精度优于线性拟合曲面精度；从样条插值曲面和拟合曲面的最大残差分布和中误差统计情况来看，曲面的边缘在没有控制点的情况下，精度略低，为了达到更高的精度需适当增加边缘控制；二次多项式拟合曲面与临沂市GPS精化高程的一致性最好，精度最高，检查点中误差为0.038 m，除了插值区域外的一个点，其余点的检验残差均优于0.1 m，高程精度满足1∶500～1∶2 000等大比例尺地形图测量规范要求。

表2 插值和拟合曲面求解高程异常残差统计

3 结 语

插值和拟合曲面模型是求解高程异常的一种方法，不同的区域可选择不同的模型进行高程异常解算。通过实验发现，临沂地区利用多项式拟合曲面模型优于插值曲面模型，插值和拟合精度是否能通过节点的增加而进一步提高，将在下一步的工作中逐步完善。

拟合曲面模型减少了大面积测量时GPS数据处理软件无法控制全区域而将项目分块的麻烦，通过多项式拟合方法得到的模型是唯一最优解，多项式系数是唯一确定的，这样就可以将高程异常的求解转化为平面坐标和高程的函数关系。每次外业作业结束后可通过函数关系将GPS采集的 2000国家大地坐标和大地高转化为2000国家大地坐标和正常高，同时保证了整个临沂市高程异常数据的完整性，为临沂市整个区域范围内的大面积测量提供了方便。