面向新高考“3+X”走班制排课的优先度算法
儒曼,武迪,张致远
(1.北京交通大学 电子信息工程学院,北京 100044;2.清华大学 航天航空学院,北京 100084)
0 引言
“新高考”政策下,高中物理、化学、生物、地理、历史、政治成为选修课,每名学生可任选其中3门作为高考选修课,高考时计入高考总分;其余3门作为会考选修课,只判断是否合格,而不记入高考总分。在这种情况下,学校势必要走班管理,即语文、数学、英语等仍可按照固定班级教学,而选修科目则必须走班教学,以满足每个学生的选择。此时,各个学生选课情况不同,需要针对选课情况给出每名学生的“一人一课表”,在学校有限的教学资源下,排课的组合优化难度大,传统的人工排课不再适用,迫切需要一定优化策略下的智能排课算法。
一般而言,排课问题是一类NP完全问题,涉及多因素的排列组合优化,考虑实际排课需求的约束复杂多变,解空间随学生人数的增加而急剧增大。国内外学者应用了多种不同的算法解决排课问题,如遗传算法[1-2]、蚁群算法[3]、模拟退火算法[4]、整数规划[5]等。这些算法大都应用于传统的教学模式,即只存在固定班的情况。而在高考改革的新形势下,需要将走班制纳入考量范围。与传统的固定班排课不同的是,走班制排课需要制定合理的分班策略。目前采用的分班策略有如下几种:(1)不走班,缩减原有的20种选课方式,仅挑选出几种方案供学生选择。这种策略的优点是排课难度降低,但无法满足学生个性化需求;(2)小走班,如“定两科走一科”;(3)大走班,即本文所采用的模式:选修课应用走班制,固定课应用传统排课方式;(4)全走班,即无固定班。相对第三种策略[6-7],全走班通常需要占用更多的学校教学资源且管理难度更大。
在遗传算法的基础上,针对走班制的分班策略,文献[8]提出了教学班组合的概念,将所有班级分成若干个批次, 每个批次下划分若干个走班组合以简化排课过程;文献[9]从课表时段分配转为天课时分配,即对每个课程班每天的课时数目进行决策;文献[10]采用按选课组合分班,结合遗传算法解决排课问题。上述方法均假设了一定的人为分班策略,限制了解空间的大小,而且对于教学资源的约束情况考虑较少,在资源紧缺的情况下上述排课算法难以生成排课结果。
本文采用大走班的方式,将选修课时和固定课时分开,着眼于选修课时的排课算法。针对学生的选课情况以及学校的教学资源约束,本文排课算法以优先度为指标逐渐构建走班制班级,最终给出一个可行的选修课排课方案。通过设计优先度指标自动生成走班制的动态班级分班结果,无须额外制定分班策略。
1 课时分区处理
针对新高考“3+X”改革实行的走班制排课,本文将所有教学课时分开处理。第一类是固定课课时区。所有学生在这些课时中只上语文、数学、英语、体育、音乐、美术等行政班科目,这一部分与传统的排课相同,可以用固定课排课方法解决;第二类是选修课课时区。所有学生在这些课时中只上物理、化学、生物、地理、历史、政治。此类课时区又细化为两类课时区:1、高考课时区,即学生选考的科目所在课时;2、会考课时区,即学生未选考,将参加会考的科目所在课时。换言之,就是所有学生同一时间的上课科目类型相同。
由于课时分区只是将走班与固定班分开,未改变固定课时总数,因此课时分区不会减少固定班排课的节空间,但这样的课时分法可以把固定课和选修课分开处理,从而简化排课过程。本文即针对其中的选修课时区提出一种能够得到可行解的算法策略。由于高考课时区和会考课时区排课过程相似,以下的数学模型和算法策略部分只讨论高考课时区排课问题。
2 优先度算法
选修课时区的排课问题是:在有限的教师数和教室数的条件下,已知所有学生选课情况,对所有学生的高考课时进行排课并尽可能减少排课失败人数。此时,学校的教学资源约束为:选修课各科目教职工人数,可用于选修课排课的教室总数及每间教室容量。已知条件为学校的年级课表模板(含课时分区方案),高考课和会考课每周的课时数,以及所有学生的6选3情况。
2.1 数学模型
首先定义高考课课表。每位学生都选择了三个科目作为选考科目,因此对于同一个学生而言有三类高考课时,对应三门高考课。定义下面的课程矩阵:

下面介绍如何无冲突地将学生有序放入课程表中。课程表需要满足的硬约束条件如下:
(1)同一时间一个学生不能排两门课程;
(2)同一时间一个教室不能排两门课程;

(4)每一课时任一课程学生数不能超过该教室最大人数r,即:nij≤r(i=1,2,3;j=1,2,…,m)。
其中本文算法满足前两个约束条件。约束(3)为教师约束,它反映了教师资源有限性,为满足此约束应当尽可能使同一时间科目类别多样。约束(4)为教室约束,此约束反应了教室空间的有限性,排课时如不能很好地满足此约束,将增加排课失败学生的人数,对后续排课任务造成障碍。
下面的步骤是向空课表中放置学生。如果无序地放置学生会使算法十分复杂,需要对所有学生进行分类处理,分类的标准是学生选课情况。由于实行走班制的选修课只有六种,因此学生所有的选课情况只有C63=20种。将所有学生先根据选课情况分为20个集合,再根据每种情况的学生人数由大到小对20个集合进行排序。排课时先排人数多的集合再排人数少的集合,这样可以尽可能确保大多数学生成功排课。对于每个学生来说,需要上的高考课只有三种,分别对应高考课的三类课时。因此对同一个学生来说,可以选择的方案只有A33=6种。分别对这六种情况进行分析,分析的方法即为计算每种情况的优先度,最后将采用优先度最高的方案放置学生。放置的方法即为在每个课时查找对应科目的课程,若满足bi j(r-nij) > 0,则向cij的学生列表中添加此学生。如果没有找到,新建一个该科目的课程单元并添加。这样既可以确保同一时间一个学生不排两门课程,满足约束(1),又可以确保同一间教室只上一门课,满足约束(2)。
定义逻辑变量:

其中1表示课时i班级j处的课程科目满足方案,0表示不满足方案。学生插入过程如图1所示。不同颜色代表不同科目,若标1的插入情况表示当前情况,课表每格的数字代表对应课程的逻辑变量l的逻辑值。则可得出当前情况的科目三个课时组合为A、B、C(如右图所示),则在课表中对应可插入的位置坐标是:课时1:(1,1)或(1,6),课时2:(2,3)或(2,7),课时3:(3,3)或(3,7)。遍历所有学生并进行相同操作即可完成课表的生成。
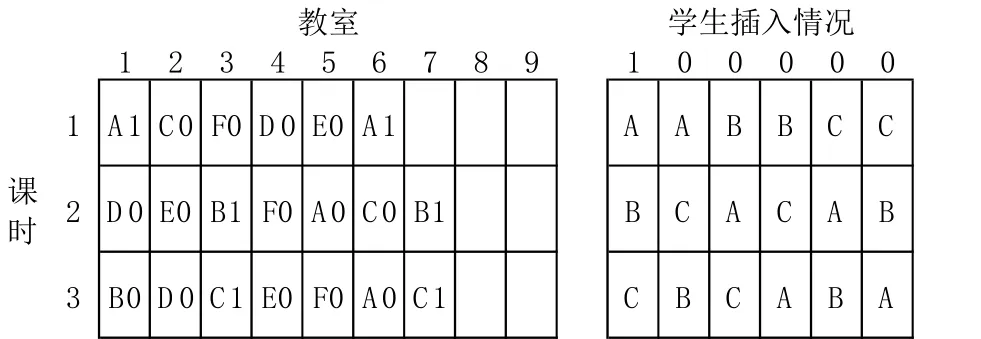
图1 学生插入过程示意图
下面确定优先度的计算方法。优先度是算法的核心,它的定义方法直接决定排课策略的优劣。直观地来看,优先度应当与每个课时教室剩余容量有关。因此定义每种方案的剩余量ζ:

由于要尽可能使科目分布均匀,因此教师修正项为负值。因为一般情况下教师资源相对于教室资源更加充裕,所以教师约束要弱于教室约束,因此设定教师约束项加权k在0到1之间,表示其权重小于教室约束。由上式不难看出,在方案给定的情况下,表达式中参数除k外均为常量。对于不同的初始数据,k的值是不同的。需要在算法中不断改变k的值不断排课,最终取最优解作为最终结果。
2.2 数学模型
算法除去数据输入和输出以外共分两部分,分别是课时生成部分和教师分配部分。课时生成部分算法如图2所示。其中ε为给定的变化单位,为尽可能减少运算次数,实际设定变化量ε=-0.01。生成课表时若返回false,则表明该条件下课表生成失败,立即进入下轮循环。其中,生成课表的算法策略如图3所示。

图2 课时生成算法流图
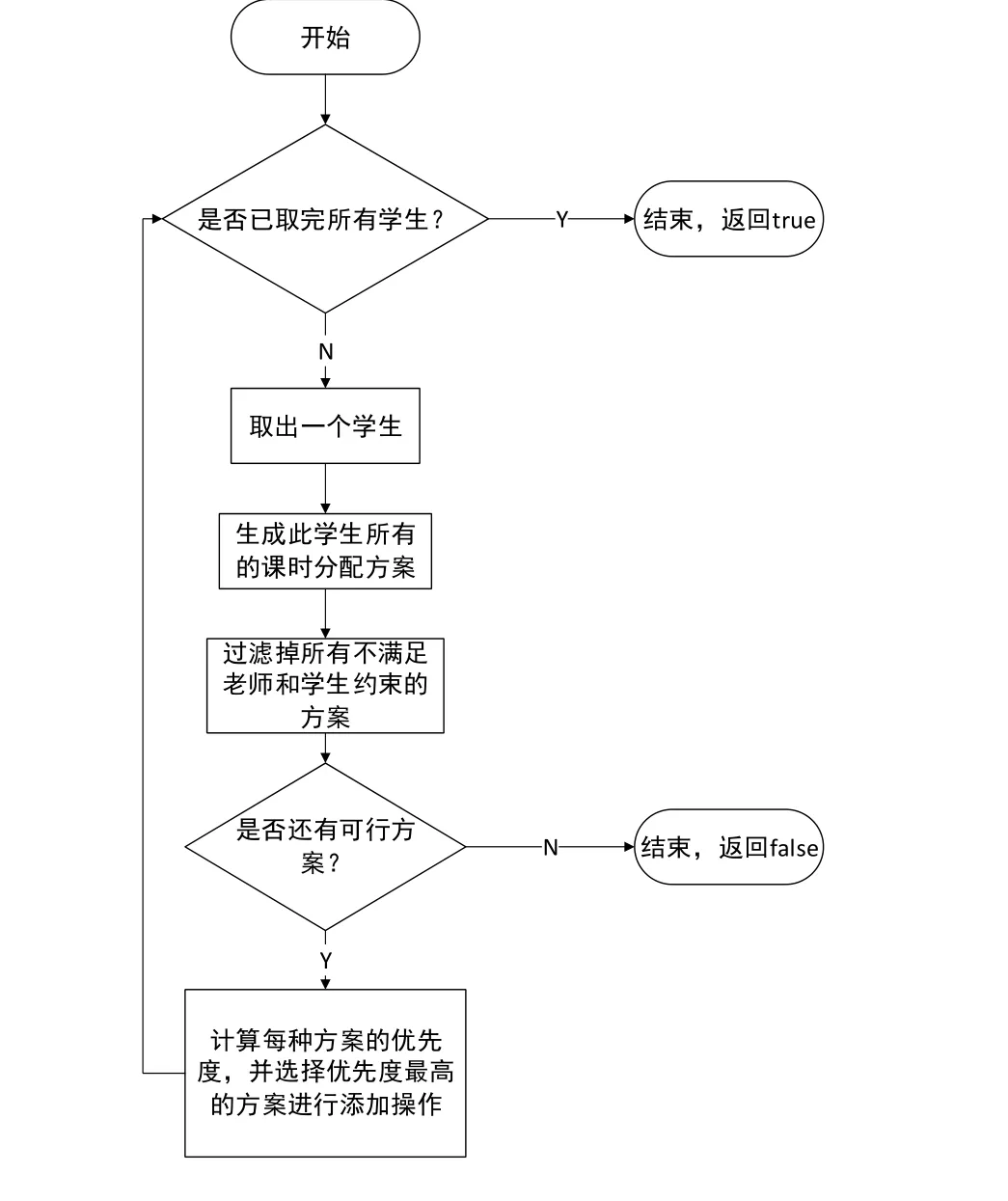
图3 课表生成算法流图
指定的k值下生成课表后,有可能会出现某些教室学生极少的情况,有时一个教室只有不到10人,形成教室和教师资源浪费[11]。此时应当以停开限度作为标准(学生人数小于L的课程应当视为停开),令人数过少的课程停开,然后再尝试将此课程中的学生添加到其他非停开课程中。即需要完成的操作为:
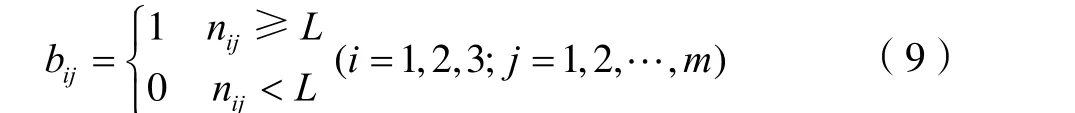
优化过程如图4所示。A格代表停开课程,B格代表因停开而同时改变学生列表的课程,C格代表插入学生的非停开课程。
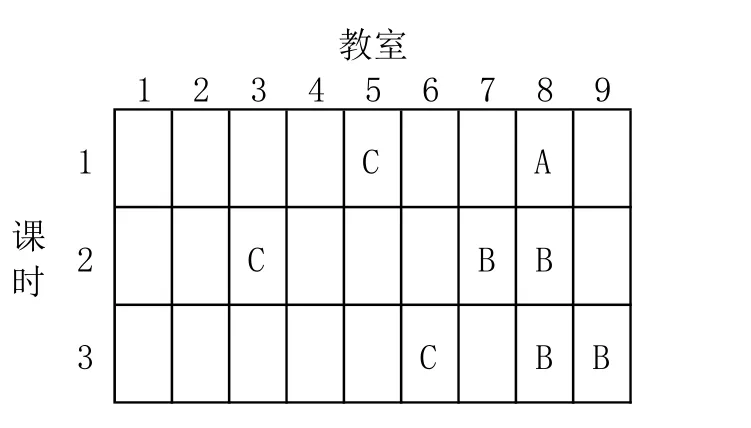
图4 课表优化示意图
优化课表的算法策略如图5所示。
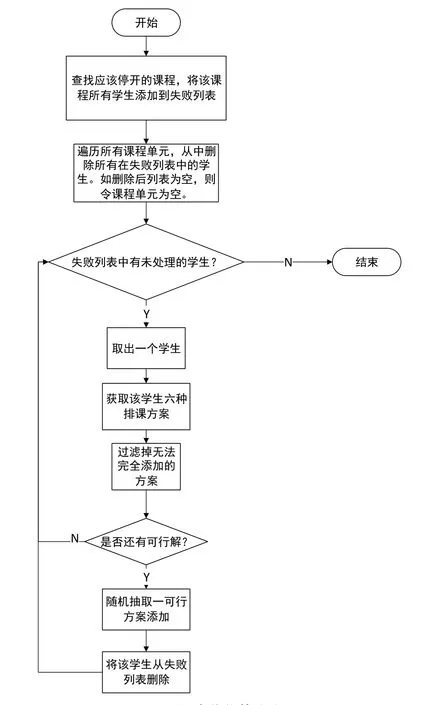
图5 课表优化算法流图
优化后未排入的学生记为排课失败学生。判断课表优劣的指标为排课失败人数,人数越少课表越好。由于课表优化时有可能产生新的停开课程,因此也应将停开课数作为评价标准,停开课数越少的课表越好。评价时首先比较两课表排课失败人数,如排课失败人数相同,比较停开课数。将上述算法策略分别运用于高考和会考情形,就可以分别获得高考和会考课时方案及相应的排课失败学生列表。教师的分配部分如下:首先,由于已满足教师约束,即tj≥si j(i=1,2,3;j=1,2,3,4,5,6),因此一定能成功分配教师。但如果分配时不加策略,将导致教师上课数不均匀,即同一时间只有某几科的教师在上课的情况。为确保教师上课数分配均匀,在随机分配教师后,在每一个选修科目的教师中查找上课数最多和最少的教师,将上课数多的教师的课还给上课数少的教师。重复上述操作,直至最多和最少相差小于等于1。分别在高考和会考的情况下完成上述操作,即可得到一个教师分配均匀的方案。
3 数值仿真
3.1 算例设置
本次实验的目的有两个:
(1)检验算法可行性,依据实例数据给出排课方案。
(2)找到合适的停开限度设置策略并改进算法,并得到较优解。
本次实验采用某校某年级真实选课数据,包括1451名学生,选修教师43人,32间教室,每间教室容量55人。其中学生选课结果统计和每科教师人数如表1所示,此处只列出选择指定高考课的学生人数。
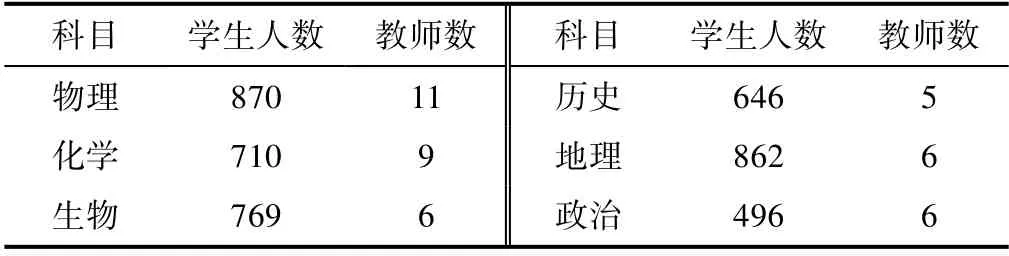
表1 实例1原始数据表
为证明本系统能够在学生人数较少时获得可行解。本实验对真实数据进行精简获得另一份测试数据。测试数据包括248名学生,选修教师18人,9间教室,每间教室容量45人。其中学生选课结果统计和每科教师人数如表2所示。
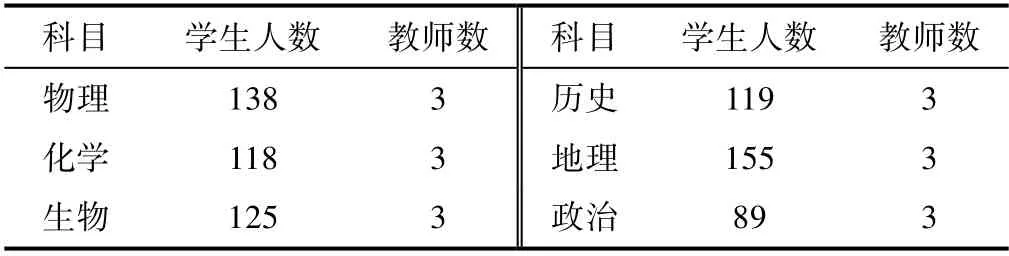
表2 实例2原始数据表
3.2 数学模型
首先,实例1在min≤ 19、实例2在min≤ 25时会考、高考均无排课失败学生,且满足所有约束。其次,在没有排课失败学生的前提下,评判最终课表优劣的标准为教室资源利用率。为方便绘图,以冗余率作为标准。教室资源冗余率η定义如下:

本次仿真设定的优化次数为1次,改变停开课程限度直至高考或会考课表出现排课失败学生。以冗余率为因变量,得到散点图。用最小二乘法拟合曲线如图6、图7所示。
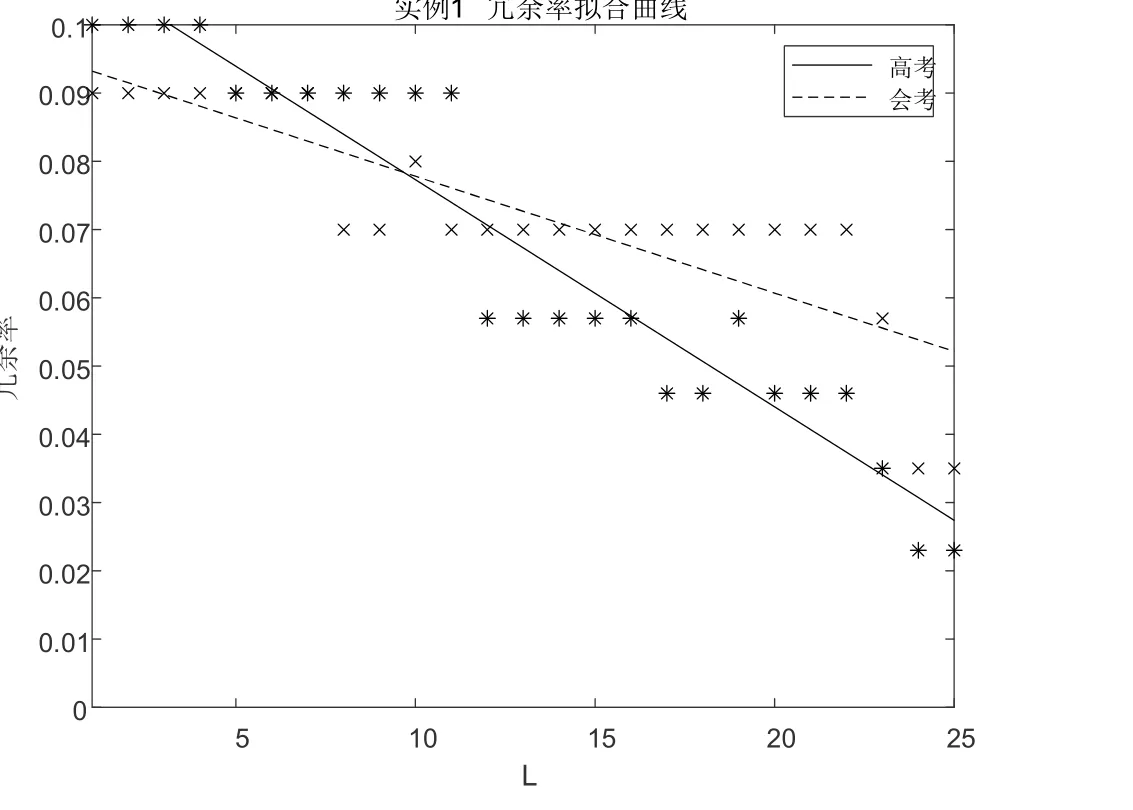
图6 实例1冗余率拟合曲线
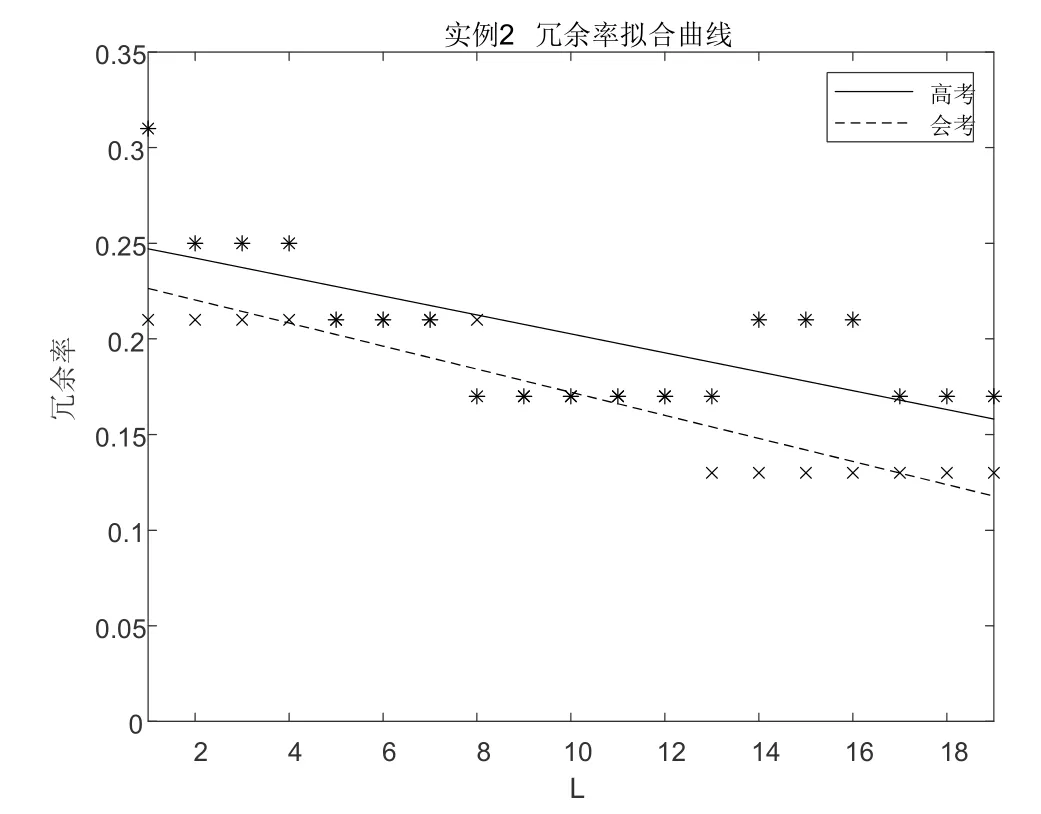
图7 实例2冗余率拟合曲线
分析实例1或实例2的冗余率拟合曲线可知,在不出现排课失败学生的前提下,停开限度越高冗余率越低,排课效果越好,这与直观判断相符。为获得本算法下的较优解,改进图1所示算法如图8所示。改进的部分是在不出现排课失败的前提下不断提高停开限度,取停开限度最高的方案作为最终解。
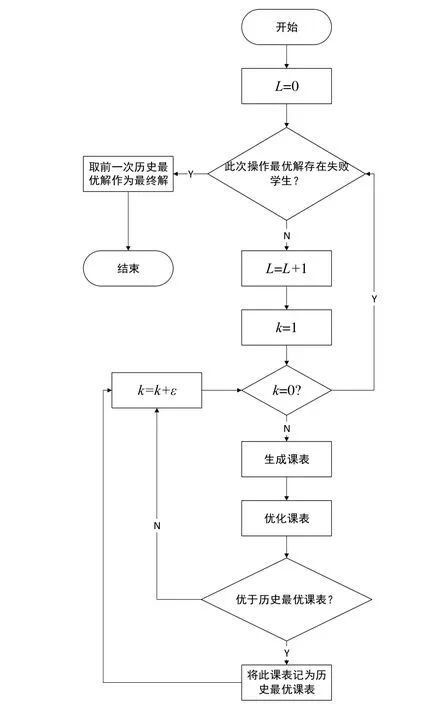
图8 课时生成改进算法流图
依照上图方法可以无须设置停开课程限度,直接获得该算法策略下的较优解。运行程序得到的部分结果如表3、表4所示。
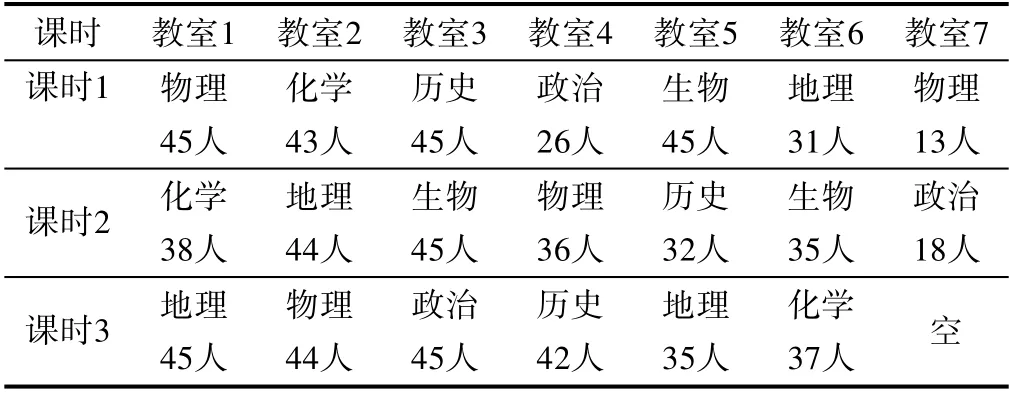
表3 实例2课时方案
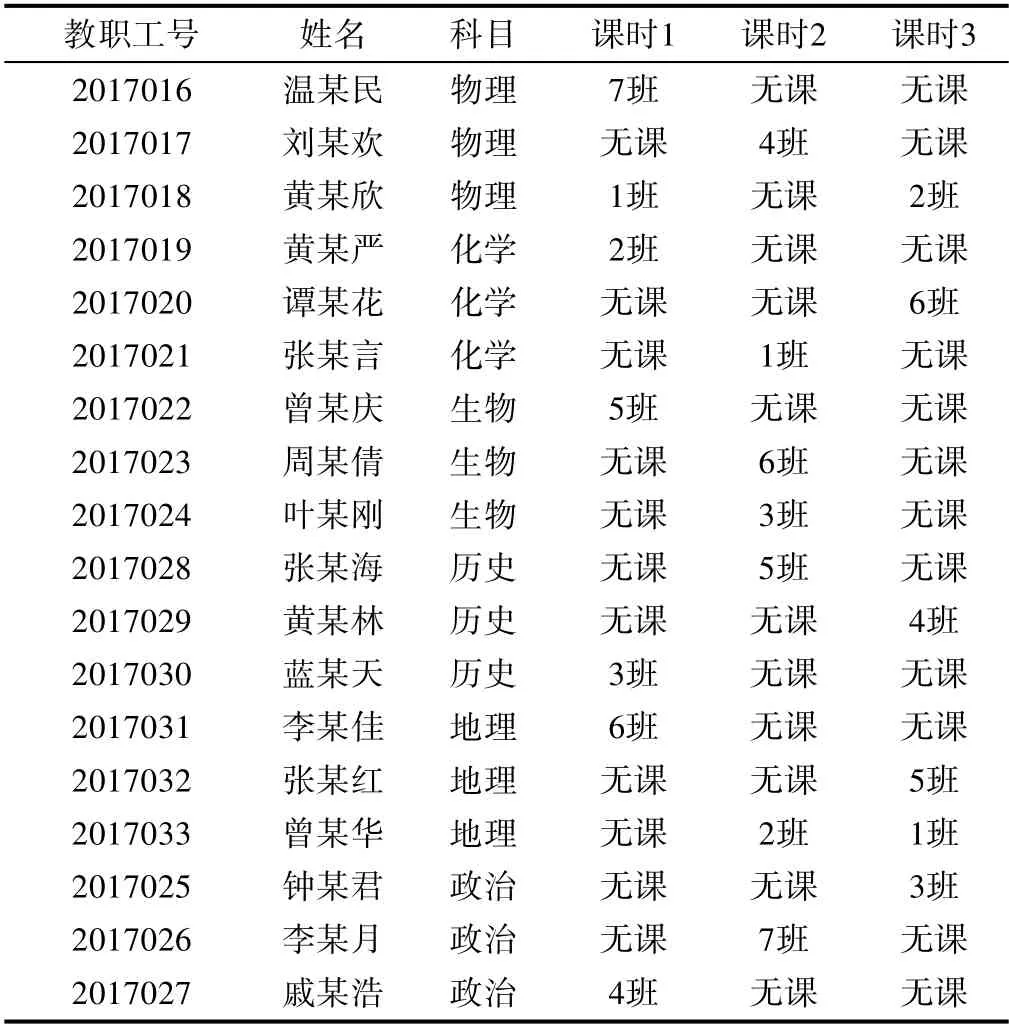
表4 实例2教师分配方案
3.3 仿真讨论
算法策略能够成功完成两组实例下的高考和会考排课任务,验证了算法的有效性;并且分析得到停开课限度与教室资源利用率之间的关系,从而改进算法以获得较优解。
在获得高考和会考的三类课时并分配教师完毕后,在高考和会考课时区中分别依照时间顺序周期地填充课时,填充的轮数为一个高考或会考科目一周内的总课时数。这样处理的好处是无论课时区在时间顺序上的罗列情况如何,都能够保证同一个教师不会在上完一个班的课后再给此班级上课,实现了教案对齐的实际需求,并尽可能保证了每个科目课时均匀。选修课时区的规划可以依照学校的具体需求设计,但应保证不在相应教师的非排课时间之内。此部分内容与本文算法无关,不再赘述。
4 结论
本文给出了一种走班制下选修课排课的优化度排课算法,并通过数值算理验证了该算法的有效性。为直接得到算法策略下的较优解,算例还验证了停开限度对教室资源利用率的影响,实现更加智能的排课过程。本文算法的优点在于1、满足学生的选课需求,完成走班制下的排课任务。2、算法运行时间短,实现简单。但此算法也存在缺点1、固定班教学与走班教学分立,不能做到同一时间既有走班也有固定班。2、教室空间资源存在冗余。此外,本文没有讨论分层教学(不同水平的学生在不同的班)、合班课程(两个班级在一个教室同时上课)、教师水平区分(不同教学水平的教师分派不同的教学任务)等更深层次的排课需求,后续还应解决诸如此类学校排课的个性化问题。

