不同波幅条件下内孤立波对柱体作用机制研究

王 寅，沈火林，王玲玲，计 勇，席芝橙，张雯雯

(1.南昌工程学院 水利与生态工程学院，江西 南昌 330099；2.河海大学 水利水电学院，江苏 南京 210098)

在稳定分层的流体系统中，外界微小的扰动可在密度分界面(密度跃层)上引起携巨大能量的内波现象[1]。内孤立波系波幅大、周期短、所携能量大的一类非线性内波[2]。该类波在传播时所产生的作用力可对近岸及河口复杂水动力环境下水下支撑结构物的安全稳定性造成严重的威胁[3]。

相关学者就柱体在内孤立波环境下的受力问题开展了系列理论研究。蔡树群等人运用Morison公式估算了内孤立波对柱体的作用力，基于该半经验半理论公式求解出小尺度圆柱受力的垂向分布[4-5]。但在采用Morison公式时，形状阻力系数CD和惯性力系数CM虽可通过相关的试验结果进行选取，但此类试验都在非内孤立波环境下进行。内孤立波所诱发的分层流环境下的流场与密度均一流环境差别较大[6]，两个受力系数是否适用于内孤立波对柱体的作用问题尚无定论；同样采用Morsion公式计算内孤立波对柱体的作用力，Du[7]得到内孤立波作用效果大约与波长为300 m，波高为18 m的表面波所致荷载相等，而Song[8]发现内孤立波作用效果远弱于表面波，约为9%。可见，即使计算结果可定性计算出柱体所有内孤立波的作用力，但在定量上还不够准确。采用更精细的计算方法获取内孤立波对柱体的作用机制势在必行。

本研究在构建三维数值内波水槽的基础上，采用大涡模拟(large-eddy simulation，LES)技术，模拟内孤立波的产生和传播，研究不同内孤立波波幅(ηo)对柱体水动力荷载的影响。对比分析各工况下柱周水动力特性，提取相关水动力参数云图及矢量图，深入剖析柱体在内孤立波环境下的受力规律。

1 数值方法

1.1 Navier-Stokes方程(N-S方程)

基于连续性假设，在三维瞬态流动时，用于描述不可压缩粘性水体的Navier-Stokes(N-S方程)可表达为

(1)

(2)

式中ρ为密度项；t为时间；xi，xj为笛卡尔坐标系的3个坐标方向；ui，uj为笛卡尔坐标系中的3个流速分量；p为压力项；μ为动力粘性系数；fi为i方向的单位体积力。

1.2 标量输运方程

由于标量(温度或浓度)而导致的流体分层现象，以密度跃层为界线，上、下层流体之间会进行质量交换和对流—扩散，而标量输运方程则和它们紧密相连，即：

(3)

ρ=C+ρ0，

(4)

式中C为盐度，kg/m3；k为分子扩散系数；S为源项；ρ为水体密度，kg/m3；ρo为清水密度，kg/m3。

1.3 大涡模拟(LES)控制方程

大涡模拟技术是对湍流脉动的一种空间平均，经滤波函数将大尺度涡和小尺度涡分离开来[9]。过滤后的动量和质量方程可表示为

(5)

(6)

(7)

2 数学模型

2.1 三维模型的建立、造波方法及工况设置

本研究所建立的三维数值波浪水槽长(X)、宽(Z)、高(Y)为：12 m×0.6 m×0.8 m，见图1。所研究的柱体位于槽宽(Z)中心，其底部的中心点坐标为：(x，y，z)=(6，0，0.3)，坐标原点为图1中的左里下角。柱体直径D=10 cm。

图1 三维数值波浪水槽示意图

定义该柱体在内孤立波环境下所受到的无量纲水平合力CFn的计算公式为

(8)

式中Fn为数值模型计算所得的柱体水平合力(N)；g为重力加速度(cm/s2)；A为柱体的迎风面积(cm2)；H为水槽总水深(cm)。

本研究所制造出的内孤立波波形为下凹型，数值模型中分层水体基本参数设定为：水槽总水深H=80 cm，其中上层水体密度ρ1=0.998(g·cm-3)，水层厚度h1=20 cm；下层水体密度ρ2=1.017(g·cm-3)，水层厚度h2=60 cm，数模整体布局如图2所示。采用重力塌陷法制造内孤立波[10]。为制造出下凹型内孤立波，需把水槽在纵向分为造波区和传播计算区两部分，并使造波区密度跃层位置低于传播计算区密度跃层位置，如图3所示。定义造波区与传播计算区密度跃层高度差ho称为阶跃高度，造波区长度Lo为阶跃长度。具体计算参数及工况设置见表1，其中ηo为内孤立波波幅，ηo/H为相对波幅。

图2 数值模型布局

图3 重力塌陷法制造下凹型内孤立波示意图

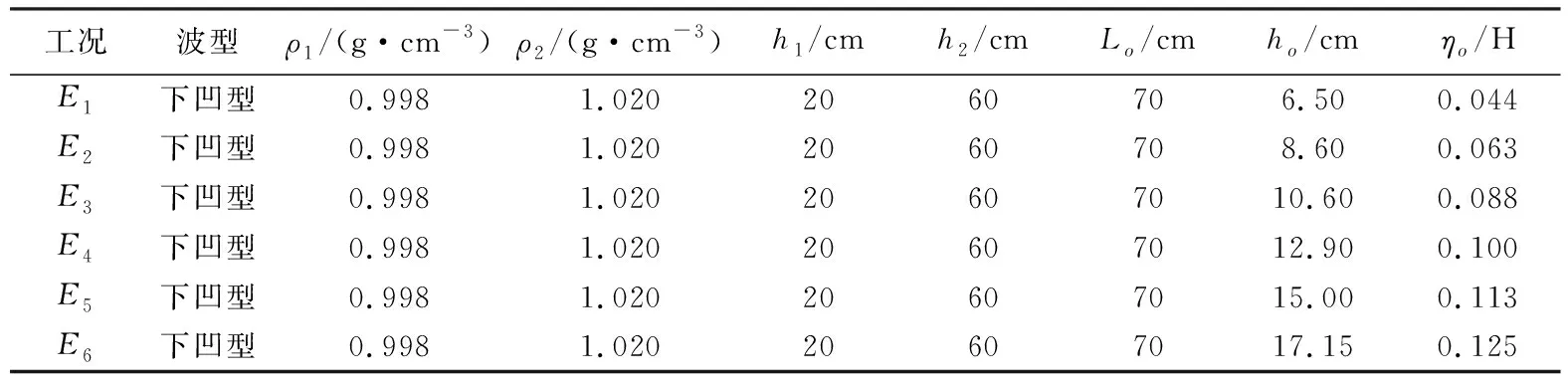
表1 数值模拟工况及相关参数

2.2 数值方法和边界条件

采用大涡模拟(LES)技术实现三维数值波浪水槽中下凹型内孤立波的形成和传播；为保证数值计算域的质量守恒，研究采用SIMPLE算法耦合N-S方程中的流速—压力项，以此得到压力场；利用二阶中心差分格式对空间进行离散，时间的离散采用隐式格式。造波区左边壁、槽底、柱体表面采用无滑移固壁边界，水槽侧壁采用滑移固壁边界。水槽右边壁采用Sommerfeld辐射型边界[11]，以此可防止内孤立波再反射，保证数值计算的精度；由于本研究中表面波波幅很小，影响甚微，水面采用“刚盖”假定忽略表面波的作用[12]。

2.3 模型验证

网格无关性分析及物理模型试验对数模的验证参照笔者之前发表的文章[13-14]，本文所采用的模型设计参数与两篇文献[13-14]一致。

3 数值结果及分析

3.1 各工况下CFn历时曲线对比图分析

图4给出了不同波幅ηo/H工况下，柱体所受内孤立波无量纲水平合力CFn随时间的变化曲线。当内孤立波传经柱体时，柱体所受的阻力与波幅成正比，均经历了先减后增、再减再增、最后趋于0的过程。由此判断，内孤立波会对柱体产生剪切及振荡作用。此外，各工况下柱体的受力趋势相似，且ηo/H越大，柱体达到其受力峰值时间越早。说明波幅越大，波的传播速度越快，柱体所受阻力曲线的峰值越大，其衰减也越快。另外，随着内孤立波的传播，其波动程度逐渐减小。这是由于以密度跃层为界的两类不同密度水体的相互作用效果远强于气水交界面处气体与水体的相互作用，更强的粘性耗散导致内孤立波波幅更快的衰减。

柱体所受水平力变化可分解为3个过程：(1)内孤立波抵达柱前：随着内孤立波逐渐接近柱体，柱体所受水平力逐渐增大。当内孤立波与柱体接触时，水平力达到其第一个峰值，即图中的CFn-max；(2)在孤立波穿越柱体时：上、下两层流体流速反向，柱体随之承受一个方向为右的反作用力，逐渐抵消柱体左向水平力。随后水平力变为0，继而达到水平力谷值。(3)内孤立波穿越柱体后：左向作用力持续增大，逐渐抵消右向作用力。水平力逐渐变大，在内孤立波离开柱体时水平力达到其第2个峰值。最后由于尾波的存在，引发水平力的震荡作用。不同波幅工况下，水平力均出现峰值及谷值。

3.2 各工况下压强云图对比分析

图5给出了槽宽中心(Z=30 cm)截面的压强云图。各工况下(E1～E6)压强分布图均相同。数值水槽水深为80 cm，水面相对压强为0 Pa，槽底相对压强为7 840 Pa，符合实际情况。

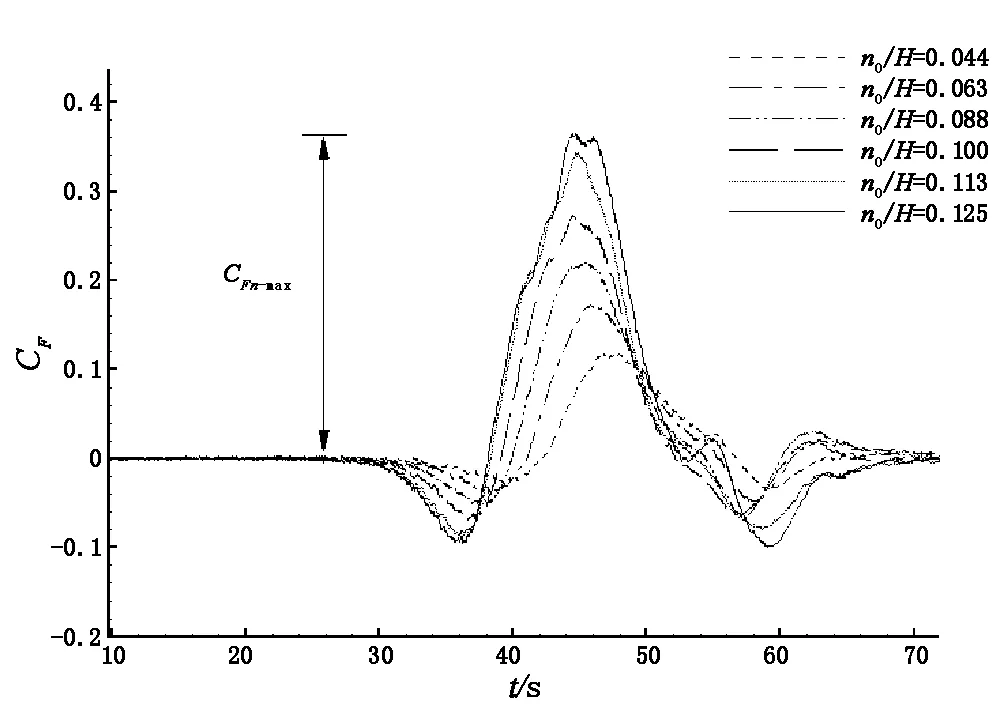
图4 各工况下CFn历时曲线对比图

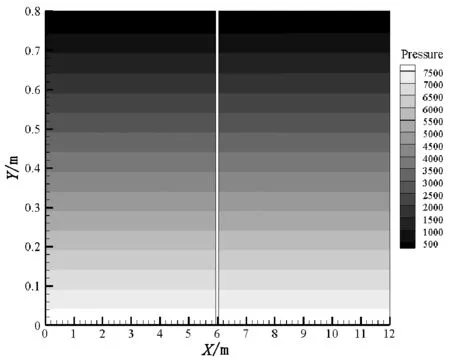
图5 横向(Z=30 cm)截面压强云图

3.3 各工况下密度云图对比分析

图4中CFn-max表示内孤立波无量纲水平合力峰值，本文数模数据提取及云图绘制的特征时刻皆为柱体受力达到其峰值CFn-max所对应的最不利时刻，即CFn=CFn-max时刻。表3给出了各工况之间跃阶高度ho之比hoi/hoi+1与波幅ηo之比ηoi/ηoi+1的对应关系。图6(a)～(f)给出了不同波幅工况下柱体CFn=CFn-max时刻槽宽中心(Z=30 cm)截面的密度云图。由图6可知，随着跃阶高度ho的增大，波幅ηo不断增加。

表3 ho之比与ηo之比对应关系

由此可知hoi/hoi+1越大，ηoi/ηoi+1越大。越大的跃阶高度ho可激发更大波幅的内孤立波，且波幅增幅随跃阶高度的增大呈抛物线分布。

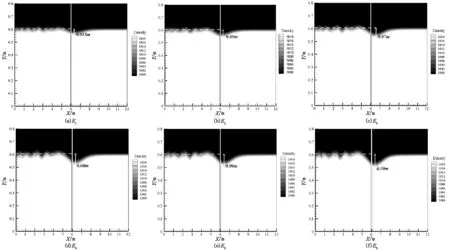
图6 不同波幅工况下横向(Z=30cm)截面密度云图(CFn=CFn-max时刻)

3.4 各工况下速度云图对比分析

图7给出了不同波幅工况下柱体CFn=CFn-max时刻Z=30 cm截面的速度云图。如图7所示，以密度跃层为界，上下水层流速反向。上层速度为正，下层速度为负，上层水体的流向与内孤立波的波向一致，且上层水体速度绝对值要大于下层。此外，对比图7(a)～(f)可以看出，随ho不断增大，上下水层流体质点速度不断增大，其中当ho=6.5 cm(工况E1)时，上层最大流体质点速度为0.024 9 m/s，下层最小流体质点速度为-0.011 85 m/s；ho=17.15 cm(工况E6)时，上层最大流体质点速度为0.058 6 m/s，下层最小流体质点速度为-0.037 6 m/s。表4给出了各工况波幅之比ηoi/ηoi+1与上、下水层质点最小流速Vmin之比、最大流速Vmax之比的对应关系。

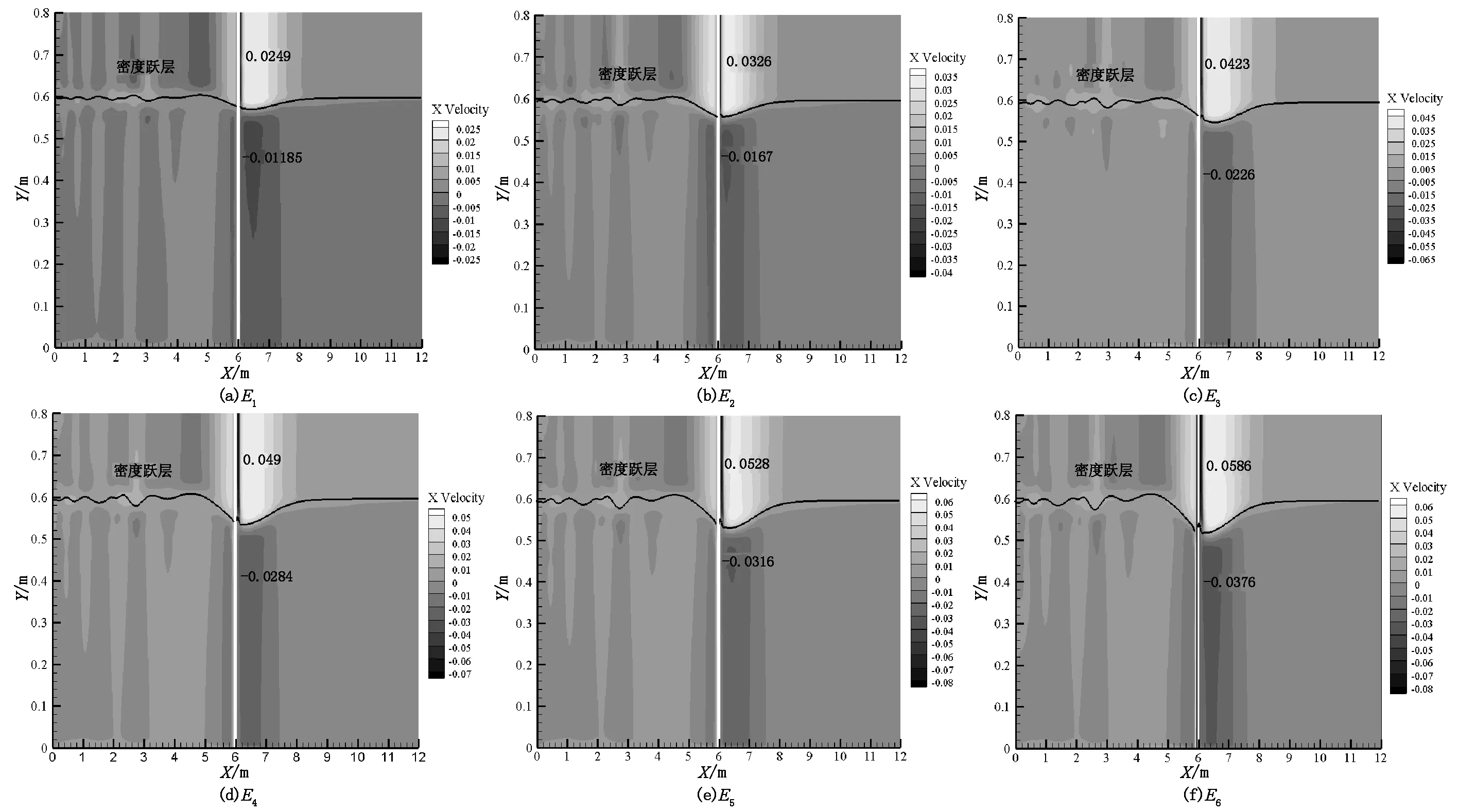
图7 不同波幅工况下横向(Z=0.3 m)截面速度云图(CFn=CFn-max时刻)

表4 ηo之比与V对应关系

由此可知，流体速度与波幅成正比；hoi/hoi+1越大，流体Vmin和Vmax越大，且两幅值的增幅也逐渐变大。说明波幅越大的内孤立波能激发出更剧烈的流场。

3.5 各工况下流线图及速度矢量图对比分析

图8(a)～(f)及图9(a)～(f)分别给出了不同波幅工况下柱体CFn=CFn-max时刻Z=30cm截面的流线图及速度矢量图对比。如图8所示，密度跃层上、下层水体流动反向，流动转向发生在跃层附近；而在绕流作用下，无论是上层水体或下层水体，柱前、柱后均会产生漩涡，从而导致柱前、柱后流向一致；截面速度矢量总体上呈现出一个顺时针方向的旋涡，旋涡的存在加剧水体紊乱，产生能量损失。柱前下层流体质点速度较小，柱后层流体质点速度较大。此外，随着波幅η的不断增大，流体各部分质点速度矢量均不断增大。

同时，距离密度跃层越近，内孤立波波动影响越大。在流场中的流体质点的运动速度越小，即在垂向位置上，随着与密度分层面距离的增大，水平速度值不断减小。综合图8～9的流线图及速度矢量图可知，密度跃层的上、下水层流速反向，这也是在内孤立波环境中可诱导出强烈剪切流的根本原因所在，剪切作用致使水下结构物剪切疲劳甚至发生破坏。

图8 不同波幅工况下横向(Z=0.3 m)截面流线图(CFn=CFn-max时刻)

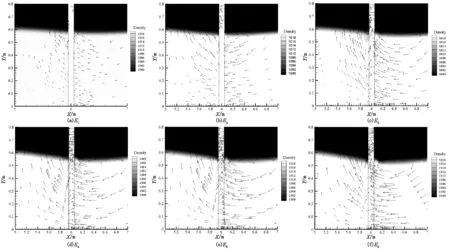
图9 不同波幅工况下横向(Z=0.3 m)截面速度矢量图(CFn=CFn-max时刻)

4 结束语

借助三维数值波浪水槽，通过绘制密度云图、速度云图、流线图及速度矢量图深入研究了不同内孤立波波幅(ηo)对圆柱作用力的影响。相比过往研究，本文给出了一定的量化结果，细致对比了不同波幅工况下的流场特性，得到如下结论：

(1)两工况跃阶高度ho之比hoi/hoi+1越大，波幅ηo之比ηoi/ηoi+1越大。说明跃阶高度是波幅大小的主要控因；

(2)对比不同波幅下柱体的受力历时曲线，ho越大，ηo越大，波的传播速度越快，柱体所受阻力的峰值也越大，表明波幅与柱体所受水平作用力成正比。同时大波幅工况下，柱体受力的衰减幅度也越大。

(3)从提取的流线图及速度矢量图可知，以密度跃层为界，上层水体质点速度为正，下层水体质点速度为负，导致内孤立波具有巨大的剪切力，易对水下结构物造成破坏。随着波幅ηo的不断增大，流动区域的水动力越剧烈，上、下水层流体质点速度不断增大。