颗粒粒径对深海采矿矿浆泵性能的影响①

吉成才， 关英杰， 郑 皓， 张 明

(长沙矿冶研究院有限责任公司 深海矿产资源开发利用国家重点实验室,湖南长沙410012)

随着陆地矿产资源的衰竭,深海矿产资源开发技术越来越被世界各国所重视［1］,目前最有商业前景的开采方案是管道提升法［2-3］。 矿浆泵作为采矿输送系统中最核心的动力装备,其水力结构复杂,颗粒极易堵塞泵管流道。 国内开发的矿浆泵过流和回流能力往往不足,导致流道堵塞［4-5］。 流道堵塞与颗粒及颗粒群的流态、颗粒流的时空分布和动态迁移直接关联,要解决上述工程问题,必须从泵内颗粒两相流的深层规律和堵塞机理上深入研究。

目前对于深海矿浆泵的研究,主要是基于传统的固液两相流模型［6-10］。 深海采矿矿浆泵带有空间导叶,与普通的蜗壳式离心泵结构有较大差别,输送工况也具有大颗粒低浓度的特点,目前将离散元和流体动力学耦合方法应用到矿浆泵流场数值计算中的研究还不多。 本文采用CFD-DEM 耦合算法对矿浆泵内颗粒运动特性进行数值模拟,分析颗粒粒径对矿浆泵内流动特性的影响,并分析流道堵塞的机理,旨在为未来的深海采矿工程泵开发提供理论依据。

1 理论与模型

1.1 计算模型

CFD-DEM 耦合算法的求解策略由CFD 求解器求解连续相、由DEM 求解器求解离散相,所以CFD-DEM求解分为3 个部分:连续相求解、离散相求解和两相间的耦合。

流体连续相求解主要应用连续性方程和动量方程(Navier-Stokes 方程)。

连续性方程又称为质量守恒方程,其表述为:

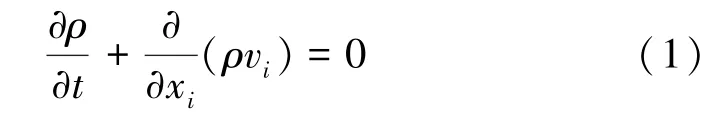
式中ρ 为流体密度；t 为时间；vi为速度矢量在笛卡尔直角坐标系i 方向的分量。

动量守恒方程也称作Navier-Stokes 方程,x、y、z 3 个方向的动量守恒方程为:

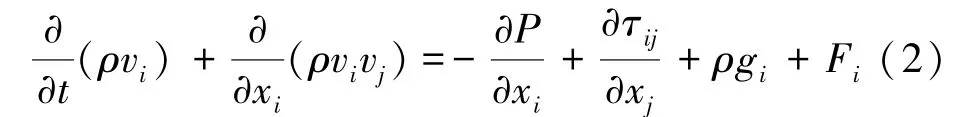
式中P 为静压；ρgi和Fi分别为i 方向上的重力体积力和外部体积力；τij为由流体运动引起的黏性应力张量。

离散相的求解主要是通过接触模型求解颗粒碰撞过程的受力,并运用牛顿第二定律计算出颗粒的加速度,然后更新颗粒的速度和位移。 对粒子的受力进行分析,其对应的动量守恒和角动量守恒方程为:

式中mi、vi分别为颗粒的质量和速度；Fn,ji为颗粒间的法向接触力；Fτ,ji为切向接触力； Ii为颗粒的转动惯量； ωi为颗粒的角速度； ri为颗粒半径,Ffp,i为来自液相对颗粒的作用力；Mi为滚动摩擦力矩。

CFD-DEM 的计算核心在于两个物理场的数据交换,在每个时间步长中,首先CFD 求解器计算连续相流场,仿真迭代至收敛,然后将网格单元的流体条件传递给DEM 求解器,从而计算出作用在颗粒上的阻力,并将此力代入颗粒运动方程,求解离散相的位置、速度等信息。 DEM 迭代计算结束后,估计出计算单元内的孔隙率并连同相间作用力传递回CFD 求解器。 CFD求解器利用这些数据求解连续相流场,更新流动区域,以此循环进入下一个时间步长。

1.2 模型与网格划分

深海采矿矿浆泵的结构如图1 所示。

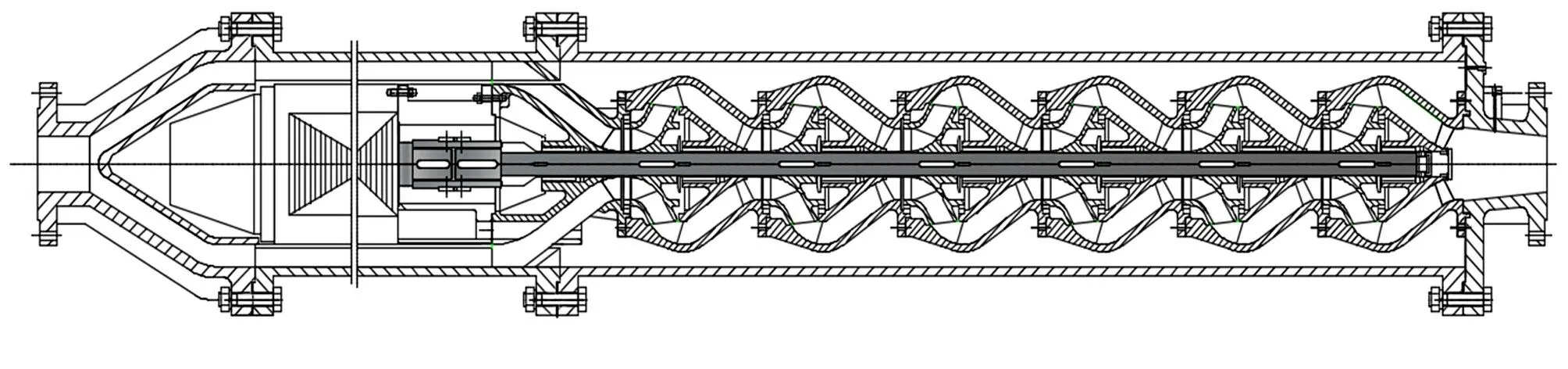
图1 深海采矿矿浆泵结构示意

依据我国“十三五”深海采矿重点研发计划中扬矿泵的工况参数,按照相似原理,限定二者比转速相同,设计模型泵进行计算和试验研究。 模型基本参数为:流量Q＝120 m3/h,扬程H ＝20 m,转速n ＝1 450 r/min,输送浓度5%～15%,输送颗粒粒径小于20 mm。 模型水力部件的主要几何参数如表1 所示。

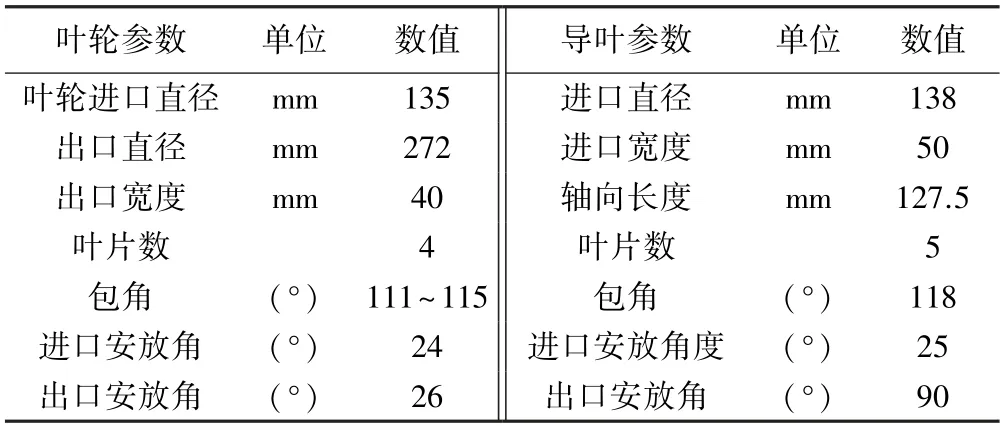
表1 矿浆模型泵主要几何参数

流场计算域由进口延长段、叶轮、空间导叶、出口延长段组成,整泵竖直放置,进口端处于最下方,浆料垂直提升。 将构造的流体计算域三维模型导入ICEM软件中进行计算网格划分,得到如图2 所示的网格单元。 DEM 是一种无网格方法,需要消耗大量的计算资源,在CFD-DEM 耦合计算中70%左右的时间耗费在DEM 求解中。 网格数过多,每个时间步长内CFD-DEM之间都需要进行大量的数据交换(如计算连续相各网格内的空隙率和固相平均速度等),耦合模拟非常缓慢；网格单元过小,颗粒将占据网格单元大部分体积,此时较高的空隙度将导致DEM 求解不稳定,所以网格选择应在CFD 应用基础上寻求较粗糙网格为宜。 本文计算模型网格经历了无关性分析,最终网格单元总数为54 163。

图2 流动域三维造型

1.3 计算参数设置

选取常温清水作为连续相,泵入口固相体积浓度为5%。 设定颗粒为球形,选用5 mm、10 mm、15 mm 3 种粒径颗粒,颗粒与颗粒、颗粒与泵体间的碰撞采用Hertz-Mindlin 无滑动接触模型。 泵体材料、颗粒物料的有关参数见表2,颗粒与颗粒、颗粒与泵体间的相互影响系数见表3。

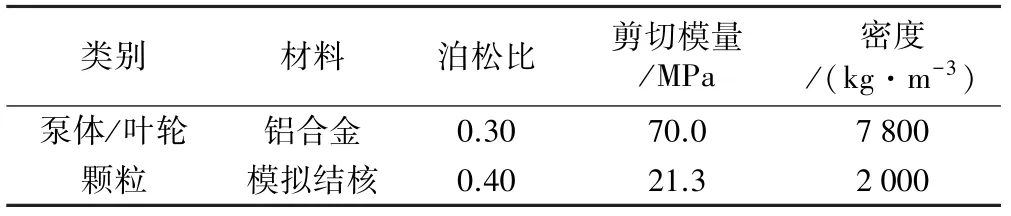
表2 物性参数

本文运用Fluent 和EDEM 耦合计算对模型泵进行非定常计算,总体时间5 s(约120Tn,Tn 为叶轮旋转一周的时间),流体计算时间步长设置为0.000 1 s,约为叶轮旋转1°的时间步长。 EDEM-Fluent 耦合计算中颗粒计算时间步长要求不能大于流体计算时间步长,参考瑞利时间步长大小,5 mm 粒径工况时间步长设为0.000 05 s,10 mm 和15 mm 粒径工况时间步长设为0.000 1 s,颗粒计算时间步长控制在瑞利时间步长的60%以内。 湍流模型采用RNG κ-ε 模型。 叶轮设置于旋转坐标系中,导叶处于静止坐标系中。 重力加速度为9.81 m/s2,重力方向与泵进口方向相反。 进口边界采用速度入口,假定进口处的流动是轴对称和无预旋的,出口边界采用自由出流边界。 壁面处默认为无滑移边界条件,近壁处采用标准壁面函数处理。

2 CFD-DEM 的泵内流场计算

颗粒在泵内的空间分布、运动特征对于整机的性能,包括正向流动的通畅性和过流壁面的磨损等特性影响很大。 对于给定的流道,相同浓度下,颗粒粒径越大则颗粒数越少,反之则越多；颗粒越大,流体拖曳其迁移所需要的动能也将越大；局部浓度偏大将容易导致流道堵塞。

2.1 不同颗粒粒径的空间分布

对3 种粒径下矿浆泵内的颗粒情况进行分析,泵内的颗粒体积浓度随运行时间变化情况如图3 所示。矿浆泵初始工作的一段时间内,泵内颗粒相体积浓度逐渐升高,在运行一段时间后,浓度不再继续增加,结合数值计算的残差收敛特征,当数学收敛和物理收敛均达到要求时,认为计算稳定。 由图3 可知,不同粒径下的颗粒体积浓度数值呈现一定的波动,且波动幅度随颗粒粒径增大而增大。

对3 种工况在颗粒体积浓度相对稳定的时间段内(1～5 s)进行分析,得到不同工况下的平均浓度如表4所示。 随着颗粒粒径增加,颗粒体积浓度也逐渐升高,但均高于入口处的体积浓度(5%),说明泵内颗粒有局部聚集的情况,且随粒径增加,聚集更加明显,但各部分浓度保持基本恒定,说明流道并未发生堵塞。 图4 为泵流道内各部分的颗粒相对体积浓度,可见相对体积浓度从大到小排序为:进口＞叶轮＞导叶＞出口。

泵内各部分的颗粒空间分布如图5 所示,在进口、导叶及出口段,颗粒体积浓度均随着颗粒粒径增大而增高。 在进口延长段,颗粒与清水以相同速度射入,由于重力的作用,颗粒会发生“沉降”,颗粒越大,沉降速度越大。 颗粒由进口延长段入口到叶轮入口,颗粒相速度下降,且颗粒越大,下降幅度越大。 经统计,5 mm,10 mm 和15 mm 粒径颗粒在该区域的垂直方向平均速度分别为2.07 m/s,1.97 m/s 和1.89 m/s,均低于该区域清水流速(2.33 m/s)。 因此,该区域的颗粒相体积浓度大于入射状态的5%,且粒径越大,浓度越大。

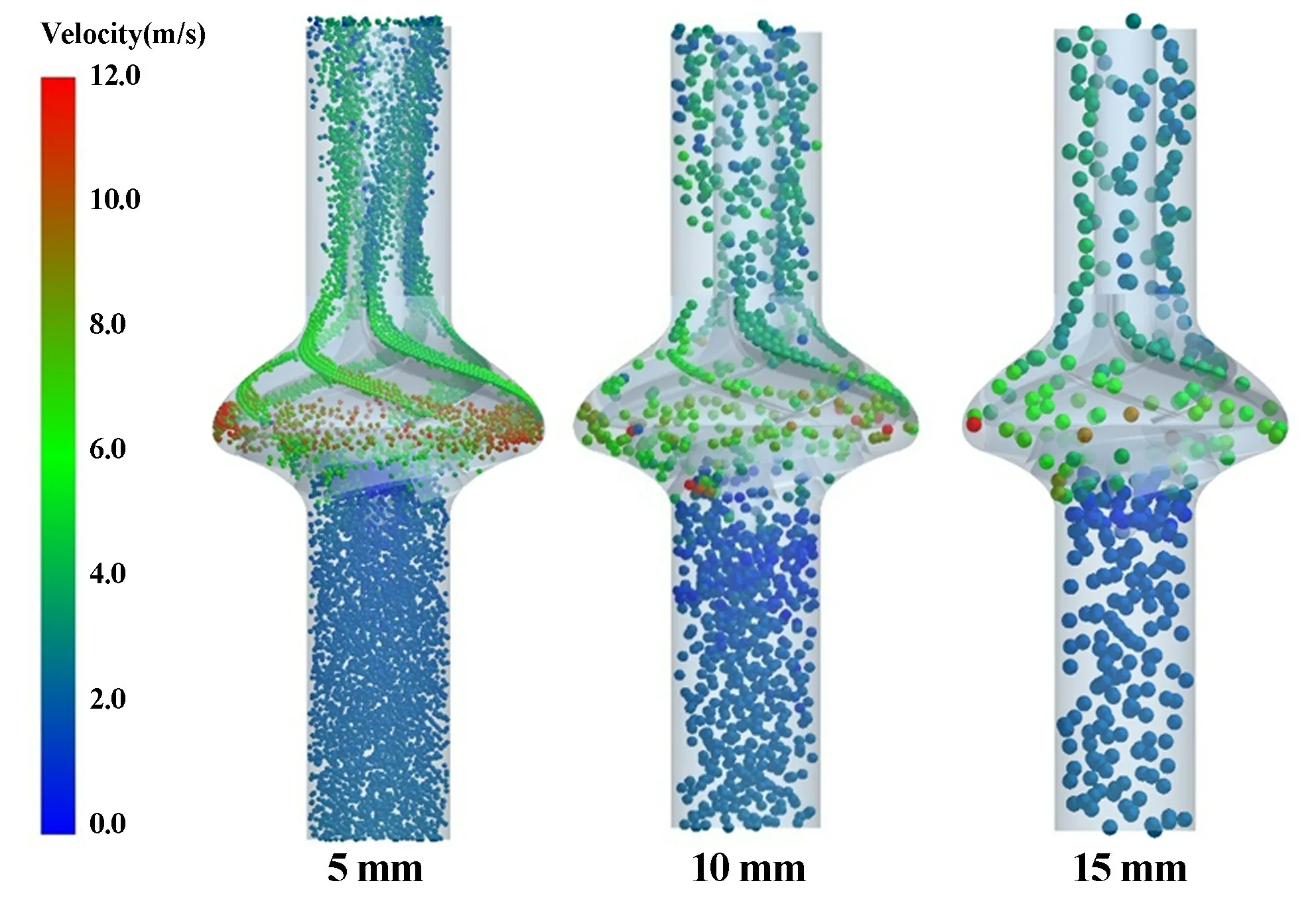
图5 不同粒径颗粒工况矿浆泵内颗粒分布

2.2 不同颗粒粒径下运动特征

在总体体积浓度相同的条件下,小颗粒数量更多,大颗粒数量较少(单个颗粒的体积比值为1 ∶8 ∶27),图6 为叶轮内的颗粒分布,它展现出两个显著特征:一是叶片进口位置低速颗粒聚集,二是流道中部小颗粒贴近工作面移动,而大颗粒则相对均匀分布。 关于叶片头部颗粒聚集效应,可认为颗粒低速进入流道时,先进入的颗粒与叶轮头部和盖板发生碰撞,反弹后会与后进入的颗粒再度碰撞,碰撞次数随着颗粒数增加而增加,这种聚集和堵塞反过来又对流体起到了加速的作用。 关于流道中部颗粒的运动和分布,大颗粒在流道中的速度显著低于小颗粒,表明其获得的能量也更少,但是其空间分布相对于前者更加均衡。

图6 叶轮内颗粒的空间分布

图7为导叶流道内的颗粒空间分布。 大颗粒工况颗粒体积浓度大于小颗粒体积浓度。 经统计,5 mm,10 mm 和15 mm 粒径颗粒在导叶流道内的平均速度分别为9.20 m/s,8.83 m/s 和7.12 m/s。 颗粒在导叶流道内沿着导叶叶片移动,外侧为海水介质,由于颗粒与导叶壁面碰撞摩擦,颗粒速度逐渐减小。 小颗粒呈现多层连续滑移,大颗粒则多以单层和离散滑移为主。

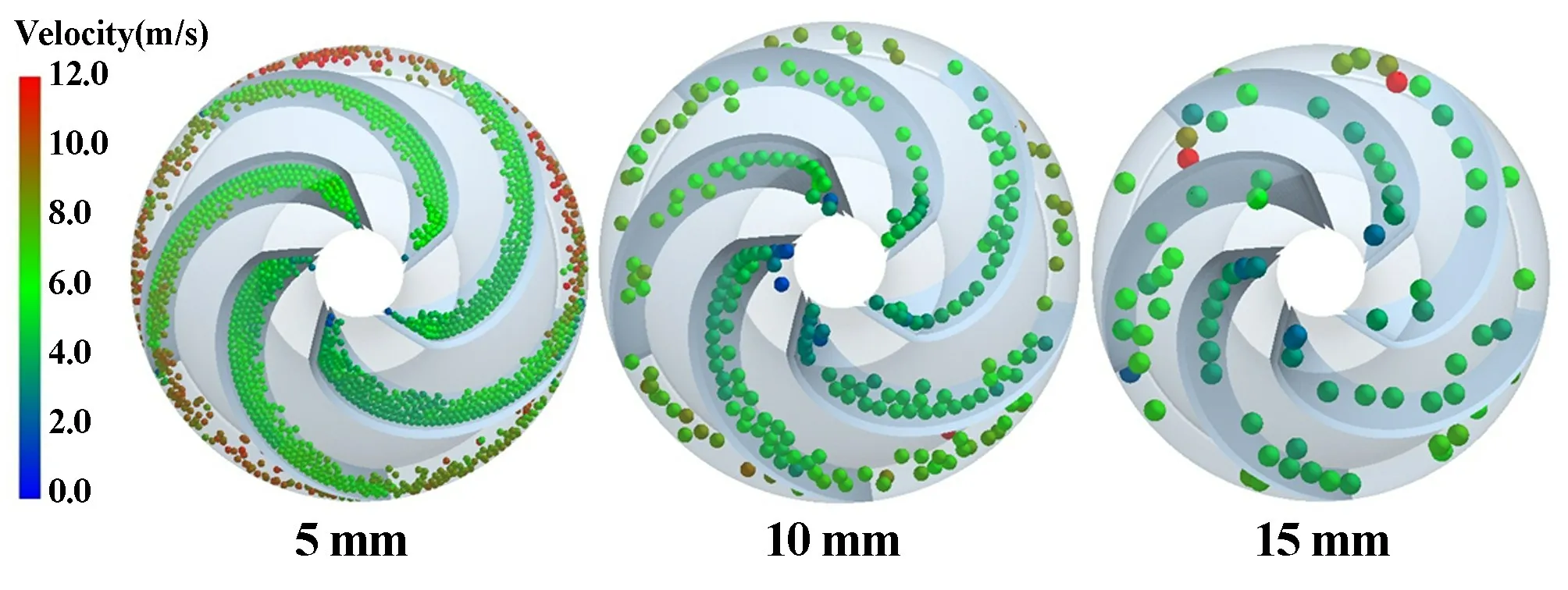
图7 导叶内颗粒的空间分布

颗粒由导叶以较高速度进入出口延长段,颗粒的速度由于重力和清水的“阻尼”作用,将会逐渐减小,5 mm,10 mm 和15 mm 粒径颗粒在出口延长段的速度分别为3.22 m/s,3.12 m/s 和3.05 m/s,均高于出口延长段清水的速度(2.89 m/s)。

2.3 不同颗粒粒径对流场的影响

为了研究不同粒径颗粒的运动对叶轮和导叶流道内流场的影响,监测叶轮和导叶流道中间位置处的流动参数进行分析,同时为详尽阐述流动机理,特选择5 mm 的流场,将叶轮按照叶栅周向展开,对比说明叶栅内的流动特征。

2.3.1 叶轮内的流场特性

图8 为不同粒径下的叶轮流道内速度和压力变化曲线,右侧云图为相对应的叶栅内流动特征(下同)。不同粒径的颗粒在叶轮流道内流体速度呈现相似的变化趋势,存在两个显著的拐点,出口速度比之进口有一定增加。 实际上,离心泵的叶轮过流面积是逐渐增大的,因此理论上单相介质在流道内的流速是减小的,造成速度波动的主要原因是流道几何和局部流动扩散。 图中2 点位置为叶片进口,由于叶片排挤作用,流速增大,从2 点到5 点流速的下降主要是流道的扩散,5 点以后到出口的流速增加主要是局部的低速区和流动分离引起的,将图8 的流线分布与图6 比对,可知颗粒在工作面附近聚集,形成局部低速区,流体则在外侧加速通过。

图9为3 种颗粒作用下的流体在叶轮流道内的静压分布,总体而言其压力特征为叶片核心区域压力均匀上升,后段(5 点以后)出现下降和波折,压力下降的原因主要是流速增加,而压力拐点出现在6 点位置处,既与出口截面积扩散有关,也与流道中后部的漩涡有关,漩涡引起的不稳定流一定程度上降低了流动的效率。 位置5 点以后小颗粒流体的压力略高于大颗粒,表明小颗粒群从叶片获取能量的能力略高于大颗粒,进一步被加速的颗粒又因速度滑移和流固黏性力的作用,将一部分动能转化为流体的能量。

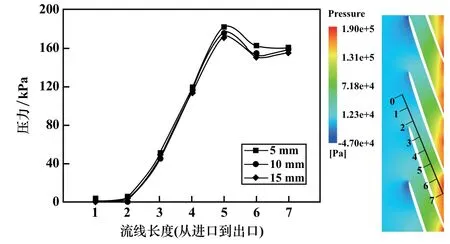
图9 叶轮流道内流线方向上的压力变化

2.3.2 导叶内的流场特性

图10 为导叶内的流场特性,流速整体下降,导叶流道内出现了显著的涡旋,从进口稍后位置一直延伸到中后部,不同流道流动特征存在较大差异。 相对于叶轮内叶片的持续做功,导叶内流体是一个动量矩守恒的动压和静压转化的过程,因此理论上单相介质在导叶内的能量变化特性应该是降速增压的过程。 实际由于设计阶段颗粒过流的考虑,将导叶过流截面做了较大的修正,同时颗粒两相的内部耗散导致静压出现了一定的下降。 此外,粒径的差异也引起了速度下降快慢的变化,10 mm 的颗粒流场流速下降相对均匀,15 mm 颗粒流场流速前段后段均下降较快,5 mm 颗粒流场流速前段平缓后段陡降,拐点位置出现在11～13 点处。

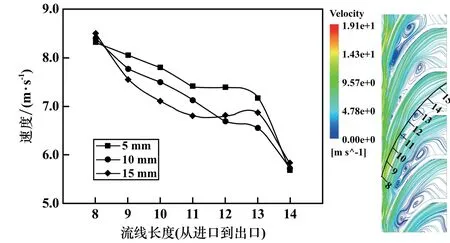
图10 导叶内流线方向上的速度变化

导叶内流线方向上的压力变化见图11。 可见导叶内的压力变化特征与流速相类似,整体下降,10 mm颗粒的变化幅度小于5 mm 和15 mm 颗粒。 压力云图出现了一定的局部高压区,与拐点区域相对应,此外静压的周向梯度显著,压力面显著高于流道中间和吸力面区域,证实颗粒两相的流动分离。

图11 导叶内流线方向上的压力变化

2.3.3 叶轮-导叶级间流场特性

深海采矿矿浆泵的单级水力包含动叶栅和静叶栅,二者的动静耦合往往伴随着能量损失和流动不稳定。 叶轮-导叶级间流场特性见图12。 由图12(a)可知,叶轮导叶衔接处为局部高速区,无论是叶轮段还是导叶段,该处均存在显著的周向速度梯度,吸力面一侧高速,压力面低速,导叶进口后端的压力面一侧漩涡明显。 图12(b)显示,二者过渡区域总压变化频繁,导叶内的总压梯度并不是呈现流动方向,径向的总压梯度显示了固液流动的分层和周向压力面一侧流动的不稳定。 即颗粒对于流动的影响更多地体现在周向的分层(或者过流断面流动特征),而非流线方向。

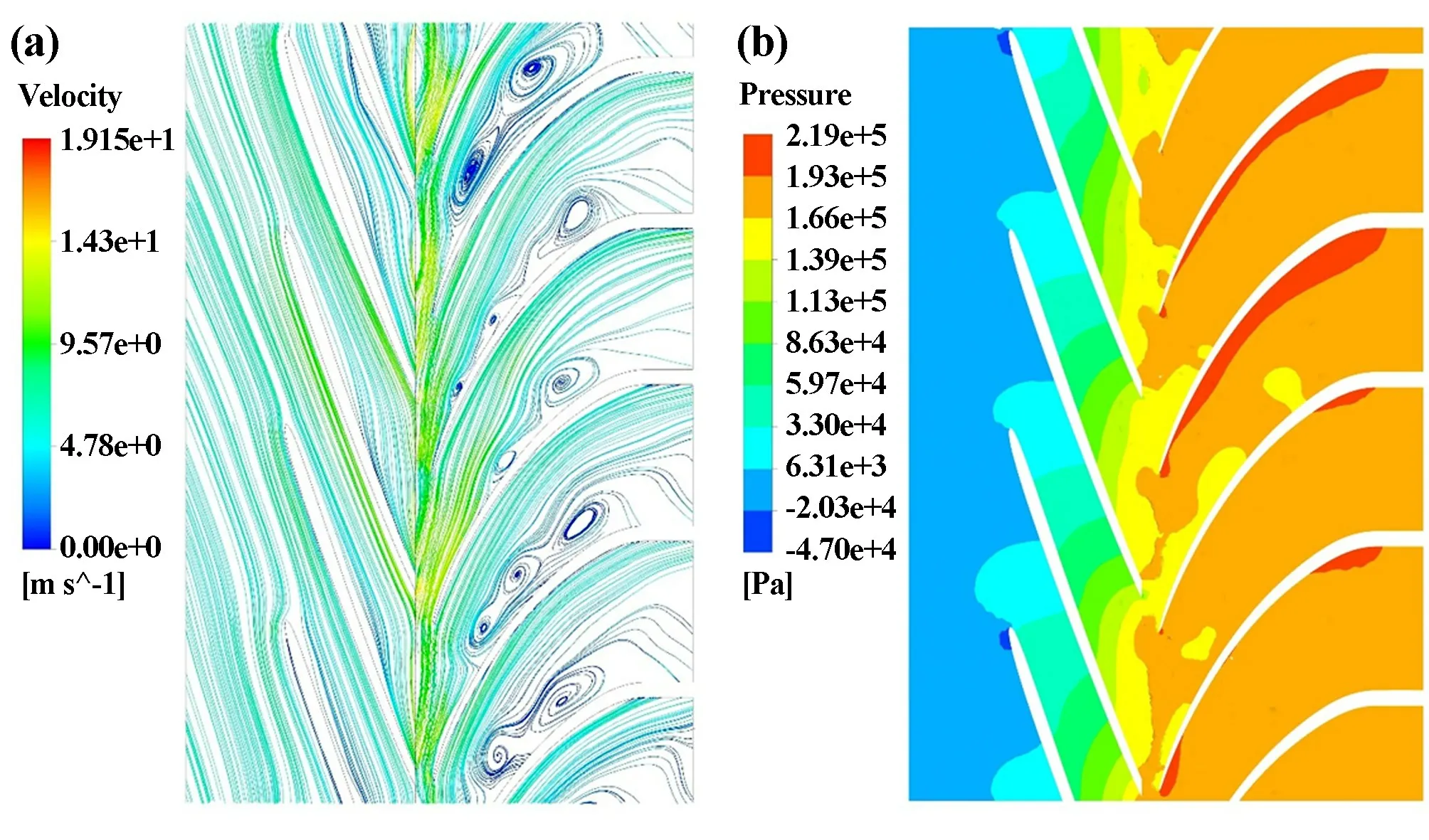
图12 叶轮-导叶级间流场特性

3 数值计算验证

为验证数值计算的可靠性,搭建如图13 所示的矿浆模型泵试验系统。 试验时通过调节阀门开度来控制泵出口压力,获得泵矿浆工作特性。 测试系统包含泵进出口的压力变送器、管线流量计、转速转矩仪等传感器、信号采集和数据处理系统等,所有的传感器误差均在3%以内,保证试验数据的准确。

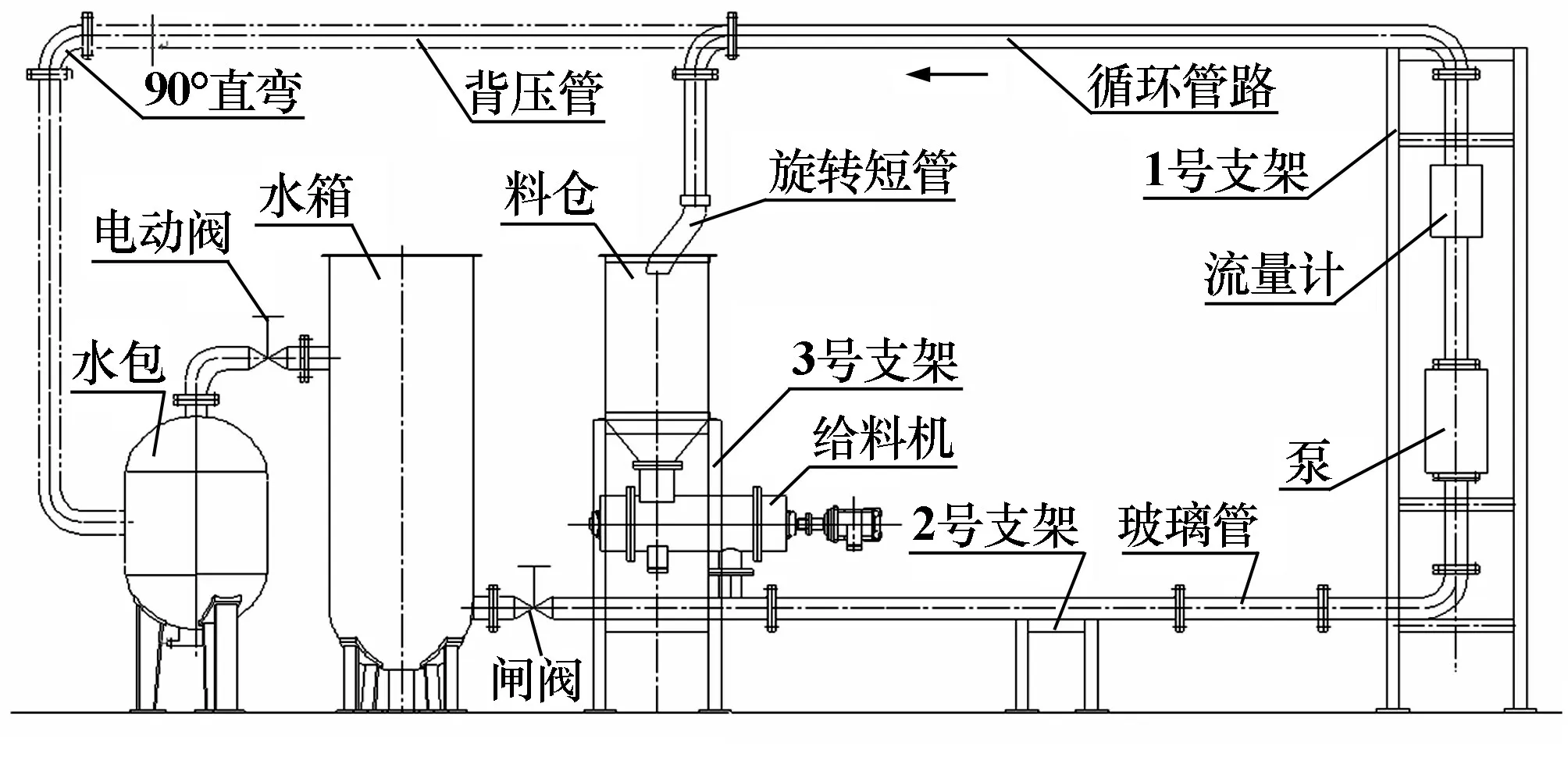
图13 浆料输送系统示意

考虑到模型泵的两级和泄漏效应,参照经验公式对数值计算的结果进行修正［11］(修正系数0.96～0.98),最终数值计算的泵扬程和效率数值与试验对比数据如表5 所示。 扬程和效率的数值模拟相对误差均在5%以内,表明数值模拟结果较准确。 矿浆泵输送浆料时的扬程和效率均低于清水工况,且扬程和效率随颗粒粒径增大而下降,这与清水和颗粒之间速度差异而导致的水力损失有关。 清水和颗粒的密度差导致的颗粒“沉降”效应,颗粒与颗粒间的碰撞以及颗粒和清水在与泵内壁面作用时表现出不同性能等原因均会形成两者的速度差,且颗粒粒径越大,速度差越大,由于液体“阻尼”,能量会有损耗,造成泵扬程和效率下降。

表5 数值计算与试验结果对比

4 结 论

1) 基于离散元方法的CFD-DEM 耦合策略能较为准确地计算大颗粒固液两相介质在离心泵内的复杂流动问题,计算结果与经验公式计算结果吻合较好。

2) 颗粒在泵流道内产生局部聚集效应,叶轮和导叶内的颗粒体积浓度均高于管线平均值,且颗粒粒径越大,局部体积浓度越高。 颗粒和流体在叶轮和导叶内呈现显著的分层运动,在叶轮内贴近压力面滑移,而在导叶内则偏向吸力面。 小颗粒获得的能量特性优于大颗粒。

3) 颗粒的存在导致了流动分离和流道漩涡存在,过流面积的扩散和固液两相的内部损耗是流道内能量损失的主要原因。 随着粒径增大,矿浆泵性能下降。

4) 本文研究结果可为大颗粒固液两相流的计算和深海采矿矿浆泵的优化设计提供理论指导。