匹配市场算法


匹配,是人们社会生活中许多问题的一种抽象。例如高考录取,是考生与大学之间的匹配;学生毕业了找工作,是毕业生和用人单位之间的匹配;男女婚恋,自然也是一种匹配。这些匹配的形成过程,常常会在某种制度(包括法律法规、约定俗成的做法等)下进行。显然,这些匹配的结果如何(与制度很有关系),具有重大的社会意义。于是,匹配的制度设计就成为一个很有价值的问题。2012年诺贝尔经济学奖,就颁发给了两位在这方面作出突出贡献的学者。
匹配市场模型
上面这些例子的共性,一是有双方,每一方有多个对象,二是互选,事情不能一厢情愿,纠结就发生在这里。其实,即便不是互选,由于资源有限,常常也会很难搞定。想一想那些热门的大学吧,就算大学不挑学生,但宿舍床位有限,食堂空间有限,不可能容纳所有希望去的学生,最后总有一个怎么安排的问题。
下面我们来讨论一种相对单纯点的匹配问题,看看算法思想如何在其中发挥作用。设想有这样一个情境:你有A、B、C、D有一定价值的4件旧物品希望送出去,现在有4个人W、X、Y、Z有兴趣要。当然,一人分得一件是比较合适的,也就是说要在物品和人之间形成一个匹配。可物品是不一样的,某两个人可能最想得到某同一件物品,该如何安排呢?
按照经济学的语言,这意味着需求和供给之间有冲突。尽管你只是想把物品送出去,并没有想赚钱,但我们不妨从市场的观点来探讨一种解决方案。你告诉他们,每人对每件物品给出一个以金额表达的价值,对应他愿意支付的最大数额以得到相应的东西,但超过了就不值了。这样,所表达的价值就反映了人们对不同物品的喜爱程度。假设他们告诉你了,于是你就面对如图1(a)所示的一个局面。
图1中的4×4数据矩阵就是W、X、Y、Z对A、B、C、D的估值。每一行对应一个人,每一列对应一件物品。从中我们看到W最喜欢的是B,因为他给出的估值是9,在第一行中最大。而X和Z最喜欢的都是A,因为都给出了最大估值,于是有冲突了。图1(b)与(a)含义是一样的,只是另外一种图示,便于后面的算法讨论。
怎么办呢?人们参照市场经济的一种基本精神——物以稀为贵——设计了一个算法。该算法要通过为物品确定一组价格,来达成某种最优意义下的物品分配。下面先就图1的例子,通过图2中的三个图来解释这个算法的步骤,接着再讨论它的一些性质。
先看图2(a),它和图1不同的是左边添加了4个0,用以表示A、B、C、D的初始尝试价格。同时我们也注意到,在原先的物品(A、B、C、D)和人(W、X、Y、Z)之间添加了一些边(线),形成了一个二部图,也就是节点可以分成左右两边,边只是跨两边节点的图。在这个算法中,那些边的含义很关键,表示“最大差价”。例如,W和B之间的边,意味着9-0=9是W目前看到的最合适的物品,于是表达了“W最希望得到B”的含义。此时,初始价格为0,最大差价也就对应最大价值了。若价格变了,最大差价自当改变,于是二部图中的边也就要相应调整了。
下面来重点了。我们看到图2(a)中表现出了一些冲突。例如,从W、X、Z沿着边向左看过去,只能看见A和B。也就是说三个人表达的最爱集中在两个物品上,因此没法都照顾到!怎么办?物以稀为贵,让那些供不应求的物品加点价!于是我们看到了图2(b),其中A和B的价格提升到了1。这里的算法规则是让二部图中的边总是对应最大差价。不过,就这个例子的当前数据而言,边还是那些,因此二部图的样子没有变。
下面是另一个要点。可以看到图2(b)中依然有W、X、Z三个“争抢”A和B两个的现象。我们可以继续给A、B加价。不过,还可以看到X和Z要的都是A,也是一种“供不应求”现象,于是也可以就单给A加价。这里是想说,加价的方式不唯一,只要是针对“供不应求”现象都可以。不同的选择不会影响最后结果的性质(可能对效率有些影响,但不是本文重点)。假设我们现在就选择只给A加价。
现在看图2(c),A的价格提升到了2。我们看到,按照“最大差价”原则确定的物品和人之间的边,二部图发生了一个关键性变化——X现在认为也可以要D了,A和D对他来说差价都是6。于是,就浮现出一种无冲突安排,也叫完美匹配:A—Z,B—W,C—Y,D—X。
这样一种安排意义重大。首先,每个人得到的都是对他而言差价最大的物品,也就是说他不可能通过要求换一个物品来获得更大的差价。再者,如果我们看4件物品对于它们的获得者的价值,对应图2(c)右边估值矩阵上圈出来的4个数字,满足一个令人兴奋的性质:它们的和是该矩阵上不同行不同列元素之和的最大值。这意味着,尽管并不是每个人都得到了最初最想要的物品(如X没有得到A),但这种分配实现了一种总体价值最优,称为达到了社会最优。
匹配市场算法
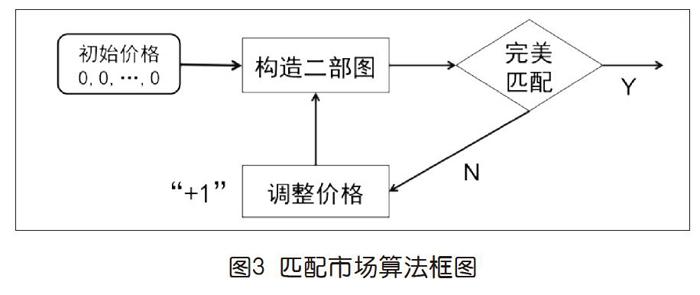
上面的例子,让我们看到了借助市场“无形之手”——通过价格调整供需关系——得到的一种匹配的算法。一般地,给定任何非负整数估值矩阵,图3所示即为这个算法的框图。
一共有四個框,其中“初始价格”框没什么说的。
“完美匹配”是判断在二部图上是否出现了无冲突的匹配关系。图论告诉我们,如果没有完美匹配,就意味着存在那种供不应求的冲突情况,也称为存在受限组,即二部图一边的节点子集,大于邻居节点集。
如果发现了在“人”一边存在一个受限组和它对应的“物品”集合,“调整价格”就是很简单的事情,即给那些物品的价格+1。在前面的例子中已经提到,在任何受限组基础上做这种价格调整都会得到一致的结果。
而基于当前价格按照最大差价原则重新“构造二部图”,确定该有哪些边,也是直截了当的,即后面讨论中会看到的。其中,取得max的k(可能多个)就指示“人”节点i就和“物”节点k之间有一条边。
难点在哪里?在于如何判断一个二部图中是否存在一个完美匹配。对于图2所示的例子,规模很小,我们凭目测就可以断定(a)和(b)中没有完美匹配,(c)就有了。但一般来说这是不容易的。体会一下这个难度,请看图4。其中展示了四个二部图,你能看出哪些有完美匹配吗?如果没有,能指出一个受限组吗?
也许,你目测能力很强,看到(a)中不存在完美匹配,因为有受限组{a,b,c,e},它们对应到左边只有{1,3,6};还能看到(c)中存在完美匹配a—4,b—1,c—3,d—2,e—6和f—5。但你肯定感到了这是一个相当困难的任务,需要用计算机来解决。的确,为了使图3所示的框架性算法能够实现,在“完美匹配”判断框要启用一个子算法,相当于调用子程序。
有多种不同的方法来判断一个二部图是否存在完美匹配。其中之一,就是利用本栏目在2020年8月刊上介绍的求网络最大流的算法。下面,就来看网络流问题和这里的匹配问题是怎么联系起来的。
回顾网络最大流问题。它针对一个有源节点(s)和目标节点(t)的加权有向图,确定从源到目标能够实现的最大流量。下面我们会看到,有一种相当直接的方式,将判断两边都有n个节点二部图是否存在完美匹配的问题实例转换为一个网络最大流问题的实例,以至于后者的最大流量达到n,当且仅当前者存在一个完美匹配。
我们用如上页图5中的例子来解释这个对应关系。(a)是要判断是否存在完美匹配的二部图,(b)是一个网络最大流问题的实例。它基于(a),添加了两个节点s和t,s连到右边所有节点,t连到左边所有节点;给所有边赋予从右向左的方向,且令每条边的权值均为1。
不难看到,如果图5(b)中s到t的最大流量达到了n,注意到每条边的权重均为1,就意味着从s到t有n条中间节点无重用的路径,也就是(a)中有完美匹配,对应那些从s到t路径中的中间边。反之,如果(b)中s到t的最大流量小于n,意味着(a)中不存在n条端节点无冲突的边跨接在左右两边,也就是没有完美匹配了。此时,记L和R为二部图中实现最大流的左、右两边的节点集合,受限组就是R加上右边任一其他节点,在匹配市场算法中需要加价的就是L中的节点。以图5(b)为例,能发现从s到t的最大流量是5,具体实现为s→a→1→t,s→b→3→t,s→c→6→t,s→d→2→t,s→f→4→t,小于节点数6,因而二部图5(a)中不存在完美匹配,需要给节点1,2,3,4,6加价。
上述这一段讨论有特别意义。当算法学习积累到一定程度,面对新的问题,往往有可能借用先前针对不同问题的算法。此时,关键在于要能在两个问题之间做适当的“映射”,能够从对老问题的解中“解释”出对新问题的解来。
匹配市场算法的性质
至此,对图3描述的匹配算法还能提什么问题吗?至少还可以问两个问题。第一,在調整价格的时候为什么总是“+1”?一次多加点会不会效率高一些?例如,从图2(a)到图2(b)似乎没起任何作用,如果一次性加2,就会省下一轮迭代。第二,算法是以完美匹配的形成作为终止条件的,为什么一定会形成呢?
这两个问题其实有关联。看图6所示n=2的小例子,调整价格的时候做“+2”,会出现什么现象。
可以看到,调整价格时做“+2”,整个情形就会在两种状态下无限循环往复,形成不了具有完美匹配的二部图。下面就来证明,“+1”则会保证具有完美匹配二部图的形成,即该算法一定会结束。
一般而言,算法是作用在某些数据上的处理过程。那些数据会在这个过程中得到某些改变。为了证明一个算法过程一定结束,尤其是对一些“框架性算法”(其结束条件可能是比较高层次的描述,就像这里的“出现了具有完美匹配的二部图”),一种很有用的方法是选择适当的数据对象,证明在算法过程中其值是单调有界的。这种方法本栏目在2020年8月刊讨论网络最大流算法时就用过。当时的结束条件是“不再有从s到t的增量路径”,我们选取的数据对象是从s出发的剩余容量总和。
对本文讨论的匹配市场算法,涉及的量包括估值矩阵中的值(在算法过程中不变)和在过程中变化的价格(初始为0)。为方便讨论起见,用V来表示估值矩阵,a表示动态调整的价格向量,如图7所示。
我们基于它们构造一个数据对象P如下。它包括两个求和项,第二项是当前价格之和,第一项对应当前价格下的最大差价之和。下面来证明P在算法执行过程中具有“单调减且有下界”的性质。
在理解了算法操作的基础上这个证明不难。由于“+1”涉及至少一个物品,第二项在算法的每一轮一定是递增的,如果涉及了m个物品,也就是增加了m。对应到二部图中的受限组,则至少涉及m+1个人,也就是在第一项中至少有m+1个max会减少1。减的多增的少,整个就是单调减了。如果是“+2”,第二项将增2m,但就不能保证第一项减量超过2m了。请读者思考为什么。
为什么有下界呢?只要注意到V是给定不变的和下面的推导式就可以了,其中不等号是取k=i所致。
好了,到这里基本就完成了关于一个重要的匹配市场算法的讨论。值得问的一个问题是,算法过程并没有直接针对要获得匹配估值总和的最大值,它只管按照物以稀为贵的原则调整价格,人们按照自己的估值和当前价格做对自己最有利的诉求表达(二部图中以最大差价为指示的边),但“无意中的”结果就是社会最优。这是必然的吗?答案是肯定的。这个模型可以看成是对“无形之手”理论的一种非平凡的具体诠释。
参考文献
[1]David Easley, Jon Kleinberg.网络、群体与市场[M].李晓明,等,译.北京:清华大学出版社,2011,10:175-185.
[2]李晓明.网络流问题[J].中国信息技术教育,2020(15-16):16-21.
注:作者系北京大学计算机系原系主任。

