基于分形维数的正则化图像复原方法

王亚云

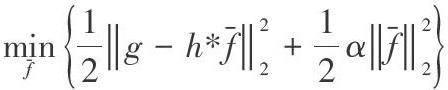
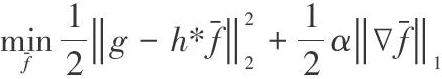
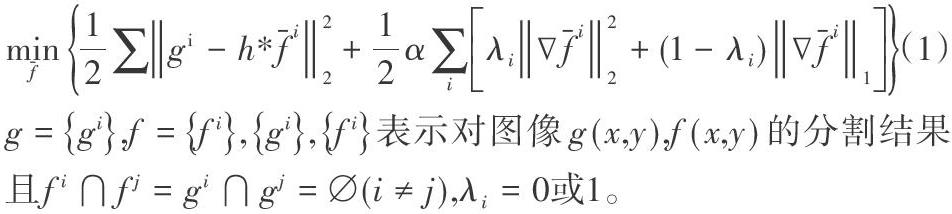
摘要：正则化方法是指在空间域上以符合图像特征的先验信息作为约束条件，寻找与模糊图像最近似的清晰图像以作为解的一种图像复原算法。本文研究正则项的泛函形式，基于单一全局泛函的不足，将图像空间看作微分流形，以图像分形维数为特征进行分类，进而对不同区域采取不同的泛函约束，得到正则化模型。仿真实验表明，该方法比单一范数形式复原效果更佳。

关键词：图像复原;正则化;微分流形;分形维数

中图分类号： TP391        文献标识码：A

文章编号：1009-3044（2021）02-0166-03

Abstract： The regularization method in image restoration area is a means for obtaining the restored image that approximate to the damaged image by setting the regulation term with a novel prior assumption within the image space. Due to the defect of the traditional single assumption， we can take the image space as a manifold. The feature can be identified by fractal dimension so that the images can be classified. Then the model can decide the form of the regularization term by using the different prior assumptions. It is verified that the new model achieves the desired results.

Key words： image restoration; regularization; manifold; fractal dimension

图像在形成、传输和存储等过程中因退化因素如模糊、噪声等形成降质图像。图像复原即为根据降质图像寻找清晰图像的过程。实际应用中，图像复原是指依据图像退化的先验知识及降质图像信息，建立图像退化模型进而求解[1]。近几十年中，图像复原方法大致分为基于滤波的算法、基于统计模型的算法及正则化算法。由于对模糊、噪声成因缺少先验知识，图像复原问题往往复杂且具有不适定性，即不满足解的存在性、唯一性及稳定性。自Tikihonov提出正则化方法以来，不适定性问题获得了有效的修正方法。正则化方法是指在空间域上以符合图像特征的先验信息作为约束条件，寻找与模糊图像最近似的清晰图像以作为解。图像的先验信息在模型中以正则项的形式出现。因此，正则化项的选取对于复原效果具有重要意义。

正则化项若取为L2范数，则能较好平滑图像中的噪声，但易丢失图像的边缘细节，而L1范数能保留边缘细节，但在平滑区域易造成“分片常数”的现象。因此，考虑在不同特征的图像区域借助图像在流形上的特点构造不同的正则化项，建立图像复原模型。

1 图像复原及正则化方法

图像的模糊在数学描述上体现为卷积，噪声则具备统计特征，一般服从正态分布。通常情况下，图像的退化过程最简单的模型如下：

对上述模型进行最小二乘估计，求解得出：

分析可知，该问题的解存在不适定性。通过在目标函数中添加正则项，引入关于真实解的先验信息约束，可稳定该问题的解，这种方法即为正则化方法。由此，得到修正后的正则化模型：

其中，第一项为保真项，表示原始图像模糊后与观测图像距离，主要用于抑制噪声;第二项为正则项，a为正则化参数，用以平衡保真项和正则项，进而影响图像复原效果。正则化项的确定是正则化方法的关键。如Tikhonov正则化[2]选取原图像的二次函数作为正则化项，以限制解为平滑解，抑制噪声。其模型为：

该模型对于实际问题中存在大量边缘纹理细节的图像复原时因平滑解而使得复原图像丢失大量细节。

以Tikhonov正则化为代表的二次型正则化模型通过构造二次正则项获取平滑解，因此非二次型正则化项可以解除平滑性约束、保留图像边缘纹理细节。其中，最具代表性的是全变差（TV）模型[3]：

总体上说，对于正则化项的优化主要體现在两方面：（1）正则化项中高通滤波器（如梯度算子等）的选择，以区分图像的边缘和高频振荡成分;（2）正则化项中能量泛函的范数形式的确定。

2 流形正则化算法

2.1 流形正则化模型

正则化方法一般对图像整体采用统一能量泛函形式。基于对泛函形式的分析，对于一副包含大量边缘轮廓信息的图像来说，Tikhonov正则化模型求解的效果显然不如TV模型，反之，对于“分片常数”的图像，后者复原效果不如前者。考虑一个图像不同部分可能具备不同特征，进而使用不同的泛函形式，以平衡平滑图像噪声和保持图像纹理特征这一对矛盾。

受文献[4][5]启发，将图像空间看成“流形”，对局部图像块进行特征的确定进而决定其在流形中的位置，根据位置的不同采用不同的能量泛函形式，即为“流形”正则化方法。为方便讨论，将图像分为两类，分片常数类和边缘纹理特征明显类，进而正则化项泛函形式二分为L1形式及L2形式。为区分这两类图像，考虑图像块的分形维数作为特征。由此得到流形正则化模型：

2.2 分形维数

分形理论是现代数学与非线性科学研究中新兴分支。分形维数是分形特征的定量描述。自然界大多数表面在空间上都是分形的，其映射成的灰度图像是具有相同分形特征的表面，且分形维数越大，图像表面越粗糙，维数越小越光滑[6]。因此考虑用分形维数描述图像纹理粗糙程度。规则分型常以Hausdorff维数作为分形维数，不规则分型维数计算方法种类较多，本文选取差分盒子维方法计算[5]。

一副图像的分形维数值介于2.0-3.0之间，图像平滑区分形维数接近2，纹理区接近3。选取测试图像如图1所示。

分别选取平滑区域1、纹理区域2，根据差分盒子维方法，计算得出区域1分形维数为2.000，区域2分形维数为2.585。对于区域1使用L2范数有利于去噪，区域2使用L1范数保留纹理特征，即根据第i块区域的分形维数Di确定[λi]取值。为此，定义：

实验中，为实现全体像素的分类，须估算每一个像素点的分形维数。为此，将256*256大小的图像分为16*16小块，每一块像素为16*16，计算出每一子块的分形维数，利用线性插值，估算各像素点分形维数。图2显示了利用分形维数对图像house、lake中不同特征图像子块的分类结果。可见，分形维数对于平滑区域和纹理区域的分类较为清晰。

2.3 变分梯度流模型

确定参数[λi]后，利用变分法得到流形正则化模型的梯度流方程：

根据假设，各图像块互不相交，故每个图像块上扩散方程为：

由变分法，得上式对应的偏微分方程形式为：

2.4 模型求解

利用上式近似求解时，将[λi]取值相同的子图像块合并为大图像块，接着在大图像块上进行扩散。因此，[λi]与图像块[fi]交叉变化，设计算法如下：

（1） 初始化：实验中，对大小为256*256的图像分割为16*16的小块，计算出各图像块的[λi]值，将取值为0、1的子块分别合并成大图像块;

（2） 在大图像块上，利用（5）式进行迭代，得到扩散结果[fi];

（3） 根据（2）中更新的[fi]重新计算每个子块的[λi]值，重复步骤（1）;

（4） 交叉进行（2）（3），直到迭代稳定为止。

3 实验结果及分析

考虑高斯模糊，点扩散函数为：[k（x，y）=e-x2+y22σ2]，将点扩散函数离散为[[-3σ，3σ]2]矩阵并进行归一化处理。在matlab2018a环境下，首先将原始图像灰度值归一化处理，计算高斯函数与原始图像的卷积，接着给模糊图像附加方差为0.01的高斯白噪声。

针对下列两个测试图像图像，分别使用L1泛函、L2泛函及流形化模型泛函，结果如图3所示。

从图像中可以看出，流形正则化方法在去噪方面不如L1范数形式，在避免“分片常数”效应方面有优势，图像子块的均获得较好复原;与L2范数形式相比，流形正则化保留了更多的边缘纹理细节。

引入评价指标MSE、PSNR对house、lake两幅图像复原效果进行比较评价，其中：

计算结果如下：

4 小结

本文基于正则化项范数形式对于图像复原效果的影响以及将图像视为非欧几何中的微分流形的观点，基于图像内蕴几何性质—分形维数为特征，在图像流形上建立不同形式的泛函形式，得到相应正则化模型。以house、lake为实验对象，比较不同泛函形式下图像复原效果，图像直观以及峰值信噪比PSNR客观取值均表明，该模型比单一范数约束复原效果更佳。

参考文献：

[1] 张彬，于欣妍，朱永贵.图像复原优化算法[M].北京：国防工业出版社，2018.

[2] Tikhonov A N. On the solution of ill-posed problems and the method of regularition[J]. Soviet Mathematics，1963（4）：1035-1038

[3] Umut Guclu，Yagmur Gucluturk，Chu kiong Loo. Evaluation of fractal dimension estimation methods for feature extraction in motor imagery based brain computer interface[J]. Procedia Computer Science，2011，3：589-594

[4] 于欣妍，王亮，罗四维.基于微分流形的图像复原方法方法[J].北京交通大学学报，2015，5（39）：1-7.

[5] 金文清.基于微分流形的图像处理和算法研究[D].南京：南京理工大学，2015.

[6] 赵莹，高隽，陈果，冯文刚.一种基于分形理论的多尺度纹理特征提取方法[J].儀器仪表学报，2008，4（29）：177-781.

[7] 王迪吉.基于分形维数的纹理特征的提取与应用[J].石河子大学学报（自然科学版），2007，5（25）：650-653.

[8] 赵海英，杨光俊，徐正光.图像分形维数计算方法的比较.计算机系统应用，2010，20（3）：238-246.

【通联编辑：唐一东】