适用于西藏地区的聚风型垂直轴风力机结构特性分析

赵斌，武熠杰，王绍龙，袁喜鹏，冯放

(1. 华北理工大学冶金与能源学院，河北 唐山 063210； 2. 长沙理工大学能源与动力工程学院，湖南 长沙 410114； 3. 西藏自治区能源研究示范中心，西藏 拉萨 850000； 4. 东北农业大学理学院，黑龙江 哈尔滨 150030)

西藏自治区不仅太阳能资源丰富，年辐射量居中国首位，且大部分地区属于风能可利用区域，西藏风能资源储量居中国第七，那曲和阿里部分地区年平均风速可高达4.3 m/s，风能密度大于500 W/m2，因而在西藏地区开发利用风能和太阳能资源具有十分广阔的前景[1].太阳能与风能存在间歇性和时段上互补性的特点，因此在阿里和那曲等高海拔偏远地区建设风光互补分布式电站，不但可丰富西藏电源结构，同时还可促进当地清洁能源产业的发展，满足当地用户的用电需求[2].

西藏地区风能资源丰富区多位于西藏地区中的高寒高海拔领域，虽然瞬时风速高，但风向多变，最突出的问题是空气密度低，仅为内陆低海拔地区的0.6左右[3].因此，若要在西藏发展风力发电，需充分考虑以上特点.由于空气密度低导致常规风力机不能达到在内陆地区的额定功率，通常的解决办法是增大风轮尺寸.然而，西藏地区由于高海拔，施工建设非常艰难，大型风力机并不适合.同时，风向多变的特点使得相比水平轴风力机而言，垂直轴风力机更适合西藏地区.基于这些因素，开发了适用于西藏地区的聚风型直线翼垂直轴风力机[4]，借助聚风装置提升风轮入流风速和能量密度.前期的数值模拟和风洞试验表明在不增加风轮尺寸的条件下，风力机的气动特性大幅提升，可以用于西藏地区.然而，由于西藏地区的地理和气候特点，建设施工和维修维护成本非常高，这对风力机的结构、强度和可靠性等方面提出了更高的要求.因此，需在风力机安装之前，对聚风型直线翼垂直轴风力机的结构进行计算分析.

国内外关于垂直轴风力机的结构设计与分析研究较少，苏永清等[5]提出一种基于振动速度补偿反馈的PID风机独立变桨控制方法，该方法不仅能够保障风力机稳定输出功率，也可以有效减小了桨叶的振动速度及振动位移差，从而减小了桨叶对风力机塔身造成的疲劳载荷，提高了风力机运行的可靠性，延长了风力机的使用寿命.FENG等[6]设计了一种升阻复合型垂直轴风力机，并通过ANSYS有限元进行静力学和动力学分析验证了其结构的可靠性，为风力机结构设计提供了参考.然而，对于聚风型垂直轴风力机的结构特性分析还未见报道.

文中在前期研究的基础上，以面向西藏地区应用的额定功率为500 W的聚风型直线翼垂直轴风力机为对象，以高寒高海拔地区的气象参数为约束条件，对风力机进行静力学分析和整机模态分析，以确保该型风力机强度满足要求，运行安全可靠.研究结果可为聚风型直线翼垂直轴风力机在西藏高寒高海拔地区的应用提供理论基础.

1 风力机基本结构

1.1 三维模型

聚风型直线翼垂直轴风力机风轮上下两端各加装了B样条曲线结构圆台型聚风罩，再配装发电机、支撑臂、法兰、支柱等部件，安装于柱形塔筒上，组成风力机模型.风力机模型如图1所示.

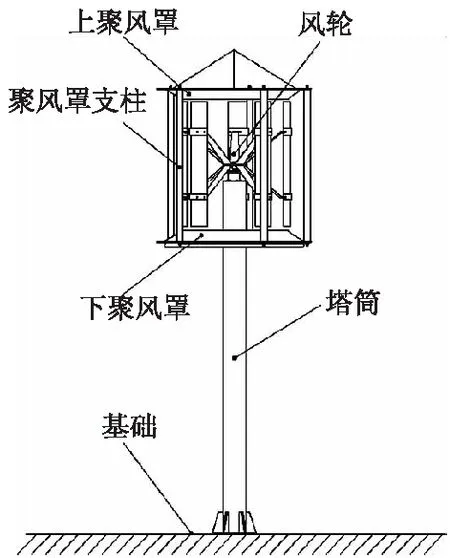
图1 聚风型直线翼垂直轴风力机模型

1.2 基本参数

500 W聚风型直线翼垂直轴风力机主要结构部件指风轮叶片、支撑臂、法兰盘、主轴、聚风罩和塔筒.在风轮气动设计的基础上，需设计满足结构力学特性要求的结构部件，连接支撑整个风轮，确保风轮安全稳定运行[7-8].依据经验[6]和风力机安装地区的气象条件，该型风轮气动参数及主要部件结构参数选取：额定功率P=500 W，额定风速v=12 m/s，额定转速n=150 r/min，风轮直径d=1 400 mm，叶片数目N=5 个，叶片弦长c=225 mm，叶片翼型为NACA非对称翼型，叶片高度hb=1 600 mm，叶片质量mb=4.76 kg，支撑臂质量mbeam=5.8 kg，主轴质量ma=1.0 kg，法兰盘质量mfp=10.0 kg，聚风罩数目Nwgd=2 个，聚风罩高度hwgd=150 mm，聚风罩线型为B样条，上聚风罩质量mup,wgd=32.5 kg，下聚风罩质量mdown,wgd=31.8 kg，塔筒质量mt=365.0 kg.

HAMEED等[9]通过研究发现叶片主要受到离心力载荷作用会产生较大的弯曲变形.由于玻璃钢材料具有质量轻、机械强度高和耐腐蚀等优点，该风力机选用玻璃钢叶片材料.为保证强度和硬度，同时减轻叶片质量，将叶片内部掏空，在内部设置2个腹板，起支撑加固作用.

风轮支撑臂一端与法兰盘固定，另一端用于固定安装叶片，由于叶片在运行中将对支撑臂产生较大的离心力，受力情况复杂，且支撑臂又是固定叶片的重要媒介，其高抗拉、抗压强度要求就显得尤为重要.因此支撑臂材质采用Q235钢板折弯对合，保证其强度和刚度.

主轴下端连接机舱，上端连接用于固定横梁的法兰盘，材质选用40Cr，并设计为锥形结构.

法兰盘与主轴通过键槽固定，主要起到固定支撑臂，连接支撑臂与主轴的作用，材质选用Q235厚钢板.

聚风罩是聚风型直线翼垂直轴风力机的重要部件，为保证其实现获得更多风能的要求，其内侧导流面需要严格符合B样条曲线，且不能大幅增加风轮质量，因此材质优选韧性好、质量轻、易造型的复合材料.下聚风罩和上聚风罩对向安装在塔筒法兰上，并通过5根支柱连接支撑，由于发电机及主轴安装位置的需要，下聚风罩需要开孔，因此上下聚风罩具有一定差异.聚风罩材料选用玻璃钢.结构模型示意如图2所示.

风力机塔筒起着支撑和固定机舱、风轮的作用.如果塔筒结构不够稳定会导致风轮无法正常工作，严重时甚至会引起风轮的脱落.由于无缝钢管制造而成的塔筒具有设计制造简单、性价比高、安装和维护便利等优点.因此，聚风型风力机塔筒根据经验采用壁厚8 mm Q235无缝钢管基材制造，通过焊接于底座法兰固定于地基上.

图2 聚风罩结构模型

2 力学特性分析方法

2.1 有限元法

首先需要对设计模型进行离散化处理，然后用形成的单元集合体来替代原有结构模型，再选用位移函数计算出单元体内的应力及应变，最后得到整个模型结构的平衡方程[10]，进而计算出模型应力和位移.

位移函数计算式为

u=Nδe，

(1)

式中：u为单元内任意一点的位移向量；N为形函数；δe为单元节点位移向量.

单元内节点应变和应力计算式为

ε=Bδe,

(2)

σ=Dε=DBδe=Sδe,

(3)

式中：σ为节点应力；ε为节点应变；B为应变矩阵；S为应力矩阵.

单元力学特性计算式为

Keδe=fe,

(4)

式中：Ke为单元刚度矩阵；fe为等效结点力.

整个结构的平衡方程为

Kδ=f.

(5)

在设定结构模型的边界条件下，利用式(5)即可解出该结构的位移δ，然后利用单元特性计算单元应力f.

2.2 载荷计算模型

风轮主要构件受到重力载荷计算式为

G=mg,

(6)

式中：G为主要构件重力，N；m为主要构件质量，kg；g为重力加速度，g=9.79 m/s2.

在额定转速下绕轴转动而产生离心力载荷计算式为

F=mrω2,

(7)

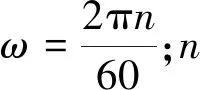
在额定风速下受到的气动载荷计算式[11]为

(8)

式中：p为气动载荷，Pa；ρ为空气密度，ρ取海拔5 000 m平均空气密度0.736 6 kg/m3；v为额定风速，12 m/s.

在额定功率下的转矩计算式为

(9)

式中：T为转矩，N·m；P为风轮额定输出功率，0.5 kW.

风轮水平轴向推力计算式[12]为

(10)

式中：F1为风轮水平轴向推力，N.

2.3 模态分析方法

风力机在自然风条件下运行时，受力情况复杂多变，叶片与来流相互作用会产生振动，使叶片出现疲劳问题，减损寿命，甚至可导致风力机叶片断裂飞出，发生损坏.文中通过模态分析，计算风轮振型和固有频率可确定风轮结构振动特性，在设计中避免叶片自振频率与风轮转速频率重合产生共振问题[13].

由结构动力学理论可知，整个结构的有限元动力方程[14]为

Ma+Cv+Ks=F(t),

(11)

式中：M为质量矩阵；a为加速度矢量；C为阻尼矩阵；v为速度矢量；K为刚度矩阵；s为位移矢量；F(t)为外力矢量.

当系统无外部约束或激振力时，则外力矢量为0，即F(t)=0.且工程分析结构固有属性时，通常忽略阻尼作用.将式(11)简化为

Ma+Ks=0,

(12)

解析式为

a=Xsinωt,

(13)

式中：X为振型；ω为固有频率；t为时间.

将式(13)代入式(12)得

(K-ω2M)X=0,

(14)

若令λ=ω2，使式(14)存在非零解，则

det(K-λM)=0,

(15)

解该特征方程式，即可得到n个特征值λi和模态形状X，将特征值λi求解即可得到多阶固有频率ωi.

3 静力学分析

3.1 叶 片

在ANSYS软件中的具体材料参数设置如表1所示，表中E为弹性模量，[δ]为屈服极限，A为许用应力.

表1 垂直轴风力机选用材料属性

叶片在转动过程中，主要受到叶片自身重力载荷，绕轴转动而产生的离心力载荷以及风吹过叶片而引起的气动载荷.额定转速下叶片的计算载荷:自身重力为46.6 N，离心力为821.3 N，气动载荷为53.0 Pa.

应用ANSYS有限元分析，在不改变结构模型特性的前提下，将结构模型进行简化，从而可有效提高计算速度.将叶片上的孔简化，网格划分类型选择四面体网格，设置最大网格尺寸以及对尺寸较小的面进行局部加密后自动生成网格，划分完网格后的叶片模型所具有211 623个单元，413 021个节点.在叶片与支撑臂连接孔处添加固定约束代表支撑；风吹过叶片而引起气动载荷，以压力载荷的形式施加于叶片迎风面；叶片自重，施加重力加速度；叶片离心力，以主轴为旋转轴施加惯性载荷里的旋转速度.额定转速运行下，叶片位移变形和应力分布如图3所示.

图3 叶片静力学分析云图

由图3a分析可知，叶片位移变形上下对称，最大位移变形产生在叶片叶尖处，最大位移为0.19 mm，叶片的变形趋势为叶尖部分位移变形最大，逐渐向内变小，直至叶片的固定孔处变为最小，后又向内逐渐变大，直至叶片中间部分达到一个较大值，该变形量对叶片的形状及气特性影响微小，因此满足设计要求；图3b分析可知，叶片的最大应力发生于叶片与支撑臂的连接孔处，最大应力为11.96 MPa，由连接孔向外，应力逐渐变小.

叶片强度校核公式为

(16)

式中：δmax为最大应力，MPa； [δ]为材料的屈服极限，450 MPa；S为安全系数，1.5.

计算可得，δmax=11.96 MPa<300.00 MPa，叶片所受到最大应力远远小于其能承受的最大应力.因此，叶片在额定转速下强度满足设计要求.

3.2 支撑臂

支撑臂在转动过程中，主要受到自身重力载荷、支撑臂绕轴转动而产生的离心力载荷、叶片重力对支撑臂造成的压力载荷、牵引于叶片离心力载荷的牵引力以及叶片转动而产生的转矩载荷.由于1个叶片由2个支撑臂共同承担，故单个支撑臂受到一半的叶片重力及叶片离心力；整个风轮由10个支撑臂共同承担，故单个支撑臂受到十分之一的叶片转矩.在额定转速下支撑臂的计算载荷：自身重力为56.8 N，自身离心力为1 000.7 N，叶片重力为23.3 N，叶片离心力为410.6 N，叶片转矩为3.2 N·m.

将支撑臂和叶片之间存在的叶片连接装置以及支撑臂和法兰盘的固定孔进行简化.并在网格划分前，对尺寸较小的面进行局部加密，对支撑臂自动生成网格，网格划分后得到支撑臂的有限元模型具有67 389个单元，106 775个节点.将支撑臂通过法兰盘与主轴固定的下端面施加x,y,z方向上的位移自由度全约束；将支撑臂通过叶片固定套筒与叶片固定的上端面固定孔通过圆柱面进行约束；支撑臂自重，施加重力加速度；支撑臂离心力，以主轴为旋转轴施加惯性载荷里的旋转速度；施加叶片重力载荷；施加叶片的离心力载荷；施加叶片作用于支撑臂的转矩载荷.额定转速下运行时支撑臂的位移变形和应力分布如图4所示.

由图4a分析可知，支撑臂的最大位移变形发生于支撑臂中间部分，最大位移变形量为0.25 mm，由中间部分向外位移变形量逐渐变小，直至支撑臂固定端变为最小；由图4b分析可知，支撑臂的最大应力发生于支撑臂上端与叶片固定套筒的圆孔处，最大应力为25.63 MPa，在其焊接部分又出现一处较大应力，其余部分受到应力较小，因此，需要在支撑臂焊接处进行加固，增加支撑臂的稳定性.

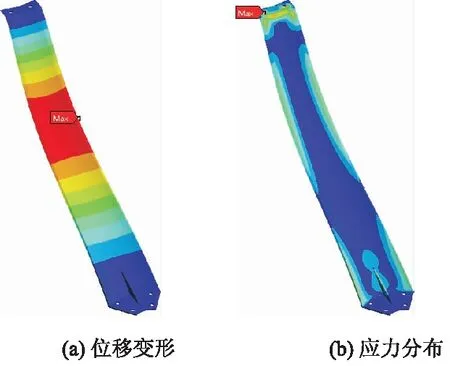
图4 支撑臂静力学分析云图

由式(16)计算可知，δmax=25.63 MPa<156.67 MPa，支撑臂结构设计合理，在额定转速下强度可以达到设计要求.

3.3 主 轴

主轴主要受到自身重力载荷、法兰盘转动而产生的转矩载荷以及风轮对主轴的压力载荷等.主轴计算载荷：自身重力为9.8 N，风轮重力为810.6 N，风轮转矩为31.8 N·m.

为了节省计算资源，简化主轴键槽、螺纹结构，对主轴自动生成网格，得到主轴有限元模型具有90 813个单元，135 760个节点.主轴底端和发电机连接，将主轴下端面施加x,y,z方向上的位移自由度全约束；主轴自重，施加重力加速度；施加风轮作用于主轴的压力载荷；施加风轮作用于主轴的转矩载荷.加载完成后开始进行求解计算，位移变形和应力分布如图5所示.

图5 主轴静力学分析云图

由图5a分析可知，主轴的最大位移变形发生于主轴顶端边缘部分，最大位移变形量为0.013 mm，由最大位移变量处向下逐渐变小，直至主轴的底端变为最小；由图5b分析可知，主轴的最大应力发生于主轴的底端，最大应力为11.70 MPa，从底端向上逐渐变小，直至主轴的顶端变为最小.由式(16)计算可知，δmax=11.70 MPa<266.67 MPa，主轴结构设计合理，在额定转速下强度可达到设计要求.

3.4 法兰盘

法兰盘主要受到自身重力载荷、风轮对法兰盘的压力载荷以及风轮转动而产生的转矩载荷.法兰盘计算载荷：自身重力为97.9 N，风轮重力为810.6 N，风轮转矩为31.8 N·m.

法兰盘网格类型采用带节点的四面体网格，采用自动划分的方式自动生成网格，得到法兰盘的有限元模型具有341 767个单元，511 182个节点.法兰盘固定孔固定于主轴之上，将法兰盘固定孔面施加x,y,z方向上的位移自由度全约束；法兰盘自重，施加重力加速度；施加风轮的压力载荷；施加风轮作用于法兰盘的转矩载荷.加载完成后开始进行求解计算，位移变形和应力分布如图6所示.

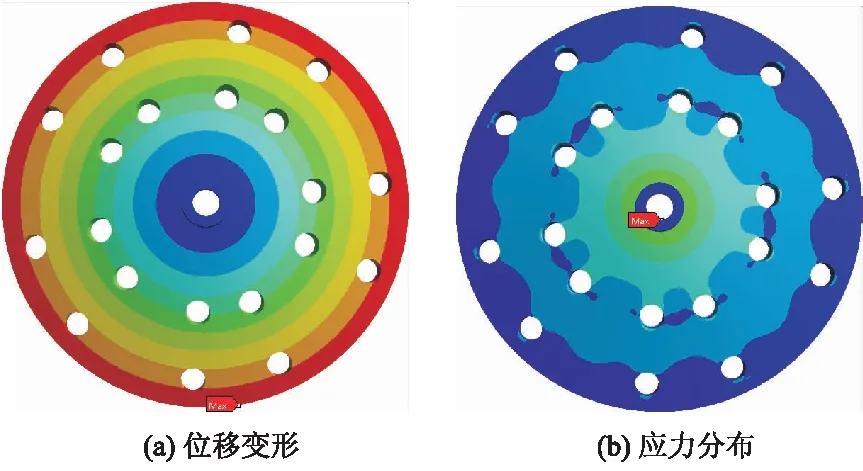
图6 法兰盘静力学分析云图

由图6a可知，法兰盘的最大位移变形发生于法兰盘外边缘，最大位移变形量为0.005 6 mm，并由外边缘向内逐渐变小，直至法兰盘中心部分降至最小；由图6b可知，法兰盘的最大应力发生于法兰盘突出柱与法兰盘平面的焊接处，最大应力为6.10 MPa，并由内向外，应力逐渐减小.因此，需在法兰盘焊接处进行加固，增加法兰盘的稳定性.

由式(16)计算可知，δmax=6.10 MPa<156.67 MPa，法兰盘结构设计合理，在额定转速下强度达到设计要求.

3.5 聚风罩

聚风罩起到聚风的作用，固定于风轮上下，主要受到自身的重力载荷以及风吹过聚风罩带来的气动载荷等.聚风罩计算载荷：上、下聚风罩的自身重力分别为318.2，311.3 N；气动载荷分别为53.0，53.0 Pa.

对聚风罩自动生成网格，得到上聚风罩的有限元模型具有的233 043个单元，468 728个节点；下聚风罩的有限元模型具有的476 650个单元，899 238个节点.对上聚风罩顶端面、下聚风罩底端面施加x,y,z方向上的位移自由度全约束；聚风罩自重，施加重力加速度；风吹过聚风罩引起气动载荷，以压力载荷的形式施加于上聚风罩的迎风面.加载完成后开始进行求解计算，位移变形和应力分布如图7所示.

由图7a分析可知，上聚风罩的最大位移变形发生于上聚风罩的底端中心处，其整个底端向外凸，最大位移变形量为0.63 mm，并由中心部分向外逐渐变小，侧面部分位移变形量整体较小；由图7b分析可知，上聚风罩的最大应力发生于底端的拐角处，最大应力为4.68 MPa，并由此处沿着侧面应力分布先变大后变小，在底端面由外边缘向中心先变小后变大；由图7c分析可知，下聚风罩的最大位移变形发生于顶端中心处，其整个顶端向内凹，最大位移变形量为1.20 mm，并由中心部分向外逐渐变小，侧面部分位移变形量较小；由图7d分析可知，下聚风罩的最大应力发生于下聚风罩下端的顶端中心处，最大应力为2.11 MPa，并由此处在顶端部分由内向外先减小后增大，在侧面部分应力分布逐渐变小.由式(16)计算可知，上聚风罩δmax=4.68 MPa，下聚风罩δmax=2.11 MPa，都在其所能承受的最大载荷之内，聚风罩结构设计合理，强度符合设计要求.

图7 聚风罩静力学分析云图

3.6 塔 筒

塔筒固定于地面之上起到支撑整个风力发电机的作用.塔筒主要受到自身的重力载荷、整个风力发电机的压力载荷和转矩载荷、风轮水平轴向推力载荷以及风吹过塔筒引起的气动载荷.塔筒计算载荷：自身重力为3 573.4 N，风力发电机重力为3 000.0 N，风轮转矩为31.8 N·m，水平轴向推力为72.5 N，气动载为53.0 Pa.

对塔筒自动生成网格，得到塔筒的有限元模型具有的347 864个单元，668 511个节点.塔筒底端固定于地面之上，在此面施加x,y,z方向上的位移自由度全约束；塔筒自重，施加重力加速度；风力发电机重力，施加压力载荷；水平轴向推力，施加压力载荷于塔筒的轴向；风吹过塔筒而引起气动载荷，以压力载荷的形式施加于塔筒的迎风面.求解计算得到位移变形和应力分布如图8所示.

图8 塔筒静力学分析云图

由图8a分析可知，塔筒的最大位移变形发生于塔筒顶端，最大位移变形为0.05 mm，并由顶端到塔筒根部逐渐减小.由图8b分析可知，塔筒最大应力2.28 MPa，从塔筒根部焊接处沿塔筒逐渐变小.

由式(16)计算可知，δmax=2.28 MPa<266.67 MPa，塔筒结构设计合理，强度达到设计要求.

4 风轮结构模态分析

进行叶片模态分析时，只需对风轮的主轴下端面施加位移自由度全约束即可，前六阶模态固有频率fi如表2所示，前六阶模态振型如图9所示.

表2 风轮前六阶模态固有频率

由图9分析可知，风轮的机身发生微小形变至忽略不计，前六阶模态下，最大变形发生于叶尖处，其变形数值也较小，基本不会发生较大的变形影响.

风轮工作频率为

(17)

(18)

式中：f为风轮1P频率，Hz；n为风轮额定转速，150 r/min.

计算得风轮工作频率f=2.5 Hz.根据工程经验，当满足式(18)时，风轮将不会发生共振现象.风轮固有频率与工作频率对比结果如表3所示,表中R为相对差.

图9 风轮前六阶模态振型

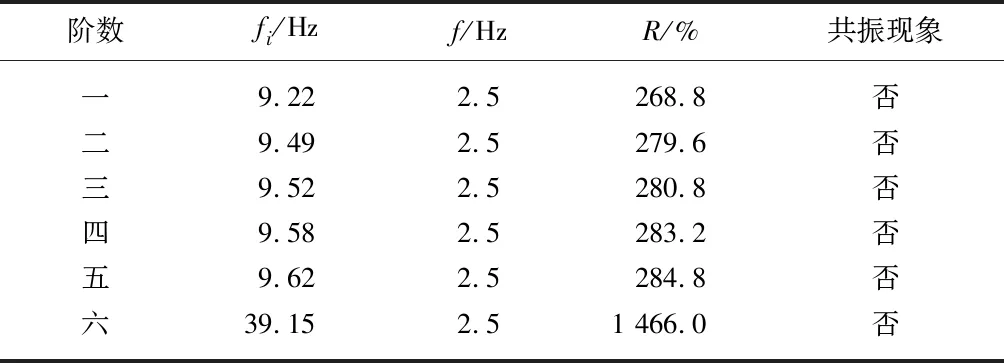
表3 风轮固有频率与工作频率对比

由表3分析可知，在额定转速下，风力机风轮的工作频率远远小于其固有频率，因此该风轮转动过程中在安全区之内，不会发生共振现象，安全可靠.

5 结 论

1) 基于ANSYS有限元分析软件，对所设计风力机的主要结构部件进行静力学分析，分析表明，叶片、主轴、支撑臂、法兰盘、上下聚风罩和塔筒等主要结构部件的最大位移形变均在材料所能承受的强度范围之内，影响可以忽略不计.

2) 对风力机的风轮进行了模态分析，求解得到其在转动工况下的前六阶固有频率和相对应的振型，通过分析振型以及对比固有频率可得，风轮的工作频率2.50 Hz远远小于其一阶固有频率9.22 Hz，可判定风轮在转动过程中不会发生共振，结构安全可靠.