水电站排沙漏斗水沙运动规律

洪振国，田辉

(云南省水利水电勘测设计研究院，云南 昆明 650021)

漏斗式排沙已经成为了经济、节水、高效泥沙处理的一种技术，并在灌溉、水电、引水工程等各领域成功应用，取得了较好的环境效益、经济效益、社会效益[1],受到国内外学者的广泛关注.1975年俄罗斯专家SALAKHOV[2]提出了的环流室理论，随后芬兰、伊朗、中国等多个国家的专家进行了排沙漏斗结构分析和优化研究[3].1984年四川大学高速水力学国家重点实验室和新疆农业大学水工实验室对排沙漏斗涡流的清、浑水流场进行了试验[4]，排沙漏斗首次在新疆迪那河总干渠工程应用.

目前，国内排沙漏斗的排沙效果、结构优化等方面取得了较好的成果.王顺久等[5]进行了排沙漏斗特性模型试验研究及其工程应用，刘善均等[6]进行了排沙漏斗优化及输沙特性试验研究.但是排沙漏斗中存在的吸气旋涡和泥沙湍流扩散导致泥沙运动规律十分复杂，目前排沙漏斗的水沙运动规律尚不清楚.文中以燕子崖水电站为例，通过数学模型计算分析排沙漏斗水沙运动规律，并采用物理模型试验论证数学模型计算合理性.

1 工程概况

燕子崖水电站为引水式径流电站，装机容量为30 MW，年利用时长为6 276 h，开发任务为单一发电.主要建筑物由大坝、引水渠道、排沙漏斗、无压引水隧洞、前池、压力钢管道、电站厂房等组成[7-8].大坝坝顶全长64.700 m，最大坝高为13.945 m，排沙漏斗直径为16 m，引水隧洞全长5 797.078 m，压力前池长70.004 m，顶宽10 m.压力钢管道上游接压力前池，管道长428.6 m；下游接水轮机.多年平均总输沙量为104万t，其中多年平均推移质输沙量、悬移质多年平均输沙量分别为17.3万t,86.7万t.

燕子崖水电站设计水头为204.12 m，水流通过水轮的相对流速为3.260 m/s；多年平均水中泥沙质量浓度为1.59 kg/m3，排沙漏斗排除的泥沙最小危害粒径为0.25 mm；泥沙颗粒级配见表1，表中d，ws，v分别为分组粒径、泥沙质量分数、粒径沉降速度.

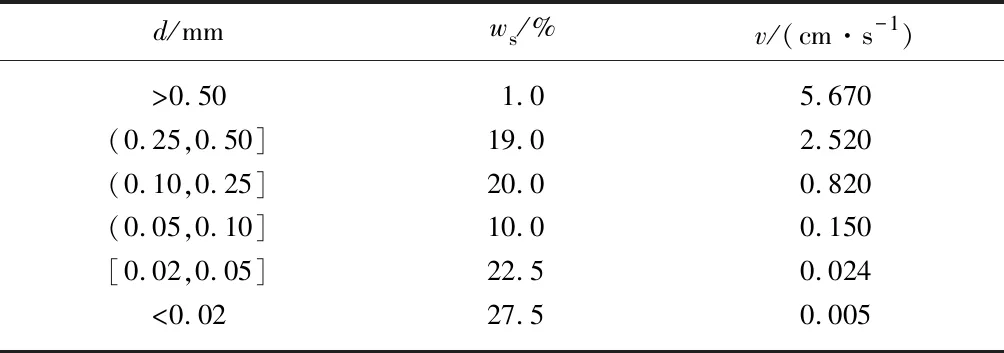
表1 泥沙颗粒级配

排沙漏斗结构主要由漏斗进水涵洞、悬板、漏斗、溢流堰、排沙底孔和排沙廊道等组成[9-10]，平面结构如图1所示.

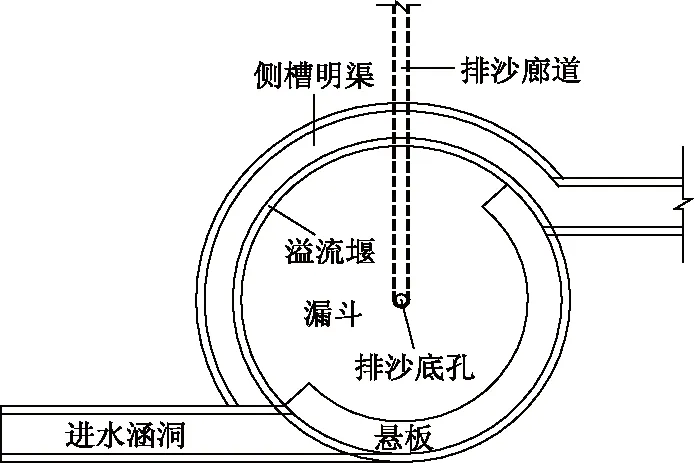
图1 排沙漏斗平面图

含沙水流通过进水涵洞进入漏斗，在悬板和漏斗边壁的约束作用下产生螺旋流；螺旋流进行水沙分离，泥沙从排沙底孔进入排沙廊道并排走，较清的水从溢流堰流入原引水渠道.排沙漏斗进水涵洞流量为16 m3/s，进水涵洞断面尺寸为1.8 m×1.8 m，底坡i=0.005，长20 m，底板高程为1 671.594 m.漏斗按圆形结构设计，漏斗直径为16 m，衬砌厚60 cm.溢流堰堰长20 m，堰顶高程为1 673.294 m.排沙底孔按圆形结构设计，直径为32 cm.排沙廊道按Φ400钢管长60 m设计，底坡为2.5%，排沙廊道的水直接排至漾弓江.侧槽明渠宽2.5 m，高度为3 m.

2 数学模型

2.1 控制方程

采用流体体积模型(VOF)方法耦合和雷诺应力模型(RSM)计算排沙漏斗清水流场，控制方程为

(1)

式中：ρ为流体密度；t为时间；Ui为时均速度；χi为水力参数.

泥沙颗粒的运动方程为

(2)

式中：mp为泥沙颗粒质量；up为泥沙颗粒速度；g为重力加速度；ρp为泥沙颗粒密度；FD为悬移质泥沙颗粒在水流中受到的阻力；Fp为水平方向压强梯度力；FV为虚拟质量力.

2.2 计算方法

数学模型计算采用有限体积法离散控制方程，采用SIMPLEC算法求解压力-速度的耦合.压力插值格式为Presto格式，采用二阶迎风格式对流项离散，对时间项采用二阶隐式格式离散.采用几何重建格式构建自由水面，采用五阶Runge-Kutta变步长积分法进行泥沙运动轨迹模拟，排沙漏斗含泥沙量根据泥沙颗粒的运动方程确定.

2.3 边界条件

进水涵洞入口为水流进口边界，根据断面面积和流量求解速度大小.溢流堰出口、漏斗顶部边界和排沙底孔出口等边界为大气压边界条件，采用壁面函数法得到壁面近邻控制体的流速与耗散率等.泥沙从进水涵洞入口断面进入计算区域，入口断面的泥沙分布均匀，速度等于水流进口速度.排沙漏斗进水涵洞高0.225 m,宽0.225 m；排沙漏斗直径为2 m、径向底坡为90%；排沙底孔直径为6.25 cm；其他参数、排沙漏斗数学模型结构图与模型试验的物理模型结构图一致.

2.4 网格划分

采用八结点六面体结构网格单元剖分计算区域，采用三角形非结构网格单元剖分漏斗与进水涵洞连接部位，共生成网格单元2.7×105个，在漏斗中心轴附近的网格单元较密集.

3 物理模型试验

排沙漏斗物理模型采用有机玻璃制作，模型试验流量由90°直角三角堰测量，流速测试采用声学多普勒流速仪(ADV)测量三维流速；含沙量采用自制的虹吸式采样器采集浑水，然后用烘干法测量.

排沙漏斗物理模型按照重力相似准则设计，由进水涵洞、漏斗、排沙底孔、悬板组成.物理模型比尺为1∶8，排沙漏斗直径和径向底坡、排沙底孔直径与数学模型的一致.排沙漏斗进口流量为15.6 L/s，泥沙质量浓度为1.59 kg/m3，排沙漏斗主要用于排除粒径大于0.25 mm的泥沙，物理模型沙使用粉煤灰筛分得到.

测试断面布置如图2所示，流速测试断面选择2个垂直断面，分别命名为断面A，B；每个测试断面布置5条间距为16 cm的水平测线，其中悬板与最上面的水平测线距离为6 cm，每条水平测线从距离漏斗室中心轴20 cm的径向位置开始往外每隔10 cm布设1个测点，最远的水平测点其径向位置半径为60 cm.

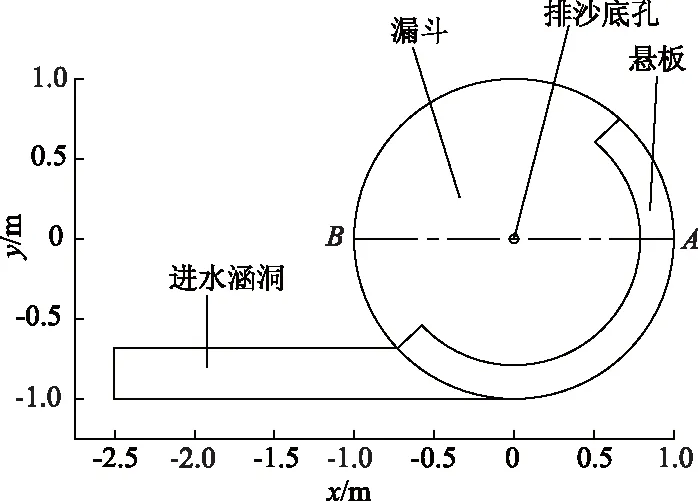
图2 测试断面布置示意图

4 结果分析

经过排沙漏斗数学模型计算和物理模型试验，得到断面A和B上的水流切向流速分布，如图3所示，图中r，vt分别为径向位置半径、切向速度.

图3 断面A和B上的水流切向速度分布

由图3得到断面A和B上的水流切向流速运动规律，见表2.由表中运动规律可知：切向流速总体呈现中间小、两头大的特点，在排沙底孔位置产生空气漏斗，空气漏斗周围产生强迫涡流.强迫涡流具有高排沙能力，在径向位置半径较大区域里，在漏斗圆形边壁的约束下，促使水体产生一个强迫涡.

表2 断面A和B上的水流切向流速运动规律

由图3得到断面A和B上的切向流速数学模型计算值和物理试验值，见表3，表中vtt，vtc分别为切向速度试验值与计算值.由表可知切向速度数学模型计算值与物理试验值相差较小，因此物理模型试验验证了由数学模型计算切向速度是可行的.

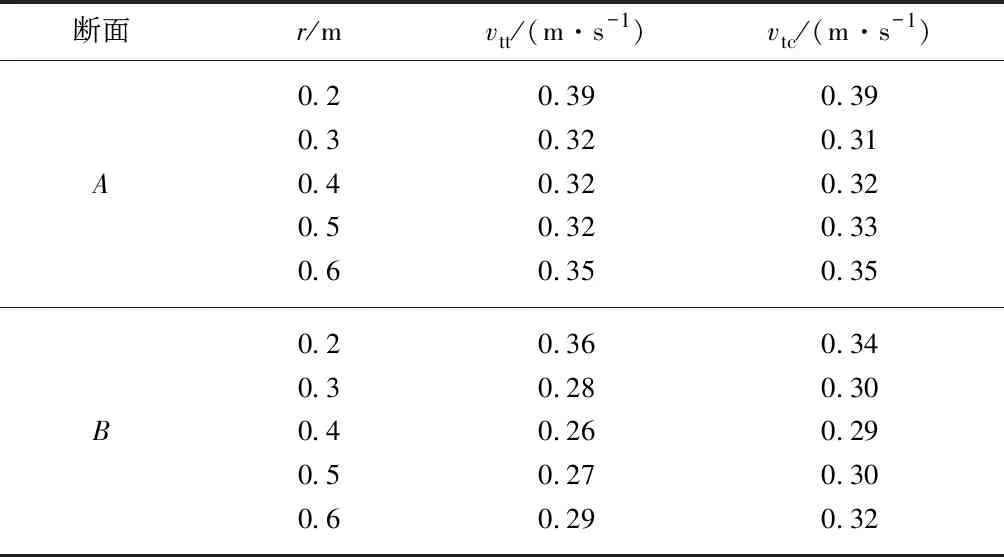
表3 断面A和B上的切向流速数学模型计算值和物理试验值

经过排沙漏斗数学模型计算和物理模型试验，得到断面A和B上的径向流速分布，如图4所示，图中vr为径向速度.图中正值表示径向流速指向漏斗中心轴，即向内；负值表示向外.

图4 断面A和B上的水流径向速度分布

由图4得到断面A和B上的水流径向流速运动规律，见表4.由表中运动规律可知：径向流速整体上随径向位置半径增大而先小后大，方向由内到外，在漏斗排沙底孔位置存在向内的、较大的径向流速，快速地把内侧区域底的泥沙运移至排沙底孔.

表4 断面A和B上的水流径向流速运动规律

由图4得到断面A和B上的径向流速数学模型计算值和物理试验值，见表5，表中vrt，vrc分别为径向速度试验值与计算值.由表可知径向速度数学模型计算值与物理试验值相差较小，因此物理模型试验验证了由数学模型计算径向速度是可行的.

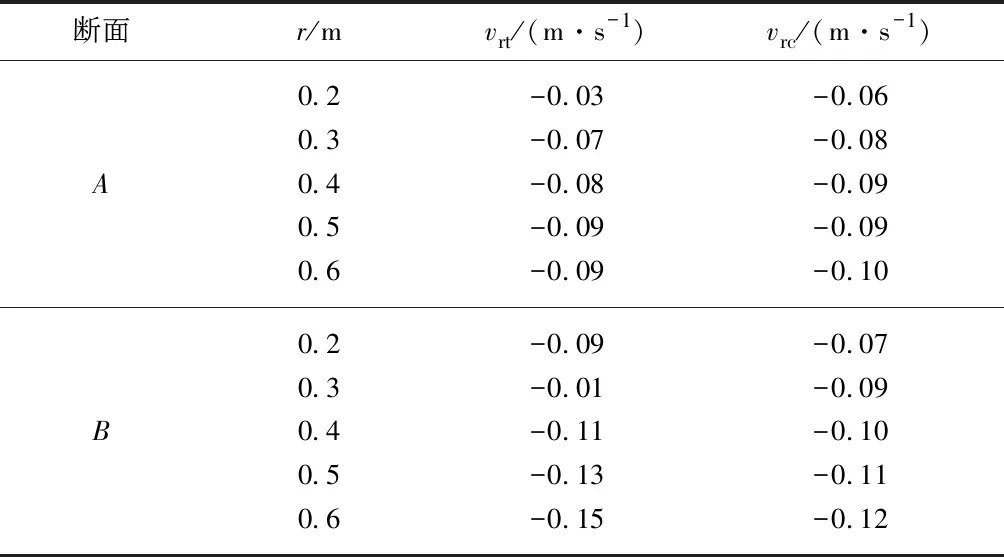
表5 断面A和B上的径向流速数学模型计算值和物理试验值

经过排沙漏斗数学模型计算和物理模型试验，得到断面A和B上的轴向流速va分布，如图5所示.图中正值表示向上，负值表示向下.

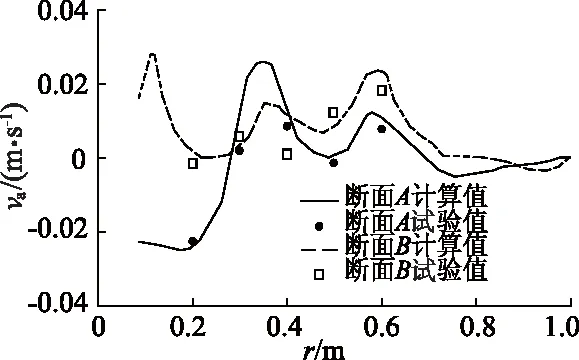
图5 断面A和B上的水流轴向速度分布

由图5得到断面A和B上的水流轴向流速运动规律，见表6.由表中运动规律可知，轴向速度值随径向位置半径增大作上下波动而波幅逐渐减小，轴向流速波动变化较为强烈并形成一个势涡，在漏斗圆形边壁的约束下促使水体产生一个强迫涡流.强迫涡流具有高排沙能力，将漏斗排沙底孔附近的泥沙快速运移至排沙底孔，通过与排沙底孔连接的排沙廊道排走泥沙.

表6 断面A和B上的水流轴向流速运动规律

由图5得到断面A和B上的轴向流速数学模型计算值和物理试验值，见表7.表中vat，vac分别为径向速度试验值与计算值.由表可知轴向速度数学模型计算值与物理试验值相差较小，因此物理模型试验验证了由数学模型计算轴向速度是可行的.

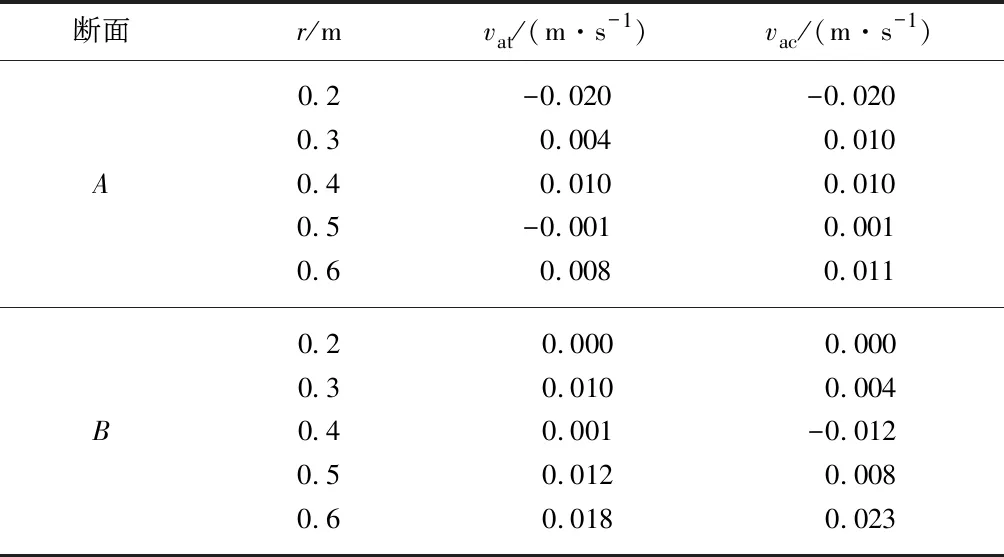
表7 断面A和B上的轴向流速数学模型计算值和物理试验值

经过排沙漏斗数学模型计算和物理模型试验，得到断面A和B上的垂向含沙量分布，如图6所示，图中h，ω分别为相对水深、泥沙质量浓度.

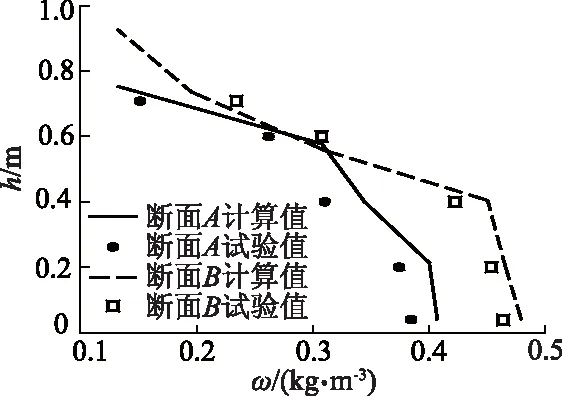
图6 断面A和B上的垂向含沙量分布

由图6得到断面A和B上的垂向含泥沙量分布规律，见表8.由表8的分布规律可知，漏斗内含泥沙量整体垂向分布为“上小下大”型分布，含泥沙量在近底部附近较高，底部附近形成较高含泥沙水流，悬板使漏斗在排沙底孔轴线上充分发展，使排沙底孔过水断面减小，排沙漏斗具有截沙率高、耗水率低的优点.

表8 断面A和B上的垂向含泥沙量分布规律

由图7得到断面A和B上的垂直向含沙量数学模型计算值和物理试验值，见表9，表中ωt，ωc分别为泥沙质量浓度试验值与计算值.

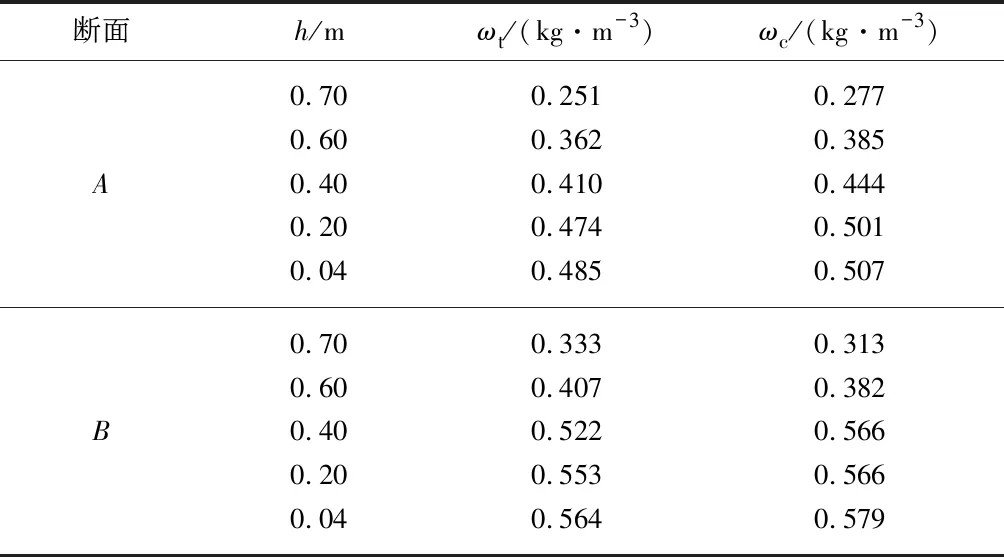
表9 断面A和B上的垂向含沙量数学模型计算值和物理试验值

由表9可知，垂向含泥沙量数学模型计算值与物理试验值相差较小，因此物理模型试验验证了由数学模型计算垂向含泥沙量是可行的.

5 结 论

1) 排沙漏斗切向流速总体呈现中间小、两头大的特点；径向流速随径向位置半径增大而先小后大，方向由内到外；轴向速度值随径向位置半径增大作上下波动而波幅逐渐减小.在漏斗圆形边壁的约束下，水体产生一个强迫涡流；强迫涡流具有高排沙能力，将漏斗排沙底孔附近的泥沙快速运移至排沙底孔，通过与排沙底孔连接的排沙廊道排走泥沙.

2) 排沙漏斗内含泥沙量整体垂向分布为“上小下大”型，含泥沙量在近底部附近较高，形成含泥沙量较高的水流.悬板使漏斗在排沙底孔轴线上充分发展，使排沙底孔过水断面减小.排沙漏斗具有截沙率高、耗水率低的优点.

3) 排沙漏斗切向、轴向、径向流速，以及含泥沙量数学模型计算值与物理试验值相差较小，因此物理模型试验验证了由数学模型计算是可行的.