对数螺旋锥齿轮啮合仿真分析*
□ 肖 扬 □ 陈董燕 □ 侯圣宇
1.西南石油大学 机电工程学院 成都 6105002.中国航发航空科技股份有限公司 成都 610503
1 分析背景
螺旋锥齿轮是实现相交轴传递运动和动力的一种基本部件,在机器中得到大量应用。螺旋锥齿轮的质量和精度对机器工作的质量、精度会产生非常大的影响。对数螺旋锥齿轮由于齿廓形成时的几何特性,可以使啮合时的轮齿重叠因数增大。对数螺旋锥齿轮比一般锥齿轮传动比大,能够得到啮合较好的齿轮副,承载能力更强,运转更加平稳,齿轮寿命也是一般锥齿轮的4~10倍,高速运转时的振动及噪声显著减小,目前已广泛应用于航天、航空、汽车等各种精密、高速、重载传动领域。对数螺旋锥齿轮的工作情况、制造精度、质量直接影响机器的质量、效率、噪声、运动精度、寿命等,因此,对数螺旋锥齿轮精确模型啮合时的运动情况、工作情况、接触斑点、传动误差,以及负载时齿面上弯曲应力和接触应力分布等问题,一直引起各国学者的研究和关注,成为齿轮设计生产中非常重要的技术问题。对以上问题进行分析和解决,可以大幅提高螺旋锥齿轮的设计和制造水平,满足科技发展中对高质量机器的需求。
对数螺旋锥齿轮的轮齿由左右两个齿廓曲面,锥顶、锥底两个圆锥面,以及前锥、背锥面围成。左右两个齿廓曲面以空间球面渐开线为齿廓曲线,以圆锥对数螺旋线为发生线运动而形成。建立对数螺旋锥齿轮三维模型时,通过点云逆向近似,或者基于简化的对数螺旋锥齿轮有限元模型,分析模型与实际对数螺旋锥齿轮的形状有偏差,分析结果不可避免地会产生不准确。笔者在对数螺旋锥齿轮精确三维模型的基础上进行仿真分析[3],应用ANSYS Workbench 软件对齿轮啮合分别进行静态和动态接触分析,获得较为准确的接触工作情况变化规律。对数螺旋锥齿轮精确三维模型如图1所示。

▲图1 对数螺旋锥齿轮精确三维模型
2 静态接触分析
2.1 参数
在齿轮工作过程中,只会有很少几对轮齿进行啮合,没有啮合的轮齿不存在接触应力。因此,在静态接触分析时,忽略大齿轮的非啮合轮齿对综合刚度矩阵的影响,将啮合模型简化为六齿模型来进行啮合分析。对数螺旋锥齿轮参数见表1。
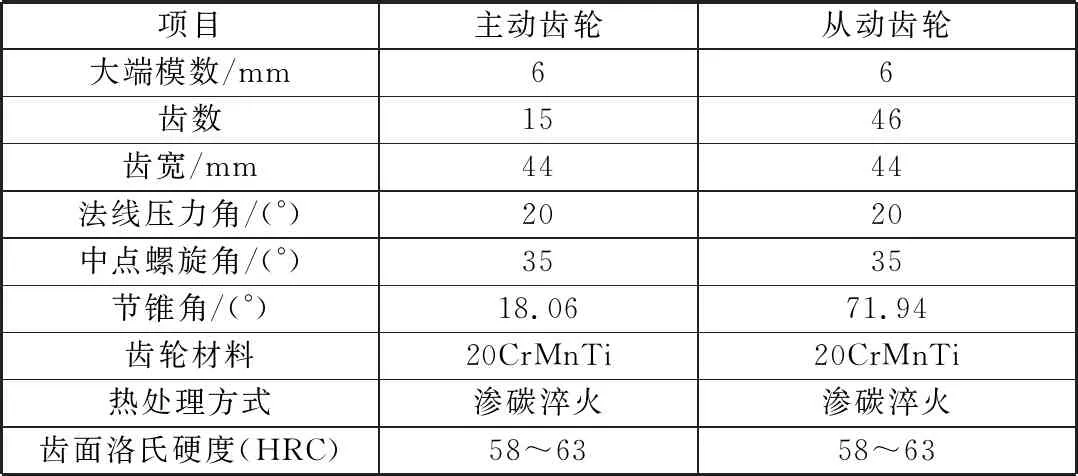
表1 对数螺旋锥齿轮参数
2.2 有限元建模
根据表1,两个啮合的对数螺旋锥齿轮的材料为20CrMnTi,密度为7.85×103kg/m3,弹性模量为206 GPa,泊松比为0.3。
ANSYS Mesh软件拥有几种不同的网格划分方法,网格的疏密程度会直接影响求解结果的精确性,且过密的网格会使计算成本增加。为了获得更精确的计算结果,同时考虑对数螺旋锥齿轮的复杂结构特点及边界条件与载荷,采用混合四面体和六面体网格划分,并且对参与啮合的对数螺旋锥齿轮接触齿面进行局部细化。为减小计算量,只取从动齿轮的六齿模型进行求解,并且保证计算的精度。对数螺旋锥齿轮啮合接触部位网格细化如图2所示。
应用ANSYS Workbench软件对对数螺旋锥齿轮进行啮合接触分析时,需要定义齿轮的接触区域。因对数螺旋锥齿轮啮合齿面的复杂性,笔者采取面面接触中的自动接触方式来定义接触对,并对有定义接触关系的接触面进行判断和求解,将主动齿轮定义为接触面,将从动齿轮定义为目标面,所定义的接触对如图3所示。在ANSYS Workbench软件中采用罚函数来对非线性接触进行计算。

▲图2 对数螺旋锥齿轮啮合接触部位网格细化
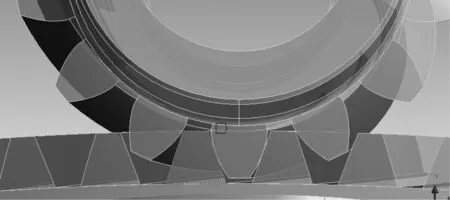
▲图3 对数螺旋锥齿轮接触对定义
所有接触问题都必须定义接触刚度,包括法向刚度和切向刚度。法向刚度是最大穿透容差和影响病态条件的关键因子,考虑到计算收敛等问题,取法向刚度因子为1。
穿透超过最大穿透容差,需要进行新的迭代计算。穿透容差取决于接触刚度,值太小则会使计算收敛困难。选取最大穿透容差为0.1。
考虑摩擦力因素的影响,在罚函数常温下选取对数螺旋锥齿轮接触面间的摩擦因数为0.06。
2.3 边界条件与载荷
对大对数螺旋锥齿轮内圈表面所有节点进行全约束,对小对数螺旋锥齿轮内圈控制节点的径向和轴向自由度进行固定,使绕轴旋转的周向自由度处于自由状态。对数螺旋锥齿轮由功率为500 kW的电动机驱动,对于高速传动对数螺旋锥齿轮,小齿轮主轴转速为10 000 r/min,计算得到驱动扭矩为300 N·m。求解中大变形开关开启,防止计算收敛困难。
2.4 求解
为了得到对数螺旋锥齿轮在啮合过程中齿面接触应力的分布情况,对静态状态下对数螺旋锥齿轮不同转角的啮合模型分别进行分析。在对数螺旋锥齿轮啮合过程中,转角范围为0°~2.16°,每0.72°取一个对数螺旋锥齿轮的啮合模型。通过分析,对数螺旋锥齿轮啮合模型在转角为0°、0.72°、1.44°、2.16°时的齿面接触应力云图如图4所示。

▲图4 对数螺旋锥齿轮齿面接触应力云图
取若干位置分别进行有限元接触分析计算的方法体现出两个特点。
第一,每个啮合位置的分析模型均可由主动齿轮的节点旋转约束实现,所以这一方法能够实现对数螺旋锥齿轮啮合周期内任一瞬时位置处的接触分析。
第二,不需要事先预设接触载荷的分布状况,因为在啮合接触状态下,ANSYS Workbench软件能够自动捕捉及计算接触区域与接触载荷分布情况。
从图4中可以看出,对数螺旋锥齿轮开始逐渐进入啮合,接触区域逐渐增大,齿面上的接触应力也逐渐增大。轮齿在啮合状态下,接触应力区域逐渐增大,接触应力也逐渐增大。观察接触斑点区域能够发现,各接触斑点区域在分布上呈现出直线型。在对数螺旋锥齿轮啮合的各个阶段,齿顶附近出现边缘接触现象,这会给高速重载工况下的对数螺旋锥齿轮传动带来不利影响。
齿轮啮合传动周期内的静力学接触分析结果说明,对数螺旋锥齿轮在接触斑点区域的轨迹在方向上大致呈直线型。在对数螺旋锥齿轮啮合过程中,从点接触扩展到面域接触,并且是从小端到大端同时向齿顶方向呈倾斜直线分布。
在啮合过程中,对数螺旋锥齿轮几乎始终有三对轮齿处于接触状态,因此对数螺旋锥齿轮承载能力强,传动平稳,传动效率高。在啮入过程中,接触斑点区域逐渐增大,最大接触应力也随之增大。对数螺旋锥齿轮齿面会发生边缘接触,对齿轮传动的稳定性产生影响。在对数螺旋锥齿轮啮出过程中,接触斑点区域逐渐减小,最大接触应力也逐渐减小。综合而言,对数螺旋锥齿轮在一个啮合周期过程中,轮齿齿面上的接触应力先增大后减小。
通过处理器求解,可以直观观察到装配体的应力、应变、位移,以及接触状态、接触应力等。初始位置处对数螺旋锥齿轮等效接触应力云图如图5所示,可以看出,最大等效接触应力为871.1 MPa。

▲图5 初始位置对数螺旋锥齿轮接触应力云图
从动齿轮、主动齿轮的等效应力云图分别如图6、图7所示。从图6和图7中可以看出从动齿轮、主动齿轮最大等效应力的位置。从动齿轮、主动齿轮的最大等效应力分别为274.7 MPa、366.3 MPa,最大等效应力位于接触线边缘靠近齿根处,轮齿边缘处有应力集中现象。相互啮合传动的主动齿轮等效应力比从动齿轮大,这是由于静态接触分析中,从动齿轮为全约束,力矩加载在主动齿轮上,在接触初始状态瞬间,主动齿轮接触冲击大于从动齿轮。

▲图6 从动齿轮等效应力云图

▲图7 主动齿轮等效应力云图
3 动态接触分析
在对数螺旋锥齿轮传动过程中,负载是逐齿传递的。在传递过程中,总会出现单齿、双齿交替啮合,引起齿轮啮合力振动与冲击,以及载荷与转速的波动,导致啮合刚度周期性变化。与此同时,存在啮合齿面间摩擦力等非线性因素,在不同啮合位置处经过多次静态接触来计算接触应力,也只考虑啮合过程中某一瞬态的情况,不能准确全面反映对数螺旋锥齿轮在传动过程中的力学特性。由于对数螺旋锥齿轮的工作环境往往为高速重载场合,为了真实模拟对数螺旋锥齿轮连续传动过程中整个周期的接触应力、应变等随时间的变化趋势,有必要对对数螺旋锥齿轮进行动态接触分析。
考虑转速等影响因素,笔者在ANSYS Workbench软件中建立对数螺旋锥齿轮接触分析有限元模型,对其进行瞬态动力学分析,得到传动过程中动态接触应力实时变化规律,同时分析高、中、低三种不同状态下动态啮合接触的应力变化规律,为对数螺旋锥齿轮的设计提供参考依据。
在对数螺旋锥齿轮动态啮合过程中,电动机通过联轴器为主动齿轮施加一个绕轴旋转的角速度,同时通过主动齿轮、从动齿轮的接触驱动使从动齿轮绕中心轴旋转,从动齿轮在输入转矩与负载阻力矩的作用下达到受力平衡。对主动齿轮施加绕中心轴旋转的角速度为1 000 rad/s,从动齿轮的阻力矩为120 N·m。
在瞬态分析设置中,打开大变形开关,载荷步结束时间设置为0.001 3 s,关闭自动时间步长开关,设置载荷步子步为30,采用稀疏矩阵求解器对非线性接触进行瞬态求解。计算求解过程中力收敛曲线如图8所示。计算残差值小于收敛容差值,表示收敛。计算收敛后,将出现虚线间断线,反之则出现点划线间断线。从曲线绕定值周期性振荡可以看出,非线性接触分析求解是收敛的。为了分析在啮合过程中不同时刻的接触情况,选取高速状态下0.000 213 s、0.000 214 s、0.000 581 s、0.000 625 s、0.000 801 s、0.000 90 s六个时刻的对数螺旋锥齿轮装配体接触状态,其等效应力云图如图9所示。
选取图9不同时刻各位置处的最大接触应力,得到不同啮合位置最大接触应力,见表2。
分析图9及表2可知,当对数螺旋锥齿轮处于高速状态下,齿轮啮入及啮出的最大接触应力大于单齿啮合时的最大接触应力,这是由于啮入及啮出点偏离理论啮入、啮出位置点,造成啮入、啮出冲击。双齿啮合最大接触应力明显远小于单齿啮合最大接触应力,这是由于载荷由多个轮齿分担,并且接触区域面积增大,综合啮合刚度变大,啮合接触弹性变形减小,使接触应力减小。
为了分析不同工况、不同转速对对数螺旋锥齿轮动态接触应力的影响,选取高、中、低三个有代表性的转速,在ANSYS Workbench软件中对啮合齿轮进行瞬态动力学分析求解,载荷边界条件见表3。

▲图8 力收敛曲线
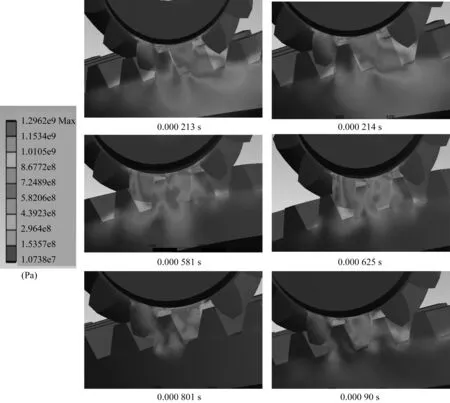
▲图9 高速状态下不同时刻等效应力云图

表2 高速状态下不同啮合位置最大接触应力

表3 载荷边界条件
在中速状态下,依据与转速相对应的啮合周期,设定载荷步结束时间为0.01 s,关闭自动时间步长开关,设置载荷步子步为40,提取0.004 52 s、0.005 77 s、0.005 82 s、0.006 77 s、0.008 25 s、0.009 6 s六个时刻对数螺旋锥齿轮各啮合位置的等效应力云图,如图10所示。
选取图10不同时刻各啮合位置处的最大接触应力,得到不同啮合位置最大接触应力,见表4。
分析图10及表4可知,对数螺旋锥齿轮啮入及啮出的最大接触应力稍大于双齿啮合时的最大接触应力,且与单齿啮合时接近,说明随着转速的降低,对数螺旋锥齿轮缓慢进入传动平稳期,受载变形也变化不大,齿轮受啮合冲击的影响减小。
在低速状态下,设定载荷步结束时间为0.08 s,关闭自动时间步长开关,设置载荷步子步为40,提取0.038 s、0.045 s、0.052 s、0.06 s、0.072 s、0.08 s六个时刻对数螺旋锥齿轮各啮合位置的等效应力云图,如图11所示。
选取图11不同时刻各啮合位置处的最大接触应力,得到不同啮合位置最大接触应力,见表5。
分析图11及表5可知,在低速状态下,对数螺旋锥齿轮啮入及啮出的最大接触应力与双齿啮合时的最大接触应力相差不大,且单齿啮合时最大接触应力相差越来越小,说明齿轮啮合在低转速情况下运动平稳,传动性能好。

▲图10 中速状态下不同时刻等效应力云图

表4 中速状态下不同啮合位置最大接触应力
上述三种转速状态下的对数螺旋锥齿轮啮合接触分析可知,在低速状态下,齿轮受载变形及冲击均较小,随着转速的提高,受载变形及冲击均增大。在恒定转矩下,转速是接触力幅值变化的主要因素之一。
4 结束语
在恒定转矩下,从对数螺旋锥齿轮静态与动态接触的等效应力云图可以观察到,静态与动态接触的接触线均是沿对数螺旋锥齿轮小端到大端并向齿顶方向倾斜的一条直线,且最大等效应力均处在接触线边缘靠近轮齿齿根处。在相同转矩情况下,动态接触应力比静态接触应力大,这是由于在啮合过程中齿轮受载变形,以及在内部激励作用下产生较大的啮合冲击,啮入、啮出点偏离理论位置点,使啮合齿轮产生线外啮合,从而引起周期性振动与冲击。相比静态接触分析,动态接触分析可以在一次算法中求解出啮合全过程所有时刻的啮合位置处接触应力变化规律,并且更接近实际工况。
笔者以对数螺旋锥齿轮的精确三维模型为基础,应用ANSYS Workbench软件对对数螺旋锥齿轮啮合传动过程中的工作情况进行静态、动态分析。
通过不同位置处的非线性静态接触分析,得到接触区域应力变化规律,并且在ANSYS Workbench软件中求解得到最大接触应力,结果与理论计算值比较,验证了有限元模型法计算接触问题的准确性。
另一方面,分析了不同转速状态下齿轮在不同啮合时刻的动态接触情况,比较转速对接触特性的影响规律。通过分析得到了对数螺旋锥齿轮工作时静态、动态性能的变化规律,为进一步研究、设计、制造对数螺旋锥齿轮打下了基础。

▲图11 低速状态下不同时刻等效应力云图

表5 低速状态下不同啮合位置最大接触应力

