联系测量方法在地铁施工中的应用

傅贵旺

中铁十七局铺架分公司，中国·山西 忻州 034300

1 引言

目前大、中城市正在极力发展地铁交通，地铁的发展主要依赖与地下工程隧道开挖等的相关技术的进步，测量施工作为地铁施工的重要组成部分，有着极为重要的作用。地下施工需要将地面的控制系统投影到地下，建立起统一的控制系统，而联系测量很好地解决了这个难题。

2 联系测量简介及要求

1.1 联系测量简介

联系测量是将地面的平面坐标系统和高程系统通过施工竖井传递到地下，使地上、地下坐标系统相一致的测量工作。其包括平面和高程传递，平面传递包括陀螺全站仪和铅垂仪组合定向、一井定向（联系三角法）、两井定向、导线直接传递测量、投点定向法等，也是常用于城市轨道交通工程中的定向测量方法。高程传递主要包括悬挂钢尺法、光电测距三角形法及水准测量法。

2.2 联系测量要求

联系测量是地下隧道施工和铺轨测量的重要环节，为了满足施工要求，确保测量精度，《城市轨道交通工程测量规范》制定出联系测量技术要求，我们必须在工作中严格遵守。

每次联系测量应独立进行三次，取三次平均值作为定向成果。地下近井定向边方位角中误差不应超过±8，地下近井工程高程中误差不应超过±5mm。

定向测量的地形近井定向边应大于120m，且不应少于2条，传递高程的地下近井高程点不应少于2 个。使用近井定向边和地下近井高程点前，应对地下近井定向边之间和高程点之间的几何关系进行检核，其不符值应分别小于12"和2mm。

3 平面传递测量

平面传递的测量方法很多，论文主要介绍一井定向和两井定向方法。

3.1 一井定向测量方法简介

一井定向测量也称联系三角形定向测量。一井定向是在一个竖井中悬挂两根钢丝，在地面近井点与钢丝组成三角形，并测定近井点与钢丝的距离和角度，从而算得两钢丝的坐标以及它们之间的方位角。在井下，同样井下近井点也与钢丝构成三角形，并测定井下近井点与钢丝的距离和角度。由于钢丝处于自由悬挂状态，可以认为钢丝的坐标和方位角与地面一致，通过计算便可获得地下导线起算点的坐标和方位角，这样就把地上与地下导线联系起来了。一井定向示意图见图1。在生产实践中，测量工作者总结出了双联系三角形定向测量方法，该方法是在竖井中悬吊三根钢丝，组成两个联系三角形[1]。这样能提高精度，且具有复核作用，操作也容易，在实际生产中得到广泛应用。

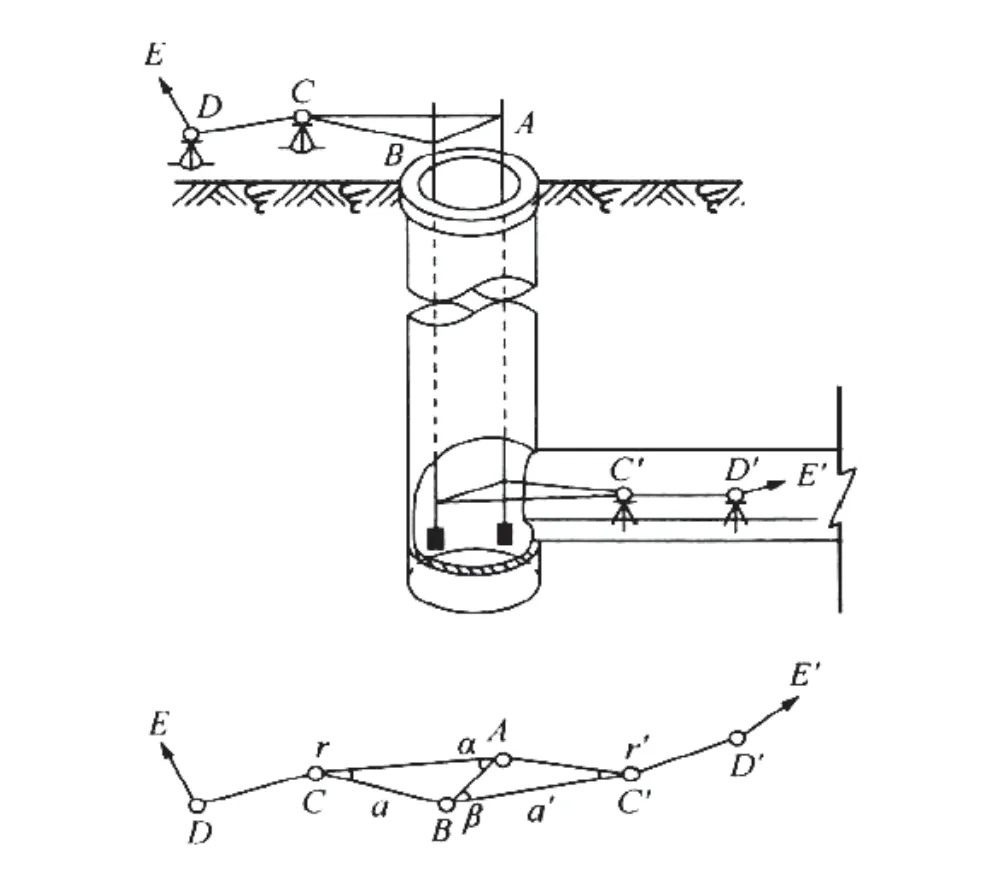
图1 一井定向示意图

联系三角形定向测量的关键技术要求如下：

（1）联系三角形中两根钢丝的间距C 应尽量长，角∝、γ 及β、γ 均宜小于1°，呈直伸三角形；及宜小于1.5，α'、α 为近井点至悬挂钢丝最短的距离。

（2）几何关系和数学模型。由于已精确测定地面及地下联系三角形ω、γ 及ω'、γ'，则地下控制边C'D'的坐标方位角为：

αC'D'=αCD+ω+α+γ+β+γ'+ω'±n*180°

式中，αCD为地面近井导线边方位角；ω、ω'分别为地上α 和β 地下连接角。

可通过联系三角形求得，根据三角函数有：

可根据导线坐标推算原理直接求得A、B 两点的坐标，进而求得C、D 两点的坐标。

由于每个联系三角形均观测三条边和一个内角，因此有一个多余观测值，可按边角网平差方法进行条件平差，这样可得各观测值的最佳估算值。地上地下平差模型均为：

c2= α2+ b2- 2ab cos γ

3.2 一井定向的实例应用

石家庄地铁3 号线东段东王站由于受现场条件限制，只有一个出土口可供联系测量使用。因此，我们在该站选用一井定向联系测量方法，测量示意图如下所示。

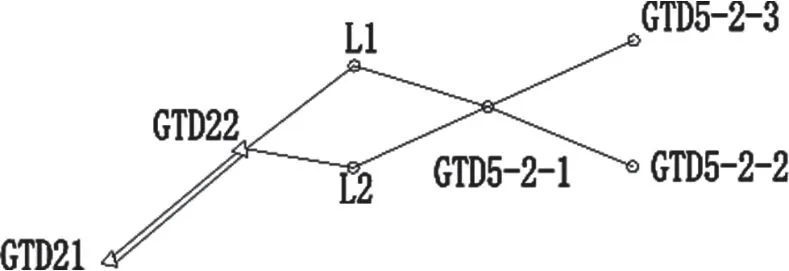
图2 东王站一井定向测量路线图

GTD21、GTD22 为起算，L1、L2 为钢丝，GTD5-2-1、GTD5-2-2、GTD5-2-3 为地下导线点。地面上从两个已知点起算，在近井点设站观测钢丝，同时在地下布置三个点，在GTD5-2-1 设站观测钢丝，地下三个点可构成两个基线边。本次解算采用科傻平差软件具体实测值及解算结果如图3、图4所示。

图3 平差所需实测值

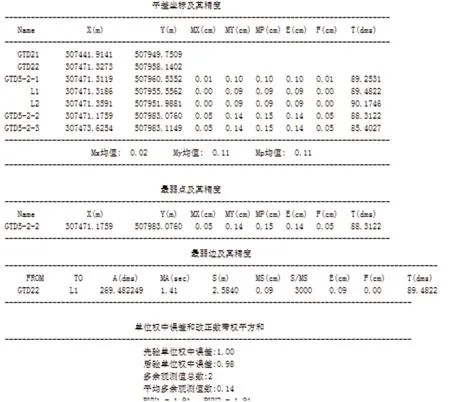
图4 平差结果及精度指标

3.3 两井定向测量方法简介

两井定向也是定向测量的一种常用方法，它适用于竖井井口小，两端均有井口（或可钻孔）的区域。两井定向是在两施工竖井（或钻孔）中分别悬挂一根钢丝。一方面，与一井定向相比，由于两钢丝间的距离大大增加，因此减少了投点误差引起的方向误差，有利于提高地下导线的精度，这是两井定向的主要优点。另一方面，外业测量比较简单，占用竖井的时间较短。两井定向时，利用地面上布设的近井点或地面控制点采用导线测量或其他测量方法测定两根钢丝的平面坐标值。在地下隧道中，将已布设的地下导线与竖井中的钢丝联测，即可将地面坐标系中的坐标与方向传递到地下去，经计算求得地下导线各点的坐标与导线边的方位角。

这时候地下导线与竖井钢丝的联测就构成了一个附和图形，但是在这个图形中，两根钢丝处分别缺少一个连接角，这样的导线是无起始方向角的，故称为无定向导线。其中，两井定向示意图如下所示。

图5 两井定向示意图

两井定向需注意近井点与钢丝的布置形状，尽量成一条线即呈现直伸型。地下两个待定点与钢丝也要尽量呈直伸型，且两点间距尽量要大，但是不能超出两条钢丝。

3.4 两井定向的解算

根据地面连接测量的成果,计算两垂球连线的方位角及长度。按一般计算方法，算出两垂球线的坐标xA,yA,xB,yB，根据算出的坐标，计算AB 的方位角及长度c:

按GB/T 50308-2017《城市轨道交通工程测量规范》规定，两井定向必须独立进行两次，两次求得的起始边方位角互差不得超过1'，取两次独立定向计算结果的平均值作为两井定向井下连接导线的最终值。

3.5 两井定向的实例应用

石家庄3 号线东段三教堂站完全具备客观条件，两个盾构井跨越东二环，空间距离完全满足实际条件，因此我们在该区间的联系测量中选用两井定向联系测量的方法，示意图如图6所示。

图6 三教堂两井定向测量络线图

其中XXIJ015、XXIJ019、TDHY、XXIJ020 为已知控制点，L1、L2 为两钢丝，1001、1002 为地下点。

应用平差软件解算过程如下：

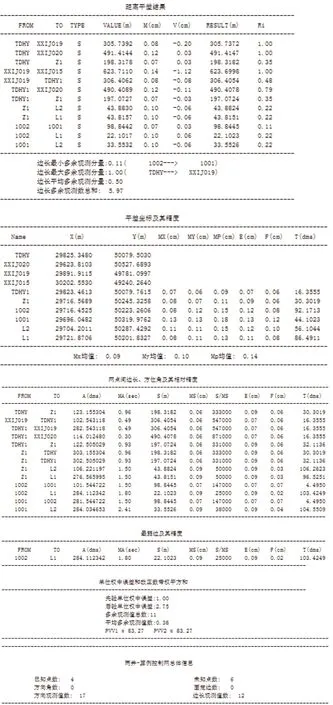
图7 平差所需观测值及平差结果和精度指标

4 高程传递测量

4.1 竖井高程传递

高程传递测量就是将地面坐标系统中的高程传递到地下、基坑中的高程点的测量工作。高程传递测量包括地面近井水准测量、高程传递测量以及地下近井水准测量。近井点应符合在一、二等水准点上，按照二等水准测量的技术要求。

高程传递的方法有：钢尺悬挂法、电磁波测距三角高程法、水准测量法。我们这里介绍钢尺悬挂法[2]。

钢尺悬挂法测量时，应在竖井内悬挂长钢尺与水准仪配合测量，如图8所示。

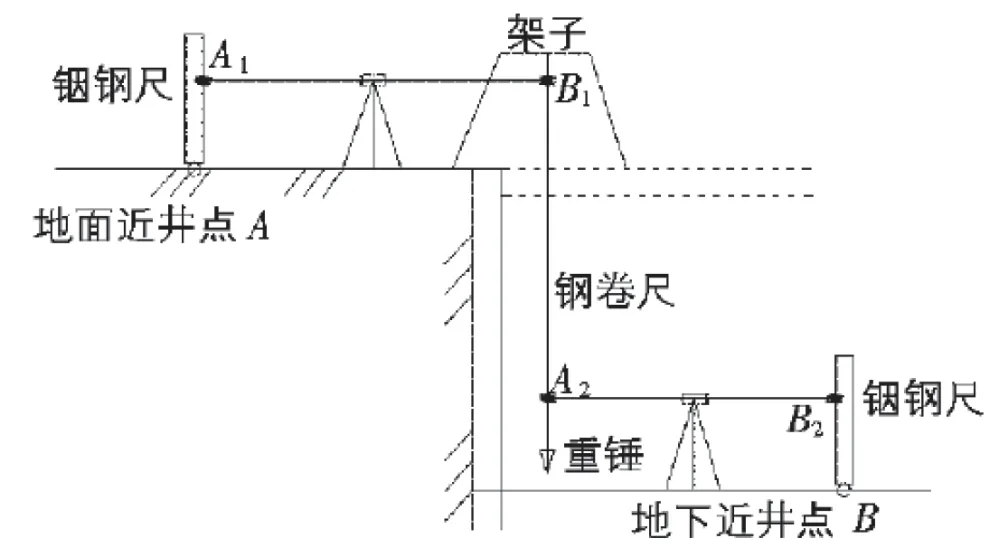
图8 钢尺悬挂法示意图

首先将经检定的长钢尺悬挂在竖井内，钢尺零点朝下，下端挂一重锤，并置于油桶中，使之稳定。在井上、井下各安置一台水准仪，精平后同时读取钢尺上的读数b1、α2，然后再读取地上、地下水准尺的读数α1、b2。测量时用温度计计量地上与地下的温度。由此可求取井下水准点B的高程HB为：

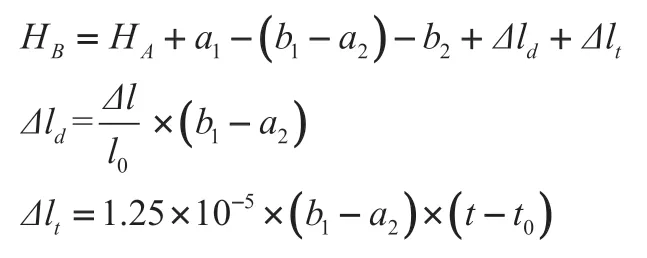
式中，HA为地面近井水准点或洞口为水准点的已知高程；Δld为尺长改正数；Δl为钢尺经检定后的一整尺的尺长改正数；l0为钢尺名义长度；Δlt为温度改正数；t为井上、井下温度平均值；t0为检定时温度（一般为20℃）。

4.2 钢尺悬挂法的注意事项如下：

（1）测定近井水准点高程应使近井水准点附和水准控制点上，并按规范满足水准测量的有关技术要求。

（2）观测钢尺读数时应使地上和地下两台水准仪同时读数，钢尺悬挂的重锤应尽量等同于检定时的重量，高差应进行温度。尺长改正，当井深超过50m 应进行钢尺自重张力改正。

（3）传递高程时，每次应独立观测三测回，测回间应变动仪器高，三测回测得地上、地下水准点间的高差较差应小于3mm。

4.3 高程传递的实际应用

石家庄地铁东段大部分车站都具备钢尺悬挂法，而且施测条件相对容易满足。论文选取塔冢站作为例子，首先车站深度适中，50m 钢尺完全满足长度要求，而且铺轨基地设在本站，悬挂钢尺方便快捷。现场实测值及内业数据解算过程如表1所示。

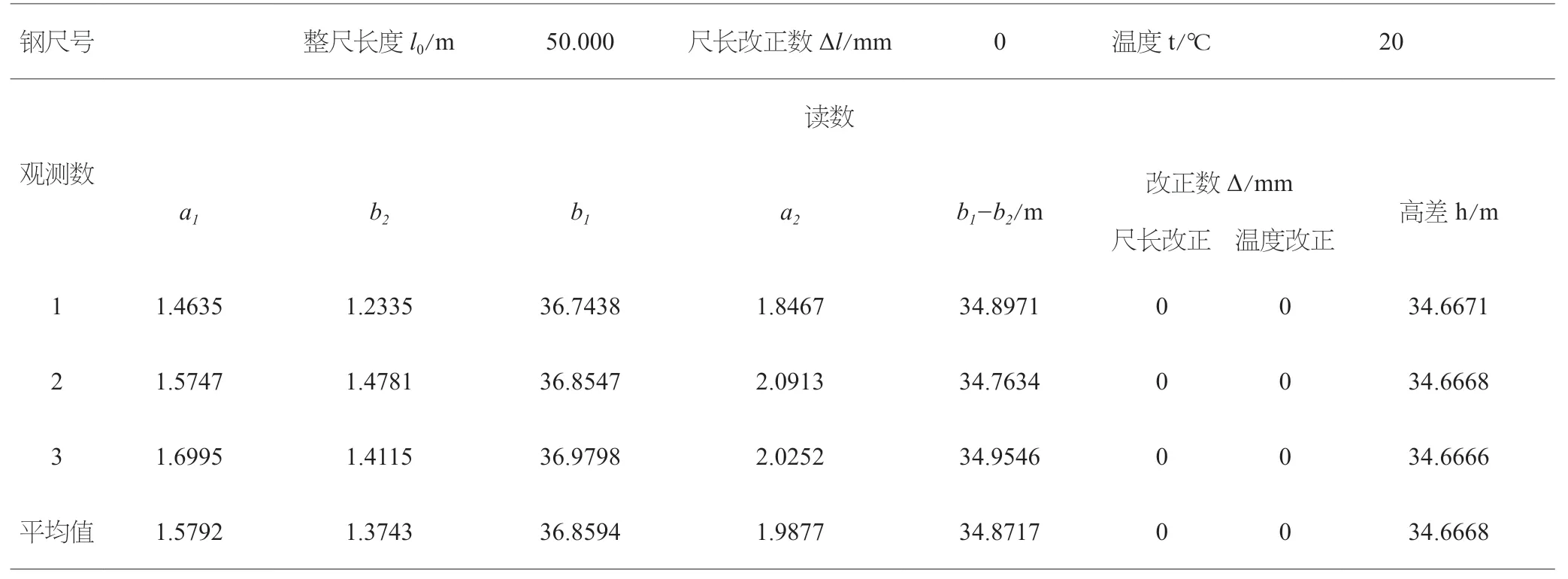
表1 高程传递实测值及解算过程

从表中看出，测回间高差较差小于3mm，精度满足要求，同时该井深小于50m，高差经过温度和尺长改正后，不用进行钢尺自重张力改正。

5 工程实例

石家庄地铁3 号线东段起于石家庄站后止于三教堂接二期，全程一共七站七区间。从上面东王站实例得出如下结论：联系三角形中两根钢丝的间距C 应尽量长，角∝、γ 及β、γ角度布设越小越好，为了达到较高精度，均宜小于1°；联系三角形中及值越小越好，宜小于1.5；联系三角形宜选择直伸形三角形，以减少量边误差对传递角的影响，同时在传递角度时；尽可能地增大两悬挂垂线的间距；此法比较适合开口大深度较深的情况。

根据三教堂站实例了解到两井定向法是两个竖井中分部悬挂一根钢丝，与一井定向相比，减少了投点误差引起的方向差，有利于提高精度，外业施测也方便；悬挂的钢丝宜选用直径0.3mm，底部悬挂10kg 的重锤浸没在阻尼液中；边长尽量采用电磁波测距仪测量，每次独立测三次，各测回较差小于1mm；角度应独立观测六测回，测角中误差应在±1″；此法比较适用于井口小且有两个较长距离的竖井。

6 结语

通过竖井进行联系测量，将地面控制点的方向、坐标和高程精确地传递到地下竖井底部，使地面和地下的控制纳入同一基准中，为地下控制测量提供依据。

综上所述，两井定向的精度优于一井定向，如果在条件允许的情况下，导线直接传导是目前常用方法中精度最好控制的一种平面坐标传导途径，假如项目自身条件允许可以采购陀螺仪全站仪加以复核验证，这样对地下控制系统的精度很大程度上有较大的提升。