柔性直流输电功率模块电容的在线监测

任成林，周竞宇，翁海清，王国强

(1. 中国南方电网超高压输电公司，广州510620；2. 荣信汇科电气技术有限责任公司，辽宁 鞍山114051)

0 引言

模块化多电平拓扑的柔性直流输电具有输出谐波小、功率因数快速可控、没有接入系统短路比限制等优点，近年来在输电领域得到了大量应用。典型柔性直流系统中，一个桥臂由数百个功率模块串联而成，功率模块的可靠性直接决定了柔性直流系统的可靠性[1 - 3]。为了提高系统可靠性，需要对柔性直流功率模块的健康状态进行实时监控，并尽量在柔性直流功率模块发生故障前提前预警，减少故障停运的几率。柔性直流功率模块主要包括：直流电容、功率半导体开关及其驱动、高位取能电源、二次板卡等，本文将探讨在阀控中通过日常运行数据对柔性直流功率模块直流电容的容量进行实时监测的方法，以便进一步通过统计方法发现电容容量随时间的明显变化，对功率模块的可能故障进行提前预警，并为柔性直流系统的计划检修提供重点关注目标。

柔性直流工程中采用的电容大都是干式无油电容，内部采用国际通用的金属化聚丙烯薄膜。电容内部填充聚氨酯，外部采用不锈钢外壳，具有自愈性：即便发生局部电压击穿，击穿点附近的金属化电极会被迅速汽化，在击穿点周围形成绝缘圈，从而可以限制故障扩大，保持电容的正常工作。在这个过程中，薄膜电容会损失微小的电容量，随着这种击穿点的增多，其容量将逐渐减小，直到电容失效[4]。另外，由于内部电介质的退化而导致的电容老化，也表现为电容容量逐步降低及等效串联电阻逐步增大。但由于薄膜电容的等效串联电阻明显低于电解电容，实用中测量困难，因此一般用其容量的衰减作为薄膜电容的健康状态指标，典型认为容量衰减2%～5%时，电容到达了其使用寿命[5]。

为了测量电容的等效参数，包括电容容量和等效串联电阻，目前主要的方法大都是依靠测量电容的端电压、流过的电流，并在此基础上估算电容的参数。显然，首先必须对电容进行激励，主要的方案有以下3种。

1)为了估算电容参数，额外注入特定频率的正弦信号，包括高频信号[6 - 7]和低频信号[8 - 10]；

2)设计出特定的充电或放电过程，进行电容参数估算[4, 11 - 14]；

3)换流器进行PWM调制，依靠功率器件开关所产生开关频率信号[3 - 4, 15 - 17]。

获得了包括激励信号的电容端电压和电流之后，进行电容参数估算的主要算法有以下4种。

1)直接计算法，包括用FFT求出特定频率的电压电流正弦向量进行计算[6 - 7, 15, 17]，或拟合出充放电过程的时间常数进行直接计算[4]。

2)基于电路的时域模型，用最小二乘法进行参数估算。这必然涉及对电路中电压或电流的1、2阶导数计算，主要方法包括：用带通滤波器对电压电流进行预处理[8 - 10]，用多项式函数对电压电流波形进行拟合[11]。

3)基于电路的离散时间模型，直接用最小二乘法进行参数估算[4, 12, 13, 16]。

4)以及基于测量数据和电流模型的对比，用非线性优化方法[14]或Kalman滤波方法[17]进行参数估算。

上述方法中，依靠额外注入特定频率激励信号的方法，和依靠充电或放电过程的方法，都会对换流器的正常运行产生影响，不能用于对换流器中电容健康状态的实时监测。而依靠开关频率信号的方法，往往需要对电容端间电压和电流进行高速的采样，如文献[15]针对Buck电路需要进行0.2 μs分辨率的采样，文献[16]针对900 Hz的低频PWM调试，需要进行分辨率6.25 μs的采样。这种采样频率远超过了实际换流器产品中常规硬件的能力，难以应用到实际产品中。同时，复杂的算法也限制了各种方法在实际产品和工程中的应用[5]。

为了在实际柔性直流工程中对功率模块的直流电容进行实时容量估算，从而监测其健康状态，本文将针对实际的柔性直流工程系统，分析最近电平逼近调制下电容容量估算所需的激励信号，并基于阀控所能获得的实时数据，分析其主要误差来源。在此基础上，本文提出了一种简单实用的数据处理方法，应用最小二乘法进行容量观测，并与其他2种文献中的典型方法进行仿真对比，验证了本文所提方法的有效性和准确性。

1 柔性直流系统功率模块电容在线监测的方案

典型柔性直流工程中，换流阀的拓扑结构[18]如图1所示，每个三相换流阀包括6个桥臂，每个桥臂由桥臂电抗及多个功率模块串联而成，其中，功率模块可以采用半桥拓扑结构，或全桥拓扑结构。由于每个桥臂中串联的功率模块数目很多，换流阀一般采用最近电平逼近的调制方式，并通过内部排序结果和桥臂电流方向来确定投入和切除的功率模块，能够在快速响应控保指令的同时，维持桥臂内部的各功率模块直流电压平衡[18]。

图1 柔性直流换流阀拓扑结构Fig.1 Topology of VSC HVDC valve

模块化多电平的拓扑结构决定了每个桥臂的直流电容平均电压上存在工频和2倍工频波动。另外，为了取得换流阀损耗和功率模块电压应力之间的折中，一般不会将桥臂内部各功率模块的直流电压控制到完全相同，而是允许每个功率模块的直流电压在平均值上下一定范围内波动。这样，对每个功率模块来说，其电容电压将包括3部分波动：桥臂平均电容电压的波动，和功率模块自身直流电压围绕桥臂平均电压上下的波动，典型波形如图2所示。

图2 柔性直流换流阀功率模块典型波形Fig.2 Typical waveforms of VSC-HVDC power modules

图2从上到下依次为：模块所在桥臂的电流，电流正方向如图1的iarm所示；该桥臂所有功率模块的平均直流电压和1号模块的直流电压；1号模块的投入切除指令。显然，在最近电平逼近调制下，柔性直流换流阀中的桥臂电流和模块电容电压已经为电容容量估算提供了足够的激励信号，并不需要像文献[9]那样额外通过环流注入特殊激励信号。但在实际进行功率模块电容容量估算的过程中，需要考虑阀控测量数据主要误差情况。阀控需要依靠通信得到桥臂电流测量值、功率模块电容电压、功率模块投入切除状态等数据，然后首先进行电容电流的估算，并在此基础上进行电容容量的估算。其中，主要的误差来源有3种。

1)桥臂电流CT的测量误差、功率模块对自身电容电压的测量误差。

2)功率半导体器件驱动死区的影响。高压功率半导体器件的死区一般在10 μs以上，而阀控通过通信能够获得的是功率模块中控制器所发出的功率器件触发指令，并不是功率器件的实际门极脉冲。两者之间相差了门极驱动的死区时间，而且死区的影响随桥臂电流的方向而变化。因此，应该根据当前的桥臂电流方向，对功率器件触发指令进行补偿，估算得到功率器件的实际状态，并在此基础上估算电容电流。

3)由于控制系统各部分的同步误差，所得到的桥臂电流反馈与功率模块触发状态，存在采样时刻偏差，并且该采样时刻偏差一直在缓慢变化。

在目前的柔性直流工程中，不论是桥臂电流的采样结果，还是功率模块的触发指令和状态反馈，都是以光纤编码通信的形式和阀控通信。以柔性直流换流阀A相上桥臂为例，换流阀与阀控(及健康状态监控系统)的通信连接情况如图3所示。阀控主控箱通过光纤以固定控制周期向功率模块发出指令，并以同样的通信周期接受功率模块的反馈状态，包括功率模块中电容电压大小、功率器件的触发状态；而桥臂电流的采样及合并单元则以另外一个独立的周期与阀控通信。

图3 健康状态监控系统与阀控及换流阀的通信连接情况Fig.3 Communication among the health status monitoring system, valve and valve controller

如表1所示，桥臂电流的采样周期与功率模块的通信周期相互独立，没有任何同步措施，所有实际上这两者之间不可能是严格的整数倍关系，必然存在差怕。也就是说，对于阀控接受到的最近一组功率模块开关状态、桥臂电流反馈、电容电压反馈来说，在某些时刻桥臂电流反馈超前了电容电压反馈，某些时刻桥臂电流反馈则落后于电容电压反馈。

表1 电容容量观测实际采样信号的同步关系Tab.1 Synchronous relation of actual sampling signal in capacitance measurement

桥臂电流与电容电压的同步误差，也会导致对电容的等效串联电阻无法准确估算。

在阀控录波及健康状态监控系统中设计了对每个功率模块电容容量的在线估算。

阀控主控箱将最近收到的桥臂电流采样值、功率模块开关状态、功率模块电容电压反馈通过高速光纤定周期发送给阀控录波及健康状态监控系统。在健康状态监控系统中，软件的基本流程如图4所示，每收集5 s的高速光纤数据后，健康状态监控系统暂停接受并丢弃后续数据，进行数据处理和计算。

图4 健康状态监控系统软件流程Fig.4 Flowchart of health status monitoring system software

根据上述误差分析，存在电压和电流采样噪声、桥臂电流和功率模块状态的采样同步误差的情况下，图4中的容量估算算法必须对各种误差不敏感。下节将对几种不同的算法进行仿真比较。

2 最小二乘法电容在线监测方法及仿真比较

当电容上没有固定频率的电压电流激励时，现有的电容参数估算算法，大都是基于最小二乘法及其变形，比如递推的最小二乘法等，其基本原理都是估算电容的参数，使得估算参数和采样数据代入电路方程后的误差的方均根极小。考虑到电路方程中需要对电容电压求导会显著放大采样噪声，影响估算精度，现有的解决方法主要有如下2种。

算法1：直接基于电路的离散时间模型进行推导[4, 12 - 13, 16]。

设电容两端电压为vc， 电容电流为ic， 下标n表示第n个控制周期的采样结果，有：

(1)

式中vc,n+1、vc,n、 (ic,n+1+ic,n)均为测量得到的已知数据，所以可以依靠最小二乘法，针对

vc,n+1=k1×vc,n+k2×(ic,n+1+ic,n)

(2)

算法2：对所有的电压电流信号进行带通滤波，只关注特定频带范围内的有效信号。

设电容两端电压为vc， 电容电流为ic， 有：

(3)

显然，将vc和ic通过同一个带通滤波后，式(3)依然成立，设带通滤波函数为BPF(·)， 有

(4)

算法1很容易受采样噪声的影响，而算法2的计算比较复杂，如果嵌入到实时计算中，会明显增加阀控的计算量。因此在研究最近电平调制的特点后，本文提出了第3种算法。

算法3：基于最近电平调制，直接计算电容2次投入之间的电压差和电流积分的方法。

最近电平调制下的柔性直流功率模块中，其电容每充电或放电1～20 ms后，功率模块会被切除1～20 ms，如图2所示。当功率模块被切除时，电容通过并联的放电电阻放电。考虑到电容和放电电阻的放电时间常数在20 min量级上，假设功率模块被切除了10 ms，这10 ms内电容电压降低幅度大约为0.001%，可以忽略。因此，可以实时监测功率模块的投入切除情况，当功率模块处于投入状态时，累计期间电流的积分，同时可以降低电流采样噪声和桥臂电流/电容电压同步误差的影响；当功率模块处于切除状态时，记录并计算期间的电容平均电压，同时能够降低电容电压采样噪声的影响；最终在此基础上，依靠最小二乘法估算电容容量。

如图5所示，设功率模块的第n次投入是从B到C时刻，电容电流等于桥臂电流iarm；而从A到B、从C到D时刻处于切除状态，电容电流为0。

按照上述分析，期间的放电电阻影响可以忽略，因此设：

(5)

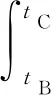
(6)

图5 功率模块电容电流及电压Fig.5 Current and voltage of a power module capacitor

可以基于上述Δvc,n和(icΔt)n应用最小二乘法，进行电容容量C的估算，其中ρ为遗忘因子。

(7)

3 仿真对比验证

研究上述3种方法的精度及对采样噪声、同步误差的敏感程度，基于乌东德柔性直流工程实际参数的仿真结果，并在桥臂电流、功率模块电容电压上分别叠加了最大标准差30 A、20 V的白噪声，以模拟实际系统的采样噪声，对系统中1个桥臂216个功率模块，3种方法的估算结果如图6—7所示。其中系统实际的功率模块电容容量为18 mF。

图6所示为不同同步误差情况下(采样噪声为0时)，对柔性直流换流阀一个桥臂的电容容量的估算情况，用箱形图表示估算结果分布。显然，当同步误差为0时，所有的算法估算结果都很准确，严格为18 mF。同步误差主要影响了估算结果的平均值偏差。随着同步误差的上升，可以看出基于带通滤波的最小二乘法(算法2)的估算偏差明确大于其他两种算法，说明算法2对同步误差比较敏感，如果应用在柔性直流工程中，需要尽量解决桥臂电流测量与功率模块内部控制的同步问题。

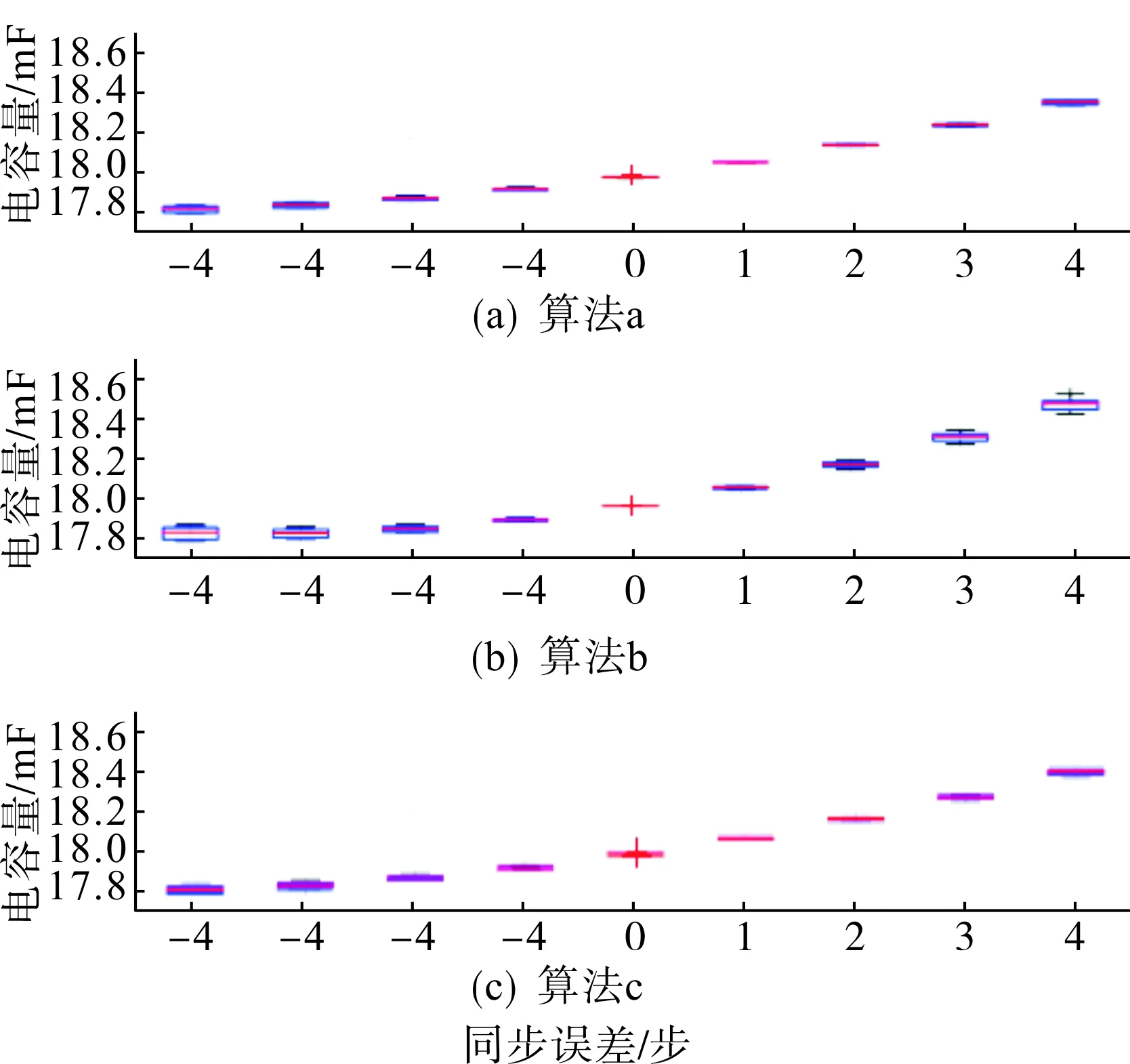
图6 电容量估算的结果分布随同步误差的变化Fig.6 Distribution of the capacitance estimation results with synchronization error

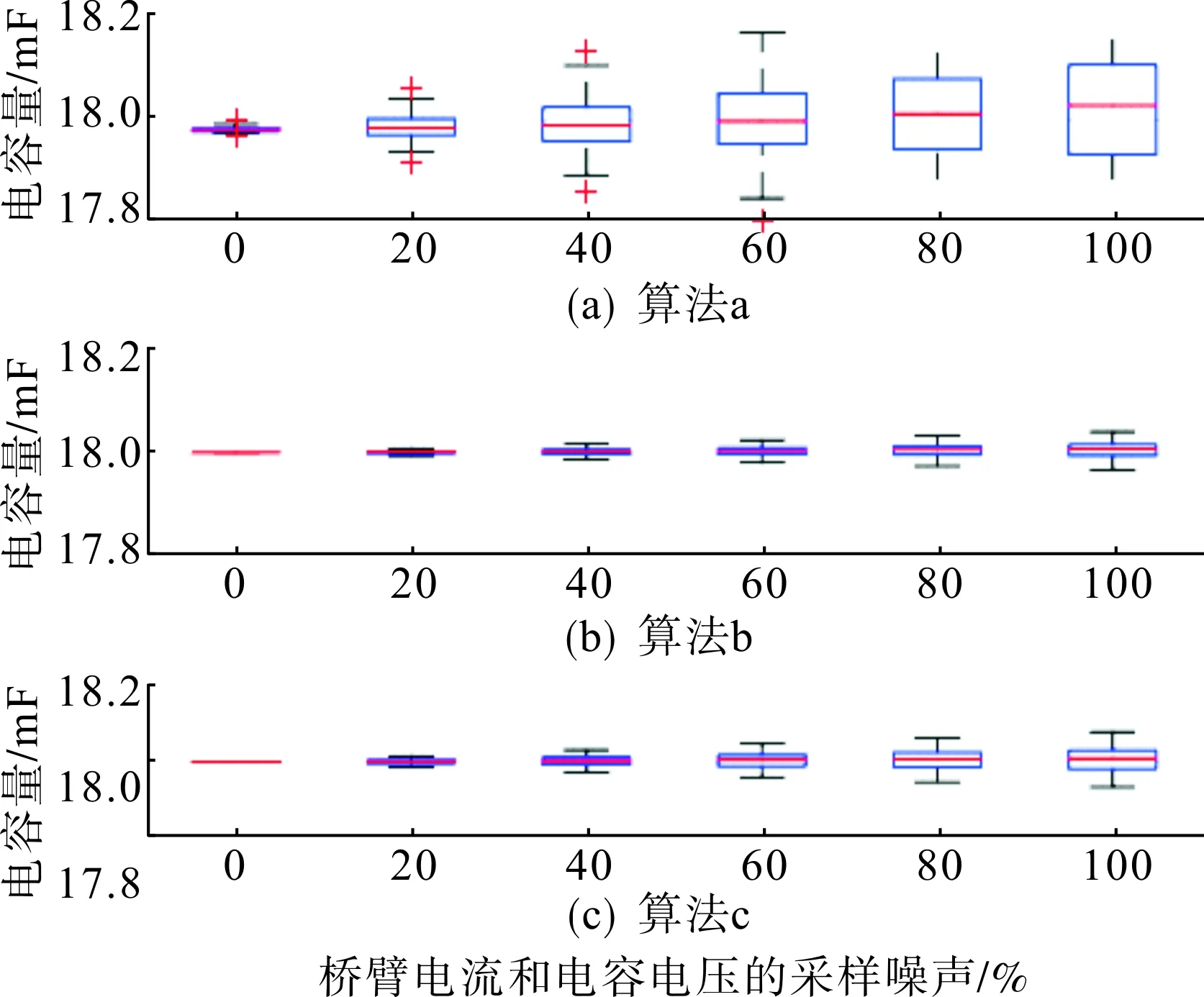
图7 电容量估算的结果分布随采样噪声的变化Fig.7 Distribution of capacitance estimation results with measurement noise

图7所示为不同采样噪声情况下(同步误差为0时)，对柔性直流换流阀一个桥臂的电容容量的估算情况，用箱形图表示估算结果分布。显然，当采样噪声为0时，所有的算法估算结果都很准确，严格为18 mF。采样噪声主要影响了估算结果的分散性。随着采样噪声的上升，可以看出基于直接离散模型的最小二乘法(算法1)的估算结果非常分散，说明算法1对采样噪声比较敏感。考虑到实际系统中采样精度有限，而且电磁干扰的噪声不可避免，算法1不适用应用于实际柔性直流工程。

从仿真结果可以看出，本文提出的针对功率模块投切情况分段计算电容电压平均值和电流积分的方法，对采样噪声和同步误差都不太敏感，而且算法简单，适合在柔性直流系统中应用。

4 工程试验验证

为了验证所提算法的实用性，我们基于某兆瓦级已投运柔性直流工程北通道单元1的A相上桥臂实时录波数据进行了计算，包括1个桥臂的所有397个功率模块的电容容量估算。计算所用的数据包括：1) 阀控所收到的控制用桥臂电流采样值，周期为100 μs；2) 阀控从功率模块接受到的模块触发状态、模块电容电压值，周期为50 μs。

基于该工程进行容值估算的主要误差来源如下。

1)桥臂电流采样(电流传感器及相应采样、处理电路)的误差和噪声；

2)电容电压采样(高精度分压采样电路)的误差和噪声；

3)桥臂电流、功率模块触发状态、模块电容电压值的同步误差。其中，桥臂电流有固定的采样延时，大约在100 μs，在计算中预先加以补偿。而同步误差无法补偿，将影响最终结果。

计算结果如图8所示，图上每个点对应一个功率模块，其横坐标为出厂测试的电容容量记录，纵坐标为基于现场数据的电容容量估算。具体测试数据分析如下。

图8 电容容量估算的结果与出厂测试结果的对比Fig.8 capacitance estimation results based on field data, and the corresponding factory outgoing quality checking (OQC) record

考虑整个桥臂全部397个功率模块，出厂测试的电容容量的平均值为7.930 mF，基于现场数据估算的电容容量的平均值为7.943 mF，两者相对误差0.16%。说明电容容量的估算基本无偏。从图8可以看出，估算误差明显低于实际工程中电容容量的个体差异。

将基于现场数据估算所得的电容容量与出厂测试数据相减，得到电容容量估算的误差(因为出厂测试的电容表精度较高)，误差分布情况如图9所示。从图中可以看出，基于现场数据的电容容量估算误差在1%以内。考虑到电容容量衰减典型2%～5%作为电容寿命的标志[5]，本文所提算法能够有效区分工程所用各个体电容的差异，能够满足电容健康状态监控的要求。

图9 与出厂测试结果相比较，电容容量估算误差的分布Fig.9 Distribution of capacitance estimation error between on-site estimation results and OQC records

综上所述，本文所提算法精度较高，能够满足柔性直流换流阀健康状态监控对功率模块电容容量检测的要求，实现柔性直流换流阀整个生命周期中对电容老化的实时监测。

由于试验条件限制，目前无法在实际工程中降低通信周期、提高采样频率，上述估算误差中，采样误差、测量同步误差各占比例难以直接验证。考虑到实际测量同步误差一般在1个通信周期左右随机变化，从图6的仿真结果看，其导致的本文所提算法的电容容量估算误差不超过0.4%。因此，图9的估算误差大部分来自采样误差和采样噪声。

5 结论

为了实现对模块化多电平拓扑柔性直流换流器中所有的功率模块电容进行容量在线估算，本文首先分析了典型柔性直流工程的阀控架构和测量数据的主要误差来源，包括电压和电流测量本身的测量误差，以及由于测量系统和阀控主控之间独立进行光纤编码传输所造成的同步误差。基于最近电平调制的特点，设计了在线电容容量估算的方案：首先计算功率模块在每个切除状态下的电容电压平均值和每个投入状态下的桥臂电流积分，然后利用最小二乘法进行在线电容容量估算。

基于乌东德工程的参数开展仿真，比较了不同算法的电容容量估算精度和误差敏感程度。结果表明，采样噪声会导致估算结果出现随机偏差，而同步误差则导致估算结果单向偏离实际值。当系统中采样噪声较大时，本文所提方案与带通滤波+最小二乘法的性能类似，明显优于直接离散模型+最小二乘法的方案；当系统中同步误差较大时，本文所提方案与直接离散模型+最小二乘法的性能类似，明显优于带通滤波+最小二乘法的方案。由此可见，本文所提方法对实际误差不敏感，算法简单计算量小，能适用于实际柔性直流工程。最后，通过一个兆瓦级工程的现场数据计算了一个桥臂上所有功率模块电容的容量估算，并与出厂试验时的记录进行了对比，验证了所提方案的准确性。