任意形状热夹杂位移场的三角形单元离散算法1)

侯佳卉 李璞 黎江林 金晓清

(重庆大学机械传动国家重点实验室,重庆 400040)

引言

随着科学技术水平的日益发展,无论在航空航天、武器装备领域,还是在汽车零部件等普通工程应用领域,对于材料的综合性能要求越来越高[1].大多数复合材料在制造装配过程中,其内部普遍存在热膨胀、塑性变形、错配、位错、相变等非弹性变形,美国学者Mura[2]将与之引起的相应非弹性应变统称为“本征应变”.如果本征应变只存在于基体的某局部区域,力学家Eshelby[3]将该区域命名为“夹杂”.Eshelby 夹杂问题[4]是固体力学中的一个经典课题,我国力学工作者在夹杂及其相关问题上的研究也取得丰硕成果[5-10].

夹杂问题在固体力学及材料科学领域具有广泛应用.在真实的工程零部件材料中,夹杂形状各异,不规则形状夹杂的解析解通常不易获得.1961 年Eshelby[3]完成了无限大基体材料中椭球夹杂问题的开创性工作,并提出经典的Eshelby 张量.此后,椭球/椭圆形夹杂得到国内外学者的广泛研究[11-15].Ju和Sun[11]基于Eshelby 张量,通过引入虚拟椭球外单位法向矢量提出了外场点应变的一种类张量表示公式.基于Ju 和Sun 的成果,Jin 等[12]推导了二维平面应变下椭圆柱夹杂外部弹性场的封闭解.随后Jin 研究组[13]给出了三维椭球夹杂的弹性场完备解,系统解决了夹杂内外场的位移、位移梯度、应力、应变等四类Eshelby 张量显式解析解;通过三维向二维问题的转化,可获得二维椭圆柱内外场位移解析解[14].

应该指出,带有尖锐角点的夹杂往往具有与椭球/椭圆迥异的性能,其相关研究也受到研究者广泛关注.例如陶瓷基复合材料中的SiC 纤维横截面呈六边形形状[16]、超导复合材料中的共晶呈多边形[17]、基体中的量子点通常为多面体形状[18],故多边形夹杂更适合模拟此类问题.针对多边形夹杂的研究,Chiu[19]求解了矩形夹杂在弹性层中受到均匀本征应变的应力场问题,并获得其封闭形式解.Rodin[20]提出了二维平面多边形和三维空间多面体夹杂Eshelby 张量的算法.Nozaki 和Taya[21]通过将二维多边形面积分转化为沿单位圆的线积分,研究了具有均匀本征应变的任意凸多边形夹杂的弹性场.基于解析延拓和保角映射,Ru[22]提出了任意形状夹杂在平面/半平面的解析方法,然而在映射函数包含无穷项时,该方法在实际应用中需截断为有限项,因而只能给出近似解,也无法讨论在夹杂角点处的奇异性.周青华等[23]提出一种基于矩形单元的数值化计算方法,借助数值等效夹杂方法,解决了二维平面任意形状杂质问题.

即便是二维问题,夹杂模型通常涉及复杂的计算公式.其中各向同性受均匀热膨胀本征应变(文献中称之为热夹杂) 的问题因其相关计算公式相对较简洁而广受研究者关注[24-26].热夹杂模型在实际工程与研究中也有重要应用,例如可以用来分析量子线[27-28]与基体之间的晶格失配及应变松弛,还可用于模拟孔隙压力,处理相关的地质学问题等[29-30].

利用热夹杂模型,Faux 等[31]基于格林函数方法,通过围道积分获得了线单元和圆弧单元的应力解.鉴于位移解是完备弹性场解的一个重要组成部分[14],并且位移场解也可以作为通过求导计算应变,进而通过胡克定律得出应力的计算起点,因而在弹性力学分析中具有重要的地位.本文的研究可视为对Faux 等[31]的必要补充.Nakasone 等[32]提出了基于三角形单元的数值等效夹杂方法(NEIM),但是他们的算法在三角形夹杂顶点处存在应力奇异,给数值编程计算带来处理上的困难.相对应力/应变结果,本文分析表明位移场在多边形角点处不存在奇异性,因而具有理论分析上良好的光滑连续性与编程计算上的数值稳定性.

本文提出二维平面下任意形状热夹杂位移解的三角形单元离散算法.借助围道积分,给出了夹杂边界线单元所引起位移贡献的解析解.在均匀分布热本征应变情况下:本文研究可直接得出任意多边形夹杂的位移场封闭解,而针对不规则形状夹杂只需对其边界进行离散,计算简便且效率提高显著.在现有文献中,大多数算法是采用均匀的矩形单元网格[23,33]离散夹杂区域,因而即便对于均匀本征应变情况,也需进行二维离散,造成计算浪费.本文提出的三角形单元离散法可用于非均匀本征热应变情况.当受非均匀分布本征应变时,夹杂区域可数值离散为足够精细的三角形单元,进而利用叠加原理获得原夹杂所产生位移场的数值解.

1 任意形状热夹杂位移解数值化方法

1.1 均匀本征应变下热夹杂位移解

本文所有变量均定义在笛卡尔坐标系中.假设在平面应变条件下,无限大平面基体内嵌有任意形状夹杂Ω,其内部有均匀分布的本征应变(图1).夹杂与基体为各向同性,且具有相同弹性常数Cijkl

式中,µ为剪切模量,ν 为泊松比,δij为Kronecker delta符号.

夹杂问题可以借助“激励−响应”机制[34]进行求解.在激励点X′(ξ,η)施加沿j方向单位集中力时,响应点X(x,y)在i方向产生的位移定义为格林函数Gij(X−X′).针对二维全平面问题,为方便计算其具体表达式[2]可写成如下形式

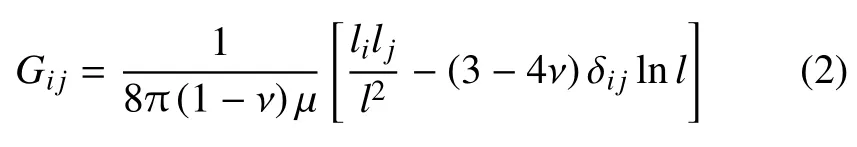
图1 分布有均匀本征应变的夹杂示意图Fig.1 Schematic diagram of inclusion with uniformly distributed eigenstrains

式中,l是响应点X(x,y) 与激励点X′(ξ,η) 的相对距离:l2=其中l1=x−ξ,l2=y−η.利用体力法[2],二维全平面夹杂问题的位移解可以表示为

为了便于表示及计算机编程,引入基于Voigt 记号[14]的矩阵形式:位移和本征应变分别用[u1,u2]T和表示.本文考虑本征应变均匀分布的热夹杂(即0),此时式(3)为

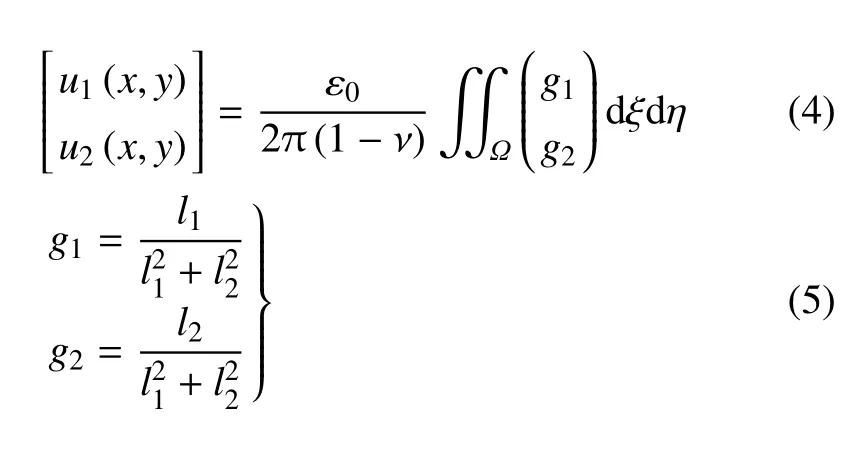
应用格林定理,式(4)中的面积分可转化为沿闭合曲线边界∂Ω(如图1 所示)的围道积分

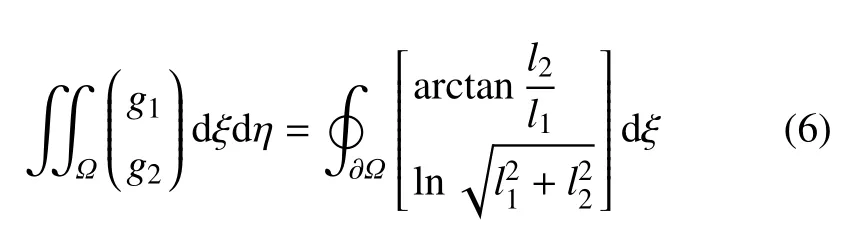
为进一步求解式(6),将夹杂边界数值离散为线单元,如图2 所示,设一个典型线单元L的两个端点分别为(x1,y1),(x2,y2),任意位置(可以位于夹杂内部或外部)响应点记为(x0,y0).经过一系列代数运算和简化推导,式(6)右端在该线单元上的积分结果可写成如下形式的封闭解

图2 夹杂边界离散示意图Fig.2 Discretization of the inclusion boundary by line elements

任意形状夹杂的边界都可用多边形进行数值离散近似,进而基于线单元解的迭加可获得最终的解析解,从而解决任意形状夹杂产生的位移影响.本文封闭解以线单元的顶点坐标作为输入参量,提供了一种高效且便于计算机上实现的数值计算方法.

1.2 顶点奇异性分析

现有文献[20,32]指出,应变/应力解在多边形顶点处具有奇异性,从而带来实际应用中数值处理上的困难,此类由于奇异性造成的计算编程的数值稳定性问题在文献[34]中有相关讨论.作为对比,现考察本文线单元所贡献位移解的奇异性.当响应点(x0,y0)无限靠近线单元L的端点(x2,y2)时,线单元封闭解式(7)简化为

式(8) 结果表示在线单元两个顶点处位移结果是有界且连续的,说明位移解在线单元端点处不产生奇异性(这与应变/应力解迥然不同).此外,与本文算法相比,常见的限元方法在处理角点(几何不连续)处的位移通常需要极其精密的网格,且往往精度较差.本文算法基于线单元,数值离散实施较易,在计算分析中可带来极大便利.

1.3 三角形夹杂单元离散算法

在非均匀温升问题中,夹杂内部受非均匀分布的热本征应变.基于本文均匀热本征应变下的线单元贡献解,可进一步提出如下数值算法:将待求解的夹杂区域离散为三角形基本单元,见图3.当三角形单元足够精细时,则可近似假定每个单元内部分布均匀本征应变(可取其重心点处本征应变为计算值).通过1.1 节结果利用线单元解的迭加,可以得出三角形单元的位移贡献.进而基于夹杂问题的线性性质,通过离散的三角形单元解的迭加,可求得受任意分布热本征应变任意形状平面夹杂问题位移场的数值解.在处理此类问题时,本文方法只需在夹杂域内进行离散,而有限元方法则要同时对无限大基体进行离散,造成计算量的增加和时间成本的浪费.

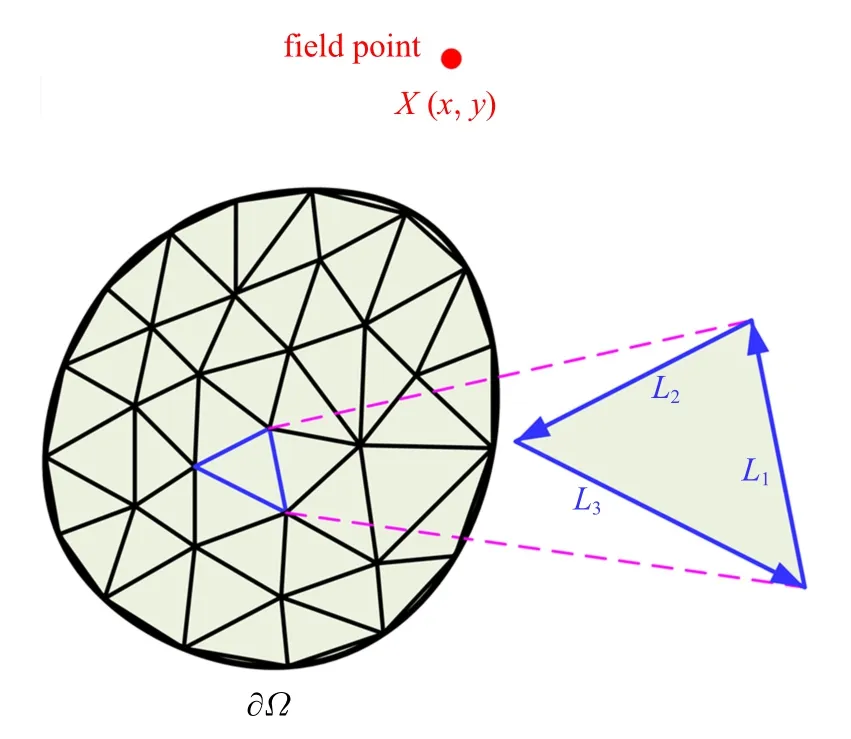
图3 夹杂区域三角形离散Fig.3 Triangular discretization of inclusion region

在实际计算中,夹杂区域的三角形离散可结合有限元软件如ABAQUS 完成.在ABAQUS 中提取夹杂模型离散后的三角形单元节点信息,并将其作为输入参数引入程序,利用三角形单元离散算法计算待求目标场点处的位移值.下文中所有数值计算均通过FORTRAN 语言编程实现.

2 数值化方法的实现及验证

2.1 均匀本征应变下热夹杂解验证

如图4 所示,利用无限平面介质中的椭圆热夹杂模型作为实例验证位移解的有效性.如1.1 节所述,均匀本征应变下只需离散边界,通过对比分析(见表1),离散线单元数m取50 时,既能保证计算精度(相对误差大致处于0.2%范围),又有较好的运行效率,所以本节算例模型边界均离散为50 个线单元.设a1,a2分别为椭圆形的长、短半轴,定义形状参数为γ=a2/a1.本文拟采取Ti-6Al-4V 材料为研究对象,其杨氏模量E为110GPa,泊松比ν 为0.34,取ε0=1.0×10−3,验证夹杂对基体位移场的扰动影响.

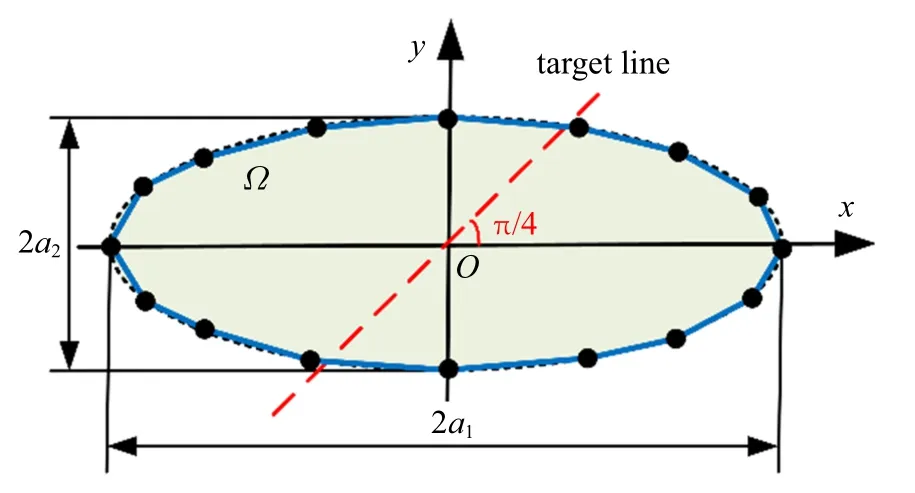
图4 椭圆形夹杂模型Fig.4 Elliptical inclusion model

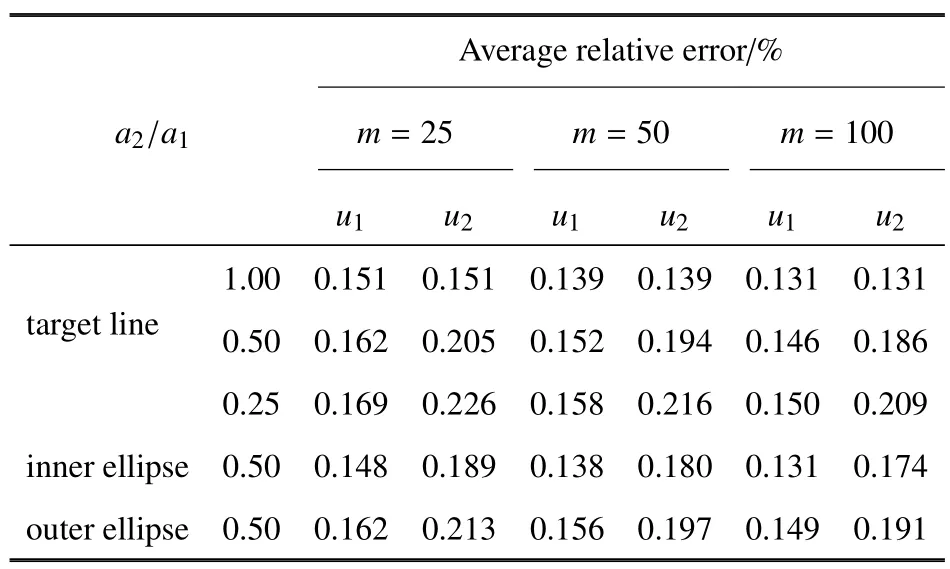
表1 数值解求解得到位移分量与解析解的平均相对误差Table 1 Average relative errors of displacement components obtained by the numerical method compared with those by analytical solution

图5 给出了Ti-6Al-4V 材料在长半径a1=1 不变的情况下,形状参数分别为γ=0.25,0.5,1 时,椭圆夹杂模型引起的沿图4 所示目标线的位移,最终的位移结果通过除以u0=a1ε0×103/[2π(1 −ν)]实现无量纲化.将数值解与解析解[15]进行对比分析.当场点(x,y)位于椭圆内部时(内场解),位移为

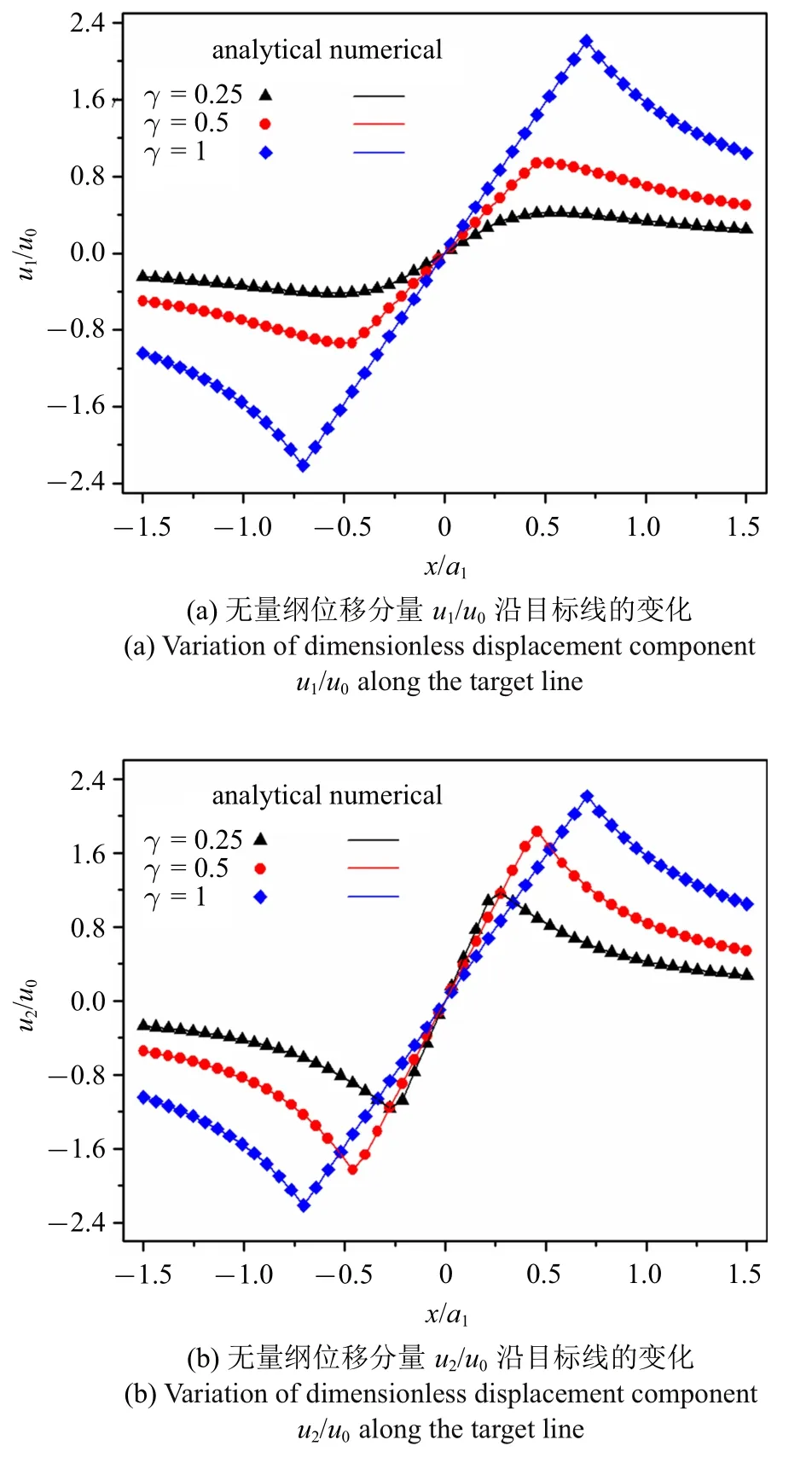
图5 Ti-6Al-4V 材料不同椭圆形夹杂沿目标线的位移Fig.5 The displacement along the target line for various Ti-6Al-4V inclusions in elliptical shape

而外场位移解析解为

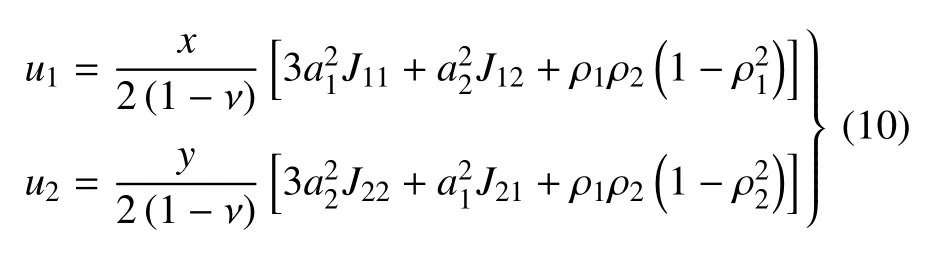
式(10)中J11,J12,J21,J22,ρ1,ρ2的具体表达式见附录.由图观察可知,含有均匀本征应变的热夹杂引起夹杂附近基体位移场的扰动,且位移场在夹杂内部呈线性分布,与三维的椭球夹杂位移解[13]情况一致.因为应变可由位移求导获得,由之可以推断椭圆夹杂内部总应变为均匀分布,此即Eshelby 夹杂的经典结论[3].随着形状参数γ 的增大,产生的位移影响增大,在内外场边界处,位移分量连续;在夹杂外部,位移分量随x轴坐标的增大而减小,并与解析解结果吻合.

进一步,在形状参数γ 为0.5 的情况下,将现有方法求得的结果与解析解得到的沿共焦椭圆(图6)产生的位移结果进行比较,位移结果如图7 所示.

图6 椭圆形状参数为0.5 时内外共焦椭圆模型Fig.6 Inner and outer confocal elliptical models with aspect ratio γ=0.5

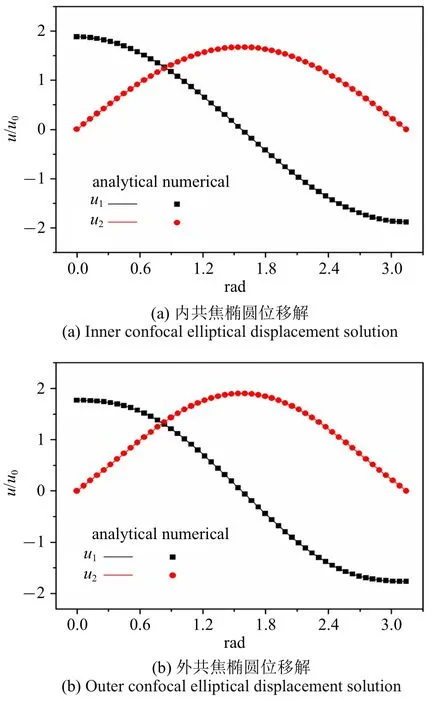
图7 Ti-6Al-4V 材料在夹杂椭圆形状参数为0.5 时内外共焦椭圆位移解Fig.7 Displacement solution of internal and external confocal ellipse of Ti-6Al-4V material with aspect ratio γ=0.5

由于位移u1和u2分别关于x轴对称/反对称,此处只给出θ 取0～π 范围的位移结果对比.通过观察可知,数值解与位移解两种方法较好的保持了一致性,从而验证了数值法的有效性.

为进行定量误差分析,定义平均相对误差如下

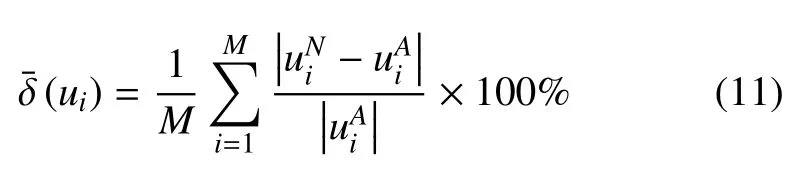
2.2 非均匀本征应变下热夹杂解验证

为说明数值法对于非均匀本征应变下热夹杂问题的处理能力.考虑含于无限大平面内的圆形热夹杂.如图8 所示,其半径为a,以该圆形夹杂的中心为坐标原点,夹杂内部分布有线性本征应变ε0ξ.最终的位移结果通过u0=aε0/[2π(1 −ν)]无量纲化,图9 给出了本文数值解与FEM 求解得到的圆形热夹杂模型沿图8 所示目标线方向位移分布图,由图可见,在外场时,夹杂产生的位移影响随着x轴的增大而减小,且逐渐趋于0.两种方法所得结果吻合良好,验证了本文数值方法处理非均匀分布本征应变的有效性.

本文算法对不规则形状热夹杂同样适用.如图10(a) 所示,存在于无限大平面的半椭圆热夹杂,其椭圆形状参数γ=0.5,初始本征应变设为最终的位移结果通过u0=a1ε0/[2π(1 −ν)]无量纲化,目标线取x轴.对于不规则形状夹杂问题,通常不易得到其解析解,再加上本征应变为线性分布,其解析解更加难以获得,而本文所提出的数值计算方法可有效解决这些难点.把夹杂区域用三角形单元进行离散,计算网格见图10(a).利用本文算法获取的位移结果与FEM 比较,如图10(b)所示.通过观察可知位移分量在夹杂边界处连续,且随着外场点逐渐远离中心点,位移分量渐渐趋于0.数值计算方法与FEM 结果保持了良好的一致性,由此验证了数值计算方法处理非均匀本征应变下不规则形状热夹杂问题的能力.

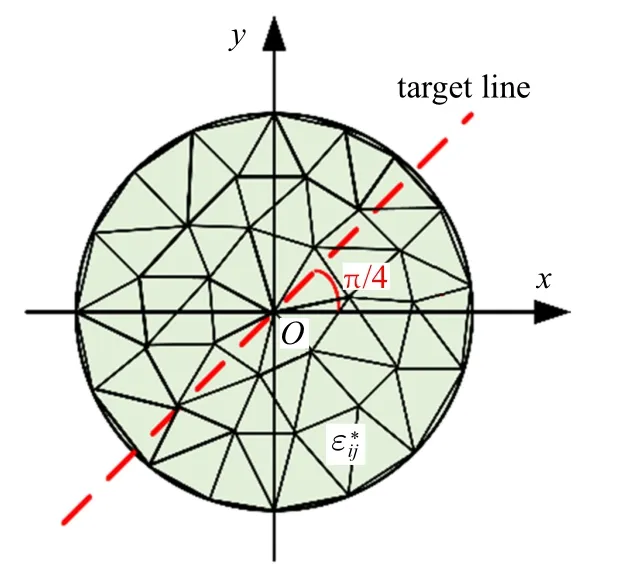
图8 圆形夹杂模型示意图Fig.8 Schematic diagram of circular inclusion model

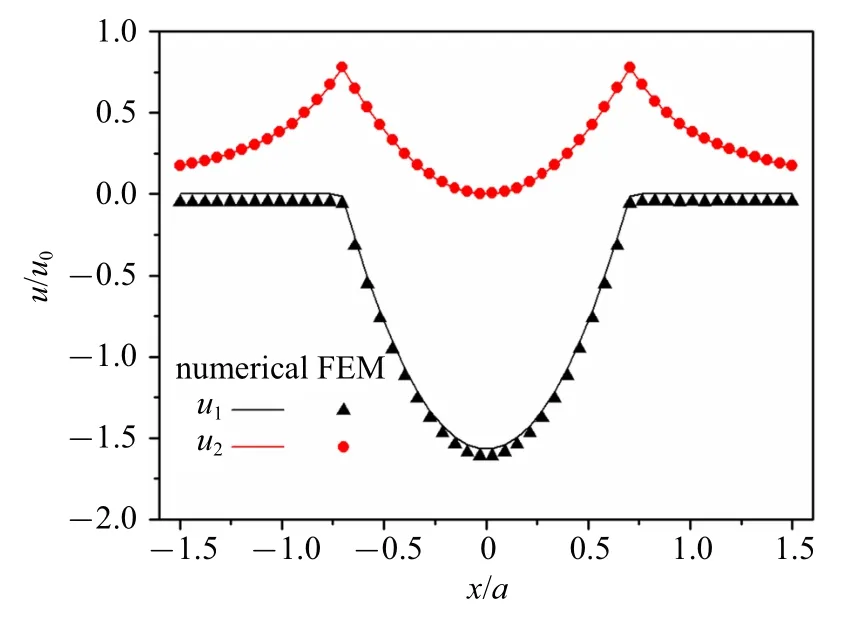
图9 圆形热夹杂在线性本征应变下的位移验证Fig.9 Verification of the displacement for thermal inclusion with linear eigenstrain

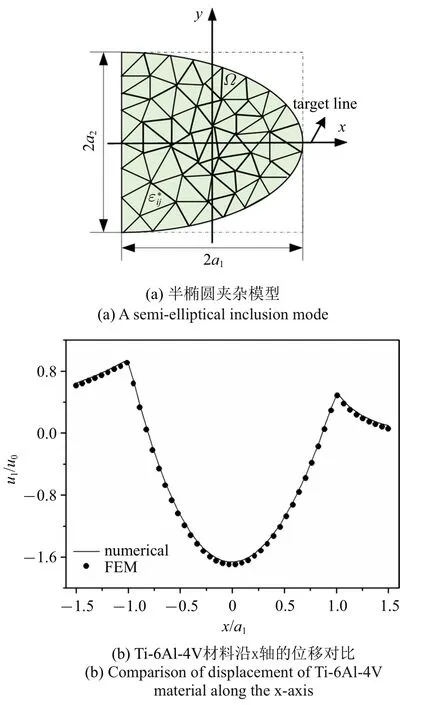
图10 不同方法求解半椭圆形热夹杂模型所得结果比较Fig.10 Comparative study on thermal inclusion of semi-elliptic shape solved by different methods

3 结论

提出一种数值化计算方法,用以处理二维任意形状夹杂位移问题.主要得到如下结论:(1) 推导得到基本线单元的位移解形式,与应力/应变解不同,本文所提出的位移解在多边形夹杂顶点处并无奇异性;(2)对于均匀本征应变下任意形状热夹杂问题,通过边界线离散化,可基于线单元解求解位移场;对于非均匀本征应变问题,可将夹杂区域离散为三角形单元进行求解;(3)利用椭圆、圆形与半椭圆形热夹杂的算例验证本文所提数值计算方法对于任意形状热夹杂问题的处理能力,结果得到了较好的验证.

附 录

附录式(10)相关参数表达式

设a1,a2分别为椭圆形的长、短半轴,当场点X(x,y)位于椭圆外部时(即>1)