多参数协同调制的高分辨力直线时栅位移传感器

贺 鹏，鲁 进,2，张兴红，张天恒，谢述祥

(1.重庆理工大学，机械检测技术与装备教育部工程研究中心，时栅传感及先进检测技术重庆市重点实验室，重庆 400054；2.重庆理工大学机械工程学院，重庆 400054)

0 引言

直线位移传感器对工业、农业、国防等各领域有着重要的意义，关系到科技的进步与发展，所以直线位移传感器越来越多地受到各国家的重视[1]。而目前大多数直线位移测量很难满足在实现高分辨力测量的同时也能实现高精度、大量程范围的测量，少数的直线位移测量实现了大量程高分辨力的测量，但价格昂贵且对环境要求十分严格。

现在，直线位移传感器精度最高的是激光干涉仪，在几m的范围可以实现1 μm的测量精度，但对光学介质敏感、体积大[2]；光栅能够在500 mm内实现1 nm的分辨率，但是采用光学测量方法的仪器价格昂贵[3-6];文献[7]中采用电学测量方法，压阻传感器可在1～500 μm实现的测量精度为0.49 nm，但绝对精度受温度的影响较大。文献[8]采用标准滚针变磁阻，对传感器的有效半径和磁路气隙长度进行优化，但滚针的设计难以保证绕线的均匀性和一致性，从而影响位移测量精度。文献[9]提出了一种基于PCB技术与时栅测量技术相结合的位移传感器，然而空间的分辨力还是受限于激励线圈和感应线圈的极距，当极距到达一定极限后，想进一步提高其空间分辨力将变得非常困难。

针对上述问题，本文提出一种基于PCB技术的新型直线时栅位移传感器，通过在PCB基板上布置阵列的激励线圈和特定形状的感应线圈，形成2个完全相同的空间正交的传感单元，在不改变励磁线圈和感应线圈空间极距的情况下，能实现在信号源头将分辨力提高1倍的测量，不依赖于超精密刻线技术，结构简单，极易实现。

1 传感器结构及其工作原理

两参数协同调制的传感器整体结构如图1所示，传感器基体分为2个单元，上下单元完全一样，各单元均由下导磁基体、励磁线圈、感应线圈和运动导磁体组成。回形线圈嵌于下导磁基体的上表面，且回形线圈按照正绕和反绕的形式等间距交错排列，形成整体的定子测头。感应线圈设计成正弦形状，通过改变感应线圈所包围面积的有效磁通来对时间周期信号进行有效的调制，上导磁基体为动测头。上下2个单元在沿X轴方向相互错开W/8，或者将动尺错开W/8(W为空间极距)，从而达到2个单元的空间正交。

利用毕奥-萨伐尔定律[10-11]构造基波磁场分布单匝方形线圈磁感应强度分布函数，从而得到通过不同尺寸的单匝数线圈叠加而成的多匝数方形线圈产生的磁场强度，一段载流直导线AB在P点产生的磁感应强度计算如式(1)所示：

(1)

图1 传感器结构示意图

励磁线圈模型如图2所示。

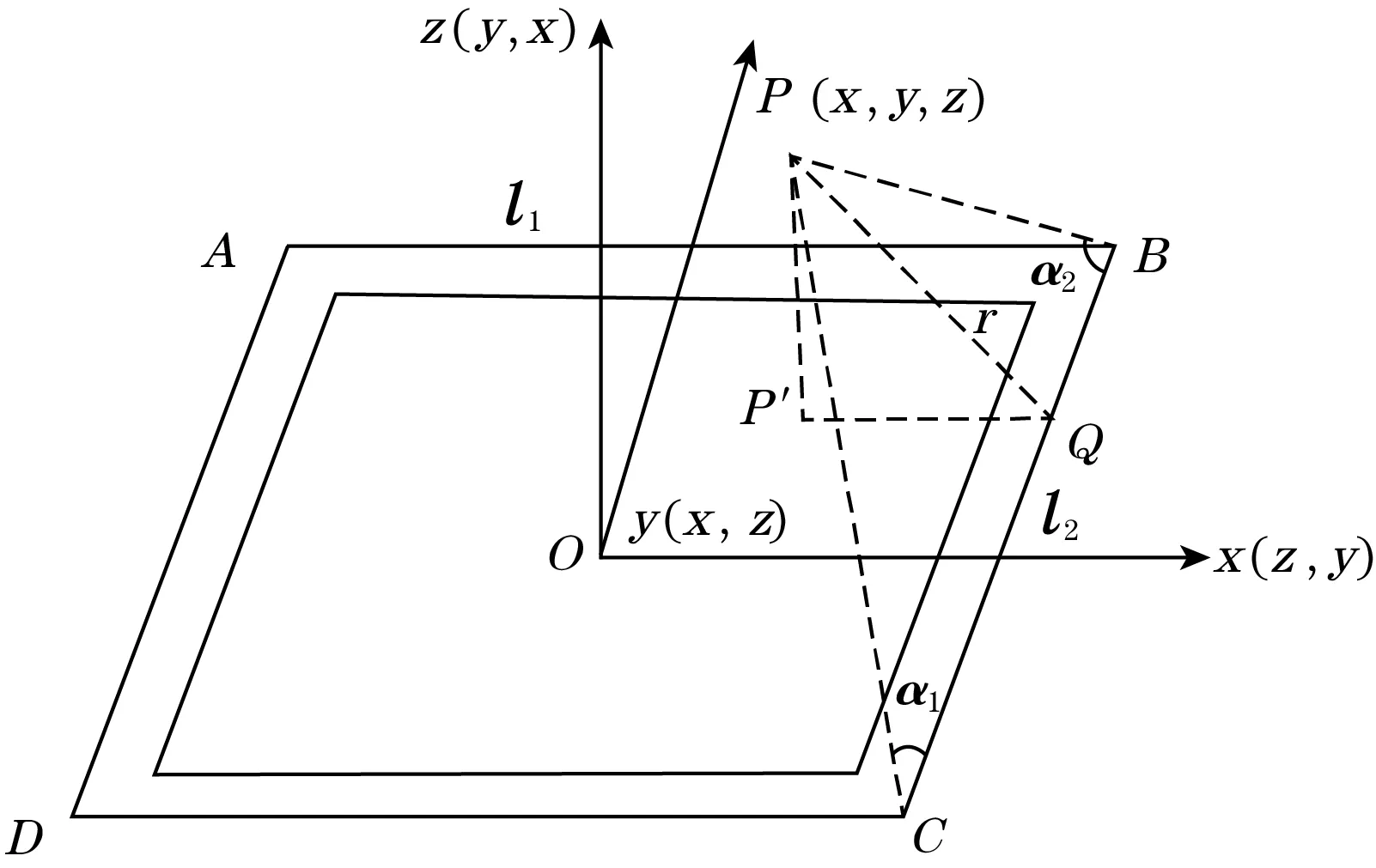
图2 励磁线圈模型

多匝数矩形线圈在场点P(x，y，z)所产生的磁场分布可以是多个不同尺寸的单匝数线圈在该场点P(x，y，z)所产生的磁场强度的叠加，故空间内任意一点磁场强度如式(2)所示：

(2)

式中：i为线圈的匝数；l1i、l2i分别为各线圈的长和宽；n平面线圈的总匝数。

传感器励磁线圈采用2个多匝平面线圈时，组成所需要的磁场分布情况，传感器励磁线圈的结构如图3所示。

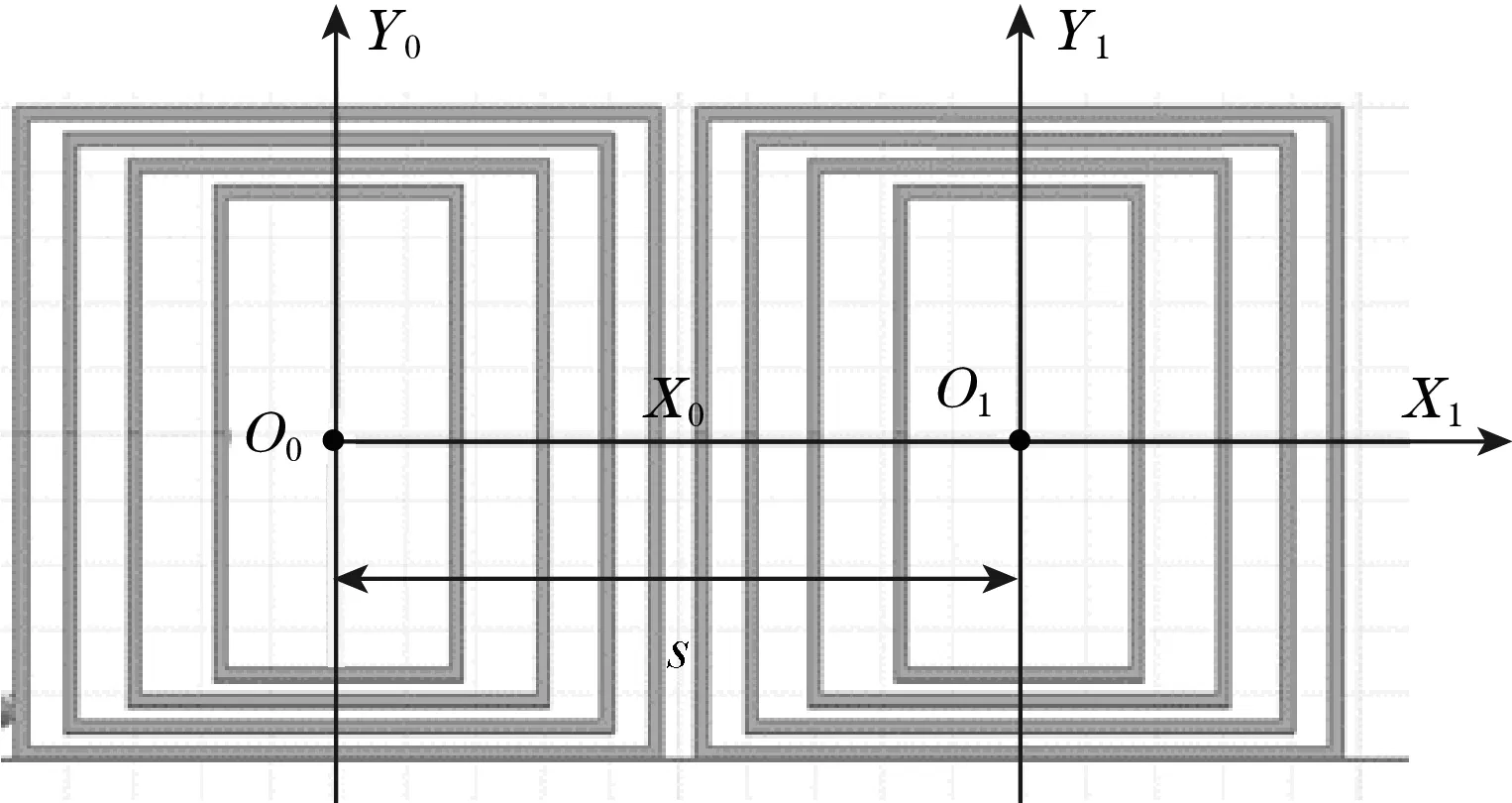
图3 传感器励磁线圈结构图

在水平方向上，将正弦和余弦励磁线圈等间距分布，以初始的励磁线圈为基准，建立初始坐标系X0Y0O0，坐标原点定义在初始励磁线圈的中心点，根据坐标转换原理，以右边线圈中心点建立对应新的坐标系X1Y1O1，其换算关系满足式(3)：

(3)

式中s为2个励磁线圈中心的距离。

从图3可以看出，励磁线圈在X轴方向上变化，换算关系中，横坐标变化，纵坐标不变。

2个励磁线圈是多个矩形线圈产生的磁场强度的叠加，所构造的磁感应强度为

Bz=Bz0+Bz1

(4)

式中：Bz0为初始励磁线圈的磁感应强度；Bz1为右边励磁线圈的磁感应强度。

图4表明了传感单元的励磁线圈和感应线圈的空间位置关系以及2个传感单元的空间位置关系，2个传感单元的激励线圈和感应线圈在空间上错开1/4的空间极距W，2个传感单元空间位置错开W/8。励磁线圈箭头表明了电流的流向，分布于印制电路基板的不同层上，电流的流向也是箭头的方向。

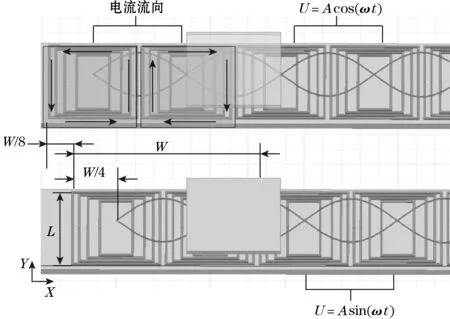
图4 励磁线圈和感应线圈位置关系

当动尺在多匝线圈产生的磁场强度中沿X轴移动时，通过多匝线圈的磁场强度以W为节距呈现周期性变化，在感应线圈所感应的有效磁通面积也呈现周期性变化，当激励电流I1(t)=Asin(ωt)通入到传感单元一中，产生的磁通应用傅里叶级数展开如式(5)所示：

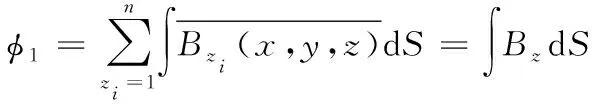
(5)

在只考虑磁通量中基波分量的情况下，磁场的感应线圈的感应电动势为磁通量共同作用的结果，传感单元一的感应电动势如式(6)所示：

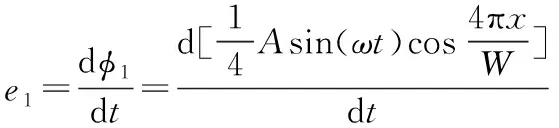
(6)

同理传感单元二所产生的电信号应为

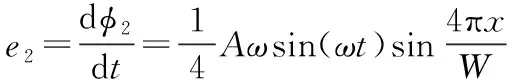
(7)

通过三角函数诱导变换反推出得：

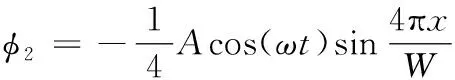
(8)

比较式(5)和式(8)可知，传感单元二是传感单元一沿X轴方向上相差W/8空间极距形成的，在传感单元二中通入电流I2(t)=Acos(ωt)，在两单元共同作用下，产生电行波信号如式(9)所示：

(9)

对输出的行波信号通过整形成为方波信号输入微处理器中。利用高频时钟脉冲实时测量与参考信号的时间差Δt，该时间差与动尺相对于定尺的位移关系如下：

(10)

式中N为动尺相对于定尺所走过的完整极距数。

2 建模仿真与误差分析

2.1 有限元建模仿真

根据传感器原理，采用电磁场有限元软件Ansoft Maxwell进行建模与仿真分析。Maxwell中设置仿真求解器为瞬态电磁场，在理想情况下，选择感应线圈的电阻较大，可以使得感应电动势所流过的电流尽可能减小电磁对模型仿真的干扰，网格划分较精细，励磁线圈和感应线圈的网格设置最大边长取1 mm，导磁基体网格最大边长为5 mm，真空网格为10 mm。根据实际建立的传感器模型结构确定仿真求解参数，传感器结构模型具体基本参数设置如表1所示。

表1 仿真模型参数表

当一个励磁信号作用于一个传感单元，传感器感应线圈会感应出一个驻波信号，如图5(a)、图5(b)所示。当2个励磁信号作用时，2个驻波信号叠加成行波信号，如图5(c)所示。从如图5(c)可看出，当动尺移动一个极距W，该传感器相对于原始信号进行了2倍的细分。故可以使传感器的分辨力在源头提高1倍。

在t=1 μs时刻，传感器模型的磁场分布云图如图6所示，图中左侧磁场强度的大小与理论计算数值接近，磁场的磁感应强度会随着时间变化呈周期性变化。

2.2 误差分析

感应线圈感应的电动势初相角应与位移量成线性关系，将仿真初相角α经过相位与位移转换公式得到位移量δα，并且令起始位置为0，再减去理论位移值δβ，可得到位移测量误差值δ。

(11)

δ=δα-δβ

(12)

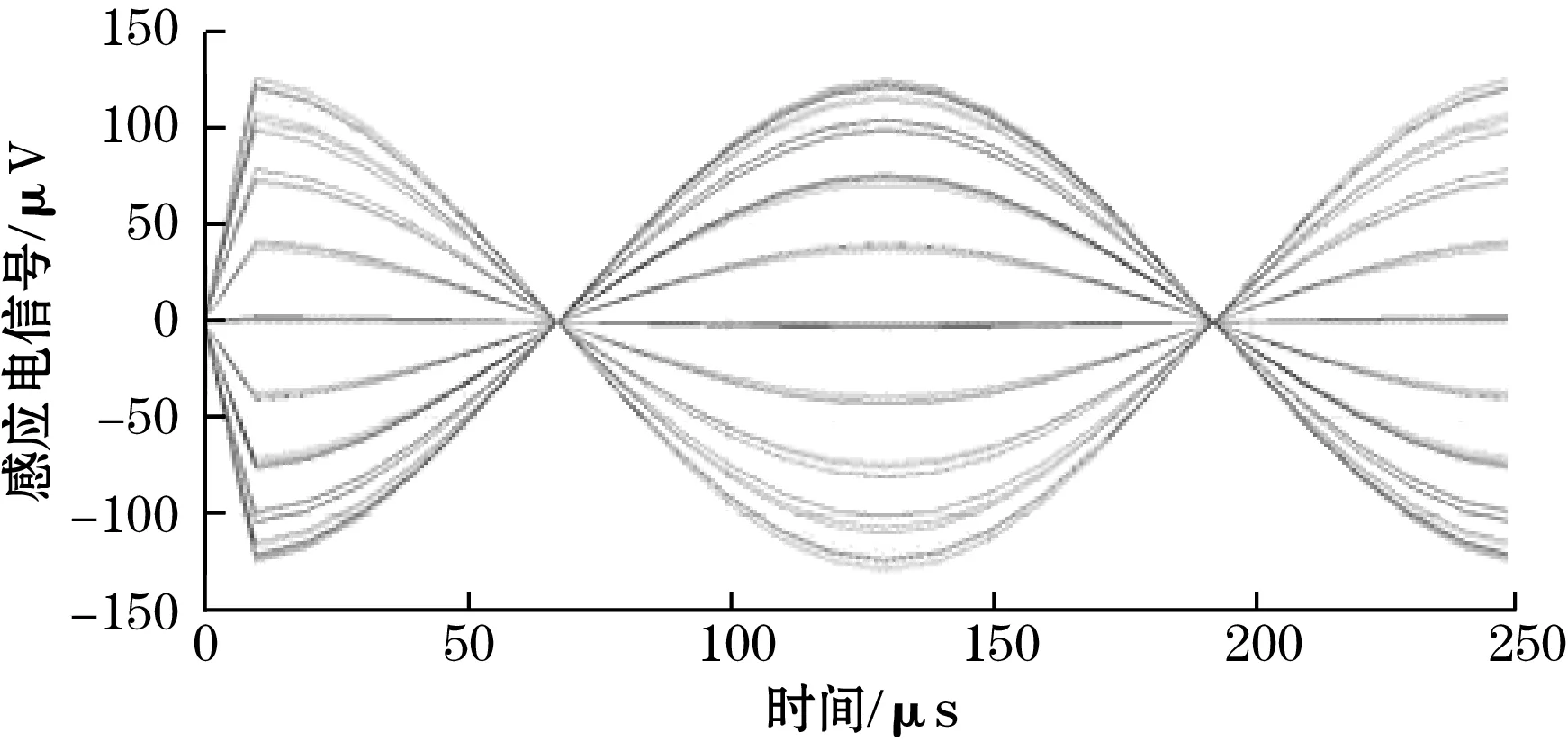
(a)传感单元一磁场感应线圈输出的感应电动势

(b)传感单元二磁场感应线圈输出的感应电动势

(c)两传感单元感应线圈串联输出的感应电动势图5 传感单元一和传感单元二串联输出的感应电动势

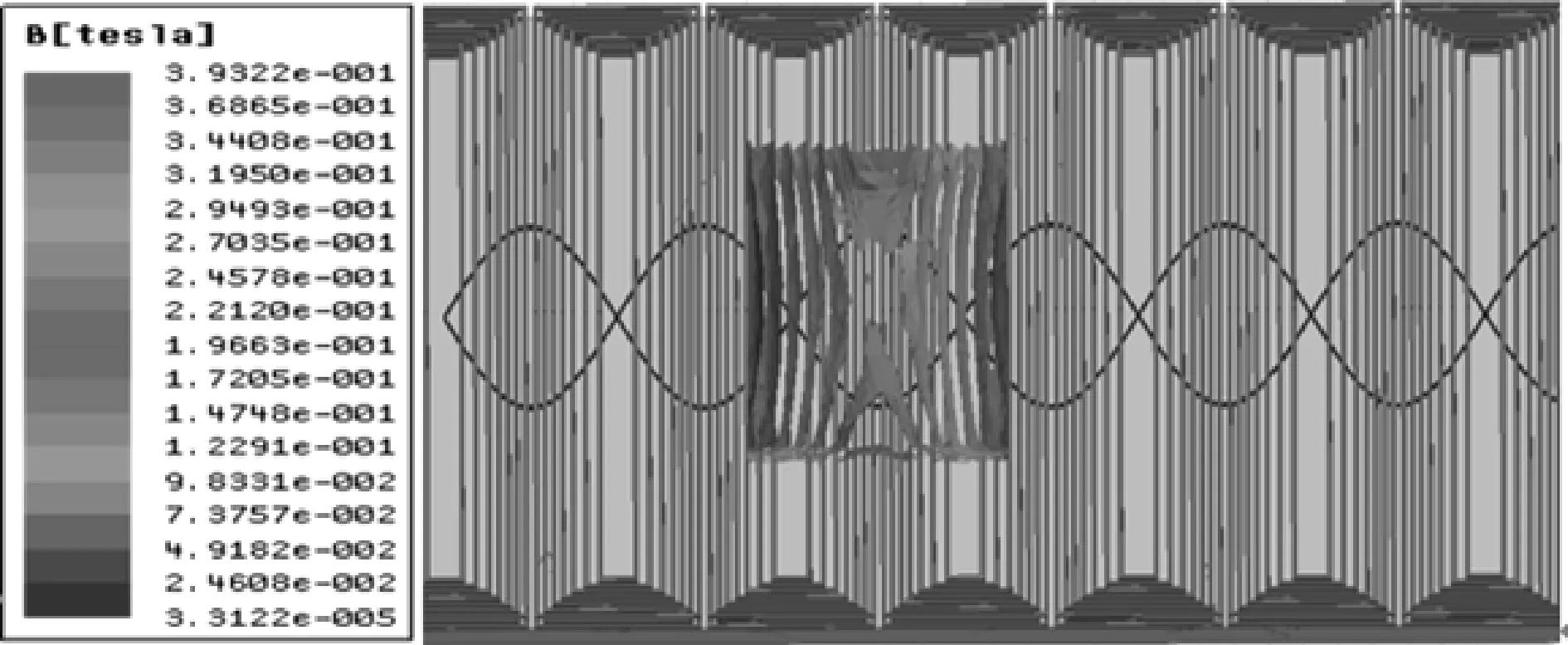
图6 模型磁场分布云图

图7为动尺空间位置的初相角及位移测量误差曲线。由图7可知，仿真曲线的初始相位与理论曲线的初始相位基本重合，将所得位移测量误差曲线进行FFT变换。

图8为位移测量误差频谱分析图。如图8所示，位移测量误差谐波成分主要包含2次、4次、6次误差。通过所得数据，进一步对直线位移传感器电磁仿真结果分析总结如下：

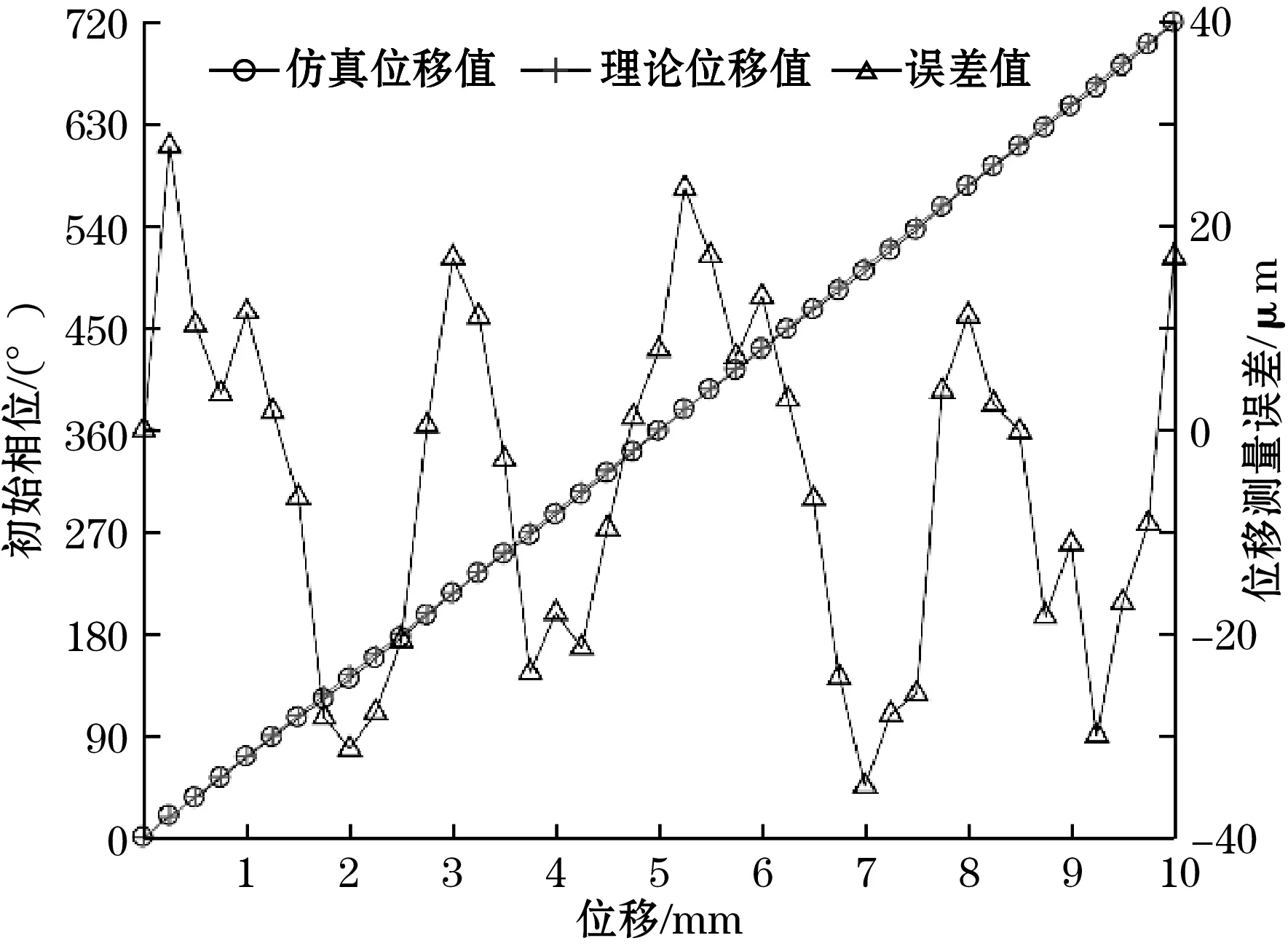
图7 动尺空间位置的初相角及位移测量误差曲线

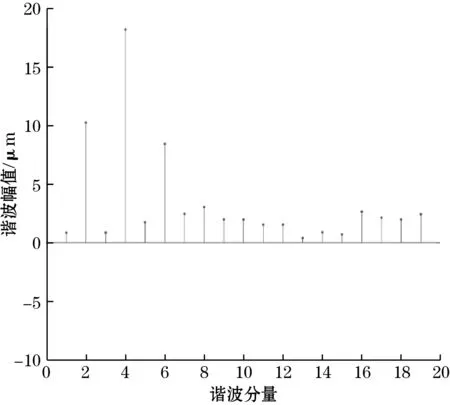
图8 位移测量误差频谱分析图

(1)线圈匝数影响磁场均匀性和磁场强度。单匝线圈所形成的磁场均匀性较差，多个矩形线圈组成“回”型线圈合成的磁场均匀性也会有变化，从分析可知，仿真模型的线圈参数和匝数没有达到理想的值，将会造成2次误差。

(2)在理想情况下，励磁线圈和感应线圈的轨迹应该是一条线，但实际中，由于矩形线宽的影响，不会达到完全理想的情况，这也会引入4次误差。

(3)在使用Maxwell进行磁场分析时，也会引入误差，仿真时网格划分对数据计算的误差对仿真结果产生影响，各次谐波分量是由磁场仿真引入误差。

从位移测量误差曲线图可知，位移测量误差在节距内周期性变化，采用误差修正可以对时栅位移传感器进行谐波修正[12]，进一步减小主要谐波分量。

3 实验验证

经过理论验证与仿真分析，研制传感器样机、搭建实验平台，并对传感器进行测试。

本文采用PCB(printed circuit board)工艺加工研制传感器的线圈，PCB板设置为4层板，样机参数为100 mm×60 mm，板厚为1.6 mm，设计了励磁线圈和感应线圈，为获取较强的感应信号，同时也保证感应线圈在感应信号时实现结构上的对称，设计了2组感应线圈，分别设计在Mid1 Layer和Mid2 Layer层，励磁线圈则布置在Top Layer和Bottom Layer。

对研制的传感器样机进行验证分析，搭建了如图9所示的直线测量实验平台，整套传感器系统的实验平台是安装在经过防震处理的平台上。经过稳定性测试满足实验要求的基础上，使用RENSHAW XL-80激光干涉仪的测量值作为测量基准开展实验。

图9 传感器样机安装与实验平台图

实验时，通过电机控制系统驱动电机带动动尺运动记录采样数据，位移测量误差曲线如图10所示。

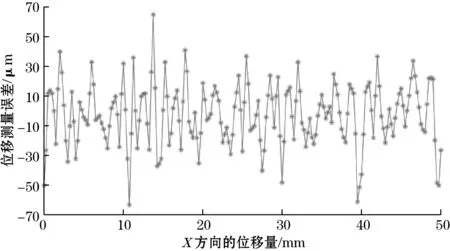
图10 位移测量的误差曲线图

4 结论

本文提出PCB基板上布置阵列的激励线圈和特定形状的感应线圈，通过调制感应面积和线圈参数的测量方法，阐述了测量方法的原理，并进行了仿真设计和实验验证，所得的结论如下：

(1)采用平面线圈阵列构建行波磁场，减小了绕线的不均匀性，并且线圈的宽度(y方向)距离越大，磁场的边缘效应对精度影响越小。

(2)将PCB工艺技术与时栅测量技术相结合，简化了定尺与动尺的加工工艺，提高了部件工艺的一致性。

(3)这种新结构设计虽然目前只能实现±68 μm的原始测量精度，但在不改变激励线圈和感应线圈空间极距的情况下，使得分辨力在信号源头上得以提高，为位移测量提供新的思路。进一步优化线圈结构，并对误差进行详细分析和应用误差修正技术，提高测量精度将是下一步的重点研究内容。