一种低信噪比下的LFM 脉冲信号起始频率校正方法*

陈万里，李 伟，柴远波

（黄河科技学院工学部，郑州 450063）

0 引言

由于线性调频信号（linear frequency modulated，LFM）具有较好的频移和时延分辨率，被广泛应用于雷达、声纳和通讯等系统中［1-3］。为了能够对LFM 信号实现检测和估计，研究人员首先提出采用时频分析方法对待处理数据进行变换处理分析，根据变换处理结果对其实现检测和估计，常用方法主要包括：如短时傅里叶变换［4-5］、小波变换［6］、Wigner 变换［7-9］等，但由于LFM 信号存在较强的时频耦合特性，在低信噪比下此类方法对LFM 信号检测与估计效果不太理想。为了解决时频分析方法受信噪比影响较大问题，研究人员进一步提出了时频分析与图像处理联合处理方法，但该类方法在实现过程需要求取LFM 信号时频分布或模糊度表面，并对求取结果进行图像识别，计算复杂度较高［10-13］，在实际应用中存在一定限制。

为了进一步克服上述方法实现LFM 信号检测与估计中存在信噪比影响问题，研究人员再次提出了一种新的LFM 信号检测与估计方法——分数阶傅里叶变换（The Fractional Fourier Transform，FRFT）方法，该方法在时频分析中通过增加相移因子，将原有傅里叶变换（The Fractional Transform，FFT）中直线分布变换为点分布，实现LFM 信号能量聚集［14-17］，降低了LFM 信号检测与估计对最低信噪比需求。由于FRFT 方法在实现LFM 信号能量聚集中需要对相移因子进行调节，存在一定计算复杂度，对此，陈艳丽［18］等人提出了一种简明分数阶傅里叶变换（The Concise Fractional Fourier Transform，CFRFT）方法，进一步扩展了FRFT 方法的可实现性。

但实际应用发现采用分数阶傅里叶变换对LFM 脉冲信号参数估计中，存在起始频率估计准确度受脉冲起始点影响问题。针对该问题，依据分数阶傅里叶变换中聚集的信号能量峰固有特性，提出一种适用于低信噪比条件下的LFM 脉冲信号起始频率校正方法。该方法首先通过FRFT 变换和chirp 相乘对数据进行变换处理，消除LFM 脉冲信号中调频斜率；然后对变换后结果进行滑动、累积处理，得到一组能量峰数据；最后通过搜索该组能量峰拐点实现对LFM 脉冲信号起始点检测，并利用检测起始点对LFM 脉冲信号起始频率实现校正。数值仿真结果表明，本文方法在事先无法获取处理数据中LFM 脉冲信号起始点情况时，可有效校正分数阶傅里叶变换对LFM 脉冲信号起始频率估计存在的偏差。

1 CFRFT 方法

1.1 基本原理

其中，k 为LFM 信号调频斜率，α、N 和f ' 分别为CFRFT 处理所用旋转角度、点数和不同角度下对应频率。

此时，CFRFT 等同于FFT。

由此，可引入一个中间变量，将式（1）可变为FFT 形式。

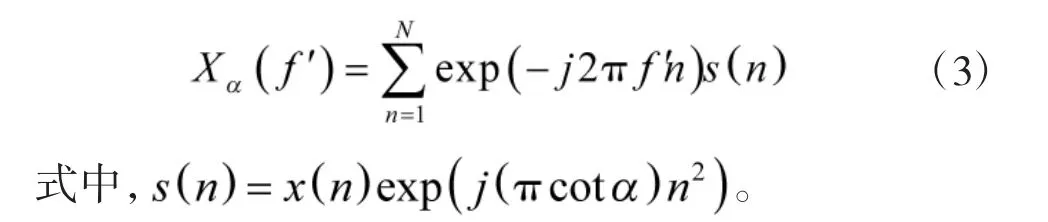
由处理过程可知，在坐标系（n，f）下，在时间坐标轴n 一定时，将对频率坐标轴f 按不同角度进行旋转，可得到不同旋转角度α 下的时频分析结果，在某一角度下实现能量聚集，进而实现对LFM 信号检测与估计。图1 为旋转角度为α 的CFRFT 示意图。

图1 旋转角度α 下，CFRFT 示意图

1.2 参数估计

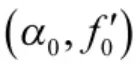
1.3 数值仿真

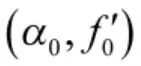
表1 数值仿真参数

图3 为SNR=10 dB，采用FFT 和CFRFT 处理所得结果；图5 为SNR=-10 dB，采用FFT 和CFRFT处理所得结果。两次数据处理中LFM 脉冲信号起始点与数据起始点一致，每一次处理数据x（n）长度为N=50 k。

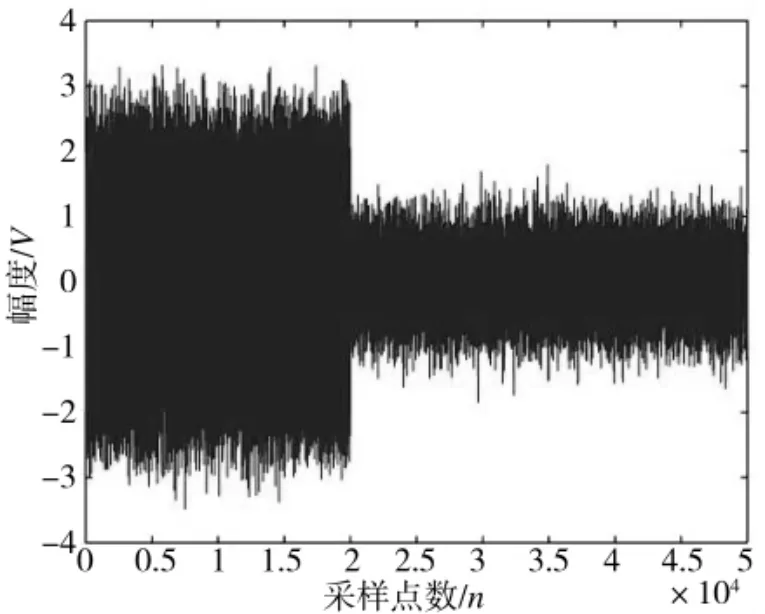
图2 时域图（SNR=10 dB）

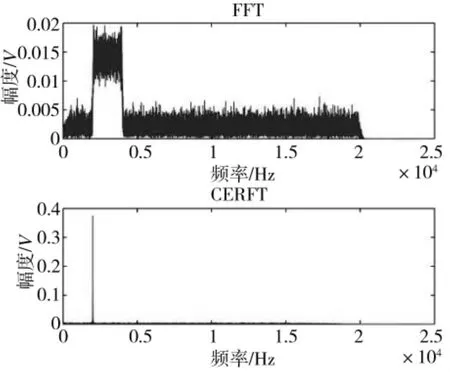
图3 频域与分数域变换图（SNR=10 dB）

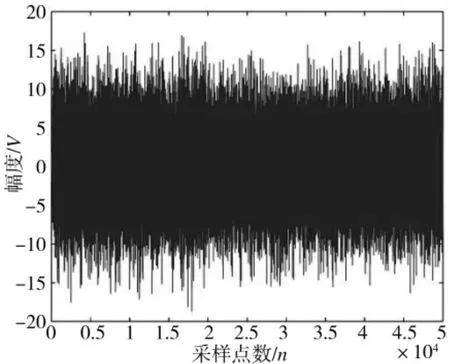
图4 时域图（SNR=-10 dB）

图5 频域与分数域变换图（SNR=-10 dB）

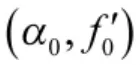
1.4 问题分析

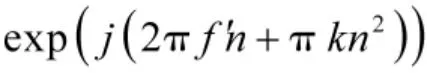
此时，采用式（3）对s（n）进行CFRFT 处理，LFM脉冲信号在f'轴上投影点与其真实起始频率存在一定偏差。为了直观说明CFRFT 处理过程中LFM脉冲信号起始点与x（n）起始点不一致所致时，所得LFM 信号起始频率估计值存在一定偏差，进行如下数值仿真，仿真条件为：

表2 数值仿真参数

图6 和图7 分别为N0=5 000 和N0=10 000 时所得变换结果。

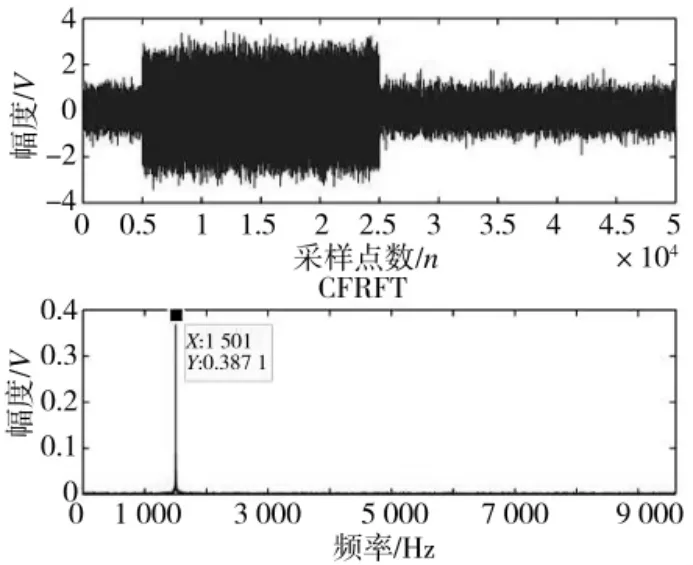
图6 时域与分数域变换图（N0=5 000）

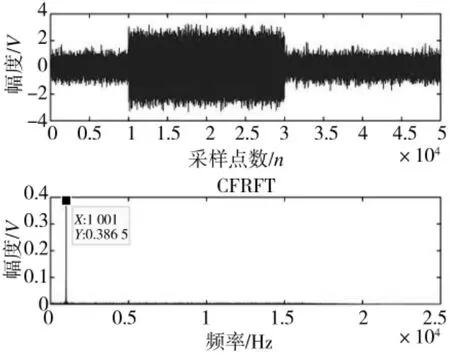
图7 时域与分数域变换图（N0=10 000）

由图6 和图7 处理结果可知，当LFM 脉冲信号起始点不等于处理数据起始点时，采用CFRFT 处理对LFM 脉冲信号进行检测和参数估计时，估计所得起始频率值存在一定偏差。当N0=5 000 时，CFRFT处理所得起始频率值为1 500 Hz；当N0=10 000 时，CFRFT 处理所得起始频率值为1 000 Hz；两者与起始频率真实值2 000 Hz 存在一定偏差。

2 本文方法

2.1 问题解析

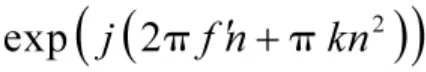
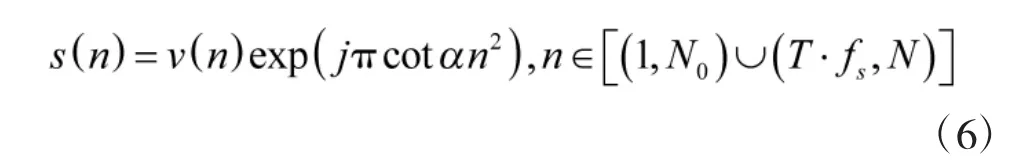
式中，v（n）为背景噪声数据。

2.2 实现过程

针对该问题，本文依据分数阶傅里叶变换中聚集的信号能量峰与处理数据包含脉冲信号长度关系，本文采用如下步骤实现对LFM 脉冲信号起始位置与处理数据起始位置不一致时，LFM 信号起始频率偏差问题。

步骤1 通过CFRFT 变换和chirp 相乘对数据x（n）进行变换处理，消除LFM 脉冲信号中调频斜率，形成式（3）中s（n）。

步骤2 按图8 和式（7）对s（n）进行第m 次滑动FT 处理，得到第m 次滑动处理结果Y（m，w）。

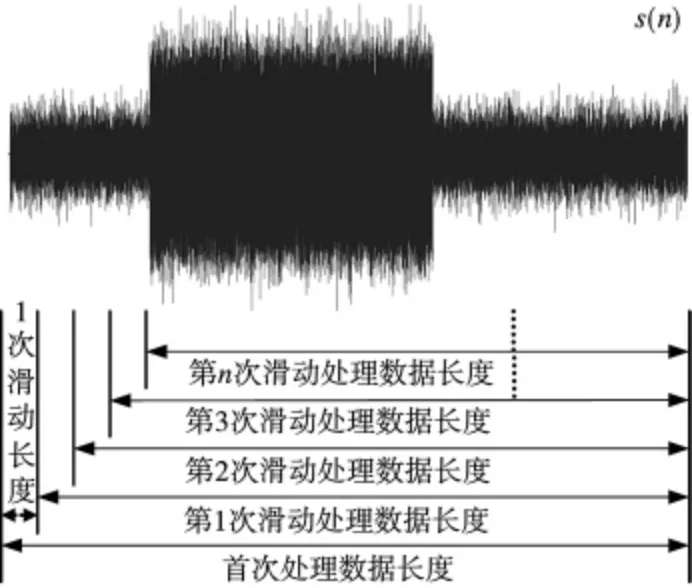
图8 本文方法滑动处理数据示意图

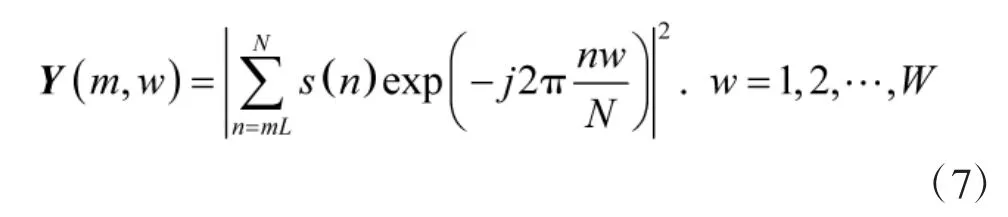
式中，W 为FT 变换频率点数，L 为一次滑动数据长度。

步骤3 按式（8）对第m 次滑动处理结果Y（m，w）进行峰值搜索，提取每次处理数据峰值处能量值，得到一组信号能量峰P（m）。

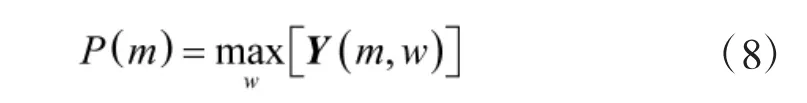
步骤4 m=m+1，更新滑动数据长度，重复执行步骤2 和步骤3，直到m 等于预设定滑动处理次数M。

步骤5 通过搜索P（m），m=0，1，…，M 的变化拐点，实现对LFM 脉冲信号在处理数据起始点检测，并按式（9）对LFM 脉冲信号起始频率实现校正。

2.3 数值仿真分析

为了进一步验证本文方法，可在事先无法获取处理数据中LFM 脉冲信号起始点情况时，可有效校正CFRFT 处理所得LFM 脉冲信号起始频率存在的偏差，进行如下数值仿真。仿真条件为：

表3 数值仿真参数

图9 和图10 分别为N0=5 000 和N0=10 000 时，通过本文方法所得能量峰变化图，数据处理中L=1。

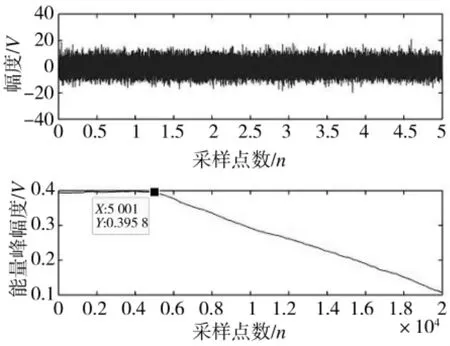
图9 能量峰变化图（N0=5 000）

图10 能量峰变化图（N0=10 000）

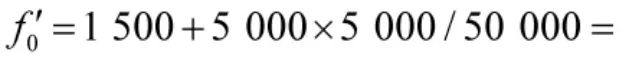
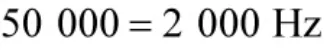
3 结论

针对分数阶傅里叶变换实现LFM 脉冲信号参数估计准确度与信号起始点位置关系问题，本文首先分析了CFRFT 处理实现过程、参数估计原理，然后对CFRFT 处理可在低信噪比下实现LFM 脉冲信号检测与估计进行了数值仿真验证，并对其存在的问题进行了分析说明；最后对于CFRFT 处理存在起始频率估计问题，提出了一种校正CFRFT 处理所得LFM 脉冲信号起始频率方法。数值仿真进一步验证了该方法可在无法事先获取处理数据中LFM 脉冲信号起始点情况时，可有效校正CFRFT 处理所得LFM脉冲信号起始频率值存在的偏差。为低信噪比下的准确估计LFM 脉冲信号起始频率提供了一种路径。