基于非凸范数最小化图像去噪算法*

徐 可，王洪雁

（1.周口师范学院网络工程学院，河南 周口 466000；2.大连大学信息工程学院，辽宁 大连 116622）

0 引言

采集、传输以及处理过程中，数字图像无可避免被噪声所干扰，导致部分细节丢失，从而使得图像质量显著下降［1-2］。为提升噪声污染图像质量，可精确恢复原始图像并尽可能保留边缘及纹理信息的图像去噪相关算法被提出。然而，由于图像去噪模型的欠定性，所得优化问题的求解较为困难，因此，基于图像相关先验信息获得去噪优化问题的有效求解进而实现高效去噪已成为图像去噪领域的研究热点［3-4］。

根据图像先验信息的空域分布，图像降噪算法可分为如下两类：局部先验信息方法以及非局域自相似（NSS）先验信息方法。局部先验信息方法主要包括基于小波收缩方法（WS）［5］，全变分方法（TV）［6］和基于退火算法的改进图像去噪方法（PID）［7］。上述算法仅利用图像局部先验信息，忽略非局域图像空域之间相似性，从而使得去噪算法性能有限。非局域图像空域相似性是指：基于给定图像非局域相似块之间线性相关的物理事实，搜索相似于给定区域的图像块，实践表明NSS 已成为图像恢复任务中非常有效的先验信息［8］。由此，基于加权平均相似图像块以提升去噪性能的非局域均值去噪（NLM）方法被提出，然而当图像信噪比较低时，由于相似区域噪声成分较多，从而使得所得去噪图像模糊［9］。基于此，三维块匹配（BM3D）算法被提出，其将多个相似二维图像块重构为三维数据以实现联合去噪从而提升去噪性能，然而因其相似图像块查找及三维数据联合去噪计算复杂度较高，因而限制了此算法的实际应用［10］。针对此问题，组稀疏的非局域集中稀疏表示（NCSR）方法被提出，然而此算法所得去噪图像具有较强伪影及关键纹理细节模糊等问题［11-12］。针对上述问题，相关研究表明：矢量化非局域相似图像块并聚合为矩阵，则此矩阵由于列矢量之间相关性而呈现低秩特性［13］，因此，可基于其低秩空域先验知识改善去噪性能。由此，基于核范数逼近秩函数以构造低秩去噪模型的核范数最小化（NNM）方法被提出，然而由于此算法平等对待各奇异值，而忽略各奇异值表征先验信息重要性的不同，因而去噪性能改善有限［14］。基于此，加权核范数逼近秩函数以体现各奇异值不同重要性的加权核范数最小化（WNNM）方法被提出，然而，基于核范数逼近秩函数将过惩罚较大奇异值，从而使得所得去噪优化问题无法获取最优解［15］。

针对上述图像去噪性能改善有限的问题，基于可无偏逼近秩函数的伽马范数［16］，基于伽马范数最小化的图像去噪方法被提出。所提方法基于结构相似性指数（SSIM）搜寻相似区域以提升相似块搜索精确性，而后基于伽马范数无偏逼近秩函数的特性构建低秩去噪模型，最后基于凸优化理论求解低秩去噪优化问题。与PID，NLM，BM3D 和NNM 等主流去噪算法相比，实验结果表明，所提方法可有效滤除高斯噪声，并尽可能保持原始图像细节。

1 低秩去噪概述

将上述操作作用于各重叠块，并重组各图像块即可重构原始图像。然而，需要注意的是，作为有偏估计子的核范数，其逼近秩函数可过惩罚较大奇异值，从而导致上述最优化问题仅可获得次优解，进而使得去噪性能提升有限［20］。基于此，本文利用伽马范数替换核范数以无偏逼近秩函数，进而提升低秩去噪模型性能。

2 基于伽马范数最小化的图像去噪算法

基于欧氏距离的传统非局域相似块搜寻方法忽略空域间相似性，从而使得非局域相似块搜寻性能较差［21］。为提升相似块搜寻性能，本文提出基于SSIM 的自适应相似图像块搜索方法。SSIM 是一种综合的图像相似性评价指标［22］，其考虑图像间亮度，对比度和结构3 个不同特性，可较好评价两幅图像的相似程度。给定两幅图像x 和y，SSIM 定义如式（5）所示：

自适应相似块搜寻思想可表述如下：给定图像块yi及图像数据集，计算yi与图像数据集中分割所得图像块的SSIM，其值越大表明二者相似度越高，基于此，搜寻相似度最高的m 个图像块，相似块数需基于噪声特征自适应确定。而后矢量化相似块并基于相似度降序自左至右排列以构建相似块矩阵Yi。

基于以上所述，所提相似块搜寻方法可有效利用非局域自相似先验知识以改善相似块搜寻精度。基于所得矩阵Yi，所提伽马范数最小化的低秩去噪模型可表述如下。

表1 所提算法去噪流程

3 仿真结果及分析

为验证所提算法去噪性能，实验选取标准图像库中6 幅图像进行测试，分别为256×256 Monarch、720×576 Boats、512×512 Lena、512×512 Pepper、256×256 House 和720×576 Barbara，如图1 所示。采用PID［7］，NLM［9］，BM3D［10］和NNM［14］作为对比算法。仿真软硬件环境为：Intel Core i7-7700，处理器主频3.60 GHz，内存8 GB，64 位Windows 10，Matlab R2014a。

本节基于文献［26］所提峰值信噪比（PSNR）定量评价去噪效果。给定图像x 和y，PSNR 定义如式（17）所示：

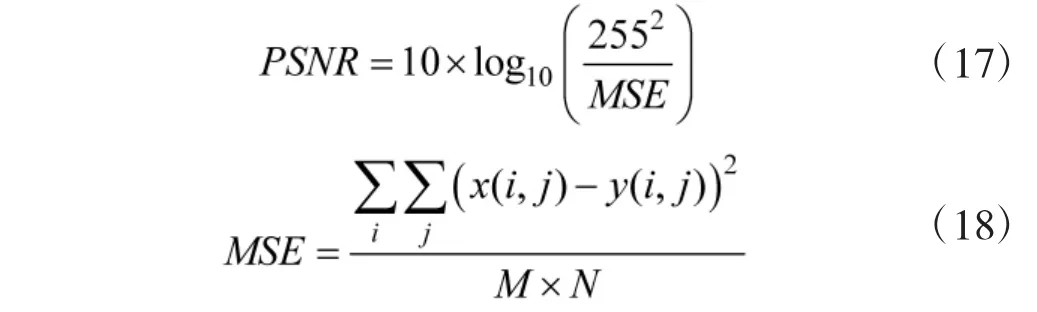
其中，MSE 表示均方误差，M×N 为两幅图像尺寸。

图1 六幅测试图像

对6 幅测试图像分别添加零均值高斯白噪声以生成噪声图像。由于篇幅限制，本文只显示3 个噪声等级去噪结果。其中，对于噪声方差σn=10，σn=50 和σn=100，不同算法去噪结果如下页表2 所示，最高PSNR 用粗体表示。由表2 可知，NLM 去噪性能不明显，而所提算法几乎每种情况皆可获得较高的PSNR。相比PID，NLM，BM3D 和NNM 算法，所提算法PSNR 分别平均提高0.32 dB，2.76 dB，0.35 dB及1.99 dB，随着信噪比降低，PSNR 提升较为明显。此可归因为所提方法基于SSIM 块匹配以改善相似块搜寻精确度，且基于伽马范数改善秩函数近似度。基于以上所述，相较于对比算法，不同噪声特征条件下所提算法均可获得优良的去噪效果。

对于噪声方差σn=50 的House 图像，不同算法去噪结果分别如图2 所示。由图2 可知，基于NLM算法所得去噪图像模糊较大，此可归因于NLM 搜寻相似块具有大量噪声，且仅加权平均相似块以实现去噪；而NNM 算法基于低秩先验知识以消除模糊，然其平等对待各奇异值导致去噪结果关键纹理细节模糊；PID 算法基于空频联合处理以应对纹理细节丢失，细节模糊仍存在；BM3D 算法基于联合滤波以提升去噪性能，但去噪图像存在较强伪影。所提算法则采用基于SSIM 的相似图像块搜索方法，并利用伽马范数无偏逼近秩函数以应对上述问题。由图2（f）易知，本文方法所得去噪图像伪影较弱，且边缘及纹理等关键特征保持较好。综上所述，相较于对比算法，所提方法去噪性能提升明显，其不仅有效避免模糊及伪影，且可有效保持原始关键细节。

4 结论

针对传统去噪算法降噪性能较差的问题，本文提出基于无偏逼近秩函数的伽马范数最小化的去噪方法。首先将噪声图像重叠分块并采用基于SSIM的块匹配算法构造相似块矩阵，以应对传统方法相似块搜寻精度较低的问题；而后基于伽马范数构造低秩去噪模型，以避免传统秩逼近方法估计性能较差的缺点；最后基于凸优化理论求解所得优化问题并重组去噪块以获得最终去噪图像。相较于主流去噪算法，实验结果表明，所提方法可有效滤除高斯噪声，且尽可能保持原始图像细节。

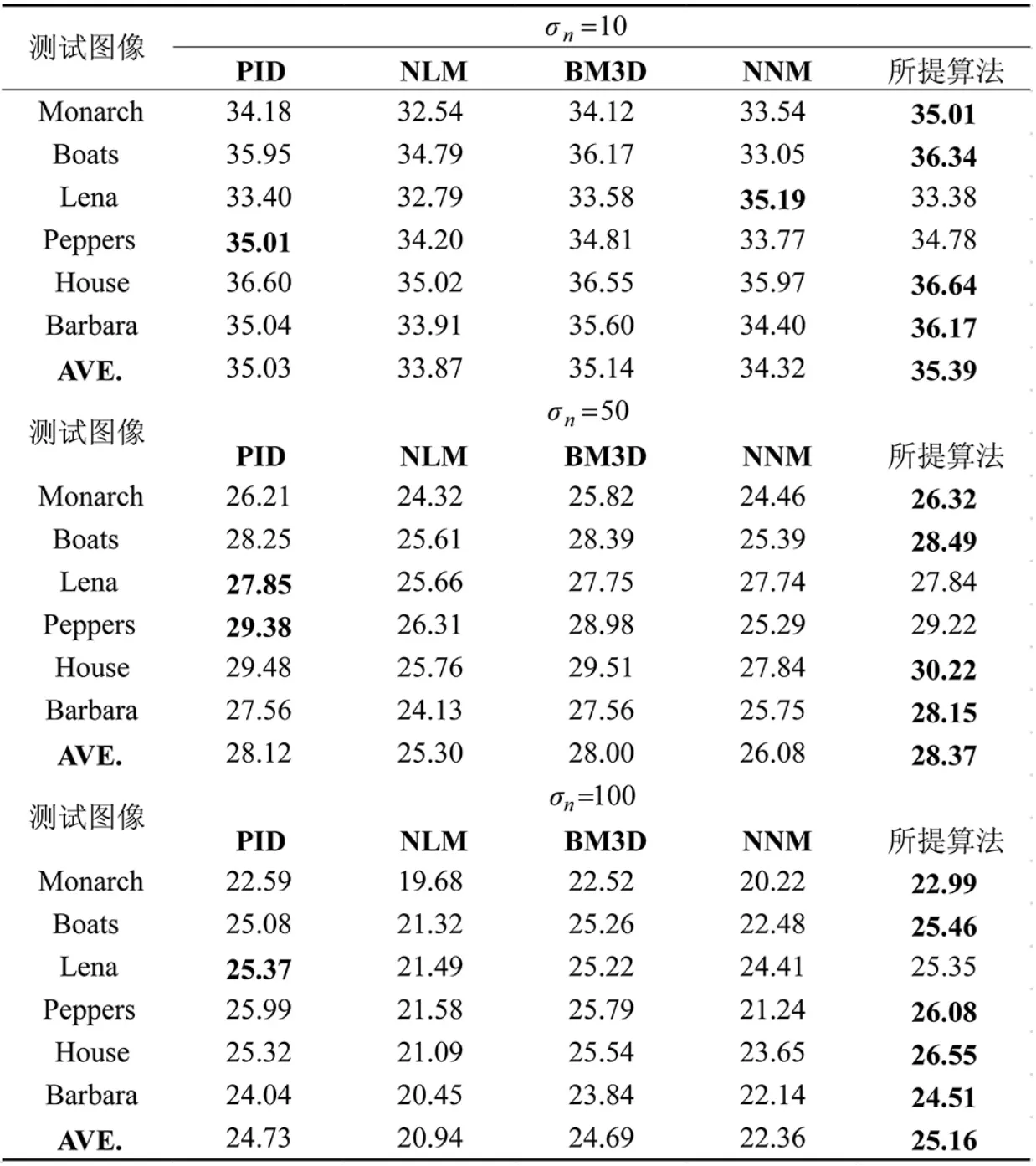
表2 不同去噪算法PSNR 对比

图2 不同算法对House 图像去噪结果（σn=50）