基于最小二乘正则相关性分析的颅骨身份识别

周明全，杨 稳，林芃樾，耿国华，刘晓宁，李 康

（1.西北大学信息科学与技术学院，陕西西安710127；2.北京师范大学信息科学与技术学院，北京100875）

1 引 言

颅骨身份识别是法医学中一个重要的研究课题。在很多法医学案例中，技术人员只能获取到受害人的颅骨，并且没有其他证据线索，这种情况下无法使用传统的身份识别技术，颅骨识别［1］便成为受害者身份认证的重要技术手段之一。随着CT、3D扫描等数字化技术的发展，三维颅面采集变得更加容易，计算机辅助颅骨识别成为研究热点，内容涉及法医学、信息学、人类学和计算机图形学等多个领域。

目前，颅骨识别研究主要集中在颅像重合［2］和颅面复原［3］两方面。颅像重合是将未知身源颅骨的2D投影与失踪人2D照片相叠加，根据其相关特征找到一个合适的匹配，从而获取到颅骨人脸叠加像，即可判断颅骨和人脸照片是否属于同一人。颅面复原［4］是通过分析颅骨和面皮之间的内在关系，复原出未知颅骨面貌的技术。当前主流的颅面复原方法采用统计学习技术，如统计形状模型［5］和统计回归模型［6］等。

颅像重合［7-11］和颅面复原［12-13］都需要利用形态学知识准确提取颅骨和面皮之间的内在关系，存在不确定性较高和识别能力较低等问题。随着基于图像的3D人脸建模［14］和3D数据采集技术［15］的发展，使用3D颅骨和3D面皮之间的相关性识别颅骨逐渐成为研究热点问题。Duan［16］等人首次提出通过分析颅骨和面皮之间的形态相关度来识别未知颅骨，并使用典型关联分析［17］提取映射后两组相关性最大的主成分向量，用于匹配颅骨和面皮。但由于颅骨与面皮之间关系复杂，该方法的识别率有待提高。

本文提出了一种基于最小二乘正则相关性分析（Least-Squares Canonical Dependency Anal⁃ysis，LSCDA）的颅骨识别方法。该方法通过构建颅骨和面皮的相关性分析模型，计算未知颅骨和面皮库中每张面皮的匹配程度，得到识别结果。与颅像重合和颅面复原不同，该方法无需准确提取颅骨和面皮之间内在的复杂关系，仅测量它们之间的相关性即可确定颅骨身份，降低了颅骨识别问题的复杂性，提高了识别率。

2 数据获取与预处理

本研究使用了255套颅面数据，这些数据来源于西北大学可视化技术研究所，女性年龄在19～75岁，男性年龄在21～67岁。颅面CT数据由陕西中医药大学附属医院使用西门子多排探测器螺旋CT机采集，每个图像以DICOM格式存储，大小约为512×512×250。原始CT切片图像在去噪后，使用Sobel算子提取颅骨和面皮轮廓，采用Marching Cube算法［17］进行重建，得到颅骨和面皮的三维模型。颅骨和面皮分别表示为大约包含220 000和150 000个顶点的三角形网格。另外，每套颅面还记录了年龄、性别和BMI等属性。

为了消除因位置、姿态和尺度等因素造成的数据不一致，所有样本都被转换在统一的法兰克福坐标系下。法兰克福坐标系是由左右双侧耳门上点、左眼眶下边缘点和眉间点4个颅骨特征点确定的，分别用Lp，Rp，Mp和Vp表示。法兰克福平面由Lp，Rp和Mp3点确定［18］。如图1所示：以Lp Rp为法向量且过点Vp的平面与直线Lp Rp的交点记为法兰克福平面的原点O′；Lp，Rp以及Mp3点所构成的平面为坐标系中的XO′Y平面，左耳门上点Lp到右耳门上点Rp的方向为X轴方向；过原点O′且与XO′Y平面垂直向上的方向记为Z轴；同时垂直于X轴、Z轴的直线记为坐标系的Y轴，Y轴的正方向由右手法则确定。

图1 归一化坐标Fig.1 Normalized coordinates

统一坐标系后，再进行尺度归一化。设定所有颅骨模型的Lp到Rp的距离为单位1，则对颅骨每一个顶点（x，y，z）进行尺度变换为（x/|LpRp|，y/|LpRp|，z/|LpRp|）。

由于面部特征信息主要集中于前半部分［19］，为了消除不相关数据的影响和减少算法耗时，对颅面样本进行分割，只保留与识别有直接关系的前半部分，分割后的颅骨和面皮分别为包含约160 000和80 000个顶点的三角形网格。为了建立相同的点对应关系，选取一组分割后的颅骨和面皮作为参考模板，如图2所示。其余所有颅骨模型和面皮模型通过非刚性配准方法［20］自动配准到参考模型中。

图2 颅骨和面皮参考模型Fig.2 Skull and skin reference models

3 构建统计形状模型

在进行LSCDA分析前，需要分别为颅骨和面皮建立统计形状模型。统计形状模型［21］是一个参数化的可变形模板，每个颅面都有一个参数化的表示，即每个颅面对应着参数空间中的一个点。主成分分析（Principal Components Analysis，PCA）是建立颅面统计形状模型的有力工具。PCA能够反映训练样本数据集真实分布的一组正交轴，这组正交轴原点设在数据集的中心，表示训练数据中具有最大方差的一组方向，数据能够以最小误差重构，从而达到降维的效果。

通过连接所有顶点的坐标，颅骨和面皮可以分别表示为一个高维度的向量。因此，得到一个颅骨的训练数据集和一个面皮的训练数据集其中N表示训练样本个数，m和n分别为颅骨和面皮的顶点数，每个坐标索引标记训练集上的对应点。假定P1，P2，...，Pp是均值归一化颅骨协方差矩阵的单位正交特征向量是样本颅骨向量的均值。PCA变换可以将每一个颅骨向量Si通过变换投影到以均值为原点，以这些主方向为坐标轴的坐标系中。那么，颅骨统计形状模型可以表示为：

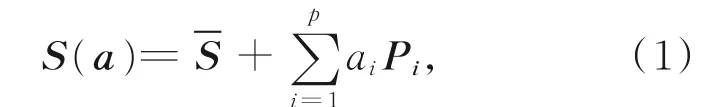
其中：a=(a1，a2，...，ap)Τ是组合参数，ai满足高斯分布，在模型中只要给定组合参数a即可产生颅骨参数模型S(a)。

所有颅骨数据和面皮数据均进行了非刚性配准操作，具有相同的点对应关系，可以通过PCA变换来确定形状模型参数。对于每一个颅骨向量Si，变换为：

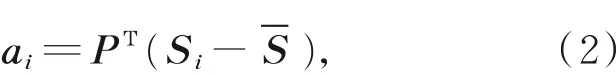
其中：P=[P1，P2，...，Pp]，ai∈Rp称为颅骨向量Si的主成分向量。类似地，可通过相同的处理过程来构建面皮统计形状模型：

因此，通过构建统计形状模型，将颅骨和面皮数据分别投影到其低维形状参数空间ap和bq中。

4 颅骨和面皮的主相关信息提取

通过构建统计形状模型，每个颅骨可以表示为p维特征向量，每个面皮表示为q维特征向量。LSCDA旨在通过平方损失互信息［22］（Squaredloss Mutual Information，SMI）找到ap和bq之间的统计相关关系，它可以在线性投影下捕获两个变量的主相关信息。

因此，用LSCDA找到ap和bq的低维子空间，投影的相关性通过线性降维达到最大值，即有：

其中U和V是转换矩阵。

其中p和q分别是u和v的投影维数，Ip是p维单位矩阵，Iq是q维单位矩阵。

由此可知，寻找转换矩阵U和V使得u和v之间的相关关系最大化。这里通过SMI来测量其相关性：

其中：pu，v(u，v)是联合概率分布密度，pu(u)和pv(v)分别是u和v的边缘概率分布密度。

然而，pu，v(u，v)，pu(u)和pv(v)通常是未知的，不能直接最大化SMI。因此，本文采用最小二乘互信息（Least-Squares Mutual Information，LSMI）方法直接估计密度比，而不用估计每个密度，即有：

密度比函数g∗(u，v)由线性组合建模表示为g(u，v)，具体如下：

其中α=(α1，α2，...，αb)Τ是从样本中学习的参数，φ(u，v)=(φ1(u，v)，φ2(u，v)，...，φb(u，v))Τ是一个基函数，并且对于所有的u和v，φ(u，v)≥0b，0b是一个b维零向量。

参数α是通过最小化平方误差δ来估计的，即：

这里，令：

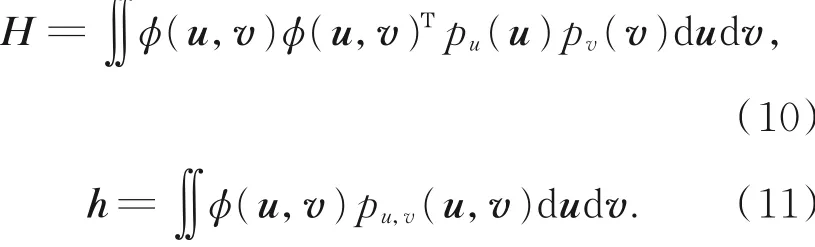
于是有：

近似估计H和h的值如下：

将问题转换为：

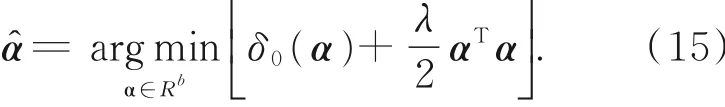
通过计算上述目标函数的导数并将它设为零，可以得到：

其中Ib是b阶单位矩阵。

那么SMI的近似值表示如下：

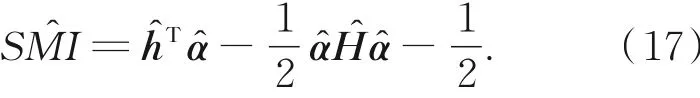
综上所述，颅骨和面皮之间的主相关关系提取算法过程如下：

首先，最合适的变换矩阵U和V是以迭代的方式确定的，具体步骤如下：

Step1：根据式（4）初始化U和V；

Step2：根据式（16）对参数α进行优化；

Step3：采用序列二次规划技术来更新U和V，重复此过程直至收敛。

然后，通过线性投影将颅骨形状参数转换成LSCDA空间参数，即：

同理，通过线性投影将面皮形状参数转换为LSCDA空间参数，即：

最后，计算库中的未知颅骨与每张面皮的匹配分数，匹配得分最高的面皮就是识别结果。定义颅骨和面皮之间的匹配程度如下：

其中<⋅，⋅>表示内积。

5 基于LSCDA的颅骨识别方法

未知颅骨与面皮之间的识别将分别从整体和区域两个方面进行。首先，构建整体相关性分析模型，从全局来分析颅骨和面皮之间的关系；其次，由于颅面形态非常复杂，不同颅骨和面皮不同区域的相关度不同。例如，前额区域的相关性较强，因为该区域的软组织厚度较薄；而鼻子、眼睛和嘴巴等区域的相关性则较弱，因为这些区域的结构复杂。强关联区域具有较高的识别能力。然而，整体相关性分析模型只反映了全局意义上颅骨和面皮之间的相关性，并没有充分利用它们的特性信息。为了更加可靠地测量颅骨与面皮之间的相关性，提高识别能力，提出了一种基于区域的局部化识别方法。识别流程如图3所示。

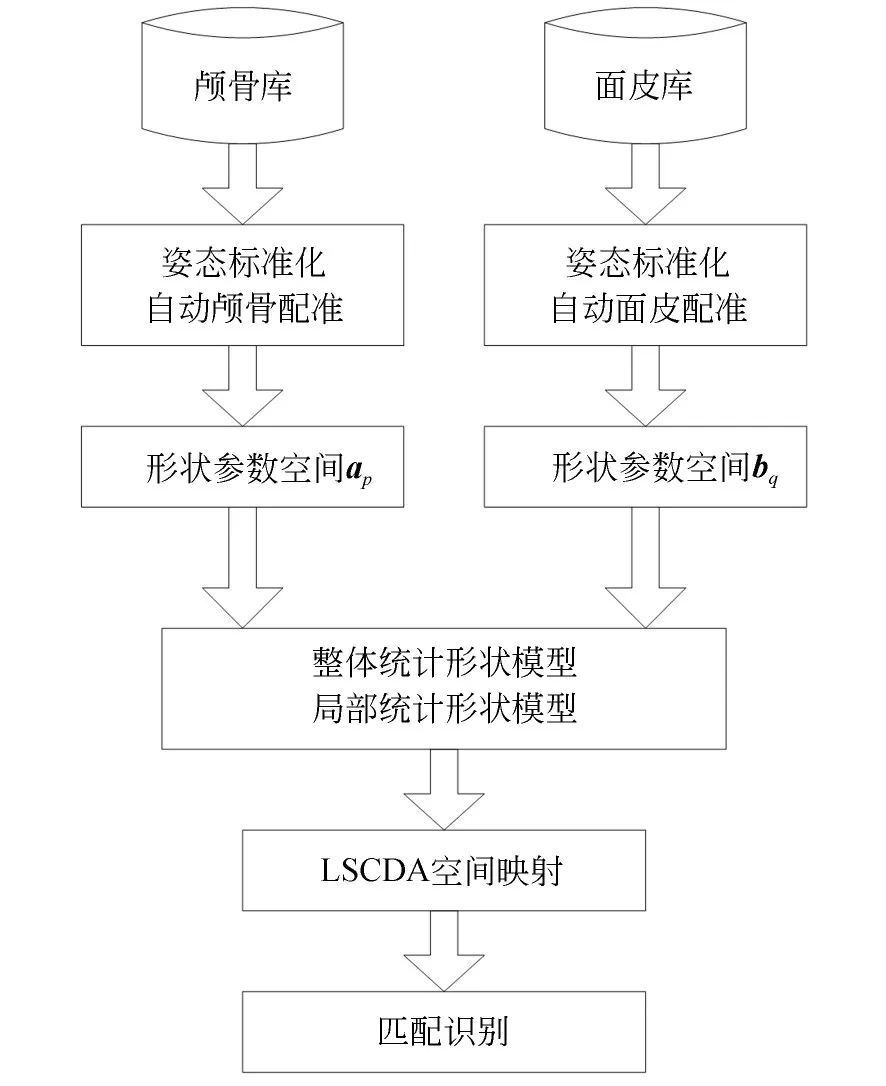
图3 基于区域的颅骨识别流程Fig.3 Flow chart of skull recognition based on regional fusion method

5.1 基于LSCDA的整体颅骨识别

基于LSCDA整体颅骨识别的目的是从三维面皮库中找到一个与未知颅骨最可能匹配的面皮。因此，需要计算未知颅骨与每个3D面皮之间的匹配分数。整体颅骨识别的框架如图4所示，识别过程包括两个阶段：训练阶段和识别阶段。其中，S表示颅骨训练集，F表示面皮训练集，u和v分别表示LSCDA提取后的子空间向量。

训练阶段，建立相关性分析模型的步骤如下：

Step1：使用所有训练数据构建颅骨和面皮的统计形状模型，如式（1）和式（3）所述；

Step2：根据式（2）将所有训练数据投影到形状参数空间中；

Step3：针对训练颅骨和面皮的形状参数特征执行LSCDA，并获得两个映射向量u和v。

识别阶段，使用相关性分析模型识别未知颅骨，步骤如下：

Step1：通过上述的统计形状模型将未知颅骨和面皮库中的面皮分别投影到形状参数空间中；

Step2：根据式（4），将它们的形状参数特征投影到LSCDA子空间中。

图4 整体颅骨识别框架Fig.4 Flow chart of skull recognition based on holistic approach

Step3：根据式（20）计算未知颅骨与面皮库中每个面皮之间的匹配分数，具有最高匹配分数的面皮即为识别结果。

5.2 基于LSCDA的区域颅骨识别

如图5所示，将颅骨和面皮分成几个相应的生理特征区域，即前额、眼睛、鼻子、嘴巴和轮廓。训练集之间的对应关系已经建立，只需要手动分割一个样本，其他样本可以通过点对应关系实现自动分割。基于LSCDA的区域颅骨识别框架与上述整体颅骨识别框架大致相同，采用该框架分别为5个区域构建相关性分析模型。在识别阶段，可以单区域相关性分析进行未知颅骨的识别；还可以将5个相关性分析模型进行融合，进一步提高未知颅骨的识别率。

对于一个颅骨和面皮匹配对，可以使用5个相关性分析模型获得5个区域匹配分数，最终匹配分数通过加权和计算，如式（21）所示：

图5 颅骨和面皮的各个区域Fig.5 Various areas of skull and face

其中：rp，rf，re，rm和rn分别代表轮廓、前额、眼睛、嘴巴和鼻子的区域匹配分数；wp，wf，we，wm和wn分别表示各个区域相对应的权值。

如何选择式（21）中每个区域的权值对颅骨识别起到决定性的作用。由于颅骨识别依赖的是颅骨与面皮之间的相关性，因此应该将高权重分配给高相关的区域，如轮廓和前额。相比之下，颅骨和面皮之间的关系在鼻子，眼睛和嘴巴等相关性较弱的区域是不确定的，但是这些区域可以为人脸识别提供更多的判别信息。

6 实验结果与分析

本文使用第2节介绍的三维颅面数据进行实验，并采用五折交叉验证来评估本文方法的有效性。将数据集分为5组，每组包括51个三维颅骨和面皮对。对于每一次折叠，选择其中一组51个三维颅骨面皮对作为测试集，剩余的204个颅骨和面皮构成训练集，也就是说，在5次折叠中共有255个三维颅骨作为测试集。对于每一个测试颅骨，所有的255个面皮构成查询集。整个实验的正确识别率是5次验证的平均值。

6.1 整体相关性分析

在PCA中大特征值对应的主成分向量表示训练数据集的变化模式，而小特征值对应的主成分向量则表示噪声方向。在这里，本文首先讨论了统计形状模型的方差贡献率对颅骨识别率的影响。由式（1）所述，模式数量由从累积特征值计算的方差贡献率确定，当方差贡献率从95%变化到99.5%时，整体模型的正确识别率如表1所示。从表1中可以看出，随着方差贡献率的增加，识别率逐渐提高；在方差贡献率达到99%时，识别率达到最高；当方差贡献率再继续增加时，识别率反而会下降。

表1 不同方差贡献率的整体模型的正确识别率Tab.1 Correct recognition rates of overall model with different variance contribution rates

对于每次折叠，构建一个整体统计形状模型，当方差贡献率为99%时，颅骨和面皮数据投影到低维形状参数空间中，分别表示为548和356维特征向量。基于LSCDA的全局颅骨识别通过提取基向量，正确识别率达85.2%，由此表明基于颅骨和面皮相关性分析的颅骨识别方法是有效的。进一步分析识别错误发现，误匹配面皮与真实面皮之间的全局形态相似性较高，从而导致了误匹配。图6为两个面皮之间的几何距离比较，从误差分析图可以看出，相似人脸与真实人脸大部分区域的几何距离都很小。由于两个面皮的全局形态相似性程度高，因此具有相似的形状模型参数，使得整体模型产生错误匹配。

图6 相似人脸之间距离的比较Fig.6 Comparison of distances between similar faces

6.2 区域相关性分析

为了验证区域相关性分析模型，分别为每个区域构建区域统计形状模型，然后进行区域LSCDA映射，完成匹配。当方差贡献率为99%时，与基于整体相关性分析的LSCDA颅骨识别相对比，可以得到区域相关性分析的颅骨识别率，如表2所示。

表2 颅骨单一区域识别率Tab.2 Recognition rate of skull single area（%）

通过对比发现，轮廓、前额和整体模型的识别率相当，这是因为轮廓和前额在整体模型相关性测量中起着决定性作用。鼻子主要由软骨组成，嘴唇与口腔区域的牙齿分离，因此与嘴巴、鼻子区域相比，眼睛的形态对眼眶骨形状的依赖性更强，从而识别率也较高。

表3 为区域相关性分析的正确识别率，图7显示了不同方差贡献率的局部模型识别率的变化趋势。

表3 不同方差贡献率的局部模型的正确识别率Tab.3 Correct recognition rates of local models with dif⁃ferent variance contribution rates （%）

图7 不同方差贡献率的局部模型识别率变化趋势Fig.7 Variation of local model recognition rate with vari⁃ance contribution rate

从表3和图7可以看出，当方差贡献率增加时，前额和轮廓的识别率变化很快，尤其是前额区域，这是因为较多地舍弃了变化模式中包含的一些特性信息。由图7可知，当轮廓、前额、眼睛、鼻子和嘴巴区域的方差贡献率分别为99%，99.5%，98%，97%和98%时，这些区域的识别率最高。在使用基于区域相关性分析进行颅骨识别时，对不同区域选择不同的方差贡献率来构建局部统计形状模型，可以提高颅骨识别的准确率。

此外，通过实验发现，各个区域权重经过融合之后将达到最优的识别准确率。区域权重如下：

其中i=p，f，e，n，m，对应轮廓、前额、眼睛、鼻子和嘴，ri表示对应区域模型的正确识别率。因此，融合权重可以根据式（22）在实际情况中具体设定。

表4 区域融合权重Tab.4 Regional fusion weights

表4 显示了本实验中选择不同方差贡献率进行颅骨识别时各区域的融合权重。基于得到的融合权重，通过区域融合识别颅骨。在测试阶段，第一次验证时，51个测试颅骨中出现错误识别个数为2，识别准确率为96.0%；第二次验证时，51个测试颅骨中出现错误识别个数为1，识别准确率为98.0%；第三次验证时，51个测试颅骨中出现错误识别个数为3，识别准确率为94.1%；第四次验证时，51个测试颅骨中出现错误识别个数为2，识别准确率为96.0%；第五次验证时，51个测试颅骨中出现错误识别个数为4，识别准确率为92.1%。因此，通过融合5个区域建立的相关性分析模型得到，识别准确率为（96.0%+98.0%+94.1%+96.0%+92.1%）/5=95.2%。

为了验证本文方法的优越性，我们分别与文献［16］和文献［23］中的方法进行对比。3种方法的对比结果如表5所示。

表5 不同方法识别准确率的对比Tab.5 Comparison of recognition accuracy of different methods

从表5可以看出，本文方法的识别准确率最高，文献［16］方法次之，文献［23］方法的识别准确率最低。文献［23］中使用嵌入式隐马尔可夫模型，虽然充分利用了颅骨的形状和整体结构信息，但是使用颅骨二维图像，丢失了颅骨的空间信息；而文献［16］和本文均使用颅骨三维模型，并且两者都是利用颅骨和面皮之间的形态关系进行识别。文献［16］首次提出通过分析颅骨和面皮之间的形态相关度来识别未知颅骨，并使用典型关联分析提取映射后两组相关性最大的主成分向量，用于匹配颅骨和面皮。与文献［16］相比，本文采用LSCDA方法分析颅骨和面皮的相关性，通过两个对变量投影的LSMI测量相关性，并通过线性变换使相关性达到最大。该方法不仅能通过线性投影提取两个变量的最相关信息，还可以消除无关信息，因此识别准确率更高。

7 结 论

本文提出了一种基于三维颅骨与三维人脸形态相关性度量的未知颅骨识别技术。使用三维颅骨数据作为探针，三维人脸数据作为匹配库，通过探针和匹配库之间的相关性度量，将未知颅骨与已配准的三维人脸进行匹配，从而实现颅骨身份识别。首先，构建颅骨和面皮的统计形状模型，将高维颅骨和面皮映射到低维形状参数空间；然后，基于LSCDA提取颅骨和面皮的主相关信息，构建整体相关性分析模型；最后，计算颅骨与面皮库中每个面皮之间的匹配分数，具有最高匹配分数的面皮即为正确的识别结果。为了提高匹配的准确性，将颅骨和面皮划分为5个生理特征区域，分别为前额、眼睛、鼻子、嘴巴和轮廓，建立5个区域的相关性分析模型，并通过区域融合进行颅骨识别。与颅像重合和颅面复原相比，本文方法不需要颅骨和面皮之间的精确关系，就可以实现未知颅骨身份的确定。本研究证明了颅骨和面皮之间确实存在着较为紧密的联系，为颅像重合和颅面复原的研究提供了理论支持。此外，在提取颅骨和面皮之间的关系方面，基于区域的策略要优于整体策略，这也为基于区域的颅面复原研究提供了参考。

随着基于图像的三维人脸建模技术和三维数据采集技术的发展，三维颅面模型获取变得越来越容易，扩展三维颅面数据集从而进一步提升本文方法的识别率，使它能够更为广泛地用于实际案例中，是下一步的研究重点。