基于侧重点聚类的数学表达式相似度计算方法
杨 芳,尹 曦,司建辉,刘宏媛,汪 雪
河北大学 网络空间安全与计算机学院,河北 保定 071002
数学表达式是科技文档中不可缺少的表现形式,对科技文档的检索有着重要的参考价值。随着科技文档数量的指数级增长和对科技文档检索要求的提高,对数学表达式的相似度计算也提出了更高的要求[1-2]。数学表达式具有丰富的语义和复杂的结构,目前对数学表达式相似度计算的方法主要从表达式的内容和结构匹配两个方面展开。
基于内容的相似度计算是较早提出的方法,MathDex[3]、ZHANG 等[4]、XU 等[5]均是根据数学表达式的内容为表达式分配权重,计算相似度。同时表达式的结构相似度计算也受到了重视,树形结构是常用的结构表示方法。文献[6-8]在树形结构的基础上利用关键词、关键字数目比例、运算符等信息构建索引得到查询表达式的相似表达式集合。ZHONG等[9]使用倒排索引和秩的动态剪枝算法来提高表达式匹配效率,实现更快的表达式子结构匹配。
数学表达式的内容与结构相结合的相似度计算方法也受到了广泛关注[10-11]。SHUNSUKE 等人[12]提出了一种基于散列的近似计算算法,采用Subtree Hash、Modular Trick、SIGURE Hash 三种哈希算法分别对应表达式的变量名称、功能结构和α-等价三种测度来计算表达式的相似度,在考虑到表达式结构的同时可以捕捉到数学表达式不同特征的语义相似性,该方法所用的计算时间较短,且对表达式中各个元素考虑周全,得到的相似度计算结果准确度较高。
侧重点是一个较为主观的概念且数学表达式数目庞大,很难人为地对其进行归纳,本文使用K-means++算法[14]对表达式的侧重点进行聚类归纳。K-means++聚类算法是K-means聚类算法[15]改进算法之一,该算法在计算机领域应用广泛,在算法模型的改进、文本分类等[16-17]方面都起到重要的作用。其原理简单,容易实现,收敛速度快,簇与簇之间区别明显,将K-means++聚类算法用于数学表达式相似度计算中,可以很好地将侧重点不同的表达式分为不同的簇,为调节相似度计算中参数提供依据。再使用遗传算法对参数进行优化,使得相似度计算结果更加准确。
本文使用K-means++聚类算法,将数学表达式聚类到不同的侧重点簇中,充分体现数学表达式主要框架结构对相似度计算的影响,以获得更加准确的匹配结果。将表达式所属侧重点簇作为依据,使用遗传算法对相似度计算中相关参数进行调节,提高了方法的灵活性,使其更好地适用于不同侧重点表达式的相似度计算。该方法提高了数学表达式相似度计算的准确性,使其更好地服务于信息检索,使用户得到的检索结果更加理想。
1 数学表达式相似度计算方法
1.1 数学表达式相似度计算总体思路
基于侧重点聚类的数学表达式相似度计算方法总体流程分两部分,如图1所示。聚类部分使用K-means++聚类算法对数据集进行聚类,根据表达式侧重点不同将其分为不同的侧重点簇,并且确定各个侧重点簇的聚类中心。参数调节部分,首先使用Jaccard 相似度计算方法[18],计算表达式间相似度,获取初始结果列表。接着根据聚类结果对查询表达式和结果列表中表达式的所属簇进行判定,并计算结果列表中与查询表达式所属簇相同的表达式所占比例值。最后以该比例值作为适应度函数,使用遗传算法[19-20]调节相似度计算的参数,得到最优相似度结果列表。
1.2 相似度计算方法
本文以数学表达式的MathML 格式为基础,使用XML 解析器将表达式处理为表达式树用于相似度计算。表达式树的每一个节点都存储了表达式的一个运算数或运算符元素,同时对节点中的元素的类别和每个节点的所在层次、所在层次中的排序等位置信息都有所标记。
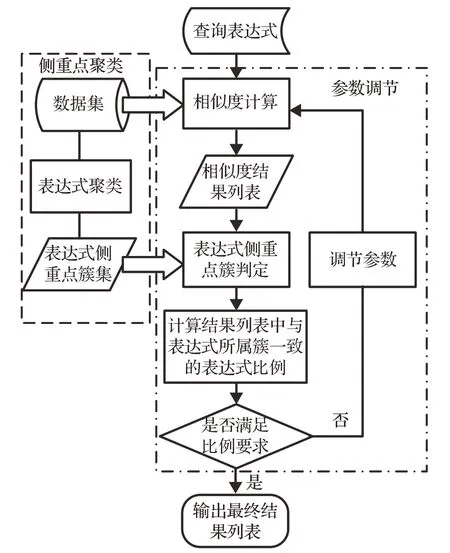
图1 数学表达式相似度计算总体流程图
使用Subtree Hash、Modular Trick、SIGURE Hash三种哈希算法分别对表达式树进行初步处理,计算公式如(1)~(4)所示:
Subtree Hash:

Modular Trick:

其中p、b、s满足:

SIGURE Hash:

其中,l表示公式树的层数,祖先节点为0 层,叶子节点为第l-1 层;n为该节点孩子节点个数,i为节点所在层次的节点个数;s表示子树可以散列到期望的深度,1 <s≤l;xli表示第l层的第i个节点。hash(xli)、hash()分别表示第l层的第i个节点在数据字典中对应的哈希值和其经过计算后得到的哈希值。hash()表示计算后根节点的哈希值,即为该哈希算法对表达式处理的最终值,该值由叶子节点自底向上计算而来,叶子节点的hash(x)值和hash(x′)值相同。
p、b为预设置参数,二者对哈希计算结果都有着直接影响。其中,参数b用于捕捉数学表达式中结构或者模式的语义,仅对于Modular Trick有影响,根据公式(3)可知其值可由p决定;参数p涉及到的运算主要为求余运算,其取值范围为1 <p≤H,H为公式(1)与公式(2)中被除数的较小值,参数p的确定是表达式相似度计算的关键。
最后通过Jaccard算法初步计算出两个公式间的相似度J(M1,M2):

其中M1、M2分别为参与相似度计算表达式的Subtree Hash、Modular Trick、SIGURE Hash三种哈希计算得到的最终哈希值集合。
1.3 基于K-means++聚类算法的侧重点簇判定
表达式侧重点簇的判定是参数调节的依据,为了解决侧重点概念主观性强、难以人为归纳的问题,对表达式元素的映射规则进行定义,使用K-means++聚类算法对表达式的侧重点簇进行判定。
本文在K-means++聚类计算时舍弃了存储运算数的叶子节点,层次遍历标记树中的非叶子节点。表达式之间距离D(X,Y)如公式(6)所示:
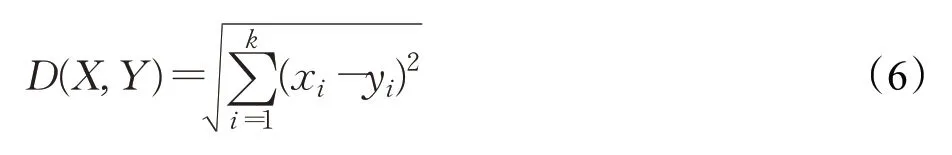
其中,xi、yi分别为X、Y两棵表达式树的非叶子节点的映射值,i为表达式树非叶子节点个数,取两棵表达式树中的非叶子节点个数较大的值。
表达式树中节点元素的映射规则为:
(1)子节点数目不同的节点映射为不同值。
(2)若子节点数目相同,根据子节点顺序是否可调换映射为不同值。
以图2中(a)、(b)、(c)、(d)四棵表达式树为例:表达式树(d)根节点的子节点数目与前三个表达式树根节点的子节点数目不同;表达式树(c)与前两个表达式树的子节点数目相同,但其两个子节点顺序不可调换而(a)、(b)的子节点顺序是可以调换的。则在聚类计算中将+、×都映射为α,÷、∑分别映射为β、γ。

图2 表达式树
对一个数学表达式树节点映射后,数学表达式的侧重点使用K-means++聚类计算进行归纳。聚类过程如下所示:
(1)从数据集中随机选择一个样本表达式作为第一个聚类中心A1。
(2)计算数据集中每一个样本表达式与当前已有聚类中心之间的最短距离,用minD(X)表示。
(4)重复步骤(3)直至选择出所有的初始聚类中心。
(5)计算每个样本点到各个初始聚类中心的距离,将其归纳为与其距离最近的聚类中心簇中,进行迭代。
(6)迭代过程中,使用均值法更新各个簇的聚类中心,当聚类中心变化趋近于稳定状态时,迭代结束,聚类完成。
通过计算表达式到每个聚类中心的距离,以距离最近的聚类中心的所属簇作为表达式的侧重点簇,完成对表达式侧重点簇的判定。
1.4 基于遗传算法的参数调节
不同的参数p进行相似度计算得到不同的结果列表,参数p的值决定了结果列表中与查询表达式所属簇相同的表达式的比例,而该比例决定了此时的参数p是否为最优解。
本文使用遗传算法对表达式相似度计算方法中的参数p进行调节,确定其范围内的最优取值,使得到的计算结果中表达式与查询表达式所属簇一致性最高。
将参数p在其范围内的可选值作为染色体,这些染色体随机组成的M个种群P(0)作为初始化种群。使用结果列表中表达式与查询表达式侧重点簇一致的比例作为适应度函数,评价染色体的适应度高低,适应度函数设置为公式(7):

其中,f为染色体适应度值,y为结果列表中与查询表达式类型一致的表达式个数,Y为结果列表中表达式个数(本文取前100),二者比例越高染色体适应度越高。在对染色体适应度进行评价后,对其进行选择、交叉、变异处理。选择的目的是将适应度高的个体直接遗传到下一代,使用比例选择方法对个体进行选择,即个体被选中的概率Pi与其适应度成正比,如公式(8)所示。N为群体中个体数量,fi为个体的适应度。


表1 提取表达式及其相关信息示例
采用自适应方法对交叉概率Pc和变异概率Pm进行计算,计算公式分别如公式(9)和公式(10)所示:
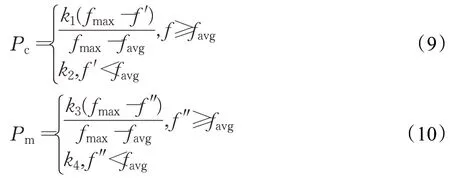
其中,fmax为种群中的最大适应值;favg为种群平均适应值;f′、f″表示将要交叉或变异的两个染色体中较大的适应度值;k1、k2、k3、k4为常数,本文中k1、k3取值设置为0.5,k2、k4取值设置为0.97[21]。
本文设置算法最大迭代次数为500,当在迭代次数内最优个体适应度达到70%时或到达最大迭代次数时,算法终止。得到最优的参数p,从而输出该参数下的相似度计算结果列表。
2 实验结果与分析
2.1 实验设备与数据集
实验主要开发工具为Visual Studio 2017,编程语言为 C#。实验环境为:CPU Intel®CoreTMi5-4570,3.20 GHz,内存8 GB,系统环境为Microsoft Windows10。
本文实验数据集为NTCIR-12-MathIR-Wikipedia-Corpus,共采集31 401篇文档。对数据集文档进行预处理,数据集中表达式的表现形式有两种分别为:MathMLPresentation、MathML-Content,提取其中Content部分用于本实验,共提取373 615个数学表达式,提取表达式示例如表1所示。
2.2 数学表达式聚类结果
在基于K-means++聚类算法对表达式侧重点簇的归纳中,通过不断进行实验和对结果的分析,当K值为9时,簇间距离适中,各个侧重点簇间区别较为明显,聚类效果最佳,表达式聚类结果数据如表2所示。
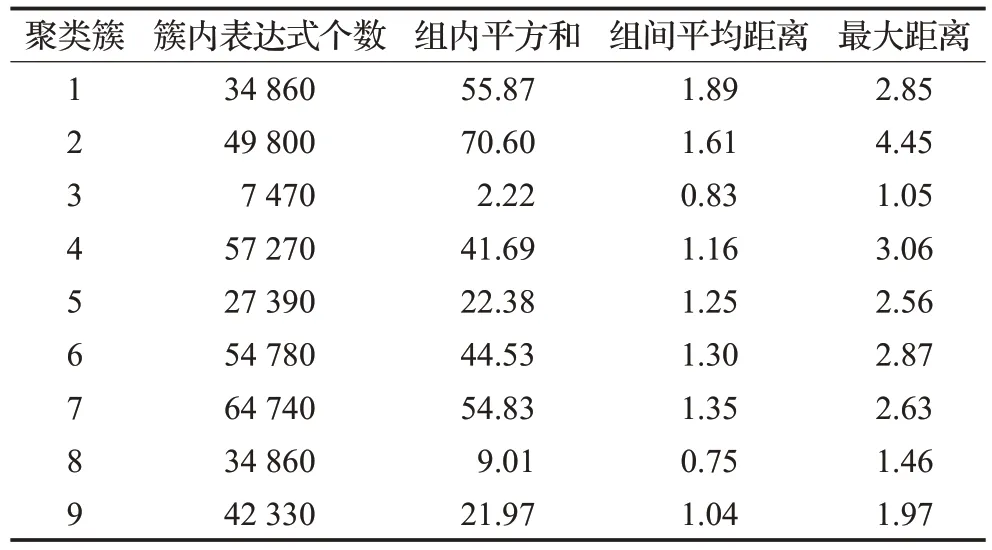
表2 聚类结果数据表
2.3 对比实验及数据分析
本文与文献[12]的方法进行对比实验,以公式(11)为例,从相似度计算结果、相似度计算性能、响应时间三个方面进行对比分析。

2.3.1 相似度评价指标
本文使用F1-Score 对相似度计算效果进行评估。F1-Score是精确率和召回率的调和平均数,如公式(12)~(14)所示,其中pr为平均精确率,re为平均召回率,T(i)为相似度结果列表中表达式,R(i)为专家标记认证符合查询表达式相似度的表达式。F1 的取值范围为[0,1],其值越接近1说明形似度计算效果越好。


表3 相似度计算Top-5结果列表

2.3.2 相似度计算结果
本实验与文献[12]的相似度计算结果TOP-5列表如表3所示,本文方法中Top-2表达式与查询表达式相同,表现形式不同,排名靠前,但并未出现在文献[12]的前5个结果表达式中。可以看出本文方法可以使得表现形式不同的相同表达式排名靠前,得到更加精确的相似度计算结果。
2.3.3 相似度计算性能分析
表4为两种实验方法对5组表达式进行计算得到的相似度结果列表的F1-Score的数据对比。文献[12]的平均F1-Score为0.76,而本文的平均F1-Score为0.84,相比于对比实验提高了0.08,说明本文方法通过对表达式侧重点的聚类,判定表达式的侧重点簇有效地改善了相似度计算结果。

表4 F1-Score对比表
2.3.4 相似度计算响应时间
本文与文献[12]响应时间对比如图3所示。
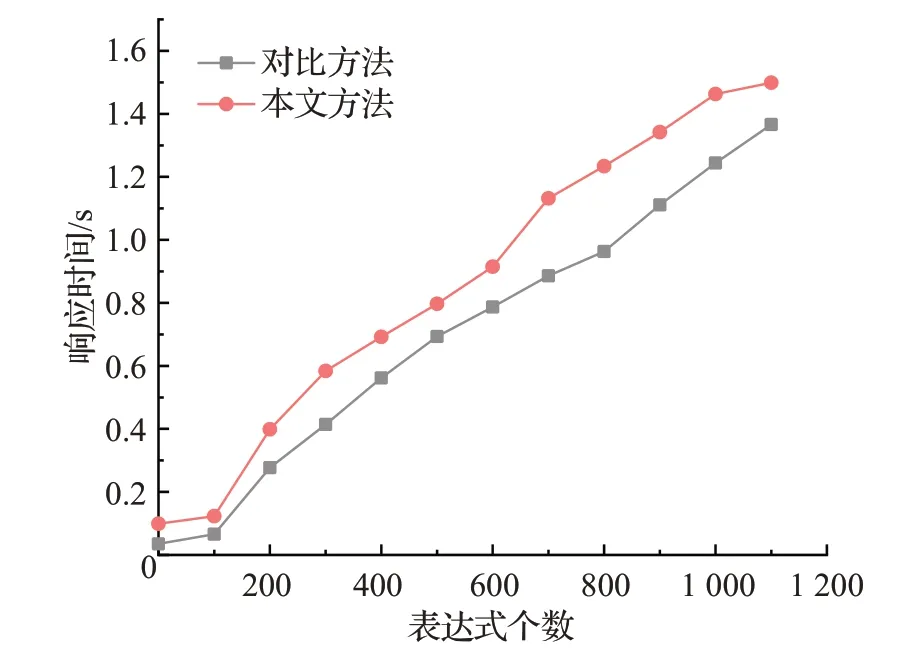
图3 响应时间对比
经过对比可以看出,虽然本文的响应时间较慢,但二者的响应时间差别并不大,可以在合理的时间内得到所需表达式相似度计算结果。本文牺牲可接受范围内的时间,对表达式侧重点聚类以及对侧重点簇判定,对相似度计算中参数进行调节,使得与查询表达式一致性更高的结果表达式排名靠前,方便用户得到更加理想的结果表达式。
3 结语
本文从表达式的侧重点出发,提出了一种基于侧重点聚类的数学表达式相似度计算方法。对数据集中表达式进行侧重点聚类,通过计算相似度结果列表与查询表达式所属相同簇的比例,得到参数调节的依据,优化调节参数,得到最终的相似度结果列表。该方法体现了表达式结构框架对相似度计算的影响,增加了数学表达式相似度计算的灵活性。通过多次实验以及对实验结果的分析,确定合适的K值和遗传算法中的相关参数值,从实验结果分析可以得到,平均F1-Score 达到了0.84,较对比实验提高了0.08,表明本文的相似度计算方法相似度计算性能好,提高了信息检索的准确性。但本文只针对于数学表达式的MathML格式,并未考虑到其他格式下表达式的相关计算情况;且本文进行聚类的数据集与相似度计算使用数据集为同一数据集,较为单一。进一步会尝试对不同格式数学表达式进行应用,考虑不同数据集中的实验效果,对算法进行改进。

