采用DDPG的双足机器人自学习步态规划方法

周友行，赵晗妘，刘汉江，李昱泽，肖雨琴

湘潭大学 机械工程学院，湖南 湘潭 411105

步态规划是机器人控制领域的研究热点和重要的研究内容。双足机器人结构复杂，其行走过程是由连续的摆腿和离散的碰撞组成，具有众多自由度，难以通过传统控制理论方法建立动力学模型[1]。即便勉强采用此类方法，也会导致双足机器人运动过程消耗大，行走速度低，环境适应性差。实际上相比精准的步态，功能性和抗干扰性更为重要，也能使双足机器人能面对不同环境的需求。

随着信息技术的发展，以强化学习为代表的智能算法以其自适应特性越来越多运用于机器人控制领域[2-3]，但过去强化学习在机器人控制领域的实践都局限于低维的状态空间和动作空间，且一般是离散的情境下。然而现实世界的复杂任务通常有着高维的状态空间和连续的动作空间。2013 年，DeepMind 团队提出了结合深度神经网络和强化学习的DQN算法[4]，解决了高维输入问题。但DQN 仍是一个面向离散控制的算法，对连续动作处理能力不足。在机器人的实际控制中，每个关节的角度输出是连续值，若把每个关节角取值范围离散化，则行为的数量随自由度的数量呈指数增长。若进一步提升这个精度，取值的数量将成倍增长。

为了将DQN 拓展到连续控制领域，众多学者展开了研究，目前来看，顾世翔等提出的NAF[5]和DeepMind提出的DDPG[6]是有效的解决方案，但相比这两种算法，NAF实现起来过于复杂，DDPG则是基于Actor-Critic方法[7]，包含一个策略网络（Actor）用来生成动作，一个价值网络（Critic）用来评判动作的好坏，并吸取DQN 的优秀特性，同样使用了样本经验回放池和固定目标网络[8]。

尽管DDPG学习算法已经接近于现实应用，但考虑到双足机器人模型的复杂度和动态规划对实时性的要求，仍有进行优化的必要。因此，提出一种自学习步态规划算法，在DDPG 算法的基础上，将具有局部映射特性的RBF 神经网络运用于DDPG 中非线性函数的计算[9]，提高学习收敛速度。然后采用梯度下降算法更新神经网络权值，采用SumTree 来筛选样本，进一步提高算法的效率。最后在Gazebo环境中对双足机器人进行了模拟学习训练，经数据仿真表明，该算法能使双足机器人自主学习稳定自然的动态行走[10-11]。

1 机器人模型描述

以如图1 所示双足步行机器人为例展开研究。机器人左右对称，由七个部分组成：两大腿、两小腿、两足和一个躯干。由于躯干以上部分对行走过程的影响相对下肢较小，因此在研究过程抽象成质心和转动惯量不变的连杆，只在模拟过程加入适量扰动模拟双臂摆动对步行过程稳定性的影响。

图1 双足机器人模型

双足机器人包含8 个自由度：两个髋关节4 个自由度，两个膝关节2个自由度，两踝关节2个自由度。各关节自由度在笛卡尔坐标系中的分布方式如图2所示。

双足机器人样机基本参数如表1所示。

表1 双足机器人样机参数

图2 双足机器人各关节自由度分布

由于在人类步行过程中，以矢状面的屈伸运动为主导，包括髋、膝的屈伸运动，而冠状面的活动对行走过程影响较少。因此在实际步态分析中，主要考虑髋关节和膝关节的数据结果[12]。

矢状面关节上的屈伸范围如表2所示。

表2 矢状面上各关节转矩和最大屈伸范围

2 DDPG算法原理

利用智能体与环境交互所得的奖惩信息来指导智能体的行为的策略，叫做强化学习。DDPG是强化学习中基于Actor-Critic 的算法，它的核心思想是利用Actor网络用来生成智能体的行为策略，Critic 网络来评判动作好坏，并指导动作的更新方向。如图3所示，DDPG结构中包含一个参数为θπ的Actor 网络和一个参数为θQ的Critic 网络来分别计算确定性策略a=π(s|θπ)和动作价值函数Q(s,a|θQ)[13]。由于单个网络学习过程并不稳定，因此借鉴了DQN 固定目标网络的成功经验，将Actor 网络和Critic 网络又各自细分为一个现实网络和一个目标网络。现实网络和目标网络结构相同，目标网络参数以一定频率由现实网络参数软更新。

图3 DDPG算法结构

现实Critic网络的损失函数为：

其中

m为样本数量，ωj为所采用的不同样本的权重，为样本j在状态为St时采取动作At，通过现实Critic网络计算出来的动作价值，yj为通过样本计算出的目标动作价值，由目标Critic 网络推算得出，Rj为样本j在状态为St时采取动作At获得的即时奖励，γ为折扣因子。

现实Actor网络的损失函数为：

其中，用梯度下降法寻找该损失函数J(θπ)的极小值等价于最大化动作价值的过程。

目标Critic 网络和目标Actor 网络参数采取以下方式更新方式：

τ为更新系数，为避免参数变化幅度过大，范围取0.01～0.1。更新频率为时间步走过1 500次，目标网络更新一次。

3 基于DDPG的算法优化设计

3.1 RBF神经网络近似计算

RBF 神经网络是一种三层神经网络，如图4 所示。由于它的结构简单，且具有局部映射特性，即重点考虑离径向基函数中心近的数据，可以极大减少迭代中需要调整的参数的数量，极大提高了学习收敛的速度，相比较BP神经网络更符合机器人动态步行这一有实时性要求的情景[14]。

图4 RBF神经网络结构图

RBF 神经网络中输入层到隐藏层为权值为1 的全连接，隐藏层到输出层通过权值矩阵相连接。隐藏层神经元的激活函数选用高斯径向基函数，第i个神经元的输出结果为：

其中，βi为扩展常数，x=( )x1,x2,…,xm表示第i个神经元接收到的输入，ci为第i个神经元的核函数中心。

输出层输出结果为：

其中，ωi为隐藏层到输出层的对应权值。

3.2 SumTree作为经验回放池

由于不同样本对训练过程的贡献有所不同，筛选出优质的样本，为提高算法利用率，减少机器人无效的训练次数至关重要。SumTree 作为一个二叉树数据存取结构，已经有学者将其应用于DQN算法的经验回放中，并起到了惊艳的效果[11-12]。在此，也将SumTree 运用于DDPG算法的经验回放中。由于DDPG算法中，策略网络的参数依赖价值网络的选取，而价值网络中的参数由价值网络的损失函数，即目标Q值与现实Q值差值的期望来更新。差值越大，代表网络参数的预测准确度还很远，即该样本更需要被学习，即优先值越高。在此，将目标Q 值与现实Q 值差值的绝对值定为量化样本优先级的标准，设为|δ(t) |。如图5 所示，SumTree 的总容量为399 999，叶节点个数为200 000。叶节点内存放样本的优先级，每个叶节点对应一个索引值，利用索引值，可以实现对应样本的存取。每两个叶节点对应一个上级的父节点，父节点的优先级等于左右两个子节点优先级之和，最后收敛到根节点。

图5 SumTree结构

分别采用两个一维数组来存放优先级和样本池，其中树的结构映射到一维数组的顺序是按从上到下，从左到右展开。存储优先级时，从叶节点开始，即从索引值为199 999开始，每存入一个数据，更新一次与该叶节点相关的父节点的数据以及对应样本池数据。当需要采集样本时，用根节点的优先级（所有叶节点优先级之和）除以样本数m，将优先级按顺序从0到优先级之和分成m个区间。接下来，是在每个区间随机抽取一个数，因为优先级较大的节点也会占据较长的区间，因此被抽到的概率也会较高，这样便达到了最初的目的。每抽到一个叶节点，返回其优先级，及对应的样本池数据。

3.3 算法步骤

输入：环境E，状态空间S，动作空间A。

过程：

（1）初始化 Actor 网络和 Critic 网络，初始化 Sum-Tree并定义容量大小。

（2）从第一回合的第一步开始，进行循环。

①初始化St为当前的第一个状态；

②把状态St作为现实Actor 网络的输入计算，与随机噪声叠加后得到

③执行动作At，得到奖励Rt和新状态St+1；

④将{St,At,Rt,St+1}四元组存入SumTree；

目前，软件缺陷分析统计方法主要包括：柏拉图分析法、根本原因分析法、正交缺陷分类法(Orthogonal Defect Classifica⁃tion，简称ODC)等。其中，利用缺陷正交分类法既可以对缺陷本质特性进行分析，同时又对缺陷类型做了深层次划分，使得该方法既适用于分类缺陷，又能够用来对缺陷进行统计和分析，是目前应用较为广泛的缺陷分析方法[2]。

⑤St=St+1；

⑥ 当len(data)＞m时，从 SumTree 中采集m个样本，其中采样概率依据，权重，计算当前目标Q值：

⑦计算损失函数J(θQ)，利用梯度下降反向更新现实Critic网络的所有参数θQ；

⑧计算损失函数J(θπ)，利用梯度下降反向更新现实Actor网络的所有参数θπ；

⑨重新计算所有样本的误差|δ(t) |，更新SumTree中所有节点的优先值pj=|δj|；

⑩每时间步走过1 500 次，则更新目标Actor 网络和目标Q网络的参数；

4 仿真模拟验证

4.1 仿真环境设计

采用ROS+Gazebo+Tensorflow联合仿真，其中ROS是一个机器人软件平台，充当了仿真器Gazebo 和机器学习平台Tensorflow 的接口。为了简便流程，首先在Solidworks 中建立双足机器人的三维模型并通过SW2URDF 插件导出双足机器人的URDF 文件（统一机器人描述格式），如图6。URDF 文件主要由＜Link＞和＜Joint＞两个标签组成。其中＜Link＞定义了双足机器人的结构件的外观和物理属性，包括形状、尺寸、质量、相对坐标、碰撞参数等，＜Joint＞描述了机器人关节的运动学和动力学属性，包括关节运动的位置和速度限制范围。由于Joint 是用来链接两个Link，因此对每个Joint都必须指定Parent Link 和Child Link。完成URDF 模型的设计后，便可通过ROS功能包的C++解析器解析出文件所描述的机器人模型，也可以通过ROS 中嵌入的可视化工具Rviz显示出来，如图7所示。通过给URDF文件添加＜gazebo＞标签，便可将模型加载到Gazebo 仿真环境。使用Tensorflow创建算法源码，算法相关参数见表3，并将其可执行文件整合到ROS 中，来与机器人模型对接，以实现预定的算法功能。

图6 双足机器人三维模型

图7 ROS中双足机器人模型

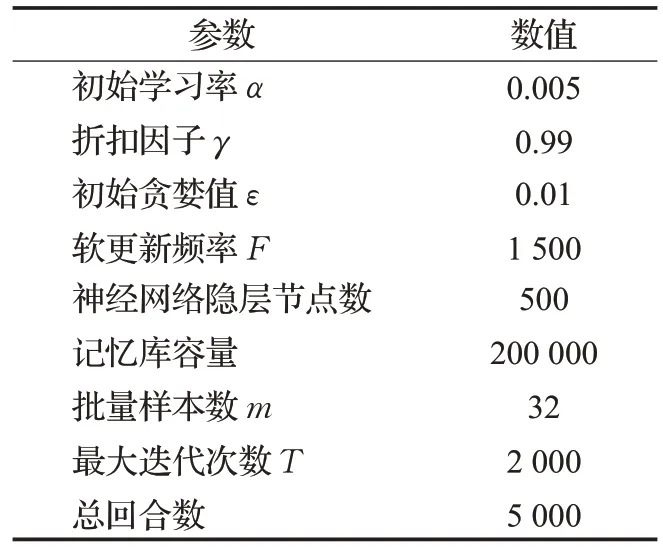
表3 DDPG/DDPG改进算法相关参数

为了验证所提方法的有效性，分别采用DDPG算法和改进后的DDPG 算法进行双足机器人步态规划的模拟仿真，并进行对比分析。根据控制变量法原则，两种情况下均采用相同的仿真环境。在该仿真环境中，机器人要在水平地面上步行完成从起点到终点总长88 m的距离的任务，每一次成功到达终点或中途倒下，一个回合结束。关节的转矩和角度范围限定如上文所述。摩擦力系数为0.5，设立旋转副的位置，并在动作上施加适度扰动，设置状态为质心速度，关节位置和关节角速度，腿与地面接触等参数，利用相对坐标系将机器人的6个关节每个关节的转角按弧度划分为(-1,1)，动作为6个关节的转角数组，当机器人到达目标位置或者机器人倒下时，系统复位。总训练回合数为5 000次。

4.2 结果分析

图8为两种算法每平均100回合中所取得平均累积奖励曲线对比，累积奖励越高，代表机器人按照期待的目标选出来更优的动作。从图上看来，两条曲线都呈递增趋势，且当训练回合超过某一定值后，均趋于稳定。但是比较表4数据，DDPG算法用了4 323回合到达最大累积奖励，而改进后的DDPG 算法迭代2 037 次即到达最大累积奖励，比前者提升了45.7%。可见，RBF 改进后的DDPG算法具有更高的效率。

图8 两种算法所取得累积奖励对比

表4 求解迭代总次数比较

图9为两种算法下机器人每平均100回合中成功步行到达的距离曲线对比。可以看到，在训练初期，上升速度较快，但学习程度不够充分，且随机性大，成功几率小。且前期为了充分遍历，找到最优策略，探索率比较高，受到环境干扰的影响，曲线波动较大，随训练次数增加，探索率减少，充分学习后，机器人由探索环境的状态逐步转为利用经验知识的状态，成功率瞬间升高并趋于稳定。2 000 回合以后，机器人能步行到的距离也更加稳定，愈来愈接近于给定值。比较表5 数据，可以看到两种算法在给定任务的执行力上有较大区别，在仿真的5 000 回合中，用DDPG 算法下机器人到达终点的次数为102次，成功率为2.04%，用改进后的DDPG算法成功次数为547次，成功率10.94%，提高了8.9个百分点。

图9 两种算法步行到达距离对比

表5 成功率比较

图10、图11 为 DDPG 算法及 DDPG 改进算法下机器人均达到规律周期运动后的髋、膝关节的姿态角度对比。从关节的顺畅性，平稳度来看，在使用改进后的DDPG算法相比改进前具有更好的效果。

5 结论

（1）针对双足机器人步行控制中高维非线性规划难题，提出一种基于DDPG 的深度强化学习算法，来解决双足机器人步行控制中高维非线性规划难题，从动力学角度出发对双足机器人步行进行动态控制。利用RBF神经网络的局部映射特效，来提高DDPG算法的学习速度，采用梯度下降算法更新神经网络权值，并采用Sum-Tree来筛选优先级别高的样本，进一步提高权值的更新速度。

图10 DDPG算法关节姿态角度曲线对比

图11 DDPG改进算法关节姿态角度曲线对比

（2）运用所提出方法对双足机器人的步行过程进行仿真模拟，结果显示机器人平均达到最大累积奖励的时间提前了45.7%，成功率也提升了8.9个百分点，且改进后的DDPG 算法训练下的各关节力矩、角度变化平稳，且较好贴合预定运动轨迹，证明了该方法的有效性。