自调节式手腕康复外骨骼机构设计与相容性分析*

王传伟，单 泉，陈 砚，张荣闯

(东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004)

0 引 言

腕关节是前臂与手的重要连接关节，在上肢运动中起着重要作用。脑卒中疾病引起的腕关节运动功能障碍，严重影响患者的日常生活。而使用康复机器人治疗脑卒中疾病引起的肢体运动障碍已被证实是有效的，因此，设计研发手腕康复外骨机构具有现实意义[1-2]。

目前，外骨骼机构设计通常是模仿人类肢体关节的运动，但由于人机初始穿戴偏差、人类个体之间的差异及人体关节运动的复杂性等因素的影响，使得外骨骼关节的运动无法精确复制人体关节的运动，从而在康复训练中产生与训练无关的约束力或力矩，导致康复训练时舒适性变差，影响康复效果，这一现象称为人机运动不相容现象[3-5]。

针对这一现象，学者们对腕关节康复机器人展开了深入研究。意大利理工学院MASIA L等[6]提出了一种三轴驱动手腕康复机器人，通过在手柄连杆上增加一个被动移动副，来补偿人机在手臂轴线方向的偏差;美国西北大学BEEKHUIS J H等[7]研制了一款自对准式平行四边形机构手腕康复机器人，它在人机界面处增加具有被动副的平行四边形机构，该机构通过被动副的移动来调节平行四边行4条边相对角度的变化，从而实现了与人体手腕关节与机器人关节在单一平面内的对齐；新加坡南洋理工大学ESMAEILI M等[8]设计的单轴手腕康复机器人，具有两个被动移动副与两个被动转动副，成功弥补了人机运动空间内的角度与位置偏差，实现了单轴手腕康复机器人的人机相容性。

综上所述，腕关节康复机器人主要通过增加被动副，依靠被动副产生一定范围位移与角度的平滑运动来补偿人机关节误差，从而实现了人机相容性。

本文设计一款3RPPR型三轴驱动手腕康复外骨骼机构，通过3个主动转动副的运动实现人体腕关节的三自由度康复运动，并通过两个被动移动副与一个被动转动副的运动实现人体腕关节在康复运动中的人机相容性。

1 人体腕关节运动分析

腕关节是完成上肢功能的主要部分，由桡腕关节、腕骨间关节、掌腕关节组成。因人体腕关节的运动较为复杂，在机器人带动人体腕关节进行康复运动时，机器人关节不能像人体腕关节那样灵活的运动。为了满足机器人关节与人体腕关节的相互对应关系，需要适当简化人体腕关节的运动：

首先，忽略前臂内旋/外旋运动中旋转轴的位置变化，并将前臂的内旋/外旋运动等效为腕关节的内旋/外旋运动；其次，忽略腕关节掌屈/背屈与桡偏/尺偏两个旋转运动中旋转轴的位置变化，认为掌屈/背屈与桡偏/尺偏的旋转轴是固定不变的，并与腕关节内旋/外旋的旋转轴相交于一个固定的中心点。因此，可将腕关节的运动副简化为3个垂直交于一点的转动副并最终等效为1个球副。

手腕运动方式等效图如图1所示。

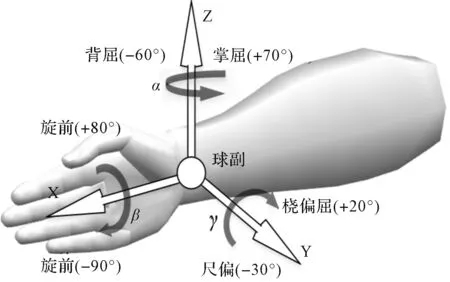
图1 手腕运动方式等效图

图1中，基于上述分析可知，人体腕关节可分别绕X轴、Y轴与Z轴做单轴旋转运动，并且为了确保人体腕关节进行安全有效的康复训练，手腕康复机构的最大运动角度范围不能超出人体腕关节允许的最大角度范围[9，10]。

2 腕关节机构构型及其类型选择

2.1 腕关节机构自由度分析

外骨骼机器人在带动人体腕关节康复运动时，形成人机闭链机构。JARRASSE N等[3]根据高等空间机构学理论，研究出了一种人机闭链被动自由度的计算方法。

笔者采用该方法建立腕关节人机闭链模型图，如图2所示。

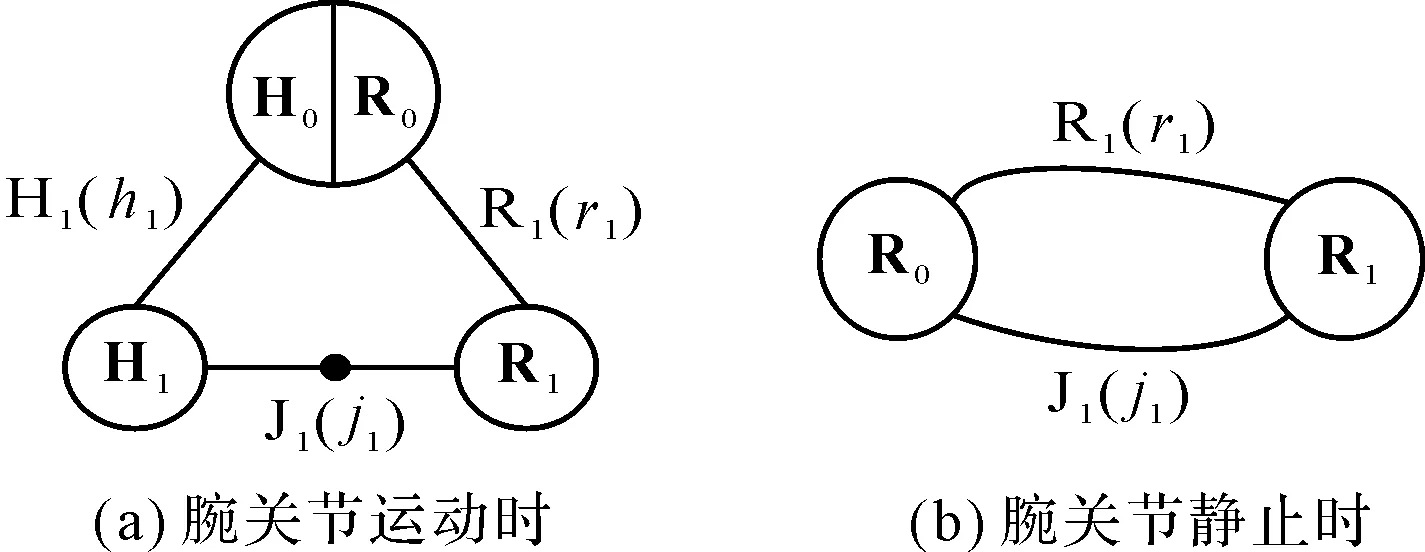
图2 腕关节人机闭链模型图H0—人体前臂肘部；R0—康复机构基座；H1—人体手部；R1—康复机构主动关节链与被动关节链连接件；H1—人体前臂；h1—前臂腕关节自由度数；R1—康复机构；r1—康复机构主动关节自由度数；J1—被动关节链；j1—康复机构被动关节自由度数

假定人体前臂肘部与康复机构基座固连，则H0与R0是固连的。H1与R1之间通过J1连接。设计J1时，需要满足人体前臂静止时外骨骼不能自由运动，因此可将图2(a)简化为图2(b)；并可由满足人机相容的情况下，人机闭链为单环时自由度数为6[3]推导出下式：

j1+r1=6

(1)

由于外骨骼机构关节与人体关节对应，可推出腕关节主动自由度r1=h1=3；将其代入式(1)得到被动自由度数：

j1=6-r1=6-3=3

(2)

2.2 腕关节机构构型

人机闭链构型的方式有两种：(1)在机器人关节处添加被动副，通过被动副的运动使机器人关节与人体关节始终处于对齐状态，来满足人机相容性需求的自跟踪式；(2)在机器人与人体连接处添加被动副，通过被动副的运动使机器人关节与人体关节不需对齐，就能满足人机相容性需求的自调节式。

相比自调节式构型的机器人，自跟踪式构型的机器人存在控制难度大，及在使用被动副调节人机关节的相互位置时，会产生更大的无效力/力矩等缺点[11]，此处拟采用自调节式构型的方式来设计人机闭链机构。

自调节式腕关节机构构型如表1所示[12，13]。

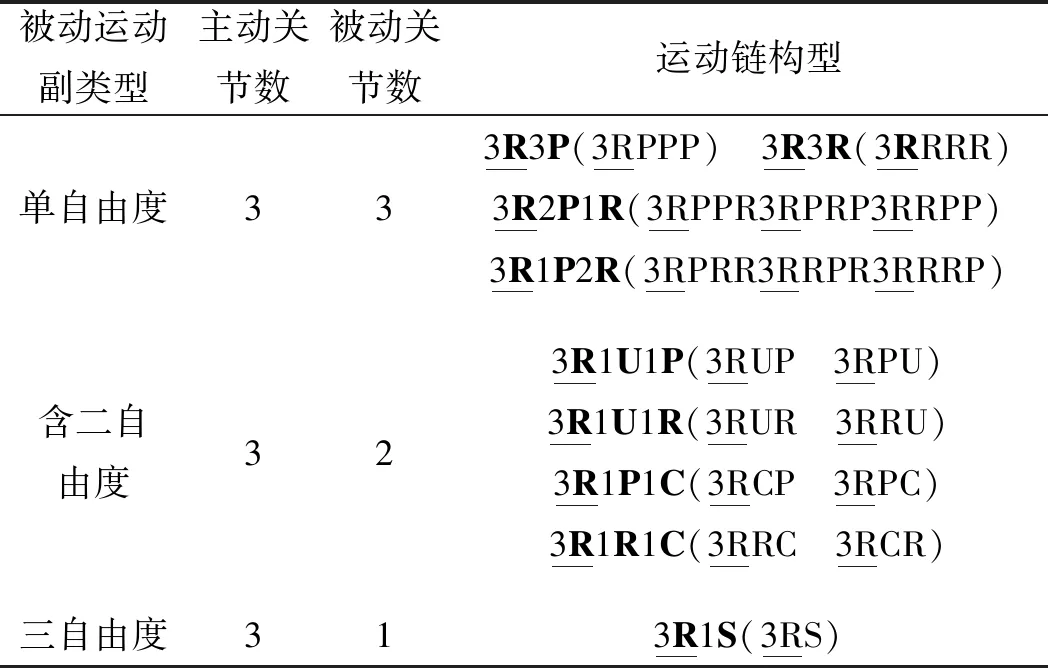
表1 自调节式腕关节机构构型

表1中，按被动运动副种类，可将外骨骼腕关节机构分为单自由度、含二自由与三自由度三类，分别对应6个关节(3个主动关节，3个被动关节)，5个关节(3个主动关节，2个被动关节)与4个关节(3个主动关节，1个被动关节)。在不考虑被动副连接位置与次序时，共有9种代表构型(表1中加粗字体表示)；在考虑被动副连接次序时，共有17种具体构型(表1括号内字母表示)。

2.3 腕关节机构构型类型选择

由于腕关节机构构型种类较多，笔者选择了部分有工程价值的代表构型，建立腕关节机构构型简图，如图3所示。

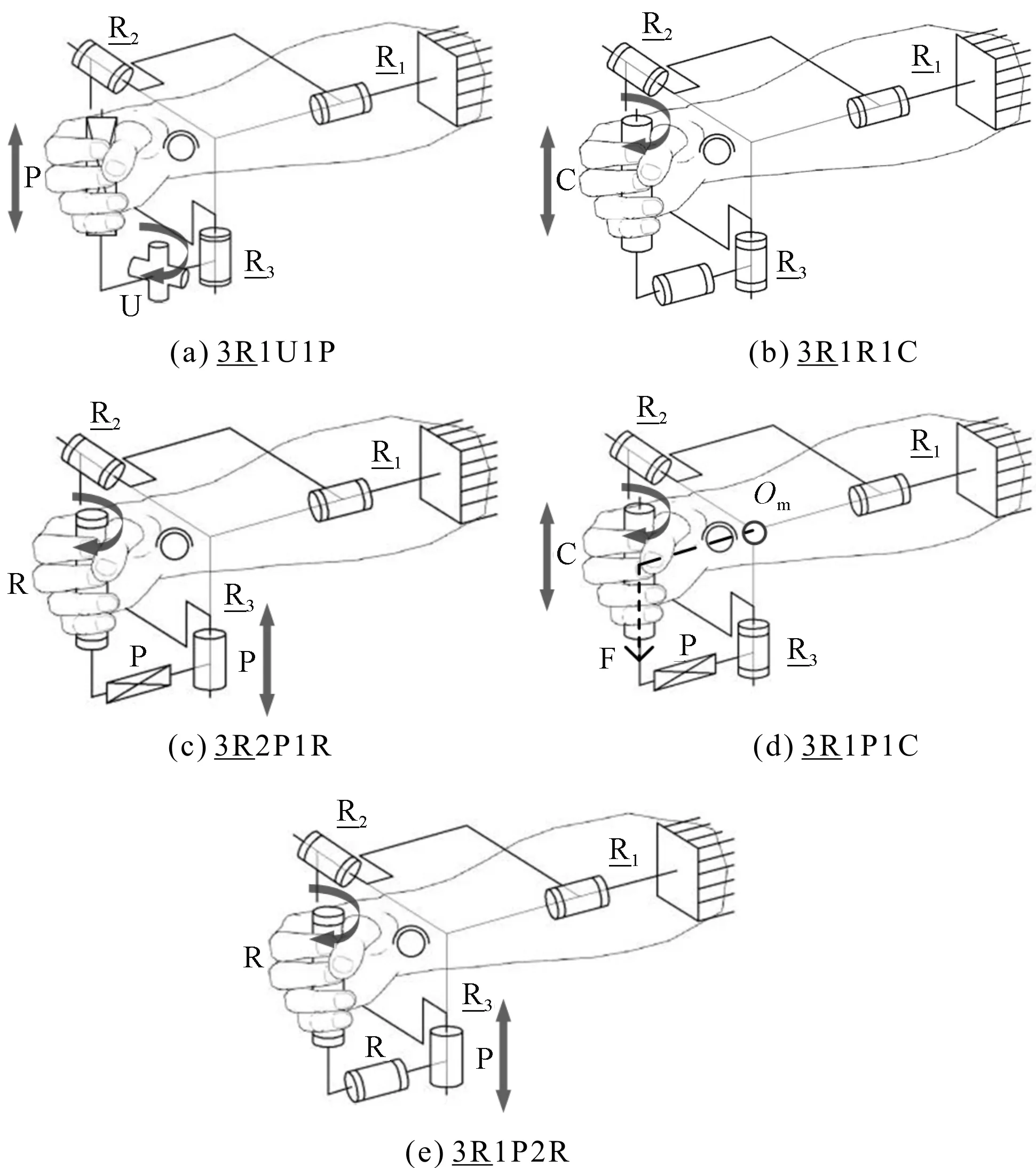
图3 腕关节机构构型简图

图3中，各构型通过引入被动关节，来释放这种与训练无关的力与力矩，黑色实心箭头方向即为释放方向。可以看出：各机构构型既可释放沿轴线方向的力，又可释放绕轴线方向的力矩。但在主动副带动人体运动时，由于被动副对力或力矩的释放作用，在有些机构中阻碍了有用力或力矩的传递，因此，需要对图3中各机构进行受力分析。

如图3(d)中3R1P1C所示，当R2带动手柄一起绕转圆心Om转动时，如果手柄不含有运动副，此时手柄受到与圆心Om垂直的力F，因此，可带动人手做桡偏/尺偏康复运动；如果手柄含有移动副P或圆柱副C，此时由于这两种运动副在力F方向存在移动，而无法将力F传递到手柄，因此，手柄不能带动人手运动。

综上所述，若想使手柄带动人手做桡偏/尺偏康复运动，则手柄不能含有P副或C副，故将图3(a)中3R1U1P、图3(b)中3R1R1C及图3(d)中3R1P1C排除。

此外，由于图3(c)中3R2P1R与其手柄相连移动副P可直接消除腕关节与康复平台沿移动副P运动方向的穿戴偏差，而图3(e)中3R1P2R需要多运动副共同作用，才能消除手腕与康复平台沿移动副P运动方向的穿戴偏差。因此，为简化康复平台各关节运动，笔者最终选择了图3(c)3R2P1R作为康复平台的设计机构。

3 人机闭链相容性分析

3.1 机构支链运动方程的建立

人体腕关节康复运动时，3RPPR机构(机构支链)与人体前臂(人体支链)形成人机闭链系统，根据右手直角笛卡尔准则，对人机闭链各运动关节建立坐标系。

3RPPR坐标系图如图4所示。

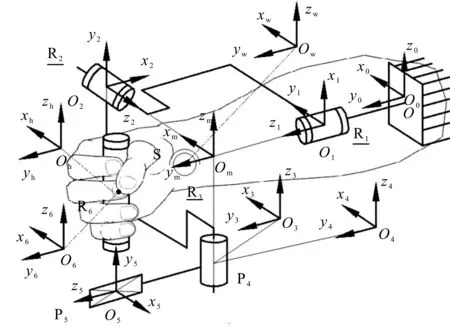
图4 3RPPR坐标系图O0—人体手臂原点(人机闭链坐标系的参考点)；O—康复平台的原点；O0x0y0z0—人机闭链固定坐标系；Owxwywzw—人体腕部球关节坐标系；Ohxhyhzh—转动副R6与手部中心坐标系；O1x1y1z1，O2x2y2z2，O3x3y3z3—主动副的主动坐标系；Omxmymzm—机构腕部球关节坐标系(3个主动副中心轴的交点)；O4x4y4z4，O5x5y5z5，O6x6y6—被动副的被动坐标系

3RPPR机构尺寸表示图如图5所示。

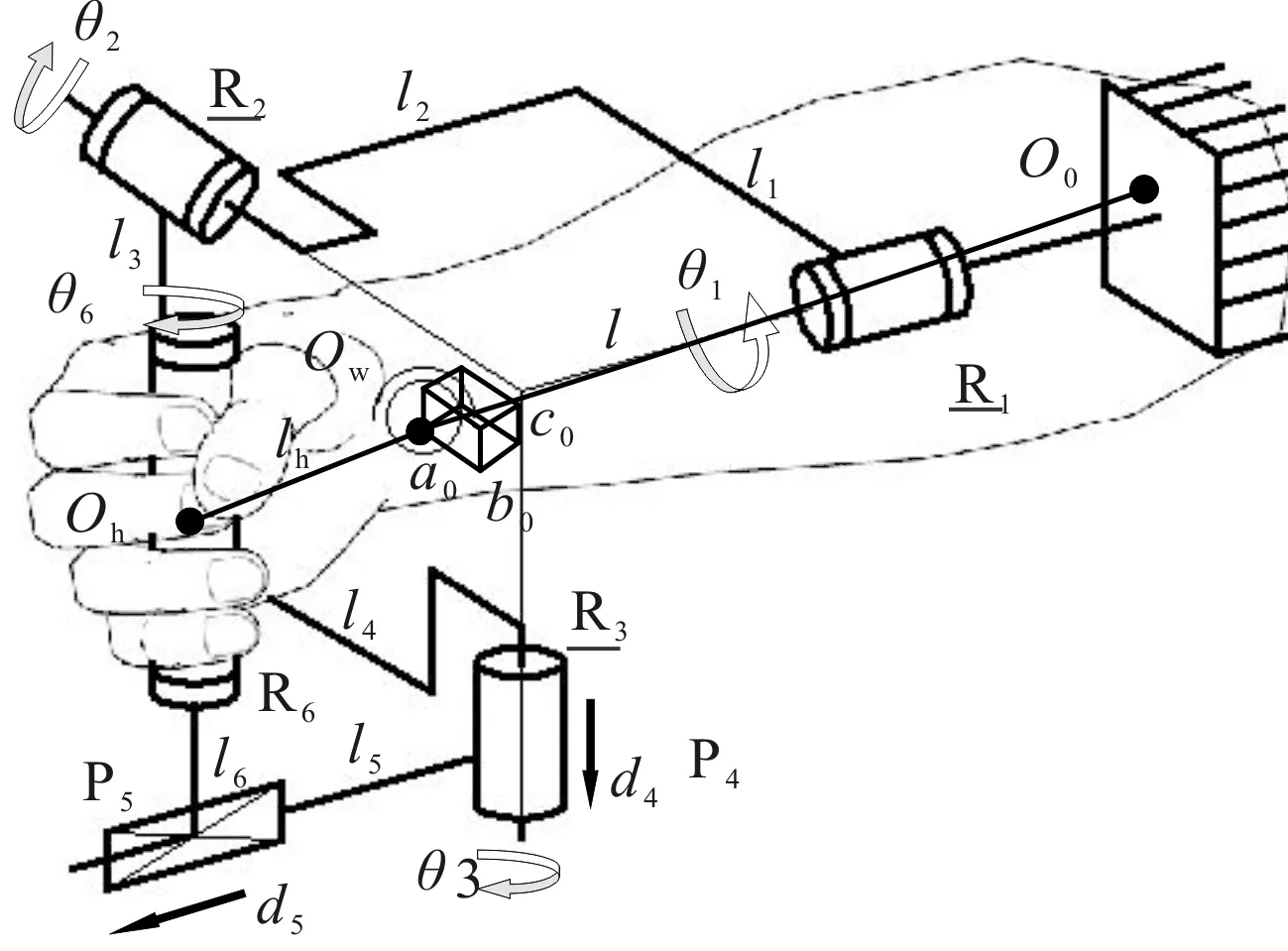
图5 3RPPR机构尺寸符号图a0，b0，c0—人体腕关节与康复机构穿戴偏差；θ1—R1的转角；θ2—R2的转角；θ3—R3的转角；θ6—R6的转角；l—人体手臂原点O0到人体腕部Ow的距离；l1，l2，l3，l4，l5，l6—机构各个关节间距离；d4—P4的移动距离；d5—P5的移动距离；lh—手部中心Oh到人体腕部Ow的距离

对于机构支链，机构末端转动关节R6的被动坐标系O6x6y6z6相对于固定坐标系O0x0y0z0的位姿变换矩阵0T6为：

(3)

式中：jTi—坐标系Oixiyizi相对于坐标系Ojxjyjzj的位姿变换矩阵(i=1～6，m；j=0～5，m)；(n6xn6xn6x)T—x6轴的方向矢量；(o6xo6xo6x)T—y6轴的方向矢量；(a6xa6xa6x)T—z6轴的方向矢量；(X6Y6Z6)T—康复机构末端关节转动副R6中点位置矢量。

0T6中各相乘矩阵表示如下：

(4)

式中：s—sin；c—cos。

3.2 人体支链运动方程的建立

对于人体支链，手部中心坐标系Ohxhyhzh相对于固定坐标系O0x0y0z0的位姿变换矩阵0Th可表示为：

(5)

式中：0Tw—坐标系Owxwywzw相对于坐标系O0x0y0z0的位姿变换矩阵；wTh—坐标系Ohxhyhzh相对于坐标系Owxwywzw的位姿变换矩阵；(nhxnhxnhx)T—xh轴的方向矢量；(ohxohxohx)T—yh轴的方向矢量；(ahxahxahx)T—zh轴的方向矢量；(XhYhZh)T—为手部中心点位置的矢量。

0Th中各相乘矩阵表示如下：

(6)

式中：α—手腕掌屈/背屈的运动角度；β—旋前/旋后的运动角度；γ—桡偏/尺偏的运动角度。

3.3 人机闭链约束方程的建立及其参数的确立

人体腕关节康复训练时，由于手掌与转动副R6紧密贴合固定，人体手部中心与被动转动副R6中心始终有相同的位姿。因此，可根据机构支链运动方程与人体支链运动方程，推导出人机闭链的运动学约束方程为：

(7)

在第1节中，通过对人体腕关节运动分析可知，腕关节康复训练需要内旋/外旋、掌屈/背屈与桡偏/尺偏三种独立康复运动方式，考虑到患者在痉挛期康复运动范围较小，因此康复训练角度相比人体腕关节正常运动角度范围应适当减小。

康复运动中患者手腕运动角度如表2所示。

表2 康复运动中患者手腕运动角度

确定人体、康复机构尺寸参数与穿戴偏差如表3所示[5]。

表3 人体、康复机构尺寸参数与穿戴偏差

接下来，笔者将人体前臂尺寸、手部尺寸、机构尺寸与人体腕关节各运动方式下运动角度代入约束方程，求逆运动解。

3.4 人机相容性分析及仿真验证

在人机穿戴偏差为定值时，笔者使用MATLAB分别对上述3种康复运动方式的约束方程进行逆解析，可分别得出被动副d4、d5与θ6的变化曲线。由于在掌屈/背屈康复运动中的d4(-10 mm)，旋前/旋后康复运动中的d5(10.5 mm)及桡偏/尺偏康复运动中的θ6(-6.5°)的值基本没有变化(固定值)，所以未使用曲线图表示。

笔者建立的手腕康复平台图如图6所示。

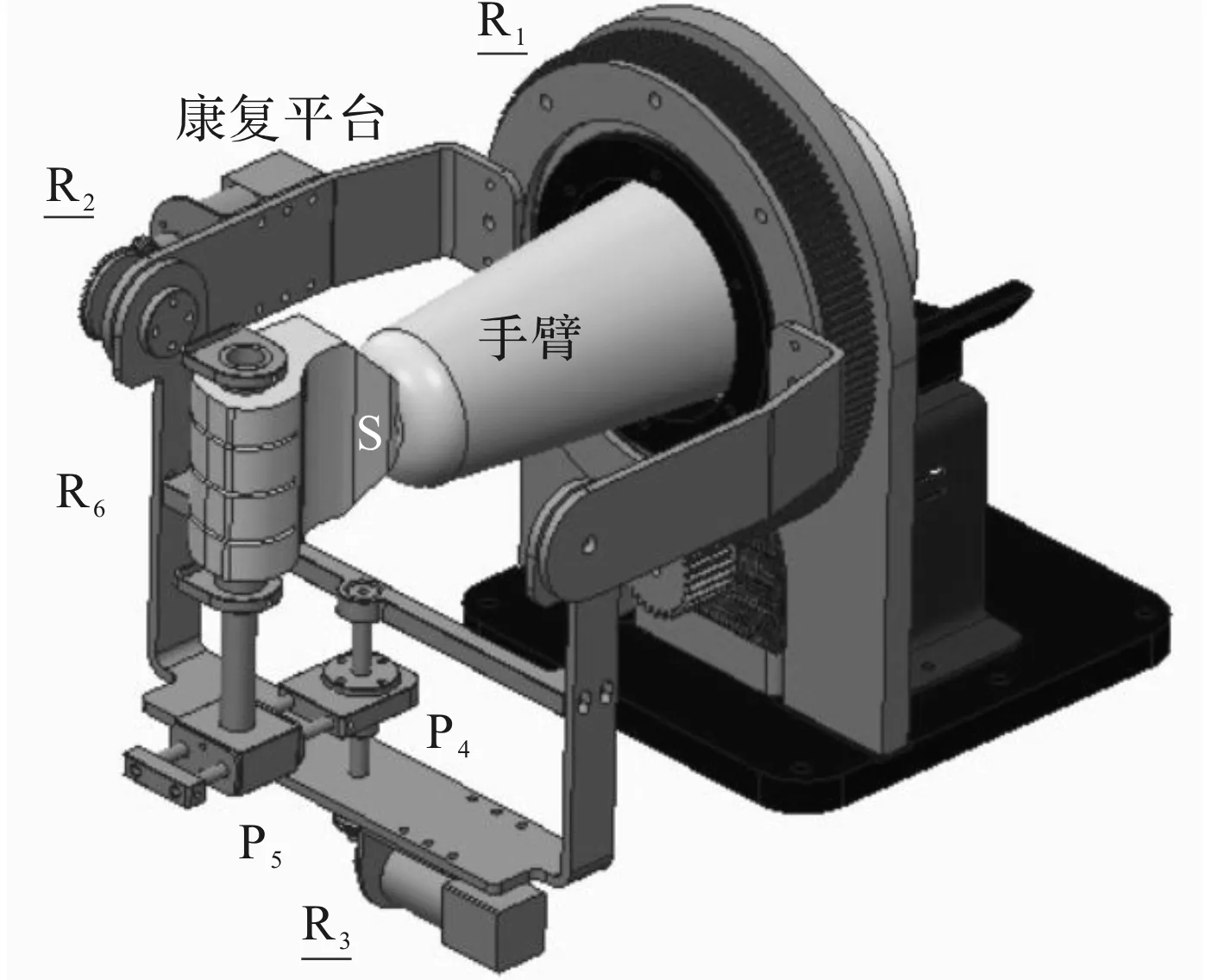
图6 手腕康复平台图

此处笔者通过CREO软件对康复平台进行运动仿真分析，来验证建立的约束方程的正确性。由于康复平台在掌屈/背屈康复运动中的d4(-9.8 mm)，旋前/旋后康复运动中的d5(10.2 mm)，桡偏/尺偏康复运动中的θ6(-6.3°)的值基本没有变化，所以未使用曲线图表示。

其中，通过约束方程解出的与通过康复平台仿真出的被动副运动曲线图，如图7所示。

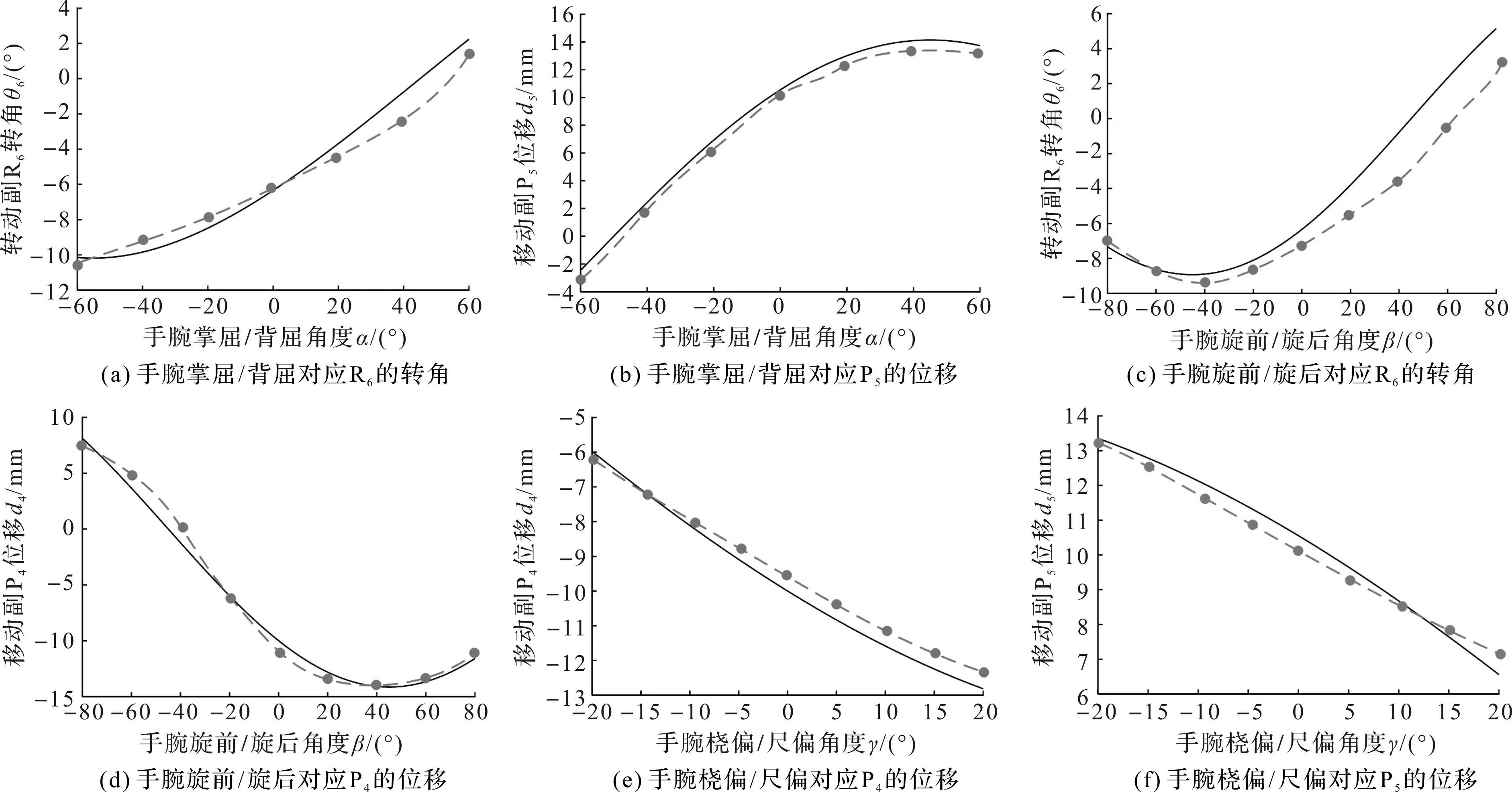
图7 被动副运动曲线图实线——约束方程解出曲线；虚线——康复平台仿真曲线

由图7(a，c)可知：θ6随角度α与β的增大基本呈现上升趋势，但在-80°<β<-40°时略有下降，且在起始点(α、β与γ角度都为0°的点)θ6的值约为-6.5°；

由图7(b，f)可知：d5随角度α增大而增加，随角度γ增大而减小，且它的正向运动位移远大于负向运动位移；

由图7(d，e)可知：d4随角度β与γ的增大基本呈现下降趋势，但在40°<β<80°时略有上升，正向运动位移与负向运动位移相差不大；

由图7可知：在进行内旋/外旋、掌屈/背屈与桡偏/尺偏3种康复运动时，3个被动副均呈现平滑、无突变连续运动，表明该机构构型在康复运动时无力与力矩的突变，满足腕关节康复训练时的受力条件；

根据图7，并结合逆解析计算出的固定值可知：θ6的运动范围(-11°～6°)，d4运动范围(-15 mm～ 8.5 mm)，d5的运动范围(-2.5 mm～15 mm)。由此可见：3个被动运动副运动幅度均较大，表明增加的3个被动副在缓解运动不相容问题方面具有现实意义；进一步，通过分析逆向求解过程可知，可通过设定一定范围的人机穿戴偏差，对运动约束方程求逆解来确定被动机构运动范围，该结果可为后续机器人结构设计提供必要的数据支撑；

最后，通过对比图7中仿真曲线(虚线)与对约束方程的计算曲线(实线)可知：仿真曲线与对约束方程的计算曲线运动趋势基本相同，且均较为顺滑；同一瞬间各被动副运动的位移与角度偏差相差不大。以上结果可以验证，所建立的机构约束方程与设计的三维模型是正确的。

4 结束语

(1)笔者提出了一种3RPPR型自调节式手腕康复外骨骼机构，该机构可实现手腕内旋/外旋、掌屈/背屈与桡偏/尺偏3种独立康复运动方式；

(2)通过引入与人机接触面相连的被动副，解决了人体腕关节与康复机构各关节中心不匹配的问题；并通过各被动副运动幅度均较大且连续平滑、无突变的特点，验证了该机构构型可有效缓解由于人机偏差引起的沿人体轴向的力与绕人体轴向的力矩；

(3)通过人机闭链运动学分析，建立了运动学约束方程，并对约束方程求逆解，确定了被动机构运动范围，该结果可为后续康复机器人结构设计提供数据支撑。