弹性隔套轴向受压仿真与参数优化研究*

徐行胜，周 旭，伍 英

(湖北汽车工业学院 机械工程学院，湖北 十堰 442002)

0 引 言

弹性隔套是轮毂单元的重要零件，对轮毂单元的轴承预紧[1，2]有着非常重要的作用。轮毂单元在工作到一定的时间后，弹性隔套及轴承会有一定的磨损，而弹性隔套则会有一定的回弹量，以确保轴承预紧力在合适的预紧范围内。

当前，已有多位学者对弹性隔套进行了不同领域的研究。文献[3]对驱动桥主动锥齿轮轴承的预紧参数进行了计算和分析，对弹性隔套的受力与变形曲线进行了分析研究；文献[4]结合弹性隔套的设计要求和力学性能准则对弹性隔套进行了理论分析，并利用有限元分析软件ABAQUS对弹性隔套进行了弹塑性仿真分析，研究得出了考虑塑性加工的弹性隔套弹性刚度与试验结果更接近。文献[5]利用有限元方法对弹性隔套进行了仿真分析，并对弹性隔套的载荷和回弹量进行了设计,评估了弹性隔套的支持刚度；文献[6-9]对弹性隔套的复合缩径-胀形进行了试验研究，对弹性隔套进行了应力场的求解，并计算出了弹性隔套特性曲线的理论解，而且初步探索了弹性隔套结构参数对轴向力的影响；文献[10-12]通过设计试验和轴向压缩有限元仿真的方法，分析了弹性隔套的结构参数对弹性隔套特性曲线的影响，并通过构建响应面模型，利用优化算法对弹性隔套最佳工作段长度进行了优化，研究得出了利用响应面代替有限元法分析的结果是可靠的。

总体而言，笔者对弹性隔套特性曲线和性能以及设计方面已进行了大量研究；在此基础上，笔者基于弹性隔套的实际应用及结构的多样性，通过某轮毂单元中弹性隔套样品，对弹性隔套进行压缩实验，并对弹性隔套进行多目标优化设计。

1 弹性隔套有限元仿真与压缩实验

弹性隔套的几何形状多种多样，根据实际工程中的应用，由某厂家提供隔套样本，本文研究其轮端总成中的弹性隔套。

弹性隔套的结构如图1所示。

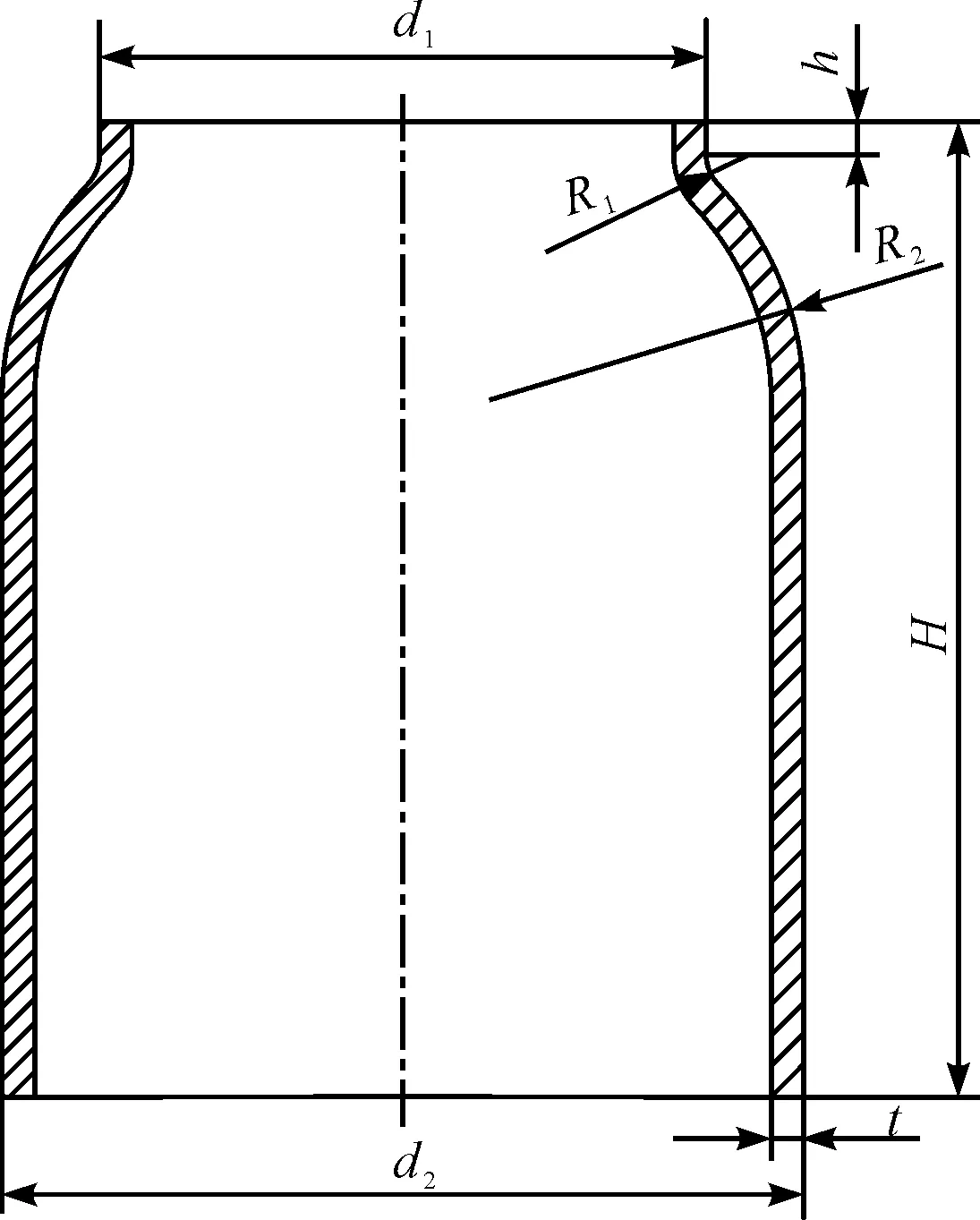
图1 弹性隔套的结构t-壁厚；R1-小端过渡圆弧半径；R2-大端过渡圆弧半径；d1-小端直径；d2-大端直径；h-小端直壁长度；H-轴向总高度

图1的弹性隔套结构中，上下两端为直壁部分，中间为两段过渡圆弧连接上下直壁部分。实际提供的样品在过渡圆弧处壁厚与整体壁厚不等，本文在研究时看作壁厚均匀一致。

1.1 特性曲线与应力有限元仿真

笔者利用有限元软件ABAQUS对弹性隔套进行数值模拟仿真，根据弹性隔套的工作状况，模拟弹性隔套在上下刚体压头作用下的压缩过程，并得到了弹性隔套在受压过程中的轴向力与压缩量曲线。

仿真采用各向同性材料，弹性模量E=35 GPa，泊松比为μ=0.26，仿真采用四节点轴对称单元模型。

弹性隔套的有限元模型如图2所示。

图2 弹性隔套的有限元模型

在图2弹性隔套的有限元模型中，上下两端为轴对称解析刚体，中间为弹性隔套，使下解析刚体固定不动，上解析刚体向下压缩0.4 mm。

仿真得到弹性隔套在受压过程中的轴向力与压缩量特性曲线如图3所示。

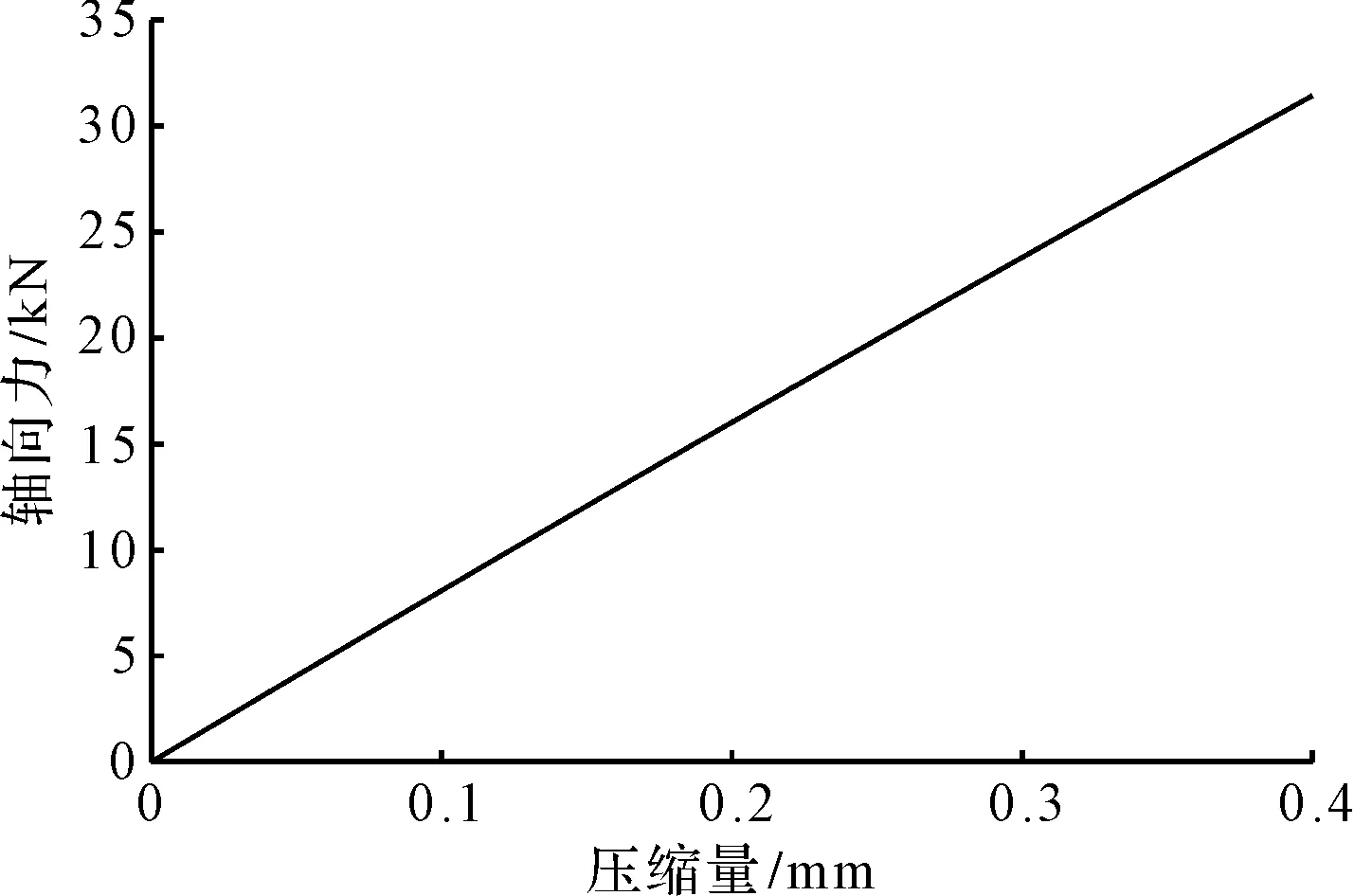
图3 轴向力与压缩量特性曲线

由图3可以看出：弹性隔套在轴向受压过程中轴向力与压缩量呈线性变化，其斜率大小反映出了轴向力大小变化趋势的快慢；工程根据实际情况需要对其进行调整以保证隔套在工作磨损后有一定的回弹量，具有一定的预紧补偿作用，确保轮毂轴承的合适预紧，使轴承寿命得到保障。

弹性隔套的mises应力云图如图4所示。

图4 弹性隔套的mises应力云图

从图4弹性隔套的mises应力云图可以看出，弹性隔套的最大应力出现在小端过渡圆弧上，此处遭受破坏的可能性最大。

1.2 弹性隔套的压缩实验

根据某厂提供的样品，笔者对其中的两个弹性隔套进行压缩实验，压缩实验在某拉伸压缩试验机上进行，压缩实验如图5所示。

图5 压缩实验

图5中，试验机的下端压头固定在底座上，上压头由试验机的加载往下运动对弹性隔套进行压缩，试验机可以输出压头的位移和力的数据，与前述有限元仿真得到的弹性隔套的轴向力与压缩量特性曲线进行对比。

实验与有限元轴向力压缩量曲线如图6所示。

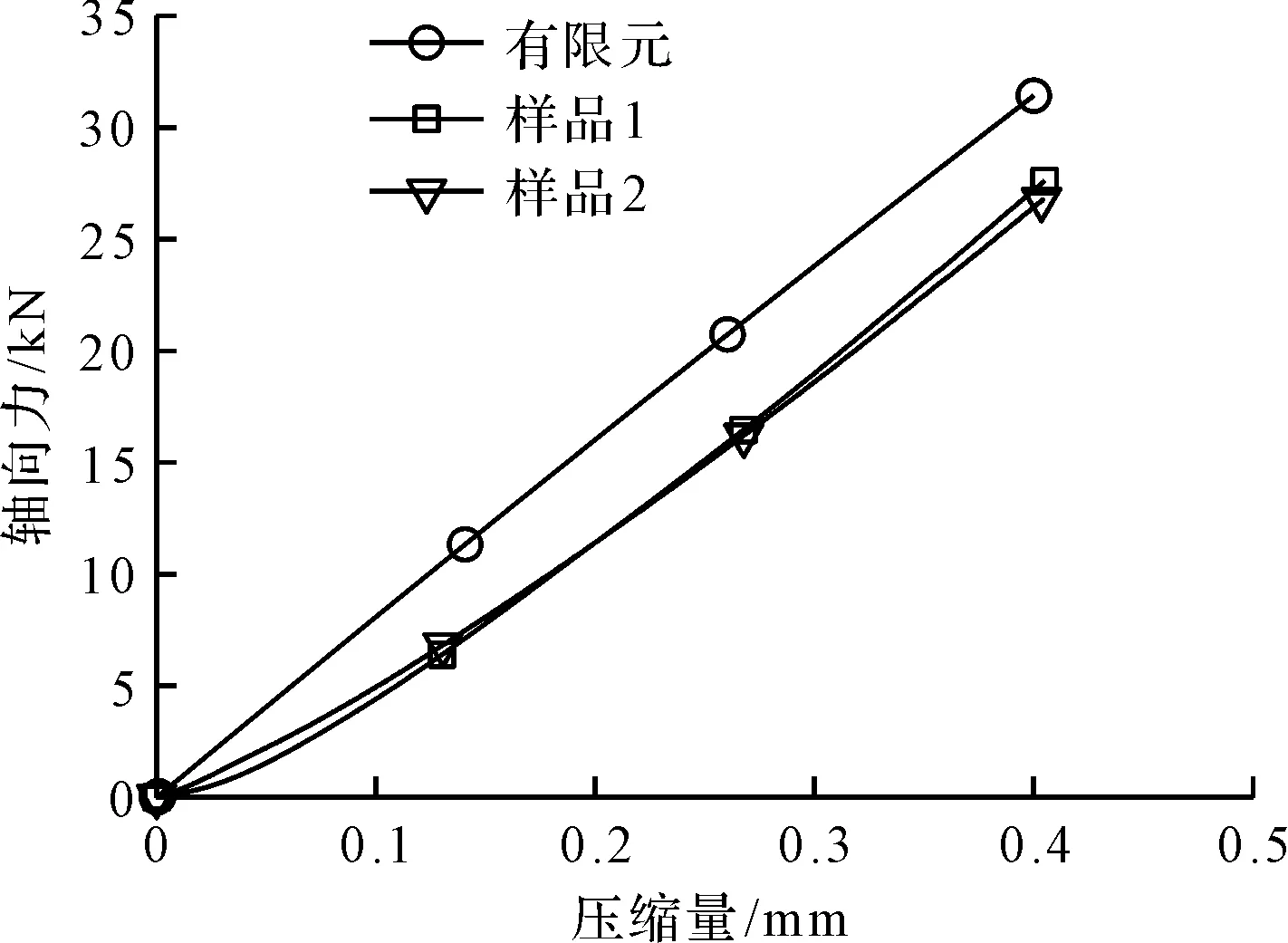
图6 实验与有限元轴向力压缩量曲线

从图6实验与有限元轴向力压缩量曲线可以看出：样品1和样品2形状相似，由于加工和实验的误差两者的特性曲线稍有偏差，有限元仿真的弹性隔套几何形状壁厚等与样品隔套的壁厚稍有差异，且实验有实验误差，有限元仿真的特性曲线与实验也有偏差。

总体而言，特性曲线的斜率相近，轴向力变化趋势相同，有限元仿真与实验的特性曲线具有较好的一致性。

2 优化设计

2.1 正交试验组的建立

正交试验设计是用于多因素试验的一种方法，利用正交试验点具有均匀整齐的特点，可从全面试验中挑选出部分具有代表性的试验点进行试验，以减少试验的次数。

弹性隔套的设计参数有4个，每个参数取4个水平，为了保证试验的精度，采用L64(421)正交表，任取其中4作为试验设计表，一共64组试验。

每个水平下，各参数因子水平如表1所示。

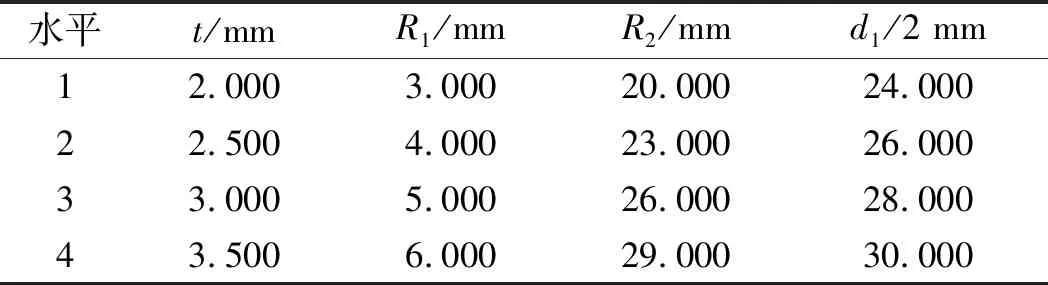
表1 各参数因子水平

笔者利用组合优化软件Isight，对弹性隔套进行了正交试验，可得到各个因素对特性曲线斜率与最大mises应力的主效应图。

各因素对特性曲线斜率与最大mises应力的主效应图如图7所示。

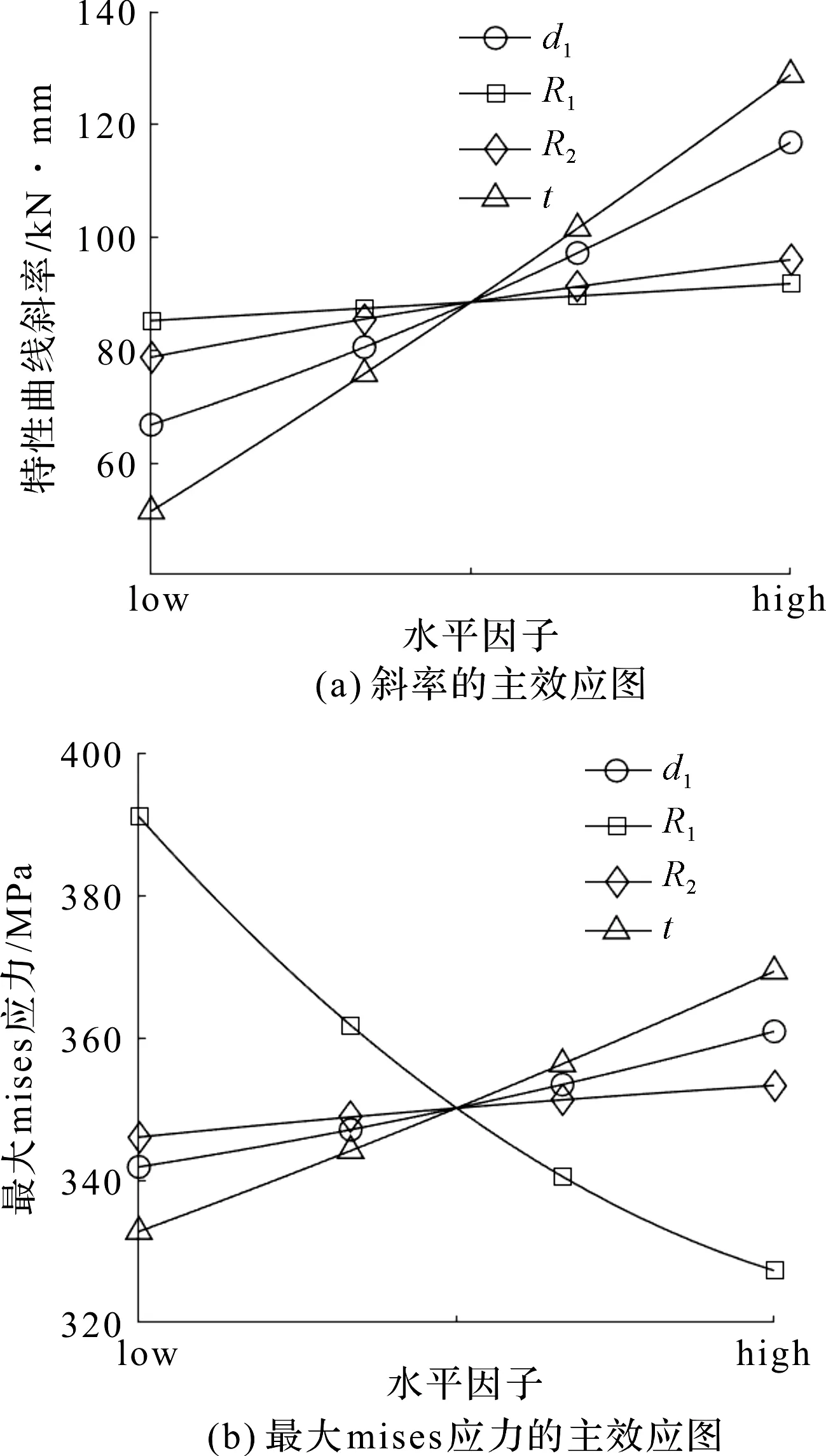
图7 特性曲线斜率与最大mises应力的主效应图

由图7可以看出：特性曲线斜率受t和d1的影响较大，且都随两者的增大而增大，受R2和t的影响较小；最大mises应力受t和d1的影响较大，但是两者变化的方向不同。

2.2 特性曲线斜率与最大mises应力响应面模型

为了减少弹性隔套结构在有限元优化计算的时间，笔者采用响应面法来代替有限元，采用二阶响应面模型，为后续的多目标优化做准备。

二阶响应面模型如下：

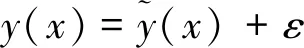
(1)

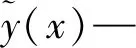
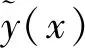
(2)

利用Isight软件可以对特性曲线的斜率和最大mises应力进行拟合，得到各自的响应面。

拟合得到特性曲线斜率的各系数值为：C0=139.180,Ci=[-177.912,6.773,6.365,-69.485],C4+i=[0.365,0.001,-0.557,2.902],Cij=[-0.154,-0.096,3.434,-0.066,0.422,0.426]。

拟合得到最大mises应力的各系数值为：C0=-130.820,Ci=[11.850,-18.812,17.144,83.535],C4+i=[0.140,4.020,-0.022,1.667],Cij=[-0.614,-0.475,-0.663,-0.091,-0.7.208,-0.735]。

特性曲线的斜率与最大mises应力的拟合精度R2为1.000和0.998，均在0.99以上，响应与样本非常接近，能够很好地代替有限元，为弹性隔套结构参数的优化做准备。

2.3 弹性隔套多目标优化

多目标优化问题是指多个目标函数不能同时达到最优解的问题，其优化结果一般为一个解集，称为Pareto最优解集。

根据实际工程中的应用，弹性隔套的特性曲线斜率应尽可能小，以增大弹性隔套轴向力的控制调节范围；弹性隔套在受压过程中最大mises应力应尽可能的小，以免弹性隔套发生破坏。

由图7可知，两者不能同时达到；笔者采用第二代非劣遗传算法(NSGA-II)求解弹性隔套的Pareto解集；利用组合优化软件Isight实现NSGA-II算法，对弹性隔套进行多目标优化。

笔者取种群规模为100，种群迭代数为50，交叉率为0.9。

设置弹性隔套的设计变量上下限如表2所示。

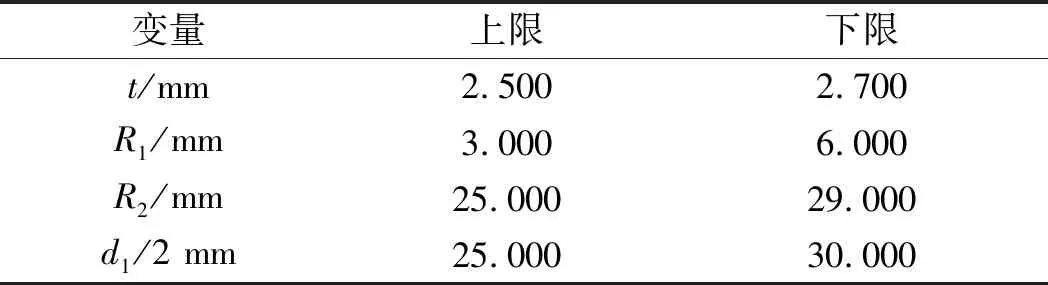
表2 设计变量的取值范围

3 优化结果及分析

笔者利用组合优化软件Isight实现NSGA-II算法，对弹性隔套结构进行多目标优化，得到弹性隔套的Pareto前端如图8所示。

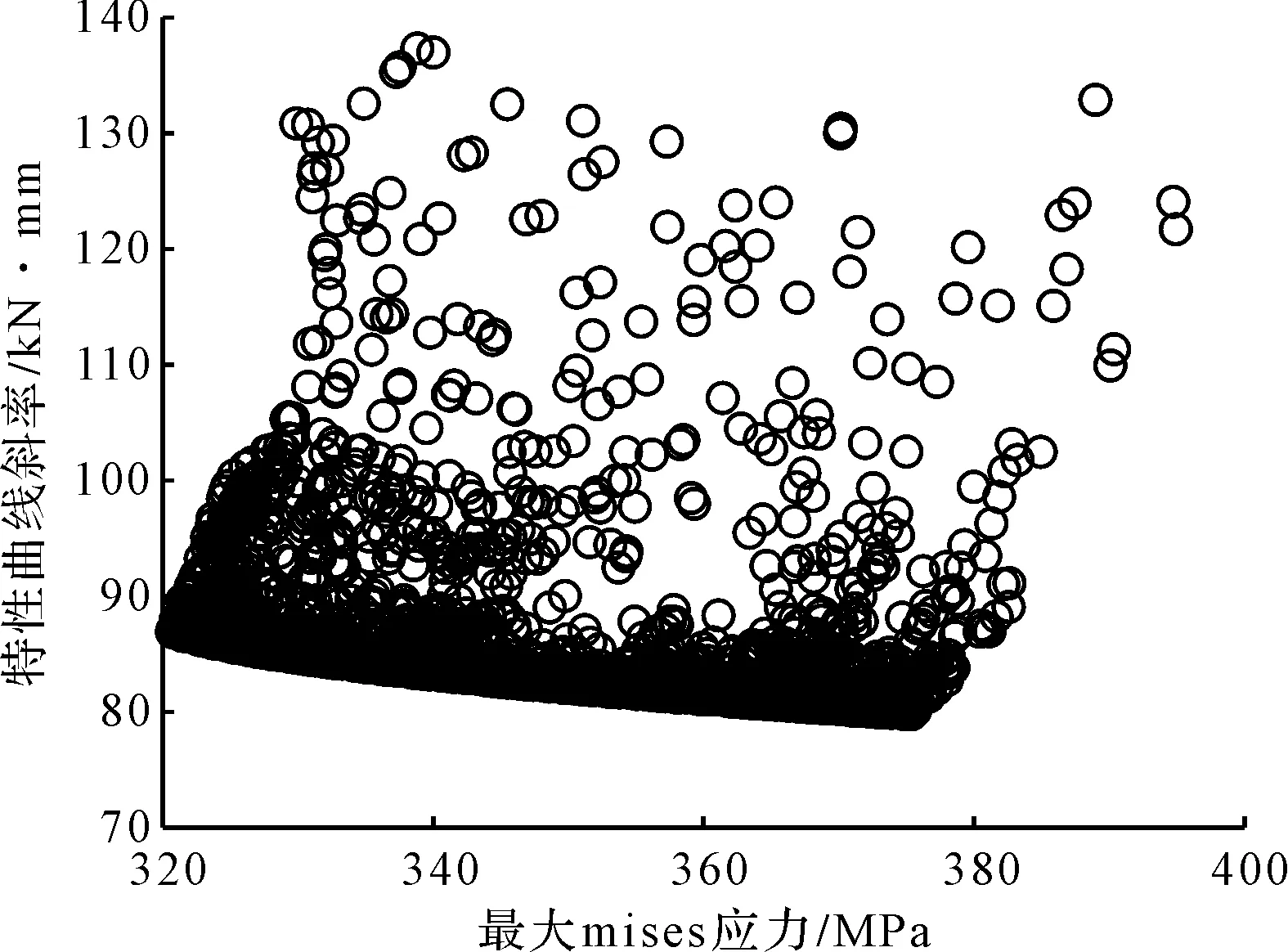
图8 弹性隔套的Pareto前端

在实际工程生产过程中，应根据需要，对特性曲线斜率与最大mises应力这两个目标中进行舍取，从Pareto最优解集中取一组作为设计参数。

部分Pareto最优解如表3所示。

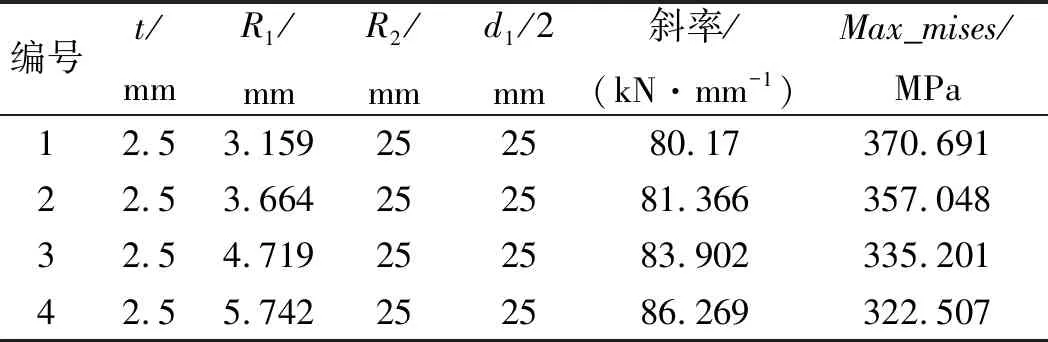
表3 部分Pareto最优解

笔者将多目标优化所得到的部分Pareto最优解代入到ABAQUS软件进行计算，计算出各自的特性曲线斜率与最大mises应力；将用有限元法计算得到的结果与用响应面计算得到的结果进行对比，有限元与响应面对比如表4所示。

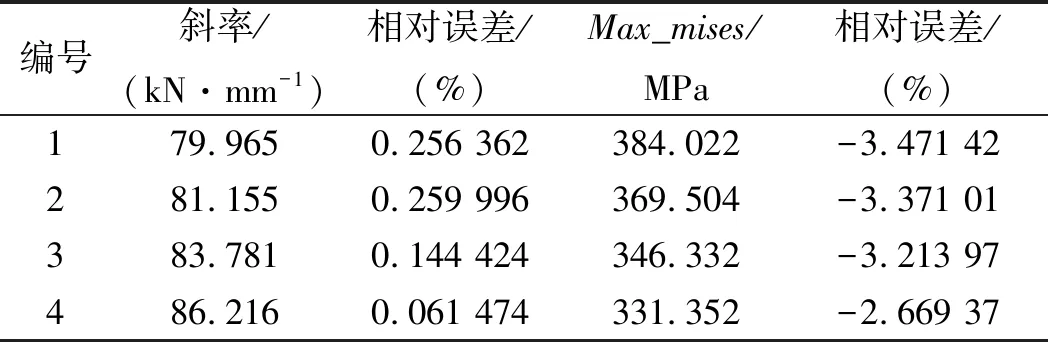
表4 有限元与响应面对比

由表4可以看出：用响应面得到特性曲线斜率和最大mises应力与有限元计算得到的结果相对误差均在4%以下，说明响应面模型计算出来的结果代替有限元计算出来的结果具有较高精度，利用多目标优化得到的弹性隔套的几何参数是可靠的。

4 结束语

本研究通过对某轮端总成的弹性隔套进行轴向压缩有限元仿真和压缩实验，分析了弹性隔套在轴向受压过程中应力和轴向力与压缩量特性曲线的变化规律；利用正交试验分析了弹性隔套结构参数对特性曲线斜率和最大mises应力的影响，并且构造了特性曲线斜率和最大mises应力的响应面模型；结合Isight组合优化软件，利用多目标优化算法NSGA-II对弹性隔套进行了优化。

研究结果表明：优化后的斜率和最大mises应力响应与有限元计算结果的相对误差均在4%以下，表明构造的响应面模型能够近似代替有限元法对隔套进行分析，这为在实际工程中弹性隔套的结构参数优化设计提供了参考。

随着弹性隔套的形状与材料的日趋多样化，笔者对弹性隔套特性曲线及性能以及结构参数设计仍要做进一步研究。