陡波形立管涡激振动疲劳损伤参数敏感性分析❋

顾洪禄，郭海燕，刘 震

(中国海洋大学工程学院，山东 青岛 266100)

近年来，钢悬链线立管由于具有良好的技术优势和商业前景，在深海油气行业得到了广泛的应用，并逐渐成为深海油气开发首选立管形式[1]。在各种形式的钢悬链线立管中，陡波形立管通过在中间管段设置一定数量的浮块形成拱弯段大幅度降低了顶部悬挂点的有效张力，进一步提高立管服役期间的疲劳寿命。除此之外，陡波形立管具有陡峭的构型，立管触地段与海底夹角接近90°，因此可以有效避免海床管线稳定性问题，特别适用于管内流体密度发生变化的立管[2]。

立管在运行期间会受到海流的影响，一定流速的海流会引起立管两侧产生交替的漩涡脱落，立管在漩涡脱落作用下产生周期性的振动，称之为涡激振动[3]。涡激振动会导致立管疲劳损伤，当涡脱频率接近立管固有频率时会发生“锁定”现象，此时立管振动将会控制漩涡脱落并会伴随有更强烈的振动和更大的振幅，这将会加剧立管的疲劳损伤[4]。立管的疲劳破坏会导致严重的油气泄漏以及大范围的海洋环境污染，因此对于深海立管涡激振动导致的疲劳损伤问题进行深入研究具有重要意义。

关于立管的涡激振动疲劳损伤，国内外学者进行了大量的研究：Baarholm等[5]通过分析观察Hanøytangen试验，发现顺流向的振幅较小但频率较高，顺流向与横流向对于立管的疲劳损伤几乎相同；Sun等[6]利用虚拟激励法对深水立管在剪切流作用下的涡激振动响应进行了数值研究，对立管的涡激振动疲劳寿命进行了分析研究；Wang等[7]提出了一种考虑土体相互作用的VIV预测模型，用于预测钢悬链线立管触地点疲劳损伤，并利用该模型对钢悬链线立管触地点疲劳寿命进行了参数敏感性分析；高云等[8]在拖曳水池中对柔性立管的涡激振动响应进行了试验研究，并分别使用频域法以及雨流法对疲劳损伤进行分析；秦伟等[9]采用点涡强度计算流体对结构的横流向和顺流向脉动水作用力，推导出的双向涡致疲劳分析对结构的疲劳损伤评估更为全面；郭海燕等[10-11]对立管在内外流体、顶部张力共同作用下的涡激振动疲劳问题进行了数值分析和试验研究。目前关于陡波形立管涡激振动疲劳损伤的研究鲜有报道。

在细长柔性立管涡激振动研究中，大部分认为横向涡激振动响应幅值远大于顺流向，但顺流向频率较高。目前，国际工程界广泛认可的涡激振动预报程序SHEAR7[12]、VIVANA[13]、VIVA[14]也都只关注了立管横流向涡激振动响应，因此本文没有关注顺流向的涡激振动响应，只考虑陡波形立管的横流向涡激振动响应。

本文基于柔性杆理论和尾流振子模型计算陡波形立管的涡激振动响应；综合使用S-N曲线法、雨流计数法[15]与Palmgren-Miner线性累积损伤理论，对陡波形立管进行疲劳损伤分析。以MATLAB为平台编写陡波形立管涡激振动疲劳损伤计算程序。把本文程序得到的静力计算结果以及立管的前五阶固有频率与商业软件OrcaFlex计算结果进行对比，并将本文计算的疲劳损伤与已发表文献进行对比，验证了模型的正确性，进而对陡波形立管在不同浮子段长度、浮力因子、弹性模量、海流速度、波浪高度下的涡激振动疲劳损伤进行参数敏感性分析。

1 1 数值计算模型

1.1 柔性杆模型

柔性杆模型[16]在全局坐标系下直接得到包含全部几何非线性的控制方程，避免了繁琐的坐标系变换。如图1所示，在三维笛卡尔坐标系中，杆的位形由杆轴线位置表示，利用弧长与时间的函数代表的空间曲线r(s,t)来描述变形后柔性杆的轴线位置状态[17]。

假设变形前后杆的弧长不发生改变；作用于轴线上的合力F与力矩M可以完全表示立管任一点的内力状态；忽略转动惯量和剪切变形的影响、均布扭矩和分布外力矩的作用；假定立管可伸长并且伸长量为小量。

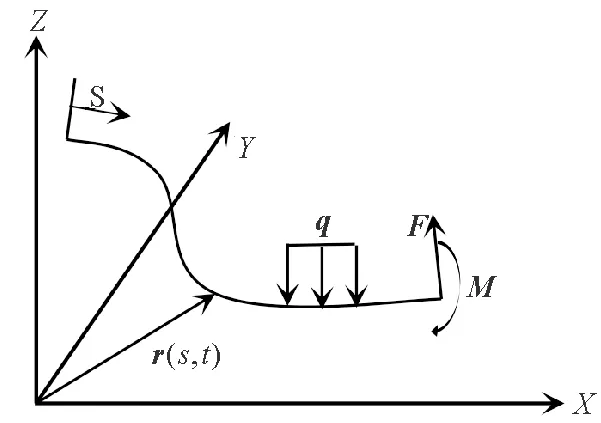
图1 柔性杆坐标系示意图Fig.1 Diagram of slender rods

在柔性杆模型下得到立管的运动方程以及变形条件如下[18]：

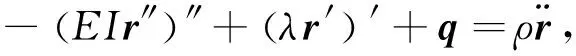
(1)

(2)

式中ρ是单位长度质量；q是单位长度分布外力；λ=λ(s,t)是标量函数。

将柔性杆控制方程和变形条件分别写成张量形式，利用三次Hermit插值函数进行离散，运用Galerkin方法得到矩阵形式的微分方程如下:

(3)

(4)

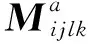
设公式(3)的解为

(5)

[H]{Z}=λ{Z}。

(6)

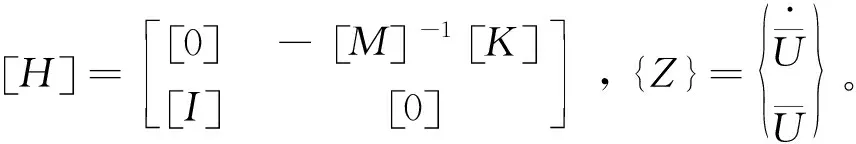
1.2 涡激振动响应计算

本文采用Matteo Luca Facchinetti[19]推荐的尾流振子模型，该模型振动方程如下：

(7)

(8)

式中:qx是立管无量纲尾流振子变量；ωs为漩涡脱落频率，由于陡波形立管并非垂直于来流方向，式(8)中速度采用沿立管单元法向的流速分量，并且此处考虑立管运动与外部流体之间的相对速度；εx为由试验确定的无量纲参数；Ax为由试验确定的横向流体动力参数。

同样采用三次Hermit插值函数对尾流振子模型进行离散得到矩阵形式的单元运动方程如下:

(9)

将立管单元涡激振动耦合振动方程组(3)、(4)、(9)分别整合获得整体耦合方程组的矩阵表达形式：

(10)

(11)

(12)

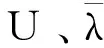
(13)

本文对图2所示陡波形立管的下降段，浮子段，悬垂段涡激振动响应进行分段计算，对装配有浮块的浮子段，本文按照单位长度体积、质量不变原则将其等效为具有均匀直径的管段，等效直径、等效质量分别为[20]：

(14)

(15)

式中：Dp是立管外径；Df是浮块外径；Lf是浮块长度；Sf是浮块节距；Mp是立管单位长度质量；ρf是浮块密度；Mfh是附属质量。

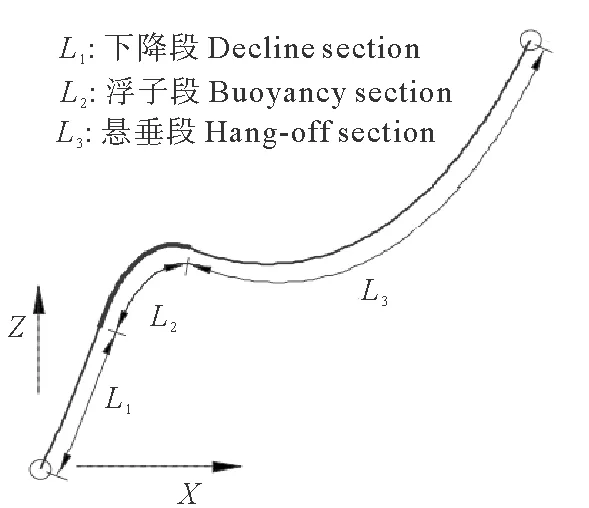
图2 陡波形立管Fig.2 Steep-wave riser

1.3 疲劳损伤分析

通过雨流计数法，得到应力范围、应力均值和应力范围出现的次数。再根据等效损伤原则，选用如下Goodman经验公式，将非零应力均值的应力范围转换成零应力均值的应力范围：

(16)

式中：S表示等效零均值应力；Sai表示第i个应力幅值；Smj表示第j个应力均值；σb表示材料的强度极限。

对于恒定的应力范围，失效的应力循环次数可以由S-N曲线表示为：

logN=loga-mlogS。

(17)

式中：S表示应力幅值；a,m是由试验确定的经验系数。

根据Palmgren-Miner线性累积损伤理论，并参考规范DNV RP-C203[21]，立管整体疲劳设计需要满足以下公式：

(18)

(19)

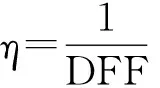
利用MATLAB平台，将式(10)～(19)编写成相应程序计算陡波形立管在涡激振动下的疲劳损伤。

2 疲劳损伤参数敏感性分析

2.1 模型验证

选取参考文献[23]的立管参数：水深1 200 m，立管顶部偏移1 300 m，立管总长2 200 m，下降段300 m，浮子段600 m，悬垂段1 300 m，内径0.3 m，下降段、悬垂段外径为0.35 m，浮子段等效外径为0.85 m，轴向刚度5×106N，抗弯刚度6.3×107N·m2，材料密度7 860 kg/m3，浮力因子n=2。均匀海流速度v=0.85 m/s，海流沿X方向，参照DNV-RP-C203(2008)[21]，选取海水环境中没有阴极保护下的S-N曲线中的D曲线，loga=11.687，m=3，该立管材料的强度极限σb=1 134 MPa。

将本文程序计算得到的静力分析结果及前五阶固有频率与商业软件OrcaFlex计算结果进行对比，如图3～6所示，从图中可以看出，两者计算结果吻合良好，从结构层面证明了本文模型的正确性。

为进一步验证本文整体模型的有效性，利用本文模型对文献[24]中悬链线立管进行建模，并计算其环流作用下的疲劳损伤，并与文献中SHEAR7的计算结果进行对比，文献中具体参数如下：水深1 500 m，立管总长1 675 m，外径0.355 6 m，内径0.320 6 m，顶部偏移800 m，垂直距离1 356 m，弹性模量E=2.07×105MPa，内部流体密度865 kg/m3，流速分布与对比结果如图7～8所示：

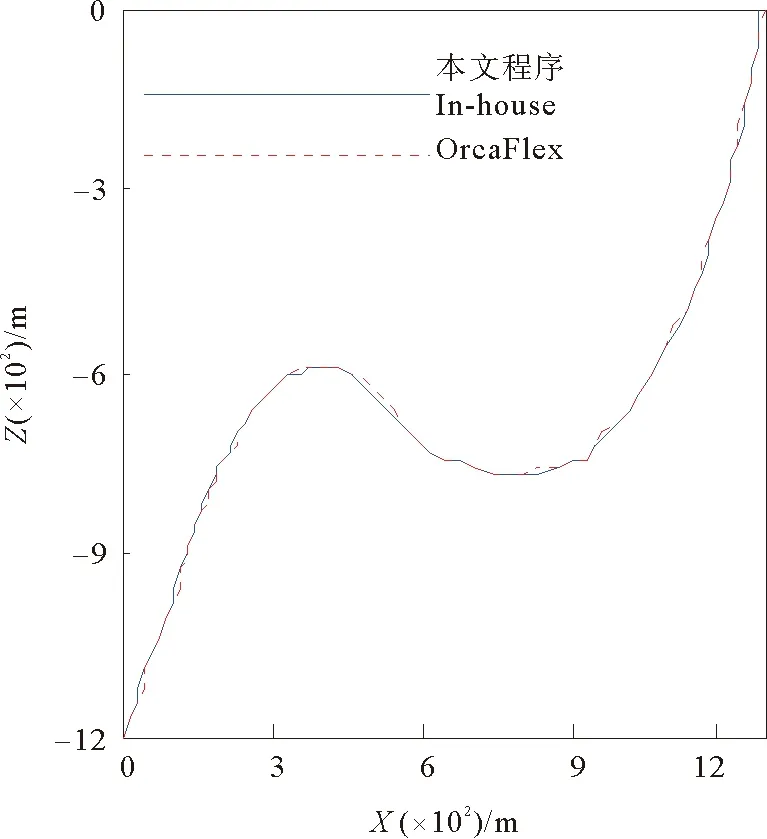
图3 静力位形对比Fig.3 Comparison of static configuration

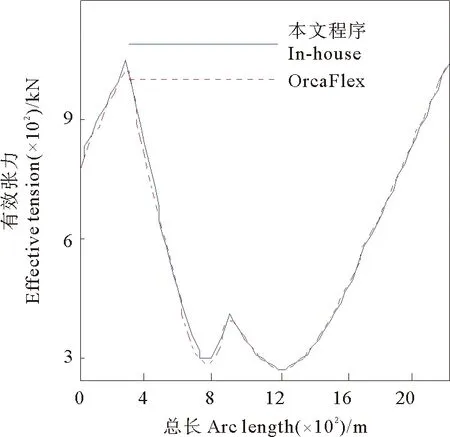
图4 有效张力对比

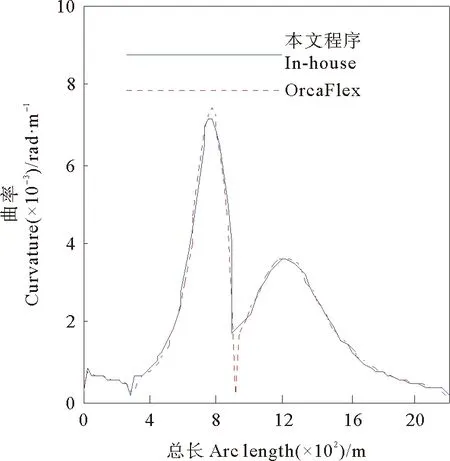
图5 曲率对比

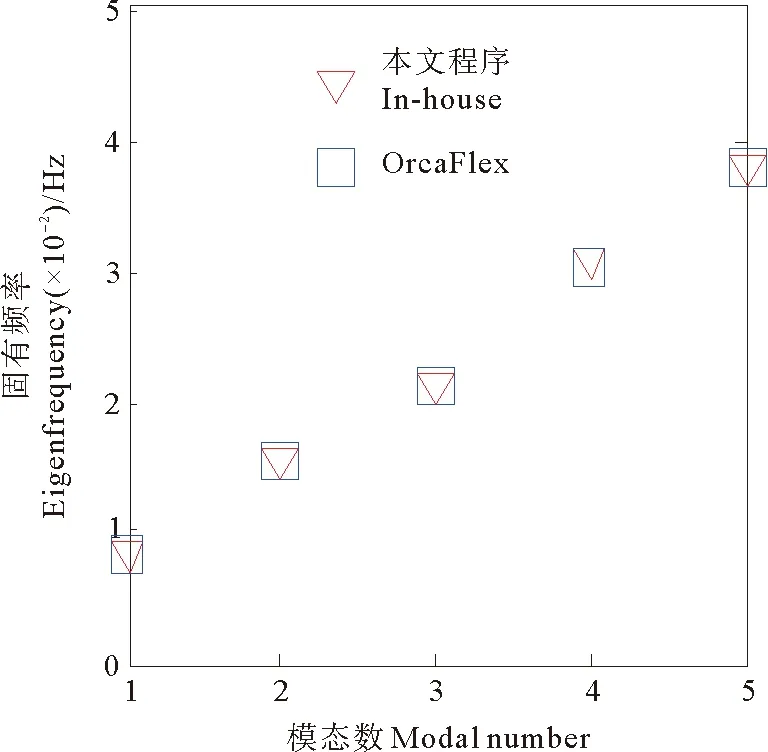
图6 固有频率对比

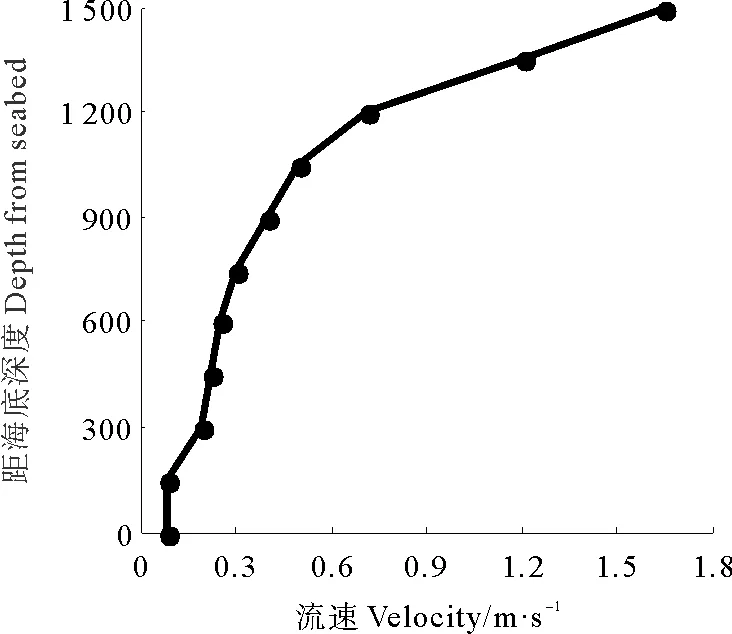
图7 流速分布Fig.7 Current velocity profiles

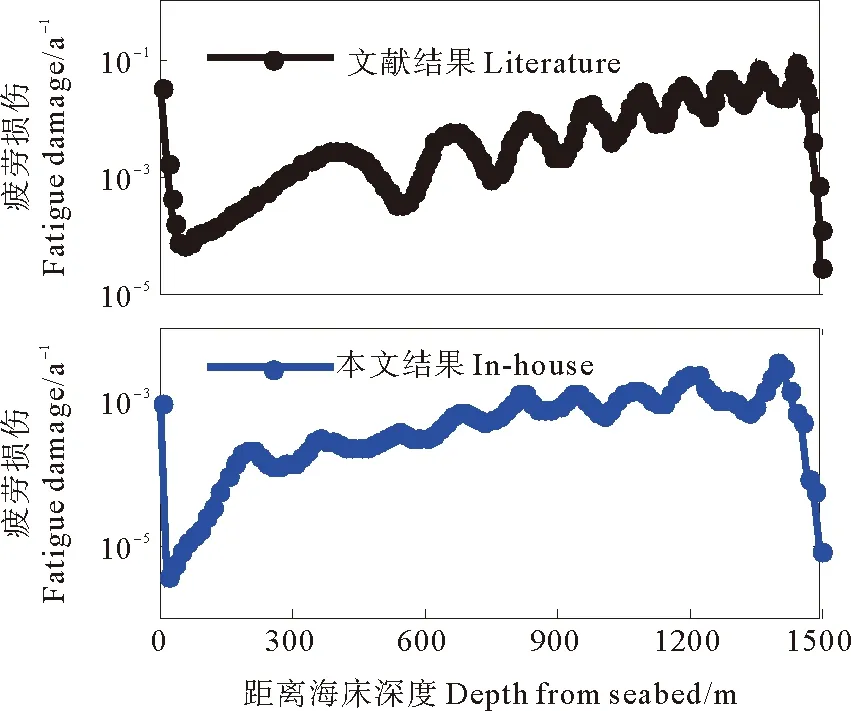
图8 疲劳损伤对比Fig.8 Comparison of fatigue damage

如图8所示，本文计算结果与文献结果有一定的差异，这主要是由于SHEAR7是利用模态叠加法在频域内对涡激振动响应进行计算，而本文是在时域内进行计算，且计算方法也与之不同；除此之外，Chaplin等[25]对各种柔性立管涡激振动的计算模型进行了比较，结果显示各个模型预测结果相差较大，并且与实验结果有较大的差距。

但也可以看出本文计算的疲劳损伤在数值上与文献结果相差不大，并且两者计算结果的变化趋势与模态数一致。因此一定程度上验证了本文模型的整体有效性。

2.2 浮子段长度参数敏感性分析

下降段长度及其他参数保持不变，当浮子段长度L2=550、600、650 m时，分别计算立管的涡激振动响应下的疲劳损伤，计算结果如图9及表1所示。

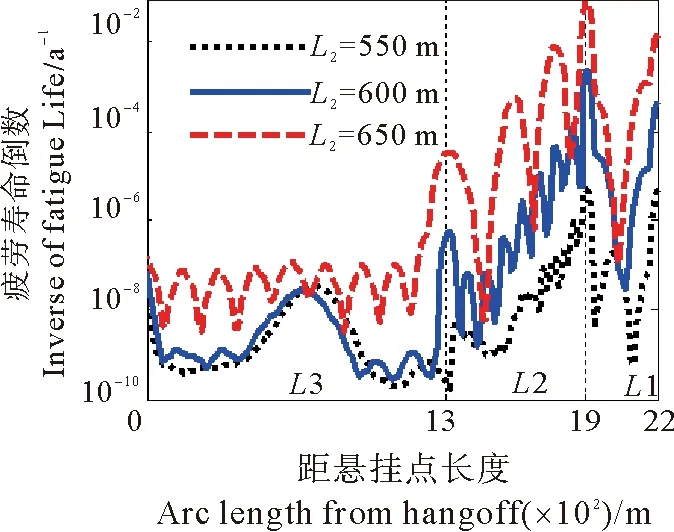
图9 不同浮子段长度立管疲劳损伤对比Fig.9 Comparison of fatigue damage of riser with different float segment lengths

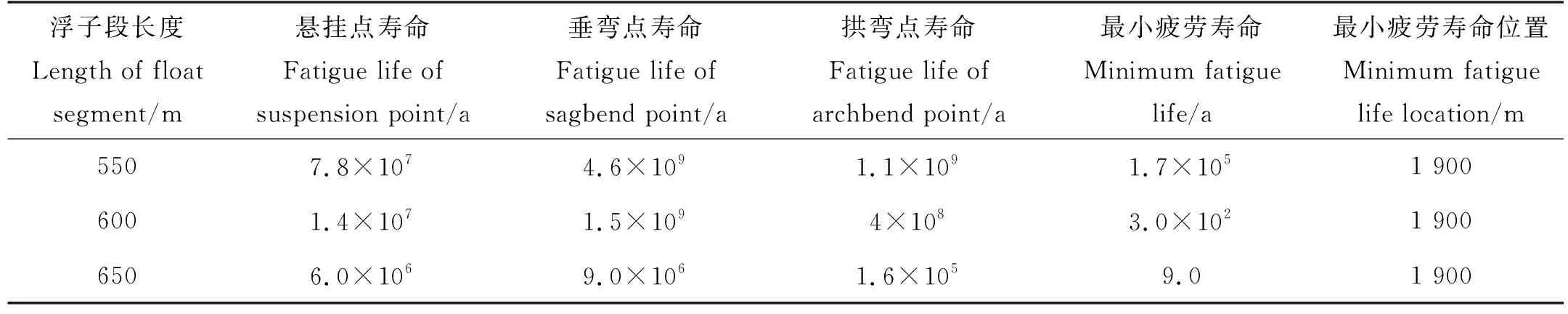
表1 不同浮子段长度立管疲劳寿命Table 1 Fatigue life of riser with different float segment lengths

从图9中可以看出，立管整体对浮子段长度的变化较为敏感，立管的疲劳损伤沿轴线方向呈振荡性质，这与文献[4，26]中对具有大长细比的柔性管的涡激振动疲劳分析结果相同。

计算结果表明：随着浮子段长度的增加，立管的疲劳损伤呈现上升的趋势，因此在通过增加浮子段长度降低悬挂点张力的同时，应考虑该参数对于立管整体疲劳损伤的影响；随着浮子段长度的增加，悬垂段激发的模态数增加，浮子段激发的模态数减少，并且浮子段疲劳损伤程度高于悬垂段和下降段。

在浮子段首末两端以及触地点疲劳损伤急剧升高，这是由于截面的突然变化产生应力集中现象，进而导致疲劳损伤的急剧增大，因此实际工程中应对浮子段首末两端和触地点采取恰当的抑振措施；除此之外，浮子段末端与触地点由于浮子段提供的浮力导致两点轴向应力循环水平较高，致使疲劳损伤高于其他节点。

由表1可以看出，在相同参数下，最小疲劳寿命点始终位于浮子段末端，最小疲劳寿命随浮子段长度的增大急剧下降；由此可见该参数是影响陡波形立管疲劳损伤的关键因素。

2.3 浮力因子的参数敏感性分析

浮力因子n=-Wf/W，其中，W为下降段、悬垂段立管单位长度的湿重，Wf为浮子段部分立管单位长度的湿重。

保持其他参数不变，当浮力因子n=1.5、2.0、2.5时，分别计算立管的涡激振动响应下的疲劳损伤。计算结果如图10及表2所示。

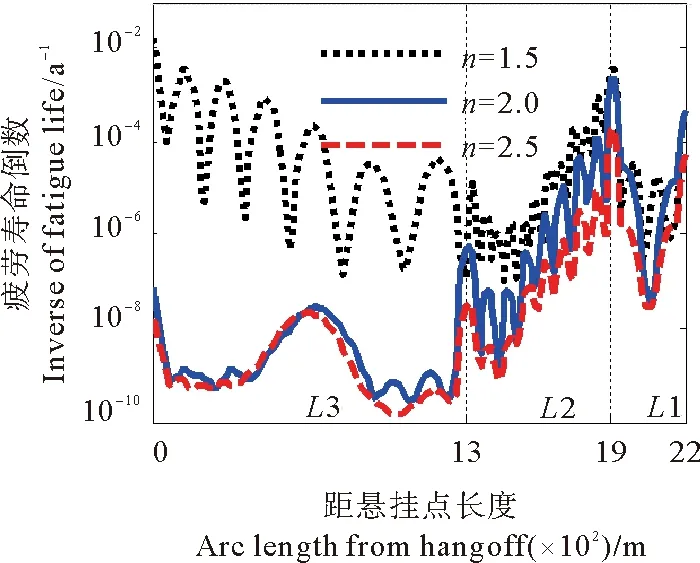
图10 不同浮力因子立管疲劳损伤对比Fig.10 Comparison of fatigue damage of riser with different buoyancy factors

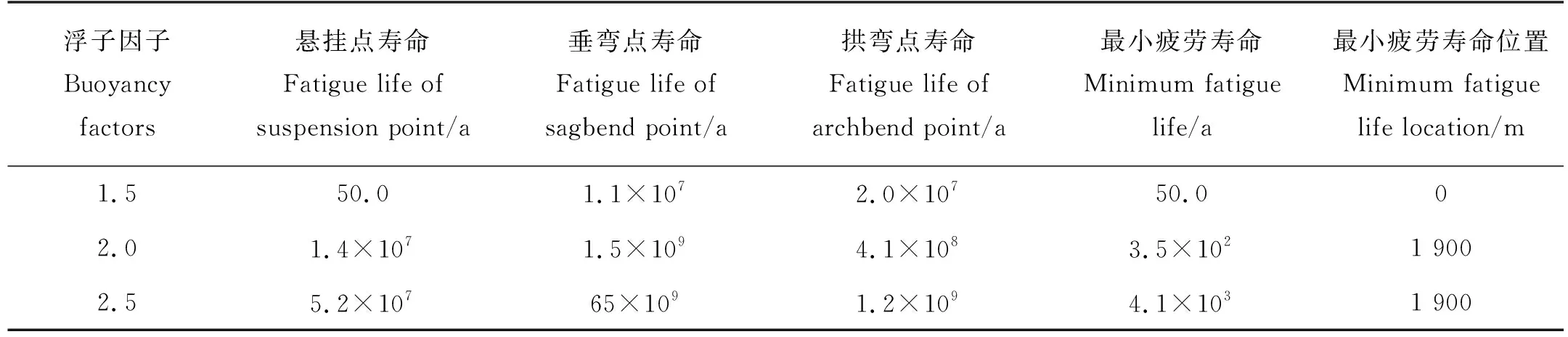
表2 不同浮力因子立管疲劳寿命Table 2 Fatigue life of riser with different buoyancy factors

由图10可以看出，浮力因子对于陡波形立管整体疲劳损伤的影响较大，随浮力因子的增大，疲劳损伤整体出现下降趋势；相比于浮子段与下降段，悬垂段对于浮力因子的变化最为敏感，主要因为悬垂段低模态响应为主，在低模态下立管本征频率主要由张力控制，而浮力因子会直接影响悬垂段张力的大小，因此悬垂段对该参数较为敏感；低浮力因子下悬垂段疲劳损伤最高，高浮力因子下浮子段疲劳损伤最高，主要因为低浮力因子下悬垂段张力大、激发的模态数多，导致了该端处于较高的轴向应力与弯曲应力循环水平。

由表2可以看出，随着浮力因子的增大，最小疲劳寿命升高，最小疲劳寿命点由悬挂点转移至浮子段末端，是因为浮力的增加降低了悬挂点处的应力循环水平。因此增加浮力因子不仅可以有效降低悬垂段的张力而且能较大程度降低悬垂段疲劳损伤。

2.4 弹性模量的参数敏感性分析

近年来，立管制造业中涌现出了铝合金、复合材料等多种立管材料，并对相关材料进行了研究[27-28]。本文对材料的重要属性-弹性模量进行参数敏感性分析，希望能够提供一定参考。

保持立管其他参数不变，当立管材料的弹性模量为0.5E、E、1.5E时，分别计算立管的涡激振动响应下的疲劳损伤，计算结果如图11及表3所示。

由图11可以看出，立管的疲劳损伤对于弹性模量的变化较为敏感。随弹性模量的增加，立管疲劳损伤峰值呈上升趋势，由图可以看出，随弹性模量的增加，立管激发出的模态数明显增加，这是由于弹性模量的改变直接导致立管惯性矩以及固有频率的变化，进而改变激发的模态数目，高阶模态的响应下，立管产生更高水平的弯曲应力循环导致疲劳损伤的升高。

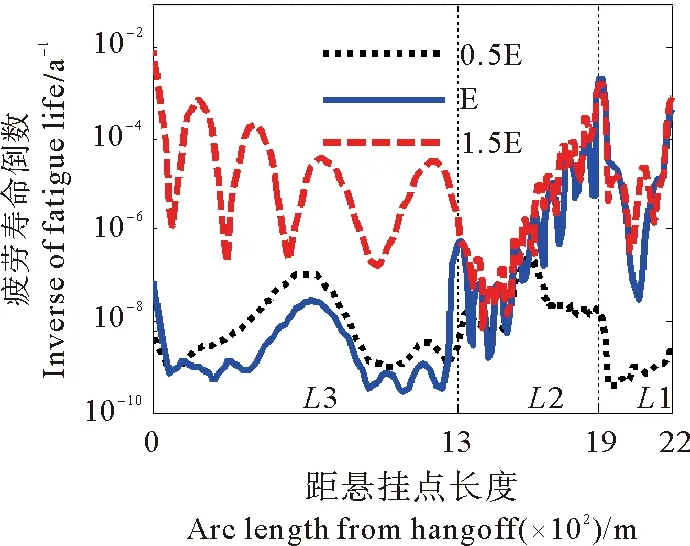
图11 不同弹性模量立管疲劳损伤对比Fig.11 Comparison of fatigue damage of riser with different elastic modulus

由图11以及表3可以看出，关键点疲劳寿命以及最小疲劳寿命随弹性模量的增加出现不同程度的降低；随着弹性模量的增加，最小疲劳寿命点由浮子段末端向悬挂点移动；因此实际工程根据实际情况选择合适的立管材料尤为关键，建议选取低弹性模量高应力的材料[29]。

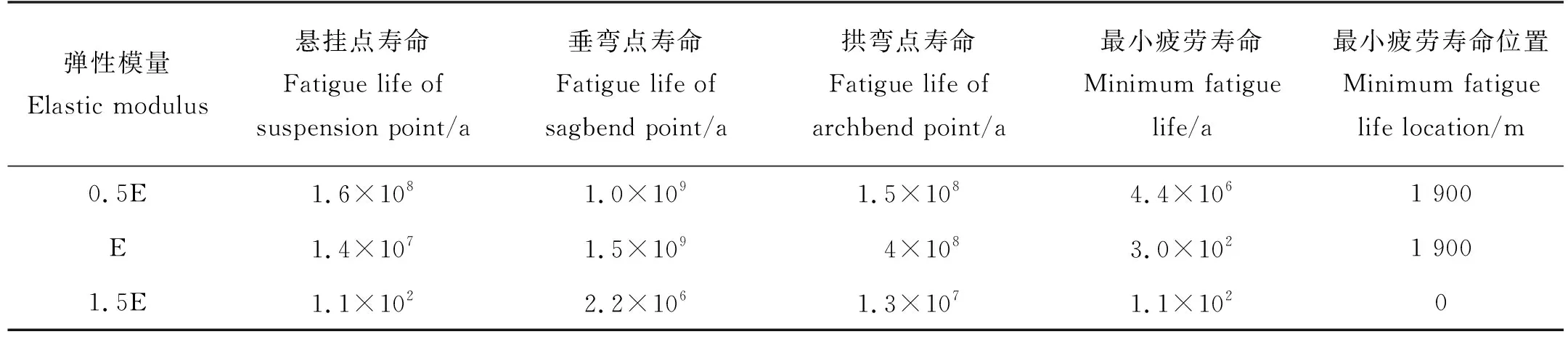
表3 不同弹性模量立管疲劳寿命Table 3 Fatigue life of riser with different elastic modulus

2.5 海流速度参数敏感性分析

保持立管其他参数不变，当海流速度v=0.80、0.825、0.85 m/s时，分别计算立管的涡激振动响应下的疲劳损伤，计算结果如图12及表4所示。

立管整体疲劳损伤随外部流速增大而升高，这与文献[30]中对于悬链线形立管的疲劳损伤结果一致。由图12可以看出流速越高立管被激发出来的模态越高，高模态下立管弯曲应力以及循环计数频率会增加，进而导致立管疲劳损伤程度整体升高；下降段、浮子段疲劳损伤对于海流速度的敏感度高于悬垂段；由表4看出，高流速导致关键点处疲劳寿命以及最小疲劳寿命出现大幅度下降，最小疲劳寿命位置始终位于浮子段末端。

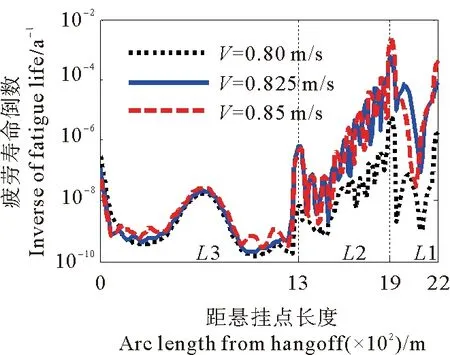
图12 不同海流速度立管疲劳损伤对比Fig.12 Comparison of fatigue damage of riser with different current velocities

表4 不同海流速度立管疲劳寿命Table 4 Fatigue life of riser with different current velocities

2.6 波浪高度的参数敏感性分析

本文利用莫里森方程计算波浪水动力荷载，同时考虑波浪作用下立管的动力响应以及海流作用下的横流向涡激振动响应，计算陡波立管的疲劳损伤。保持立管其他参数不变，当波高H=0、5、10 m时，分别计算立管的疲劳损伤，计算结果如图13及表5所示。

由图13可以看出，浮子段、下降段表现出较低的敏感度，而悬垂段对于波浪高度的变化敏高度极高，并且随着波高的增大，悬挂点附近疲劳损伤急剧升高，这主要是因为悬垂段靠近海面，波浪对悬垂段的直接作用使悬挂点附近应力循环水平急剧升高，导致疲劳寿命急剧下降；由表5可以看出，立管的各关键点处疲劳寿命以及最小疲劳寿命随波高的增加均出现了不同程度的降低；由于波浪的作用，最小疲劳寿命点由浮子段末端转移至位于悬挂点附近并保持位置不变。因此在实际工程设计中应慎重考虑立管所处海域的波浪情况，并在悬挂点附近采取必要的消波措施。

表5 不同波浪高度立管疲劳寿命Table 5 Fatigue life of riser with different wave heights

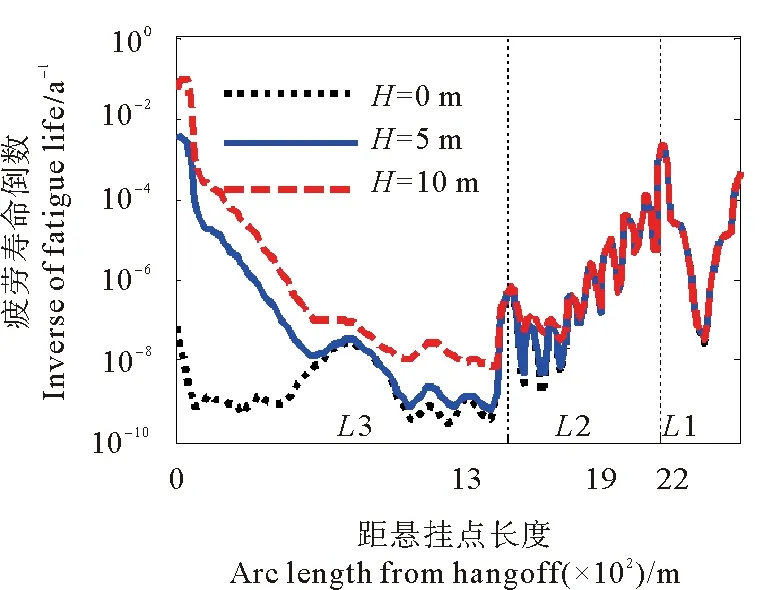
图13 不同波浪高度立管疲劳损伤对比Fig.13 Comparison of fatigue damage of riser with different wave heights

3 结论

本文基于柔性杆理论和尾流振子模型，综合使用S-N曲线法、雨流计数法与Palmgren-Miner线性累积损伤理论编写程序对陡波形立管进行疲劳分析。分析了陡波形立管在不同浮子段长度、浮力因子、弹性模量、海流速度、波浪高度下涡激振动疲劳损伤的变化规律，得到如下结论：

(1)陡波形立管的疲劳损伤沿轴线方向呈振荡性质；一般情况下，浮子段疲劳损伤水平最高，除此之外，立管浮子段首末两端、边界末端区域由于存在应力集中现象，疲劳损伤均处于较高的水平；疲劳寿命最小位置主要位于悬挂点和浮子段末端，实际工程中应对这些关键节点附近采取恰当的抑振措施。

(2)立管疲劳损伤随浮子段长度的增加呈现上升趋势，实际工程中增加浮子段长度降低悬挂点张力的同时应考虑该参数对于疲劳损伤的显著影响。

(3)浮力因子的增加会导致立管疲劳损伤整体下降，悬垂段本征频率主要由张力控制，因此对该参数敏感度较高，增加浮力因子会较大程度减小该段的张力以及疲劳损伤程度。

(4)弹性模量的增加会导致疲劳损伤升高；在立管的设计中应选择合适的立管材料来改善立管的疲劳损伤，建议选取低弹性模量高应力材料。

(5)海流速度和波浪高度的增加都会导致立管疲劳损伤急剧升高。海流速度增加使立管激发出更高阶的模态，导致整体疲劳损伤的升高；由于波浪直接作用于悬垂段，悬挂点附近疲劳损伤随波高增加急剧极高，因此在立管设计过程中应充分考虑陡波形立管所处海域的实际情况，并在悬挂点附近需采取必要的消波措施。