基于开裂安全系数的新增泄水洞与正洞合理间距研究＊

曹 渊，陈贤丰，张国伟，齐 军，李德武△

（1.中国铁路兰州局集团有限公司定西工务段，甘肃 定西 743000；2.兰州交通大学土木工程学院，甘肃 兰州 730070）

由于受修建时设计规范和施工标准的限制，我国许多既有铁路隧道在营运后不同程度地存在各种病害[1]。水是引起铁路隧道诸多病害的根本诱因，新增泄水洞出现很多既有隧道渗漏水整治方案中，对于泄水洞开挖或者其他近邻隧道合理间距也逐渐成为诸多学者关注的课题。其中王伟等[2]在有限元软件基础上结合监测结果，验证双线隧道间距建议值的合理性；刘路[3]考虑隧道与立交相邻的影响因素，基于宏观+微观数学概率理论研究某公路隧道与立交的最小间距；宋伟超等[4]提出隧道合理间距以相近隧道塑性应变区发生贯穿时的间距为准，并借助有限元软件加以辅证其可行性；赵志辉[5]建立计算模型结合机械效能确定泄水洞和隧道正洞的位置分布。

以上研究主要集中在对大断面、机械施工邻近铁路隧道的合理间距进行分析，而对于运营线路新增小断面泄水隧洞的项目的合理间距研究相对较少。本研究依托松树湾隧道新增泄水隧洞工程段，利用Midas GTS NX 建立泄水隧洞-隧道结构模型，对陇海线松树湾隧道修建泄水洞施工过程进行数值模拟研究，分析泄水洞施工对正洞的位移及应力响应的影响，在此基础上讨论泄水洞距正洞不同距离对隧道断面的受力变形影响程度大小，根据分析结果合理优化设计方案，确定对正洞影响最小的泄水洞开挖距离。

1 工程概况

松树湾隧道（k1588+836）全长2 224.3 m，海拔2 000 m，宽4.9 m，高6.55 m。隧址综合特点表现为富含水，土体的稳定性极差，岩土层理裂隙发达，不规则分布，属于铁路隧道中最软弱、稳定性最差的不良地层。其中松树湾隧道K1588+413-414 前后渗漏水问题发展较快。经由多方协商确定该段治理方案为增设泄水洞，可有效减轻该区段引排水系统系统排水压力，但相比较于一般泄水洞本项目泄水洞属于小断面洞，并且全过程采用人工手持风镐凿除围岩，相比较爆破施工对围岩的扰动性更小，由此需要进行泄水洞开挖面与正洞截面合理距离的研究。

2 计算模型建立

2.1 模型材料参数

松树湾隧道（1960 年建成）因其年代久远，受修建时勘探技术和设计标准的限制，其有效资料残存尚不完善，本次计算根据参考文献[6-7]关于既有松树湾隧道复线的新松树湾隧道设计施工资料，结合TB 10003—2016《铁路隧道设计规范》确定模型材料物理参数（见表1）。Midas GTS NX 在数值模拟中岩土材料多采用换算指标剪切模量G 与体积模量K，其换算关系见式（1）、式（2）。隧道二衬结构采用梁单元模拟。由于混凝土腐蚀、老化等原因，所以用模拟既有隧道衬砌时，衬砌混凝土厚度按折减10 cm 计算。泄水洞支护参数：C30 混凝土，支护厚度30 cm。

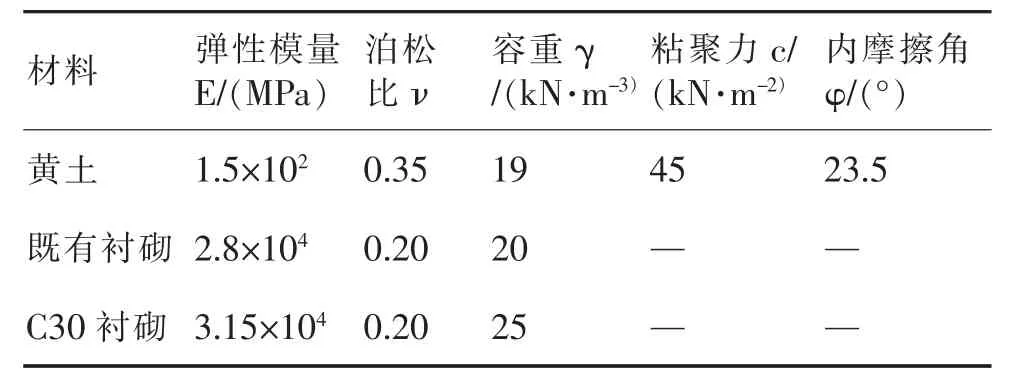
表1 模型材料物理力学参数表

式（1）、式（2）中：G-剪切模量；K-体积模量；ν-泊松比；E-弹性模量。

2.2 边界条件确定

对于模型边界条件的设定通常包括两部分，即位移边界和应力边界。本次模拟采用位移边界条件，即：模型沿着隧道开挖方向前后面（x=-25 m；x=25 m）固定其纵向位移；模型水平方向左右面（z=-30 m；z=40 m）固定其水平位移；模型竖直方向下表面（y=-20 m）固定其竖向位移；模型竖直方向上表面为自由面，对其不进行约束，可以自由变形。

2.3 有限元模型及施工工序

关于隧道数值模拟中，模型边界范围取值可根据圣维南原理，根据隧道跨度、高度选取：隧道的净高为6.55 m，净宽为4.9 m；左侧取距隧道左侧最大跨37.55 m 的边界、右侧取距隧道右侧最大跨37.55 m的边界，上侧边界距拱顶50 m，下侧边界距隧道仰拱低30.45 m。正洞选用全断面开挖法，开挖后一次施作二衬；泄水洞采用全断面一次开挖，开挖后对拱顶、边墙和底部施作混凝土支护。数值模拟中隧道开挖的应力释放系数取0.5。本次分析建立有限元模型及泄水洞位置如图1 所示。

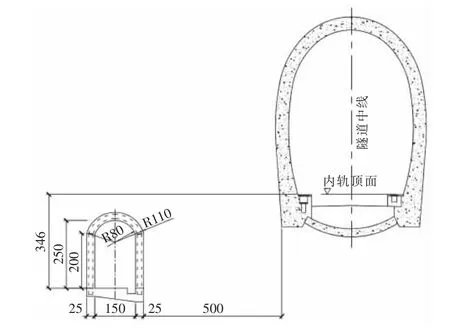
图1 隧道正洞与泄水洞位置示意图

3 泄水隧洞开挖面与正洞截面合理间距分析

日本《接近隧道施工对策指南》规定一般将近邻隧道相互影响范围分为3 个区间，其中无影响范围为间距>2.5 D。借鉴该规定，本项目新增泄水洞（d=2.5 m、D=3.1 m），推断泄水洞开挖面与正洞最安全的间距范围为6.25～7.75 m。但相比较于一般泄水隧洞本项目泄水洞属于小断面隧洞，并且全过程采用人工手持风镐凿除围岩，相比较爆破施工对围岩的扰动性更小，因此，本次研究将间距梯度依次取为4 m、5 m、6 m，讨论泄水隧洞开挖面与正洞截面合理距离。

3.1 泄水隧洞开挖对既有衬砌结构轴向应力响应分析

在既有铁路隧道单侧开挖泄水隧洞时，必然引起原有围岩应力发生变化，随之会导致围岩发生应力重分布，对于既有松树湾隧道素混凝土衬砌结构表现为其受力模式的不同。以此通过对其最不利应力响应进行分析有一定的必要性。针对三个不同间距工况，取泄水隧洞开挖前后的衬砌应力响应变化如图2 所示，对不同间距下既有隧道衬砌结构进行稳定性分析。

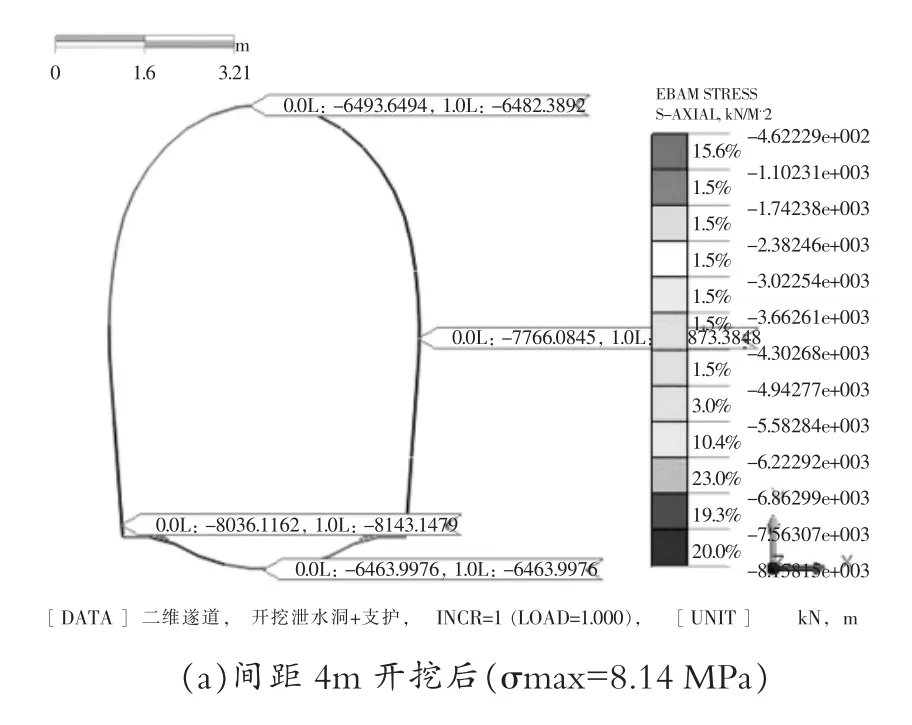
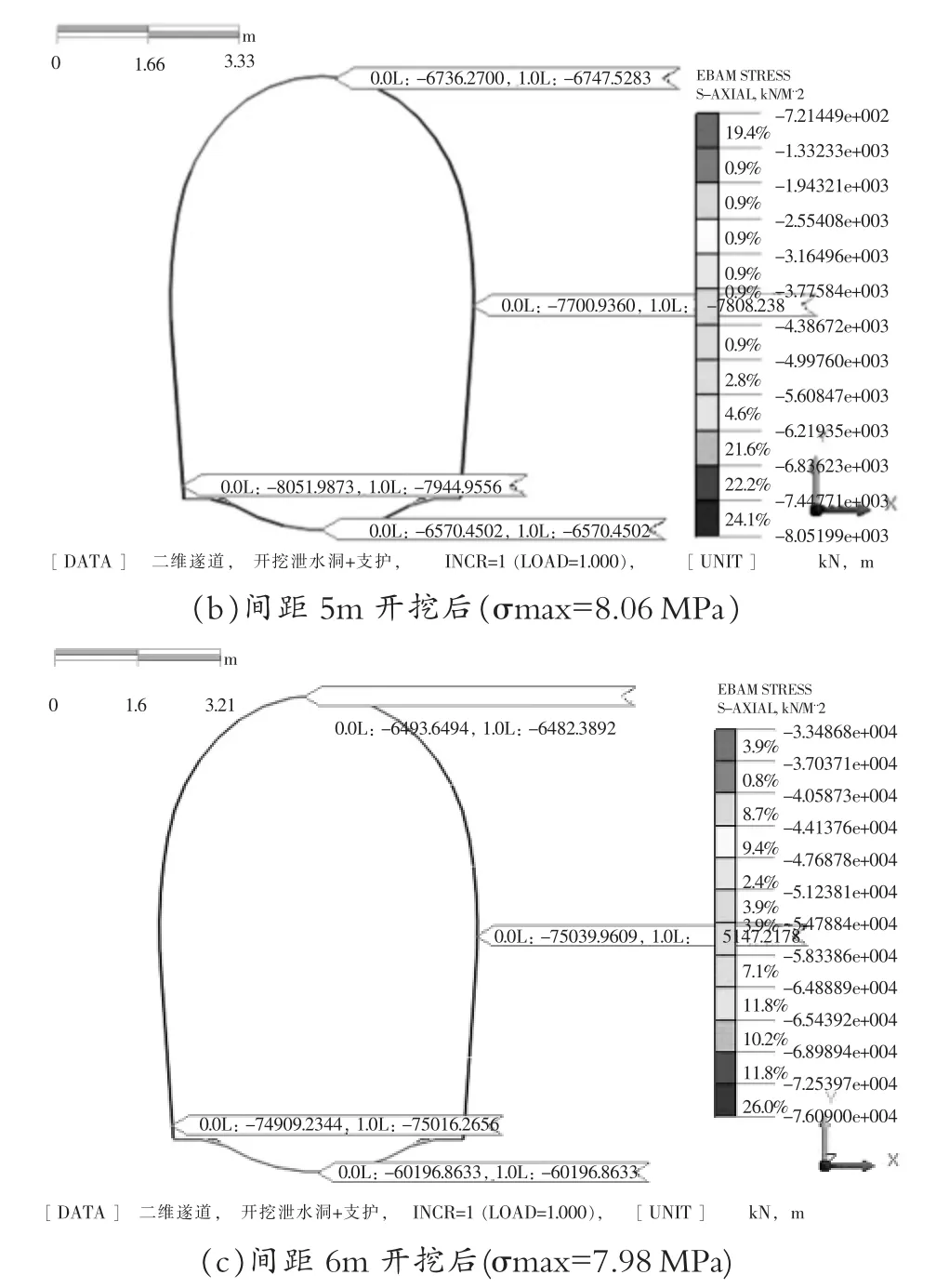
图2 不同间距下既有隧道衬砌结构最大轴向应力云图

由图2 可知：①从应力集中区域的分布来看，随着泄水隧洞开挖面与正洞间距越大，既有隧道衬砌的最大轴向应力响应整体呈现下降的趋势。但拱顶、仰拱的应力响应出现小幅度增大的趋势，究其原因是在间距较小时，其塑性区范围与正洞开挖后衬砌边墙侧塑性区发生重合，既有衬砌出现不利的影响相应，随着间距的增大，二者塑性区范围重合区域逐渐减少，泄水洞施工对原衬砌结构影响逐渐减小，但随着两者塑性区的分离，等价于整体塑性区面积增大，四周围岩的松胀位移变大，垂直于开挖面方向的围岩应力变化较大，因而既有隧道衬砌拱顶、仰拱出现小幅的应力增长现象；②无论间距怎么变化，最大应力响应表现为对既有隧道近邻开挖一侧的衬砌结构影响最大，这与王起才等[8]研究结论相符。且最大应力均出现在靠近开挖侧的拱脚；③从应力集中区域最大轴向应力值来考虑，只有间距为6 m 时原衬砌结构最大轴应力值为7.98 MPa，其量值上处于可控范围内。

3.2 既有隧道开裂安全系数分析

当泄水洞开挖面距隧道6 m 时，既有铁路隧道衬砌结构的轴向应力响应符合强度标准要求，但松树湾隧道既有衬砌结构为素混凝土脆性材料，多年运营条件下其内部可能存在裂隙，当泄水隧洞开挖引起的受力模式改变时，衬砌表面易产生开裂病害；而且Griffith 认为材料内部裂缝在裂缝尖端容易产生应力集中，当超过材料抗拉强度时，引发裂缝扩展，加剧材料的裂损降低其结构承载力。因此，需要对既有衬砌结构是否发生开裂进行判定。

本次采用文献[9]中定义的开裂安全系数Crack Factor（CF）作为混凝土开裂判定系数。此开裂安全系数由Griffith 准则变形得到，当CF＜1 时无开裂，当CF＞1 时，衬砌结构混凝土开裂。其计算公式为：

当

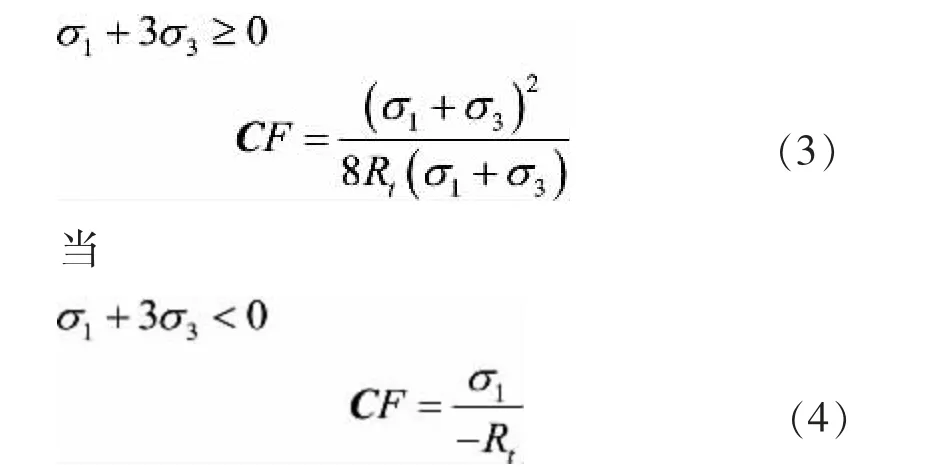
式（3）、式（4）中：R 为混凝土的极限抗拉强度；σ1，σ3为最大、最小主应力。

既有隧道二次衬砌为C20 素混凝土，根据TB 10003—2016《铁路隧道设计规范》，其极限抗拉强度Rt=1.7 MPa。采用式（3）和式（4）计算出既有隧道二衬结构的安全系数如图3 所示。

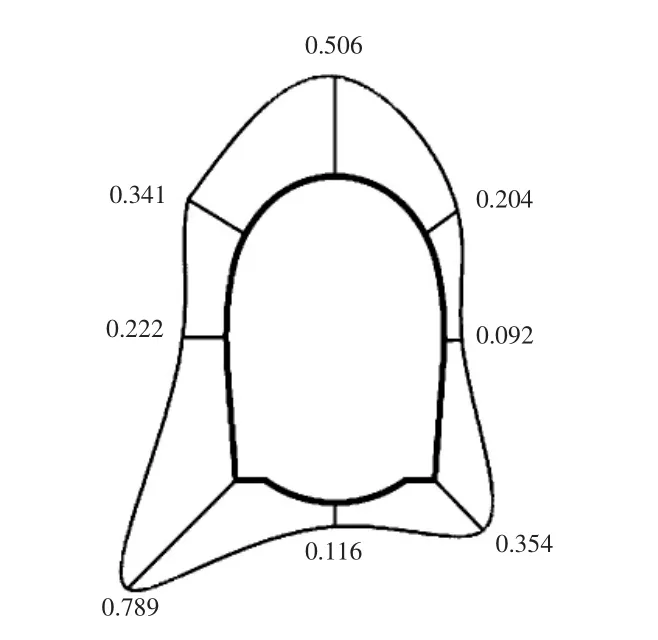
图3 既有衬砌截面开裂系数分布图

由图3 可知：①泄水洞开挖面距隧道6 m 时，既有隧洞衬砌截面CFmax=0.789<1，表明当间距为6 m时泄水洞开挖不会引起既有衬砌表面开裂；②在靠近开挖侧的拱脚、拱顶位置开裂安全系数较大，表明在既有隧道单侧开挖泄水隧洞，引发围岩应力的重新调整形成新的应力状态过程会改变既有隧道的衬砌结构受力模式，造成一定的应力集中现象，影响衬砌结构的强度稳定性。

3.3 泄水隧洞开挖对既有衬砌结构稳定性影响分析

图4、图5 为间距6 m 时泄水隧洞开挖下既有隧道的位移云图及塑性区分布情况，对泄水隧洞开挖面与隧道间距6 m 工况进行进一步结构稳定性讨论。

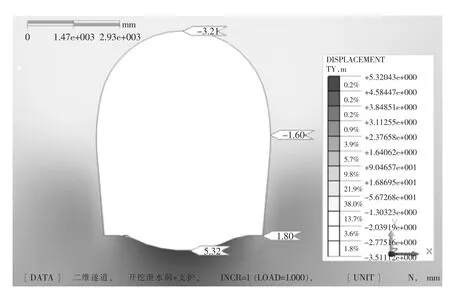
图4 泄水洞开挖下既有衬砌结构位移云图

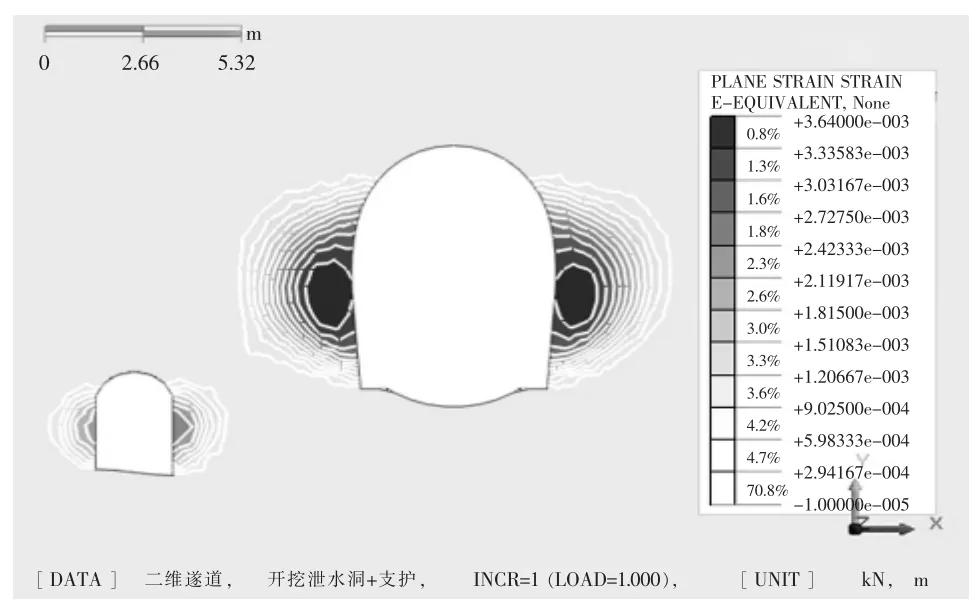
图5 泄水洞施工后塑性区分布图

由图4 可以看出，泄水洞开挖下，既有隧道的变形趋势为拱顶沉降、仰拱隆起的发展趋势，但是其最大变形位移出现在仰拱为5.3 mm，变形在规定范围之内；由图5 可以看出，泄水洞开挖后塑性区未与既有隧道围岩塑性区相交，不会形成塑性区贯通而造成结构失稳的情况。

4 结论

既有隧道单侧新增泄水洞工程，泄水洞开挖面与正洞截面的间距直接影响既有隧道的运营稳定性，对不同间距工况下泄水洞开挖对正洞的影响效应进行研究，选取合理的间隔。结论如下：

（1）泄水洞施工下既有衬砌应力响应规律：既有隧道衬砌的最大轴向应力响应随二者间距增大整体呈现下降的趋势；最大应力响应表现为对既有隧道近邻开挖一侧的衬砌结构影响最大；当只有间距为6 m 时原衬砌结构应力响应满足强度稳定性；

（2）当泄水洞开挖面距隧道6 m 时，既有隧洞衬砌截面的最大开裂安全系数<1，不会引起既有衬砌表明开裂；

（3）当泄水洞开挖面距隧道6 m 时，泄水洞施工下既有隧道的变形趋势及塑性区分布符合稳定性规定；

（4）综上，从既有衬砌结构强度及稳定性影响效应来看，间距为6 m 时符合相关规范规定。后考虑到泄水洞潜孔施工作业空间的限制，其仰角不宜过大，最终选定设计泄水洞与正统连接通道长6.85 m（如图6 所示）。但仍需注意对既有隧道衬砌靠近开挖侧的拱脚、拱顶位置进行及时的监控量测，密切关注其应力及变形情况，当出现响应异常值时需要采用必要的加固措施。

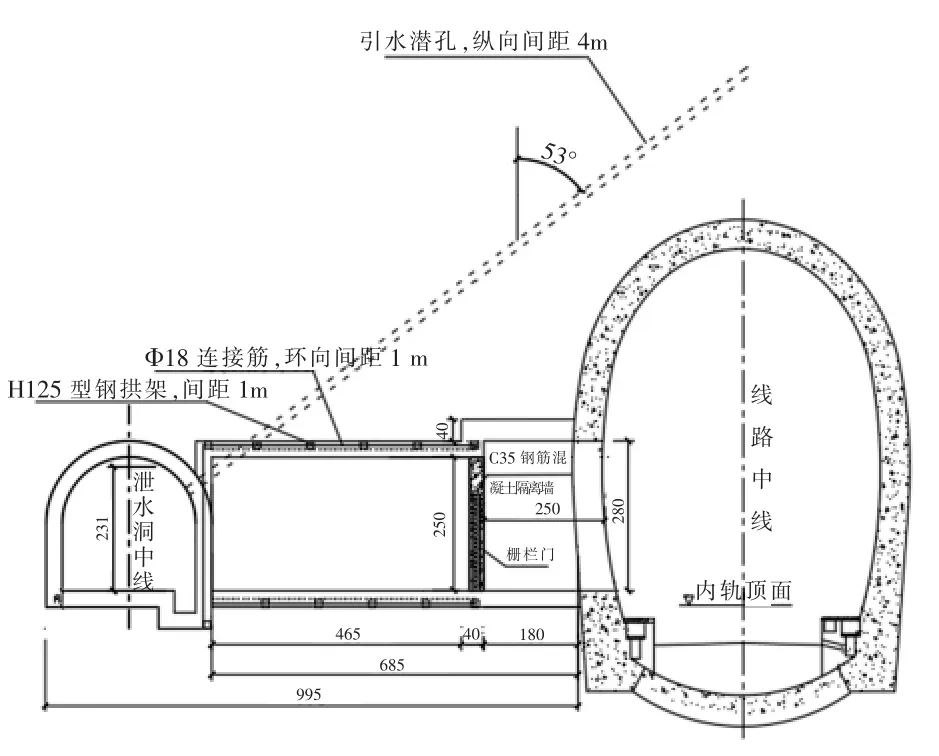
图6 泄水洞连接通道剖面图