基于多目标遗传算法的实验目标车底盘结构优化

黄 维，刘惟伊，刘志恩，卢炽华

（1.武汉理工大学现代汽车零部件技术湖北省重点实验室，湖北武汉430070；2.武汉理工大学汽车零部件技术湖北省协同创新中心，湖北武汉430070）

智能汽车已成为世界车辆工程领域的研究热点和汽车工业增长的新动力，是汽车技术发展的必然趋势。智能汽车的驾驶辅助系统在探测到可能会发生的危险时，可直接进行刹车等操作，以提升驾驶的安全性。在测试智能汽车驾驶辅助系统的避让和自动刹车等性能时，若使用普通车辆作为道路障碍车，则存在较大的碰撞风险。因此，需使用特殊道路障碍车来开展碰撞试验。实验目标车作为针对碰撞试验而设计的特殊道路障碍车，由集成了动力、控制及转向等系统的金属底盘和可重复拼装的软泡沫车身组成，且金属底盘高度一般不超过130 mm。当智能汽车（试验车）因算法不完善或控制不及时等而与行驶的实验目标车发生碰撞时，实验目标车的软泡沫车身会迅速分散，试验车从实验目标车的金属底盘上方碾过，可避免在碰撞试验过程中试验车和实验目标车的损坏。

某款实验目标车底盘的壳体结构如图1所示，主要由盖板、框架、裙边和底板构成。由于底盘总高度较低且布置空间十分紧凑，其内部的电动机等动力元件以及电池等供能元件的功率和容量均受到了限制。同时，底盘的总质量将极大地影响实验目标车的行驶性能（如最大加速度、最大速度和制动性能等），因此需对底盘结构进行轻量化设计。此外，实验目标车底盘内部元件与底盘壳体的间隙较小，为避免实验目标车在被高速行驶的试验车碰撞碾压时其底盘内部元件受到盖板的冲击，需对底盘盖板对舱内的侵入度进行分析。综上，对实验目标车底盘结构进行轻量化设计时必须考虑其抗碾压性能。

基于此，笔者拟利用显式非线性有限元法对实验目标车金属底盘的抗碾压性能进行分析，并基于多目标遗传算法对金属底盘进行结构设计和优化，在保证其抗碾压性能的前提下实现低成本和轻量化，由此获得一种综合考虑离散变量和多种性能的实验目标车底盘结构优化方法。

图1 实验目标车底盘壳体结构Fig.1 Experiment target vehicle chassis shell structure

1 实验目标车底盘结构性能分析

1.1 底盘有限元模型建立

利用HyperMesh软件构建实验目标车底盘有限元模型。根据底盘的三维几何模型，简化密封条、螺栓等对底盘抗碾压性能影响很小的结构，并将底盘中的主要功能部件简化为质量块。为了在提高分析速度的同时保持较高的计算精度，采用尺寸为4～10 mm 的单元对底盘三维模型进行网格划分。实验目标车底盘有限元模型如图2所示。

图2 实验目标车底盘有限元模型Fig.2 Finite element model of experimental target vehicle chassis

实验目标车底盘壳体主要钣金件所用材料的性能参数如表1所示。

1.2 底盘有限元模型有效性评估

为了保证所建立的实验目标车底盘有限元模型的有效性，通过模态分析和静力学分析进行验证。基于OptiStruct求解器，对自由模态、重力下垂和下压力三种工况下的底盘有限元模型进行分析。自由模态分析用于评估底盘有限元模型中各部件的连接关系，通过分析得到底盘前4阶自由模态的固有频率和振型，如图3所示。由图3可知：底盘的一阶自由模态固有频率为34.14 Hz，二阶自由模态振型为整体弯曲模态，底盘刚度满足设计要求；底盘中盖板、框架、裙边和底板的连接处均不存在局部模态，说明构建的各连接关系约束基本正确。对1g重力载荷下的底盘进行静力学分析，获得重力作用下底盘自然下垂的变形量。结果显示：1g重力载荷下，底盘的最小离地间隙为18.90 mm，与实测值18.00 mm接近。在底盘盖板顶部施加10 kN下压力，通过静力学分析得到下压力加载节点处的变形量为4.71 mm，与实测值5.00 mm基本一致。综上可知，所建立的底盘有限元模型有效且可靠，可用于实验目标车底盘碰撞碾压过程仿真分析。

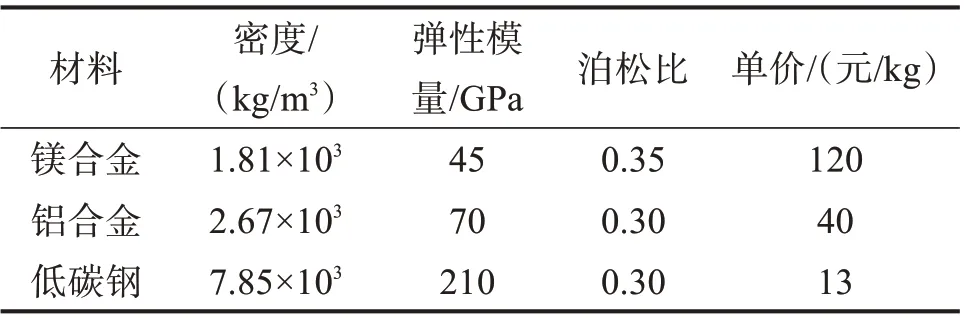
表1 实验目标车底盘壳体材料的性能参数Table 1 Performance parameters of chassis shell material of experimental target vehicle

1.3 底盘抗碾压性能分析及优化空间确定

根据车辆制造企业提出的最大碾压车速设计要求，基于RADⅠOSS 求解器，对相对速度为80 km/h（22.22 m/s）的试验车和实验目标车进行碰撞碾压过程仿真分析。需要说明的是，由于代表智能汽车的试验车的有限元模型比较复杂，故本文采用课题组之前建立的轿车模型代替。仿真分析工况包括10%，30%，50%，70%，90%的正面碾压工况以及10%，20%，40%，60%，80%，90%的侧面碾压工况。图4所示为50%正面碾压和40%侧面碾压工况下试验车与实验目标车底盘的位置关系。为了简化分析，设定试验车的速度为80 km/h，实验目标车固定不动，其底盘底板约束于地面。分析时考虑重力的影响。

对11个碾压工况下实验目标车底盘的抗碾压性能进行有限元仿真分析。根据仿真结果，选取底盘前、后盖板以及侧盖板上位移变形最大的点，以及与舱内零部件间隙小于10 mm的点，共计12个点。定义这些点为侵入度测量点，并将侵入度测量点的位移变形量作为底盘抗碾压性能的评价指标：位移变形量越小表明底盘的抗碾压性能越好。图5所示为12个侵入度测量点在盖板上的位置分布。表2所示为各侵入度测量点所对应的危险零部件、最大变形位移及其与危险零部件的最小间隙。

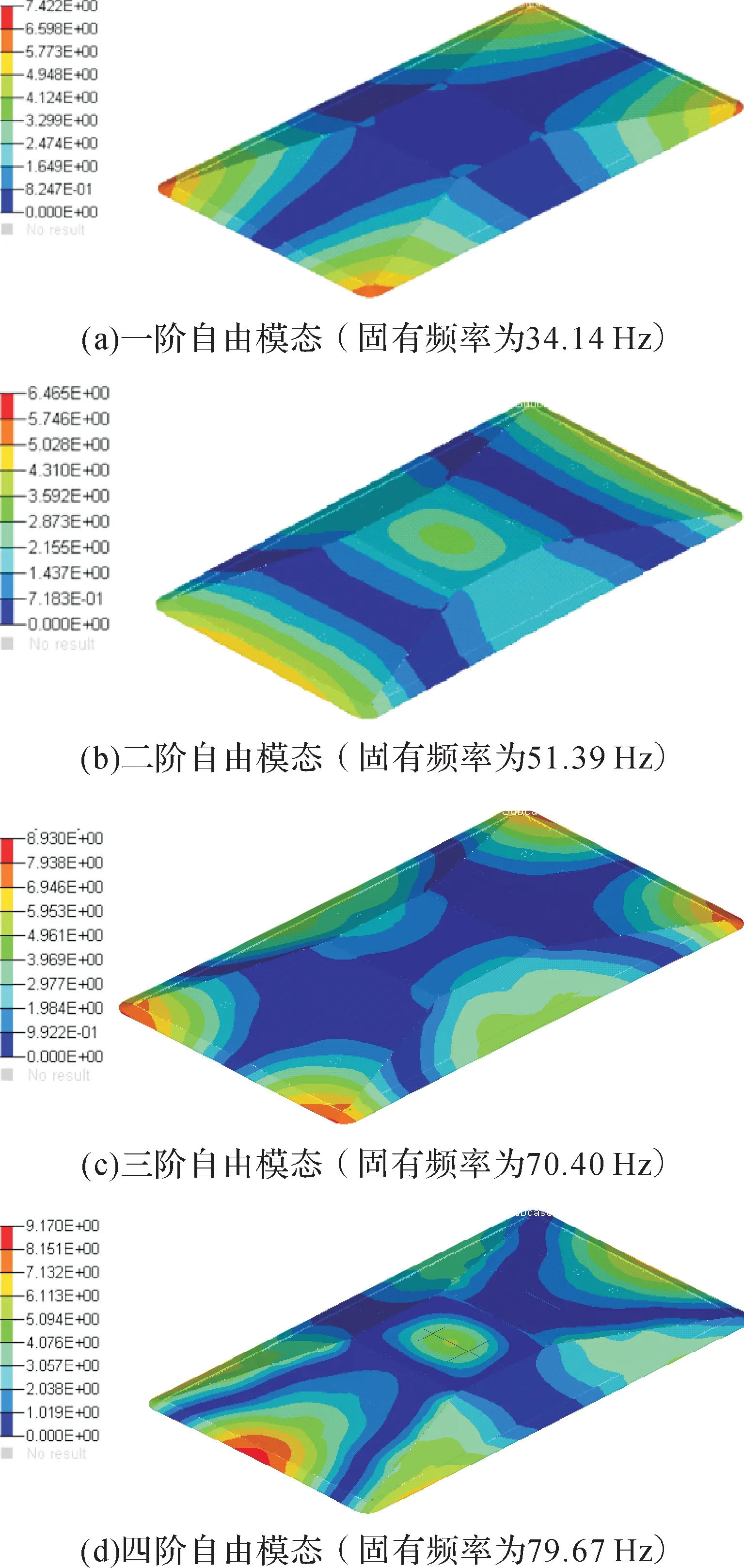
图3 实验目标车底盘前4阶自由模态振型Fig.3 Shape of first four free modes of experimental target vehicle chassis

图4 不同碾压工况下试验车与实验目标车底盘的位置关系Fig.4 Positional relationship between test vehicle and experimental target vehicle chassis under different rolling conditions

由表2可以看出，不同侵入度测量点的最大变形位移及其与危险零部件的最小间隙各不相同。在对底盘结构进行优化时，应注意这些侵入度测量点对抗碾压性能的要求。

图5 侵入度测量点的位置分布示意图Fig.5 Schematic diagram of location distribution of intrusion measurement points

表2 各侵入度测量点的最大变形位移及其与危险零部件的最小间隙Table 2 Maximum deformation displacement of each intrusion measurement point and minimum gap between it and dangerous part

2 实验目标车底盘结构优化模型

2.1 优化变量的确定

实验目标车底盘壳体结构是一类几乎全部由钣金件组成的特殊框架结构，钣金件的厚度及材料都具有较大的优化空间。如图6所示，根据对称性，选取9个厚度变量，定义为t1、t2、…、t9，均为连续变量；与厚度变量相对应，选取9个材料变量，定义为m1、m2、…、m9，均为离散变量，材料的选择范围为镁合金、铝合金和低碳钢。

2.2 优化目标及约束条件的确定

在对实验目标车底盘进行优化设计时，以底盘总材料成本最低为优化目标1，以底盘总质量最小为优化目标2，将满足抗碾压性能要求作为约束条件。

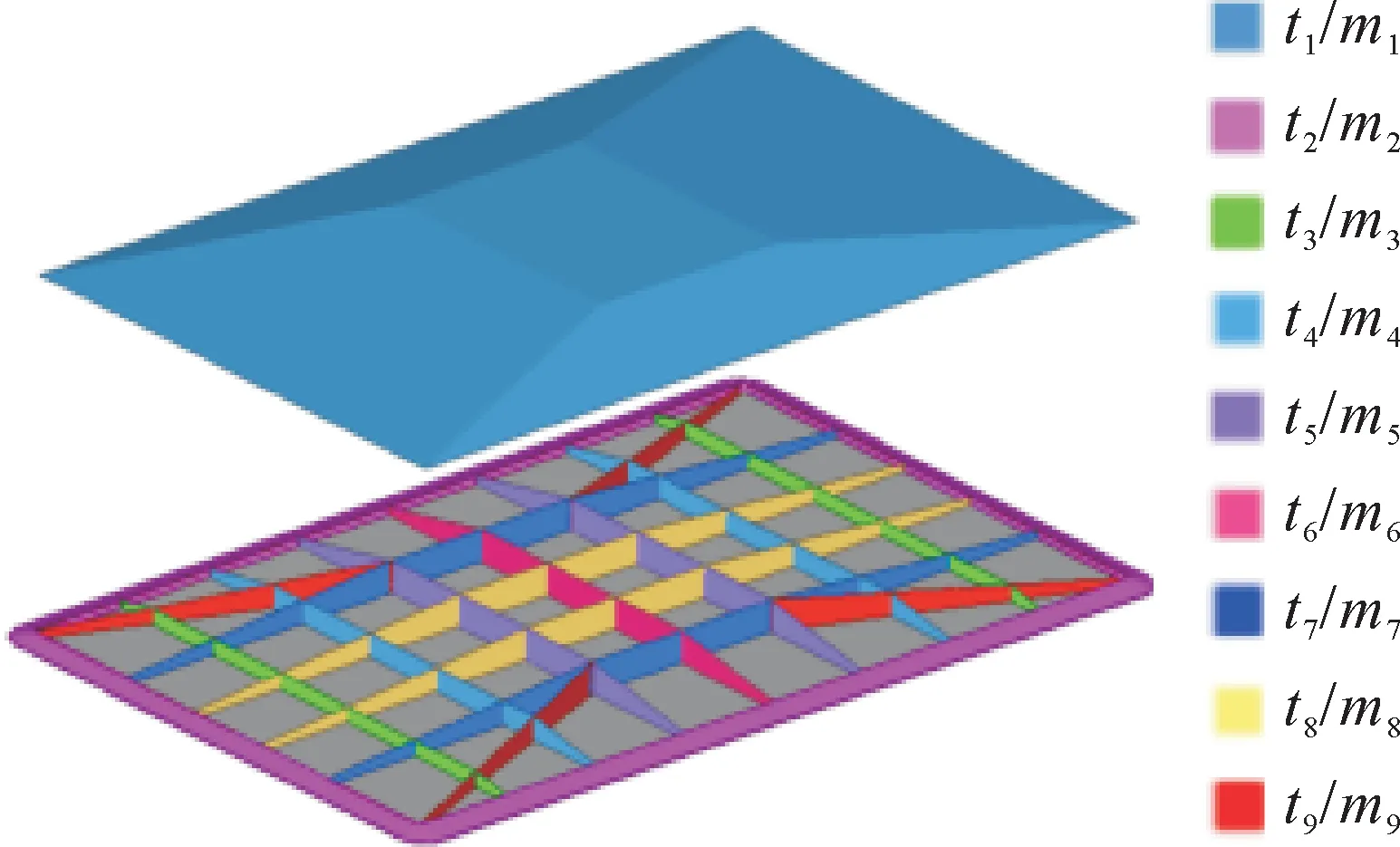
图6 实验目标车底盘结构优化变量Fig.6 Optimization variables of experimental target vehicle chassis structure

底盘总材料成本包括管理成本和制造成本，其中材料成本通常占制造成本的60%以上［3］，因此本文仅将占比最大的材料成本作为优化目标。在计算材料成本时，需获取不同材料零部件的质量，而各零部件的质量又取决于其面积、材料密度及厚度。本文通过构建外部函数的方式来计算底盘的质量和材料成本。实验目标车底盘总质量及材料成本的计算式如下：

式中：M 为实验目标车底盘总质量；C为实验目标车底盘总成本；Mi为第i个零部件的质量；ρi为第i个零部件材料的密度；ti为第i个零部件的厚度；ci为第i个零部件的面积；pi为第i个零部件材料的单价。

通过上述公式计算得到实验目标车底盘的总质量为171 kg，初始材料成本为6 193元。

将实验目标车底盘上12个侵入度测量点的最大变形位移分别设为约束条件1，2，…，12。为保证底盘舱内各零部件的安全性，设各侵入度测量点最大变形位移的约束值上限为其与危险零部件最小间隙的70%；同时，为保证实验目标车底盘的其他结构性能（一阶自由模态固有频率、下垂刚度和下压刚度）不大幅度降低，设各侵入度测量点最大变形位移的约束值下限不小于初始值的90%。

2.3 优化算法和近似模型的确定

钣金件厚度和材料的多目标优化求解存在一定困难：既存在离散变量，又存在连续变量，导致优化过程的非线性程度较高，且在寻优过程中易陷入局部最优［4-5］。由于非线性优化问题没有解析解，使得求解过程的耗时很长，且多个目标的同时优化会令求解难度进一步提高［6-7］。目前，常用的多目标优化算法包括全局响应面法和多目标遗传算法等。针对复杂的非线性优化问题，多目标遗传算法具有独特的优势［8］。

但是，遗传算法的收敛对种群规模和迭代次数有较高的要求，且运算量一般较大［9］。因此，结合有限元仿真的多目标遗传算法一般会通过构建近似模型来节省优化时间和提高优化效率［10-12］。对于较复杂、非线性程度较高的优化问题，克里金方法具有较强的适应性［13-14］。因此，本文采用克里金函数来构建实验目标车底盘结构优化问题的近似模型。

在传统多目标遗传算法中，当近似模型的预测精度较低时，通常采用均匀增加样本点等方式对近似模型进行修正。在基于有限元仿真的遗传优化问题中，均匀增加样本点会直接增加仿真迭代次数，这对基于有限元仿真的多目标遗传优化非常不利。因此，找到一种合适的策略来合理选择样本点，是节约计算成本、提高优化效率和减小误差的关键［6］。

基于此，本文提出了一种基于局部放大法的遗传算法，即在完成一次遗传优化后，若近似模型的预测精度不满足要求，则将优化变量的取值范围缩小至最优点附近，重新选取试验设计（design of experiments，DOE）样本点，生成新的近似模型后再进行优化。基于局部放大法的遗传优化流程如图7 所示。该方法的优点是：在每一步优化后，可在样本点不大幅度增加的基础上提高近似模型的预测精度，大大减轻了仿真计算的压力。

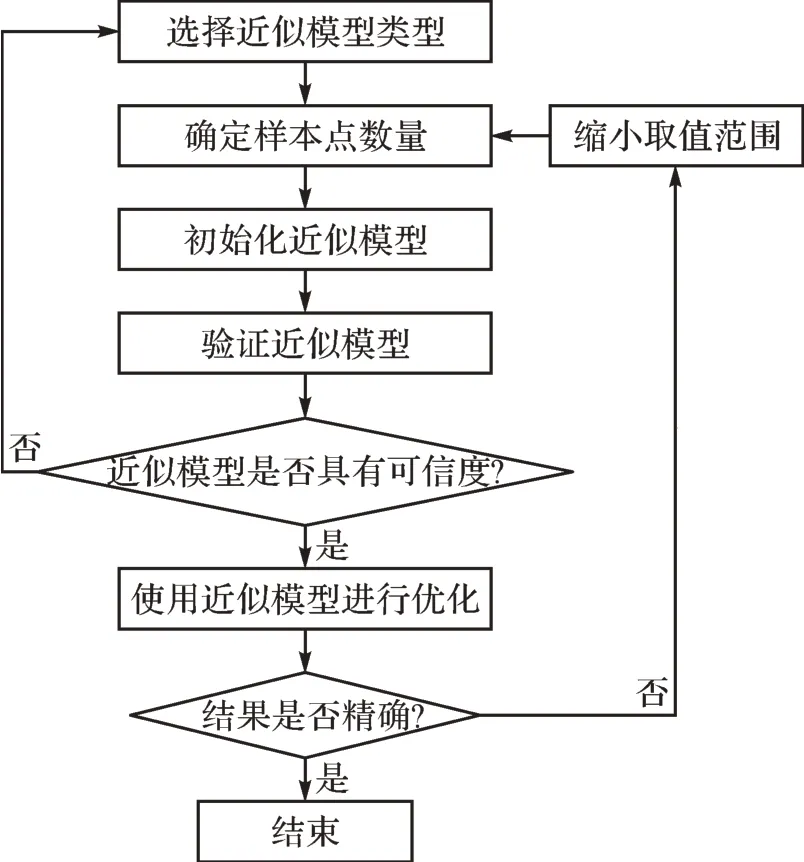
图7 基于局部放大法的遗传优化流程Fig.7 Genetic optimization flow based on local amplification method

3 实验目标车底盘结构的多目标遗传优化

3.1 初次优化

通过上文分析结果可知，实验目标车底盘结构存在较大的优化空间。基于实验目标车底盘抗碾压性能的分析结果，设定较宽的厚度取值范围：t1、t2、…、t9的取值范围均为2～10 mm。

基于哈默斯利DOE方法确定样本点数量。基于本文优化变量的数量为18 个，取380 个样本点。将样本点导入RADⅠOSS求解器进行求解，初步获得用于实验目标车底盘结构优化的克里金近似模型。

基于获得的初始克里金近似模型，采用多目标遗传算法对实验目标车底盘结构进行初次优化，设定种群规模为84个，最少迭代次数为25次，最多迭代次数为50次。经过34次迭代后，种群规模达到了5 124个，此时优化计算达到收敛。初次优化得到的实验目标车底盘结构设计方案的可行解及最优解如图8所示。

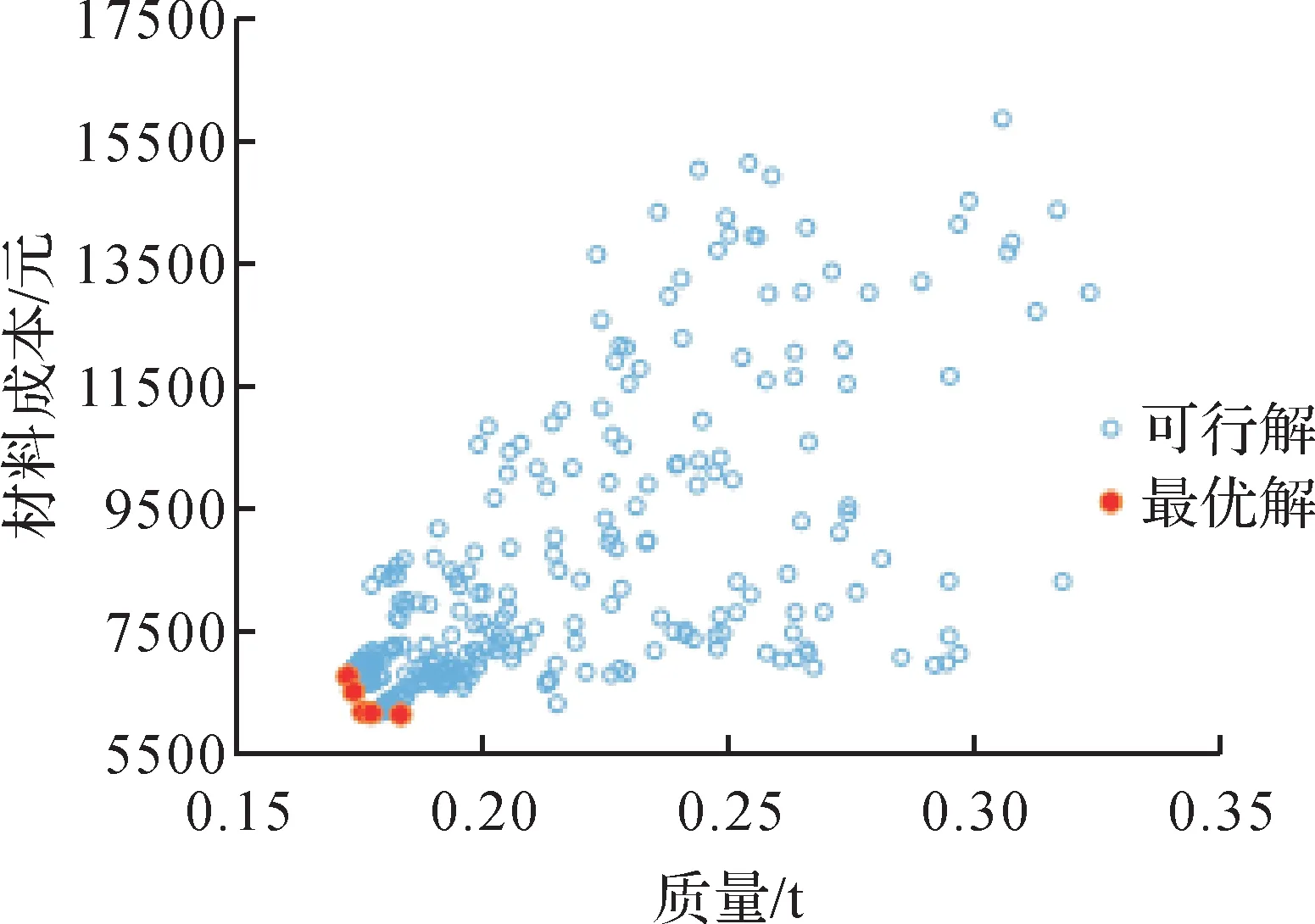
图8 初次优化得到的实验目标车底盘结构设计方案的可行解及最优解Fig.8 Feasible solutions and optimal solutions of experimental target vehicle chassis structure design scheme obtained by initial optimization

由图8 可以看出，初次优化得到了5 组最优解；随着优化计算的迭代，可行解出现了区域集中的现象，最优解趋于离散。这是因为材料变量为离散变量，不同的材料组合使得最优解之间存在较大的差异。

将初次优化得到的5组最优解导入RADⅠOSS和OptiStruct求解器进行计算，获得不同最优解对应的实验目标车底盘结构性能（各侵入度测量点的最大变形位移、一阶自由模态固有频率、下垂刚度和下压刚度）、质量和材料成本的真实值，并与近似值进行比较，求得两者的相对误差，结果如表3所示。

由表3 可以看出，对于初次优化得到的设计方案，实验目标车底盘质量的相对误差较大，平均达到了17.7%，最高达到了28.6%。因此，认为初步建立的近似模型的预测精度不满足要求，需进行修正。

3.2 再次优化

基于局部放大法，重新确定样本点数量，再次生成新的克里金近似模型。设置与初次优化相同的条件，对实验目标实验车底盘结构再次进行优化。经过47 次迭代后，种群规模达到7 193 个，优化计算达到收敛。再次优化得到的实验目标车底盘结构设计方案的可行解和最优解如图9所示。

表3 初次优化后实验目标车底盘结构性能、质量和材料成本的相对误差Table 3 Relative error of structural performance, quality and material cost of experimental target vehicle chassis after initial optimization %

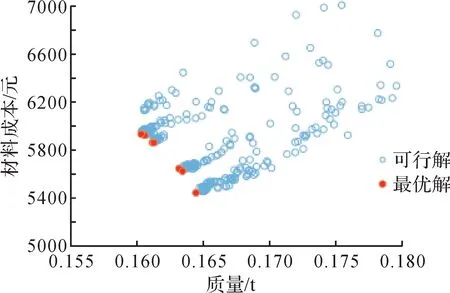
图9 再次优化得到的实验目标车底盘结构设计方案的可行解和最优解Fig.9 Feasible solutions and optimal solutions of experimental target vehicle chassis structure design scheme obtained by re-optimization

由图9 可以看出，再次优化后得到了7 组最优解，且优化解的离散程度有所提高。将7个最优解导入RADⅠOSS 和OptiStruct 求解器进行计算，获得不同最优解对应的实验目标车底盘结构性能、质量和材料成本的真实值，并与近似值进行对比，求得两者的相对误差，结果如表4所示。

对比表3和表4可知，采用基于局部放大法的多目标遗传算法进行优化后，近似模型最优解的相对误差大幅度减小，平均误差均在10%以下。由此可以认为，经过局部放大后的克里金近似模型具有较高的预测精度，优化结果准确，因此可将基于该近似模型获得的设计方案作为优化方案。

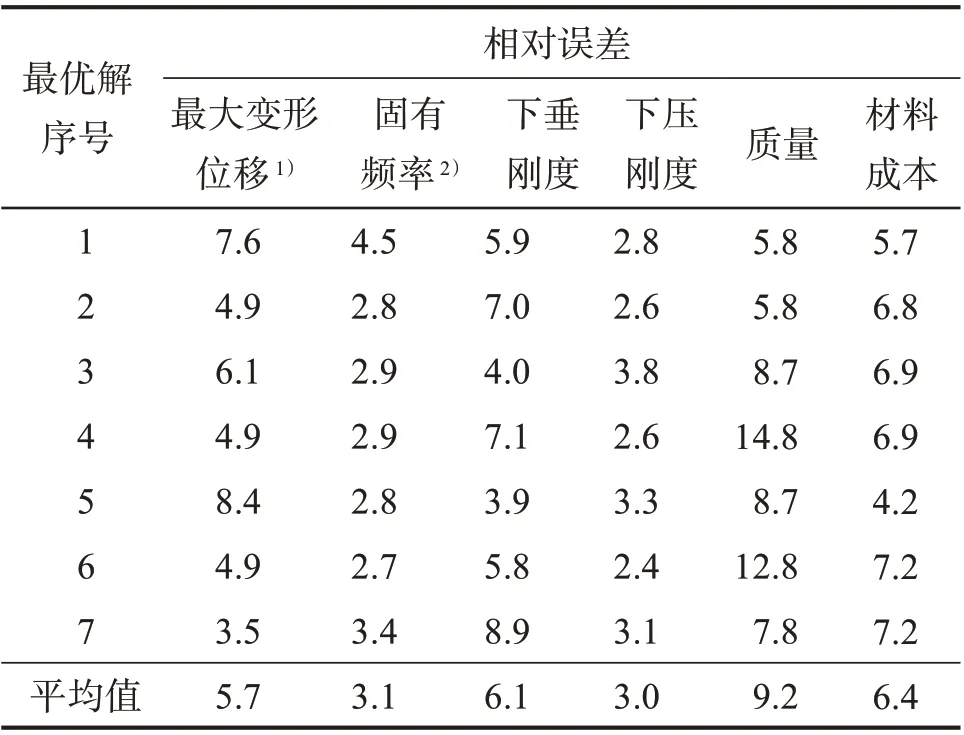
表4 再次优化后实验目标车底盘结构性能、质量和材料成本的相对误差Table 4 Relative error of structural performance, quality and material cost of experimental target vehicle chassis after re-optimization %

3.3 最优方案确定

将采用基于局部放大法的多目标遗传算法得到的7组实验目标车底盘结构优化方案与初始方案（优化前底盘结构的设计方案）进行对比，结果如图10所示。由图10可知，相较于初始方案，7组优化方案均同时实现了质量减小和材料成本下降的目标。结合材料变量和厚度变量的约束条件可得：方案2，3基本重合，方案4，5基本重合，方案6，7基本重合，可分别视为相同方案。

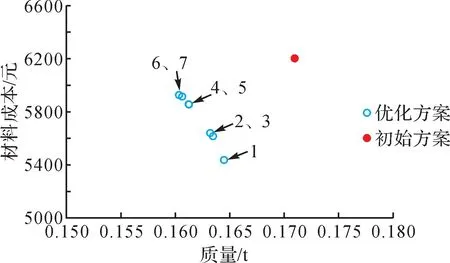
图10 实验目标车底盘结构优化方案与初始方案对比Fig.10 Comparison of optimized scheme and initial scheme of experimental target vehicle chassis structure

将方案1作为方案A，在方案2，3中任选一组作为方案B，在方案4，5中任选一组作为方案C，在方案6，7中任选一组作为方案D。4组优化方案对应的实验目标车底盘结构的设计变量如表5所示。

将4组最优方案对应的设计变量导入RADⅠOSS和OptiStruct求解器进行计算，得到对应的实验目标车底盘的结构性能、质量和材料成本，结果如表6所示。

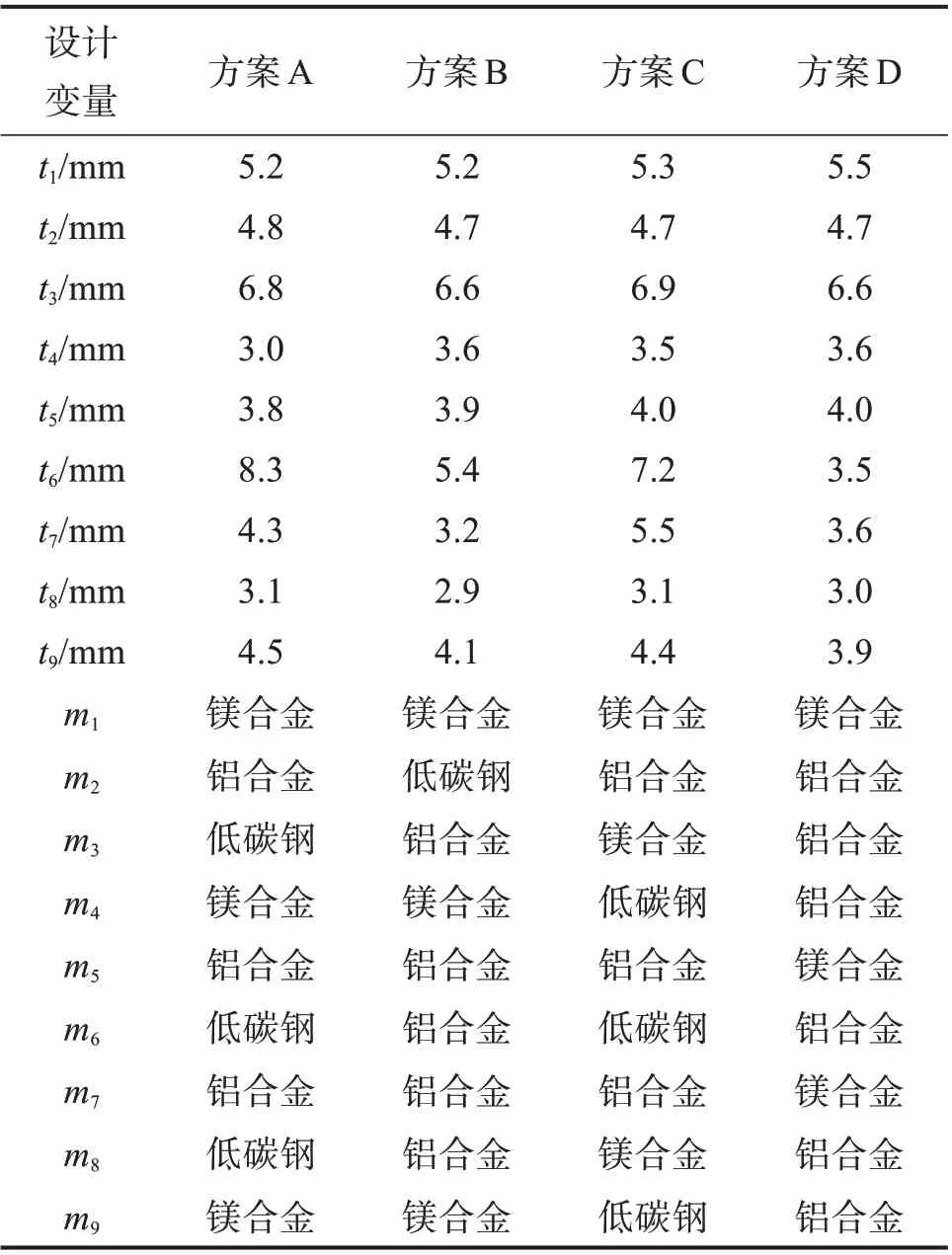
表5 不同优化方案对应的实验目标车底盘结构设计变量Table 5 Design variables of experimental target vehicle chassis structure corresponding to different optimization schemes

由表6可知，通过基于局部放大法的多目标遗传优化，4组实验目标车底盘结构优化方案在满足抗碾压性能及其他结构性能要求的基础上，分别实现了以下目标。

方案A：材料成本下降755 元，下降了12.2%；质量减小7 kg，减小了4.1%。

方案B：材料成本下降574元，下降了9.3%；质量减小8 kg，减小了4.7%。

方案C：材料成本下降338元，下降了5.4%，质量减小9 kg，减小了5.3%。

方案D：材料成本下降265元，下降了4.3%，质量减小11 kg，减小了6.4%。

由此可知，4 组优化方案的优化效果各不相同。从经济角度考虑，方案A的材料成本最低，是经济性最佳的设计方案；从轻量化角度来看，方案D的质量最小，是轻量化效果最佳的设计方案。

将经济性最佳的方案A作为参照，可对比得出：对于方案B，底盘质量每减小1 kg需要增加181元；对于方案C，底盘质量每减小1 kg需要增加208.5元；对于方案D，底盘质量每减小1 kg需要增加122.5元。从减小质量、提高成本这一角度来看，方案D具有较好的优化效果。

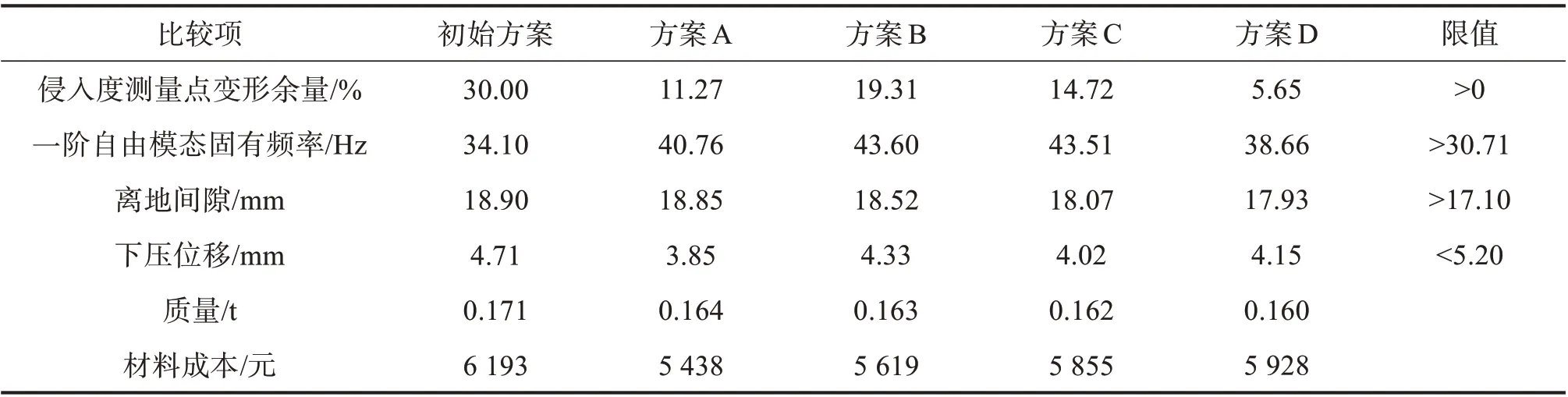
表6 优化前后实验目标车底盘的结构性能、质量和材料成本对比Table 6 Comparison of structural performance, quality and material cost of experimental target vehicle chassis before and after optimization

将方案D作为参照，可对比得出：对于方案A，底盘每下降100元成本需要增大0.810 kg；对于方案B，底盘每下降100元成本需要增大0.970 kg；对于方案C，底盘每下降100 元成本需要增大2.739 kg。从降低成本、增大质量这一角度来看，方案A具有较好的优化效果。

在企业实际生产和应用过程中，经济性往往是重要考虑因素之一［15］，其直接影响产品的竞争力和企业的经济效益。但结构的质量会影响产品的动力性能（如加速度、最大速度和制动减速度等）和燃料（电池）成本［16］，这对于实验目标车尤为重要。从上文对比可得，方案D对应的实验目标车底盘的轻量化效果最佳，因此选用方案D 作为最终的底盘结构设计方案。

4 结 论

本文对实验目标车底盘结构的多目标优化问题进行了研究，得到了以下结果。

1）采用基于局部放大法的多目标遗传算法解决实验目标车优化问题时可以减少样本点数量和仿真运算量，以及提高近似模型的预测精度，从而获得较好的优化结果。

2）设计的实验目标车底盘结构多目标优化流程综合考虑了底盘的各项性能以及设计方案的经济性和轻量化效果。结果表明结合碰撞碾压仿真结果与多目标遗传算法的优化设计流程具有适应性强、优化结果准确和多目标协同满足程度高的特点。

3）从经济性和轻量化等不同角度出发，对获得的优化方案进行性能评价，并结合优化结果和企业实际应用情况，确定了最终的实验目标车底盘结构设计方案。相较于初始方案，底盘结构材料成本下降了4.3%，质量减小了6.4%，同时实现了经济性和轻量化，且提升了实验目标车底盘的抗碾压性能。